Using genetic information to test causal relationships in cross-sectional data

Abstract

Cross-sectional data from twins contain information that can be used to derive a test of causality between traits. This test of directionality is based upon the fact that genetic relationships between family members conform to an established structural pattern. In this paper we examine several common methods for empirically testing causality as well as several genetic models that we build on for the Direction of Causation (DoC) model. We then discuss the mathematical components of the DoC model and highlight limitations of the model and potential solutions to these limitations. We conclude by presenting an example from the personality and politics literature that has begun to explore the question whether or not personality traits cause people to hold specific political attitudes.

1. Introduction

Causal relationships are of great interest to political scientists as they form the foundation for the theoretical structure for hypothesis-driven empirical research. While existing theoretical models typically imply causal relationships among the various constructs under investigation, the ability to test these causal relationships is relatively impoverished. Below we enumerate a Direction of Causation (DoC) model for testing causality between variables and compare the DoC model to various other methods that are commonly employed to assess causal structure. In order to clarify the explication and utility of the DoC model, throughout this paper we rely on an example that has recently become a hot topic in the political behavior literature: the causal relationship between personality traits and political attitudes (Gerber et al., 2010; Mondak et al., 2010; Verhulst et al., 2010; Verhulst et al., 2012).

2. Causality

Establishing causality is a very complex endeavor that has occupied philosophers and scientists for thousands of years (e.g., Aristotle, Bacon, Hume, and Kant). Some discussion of the meaning of causality is necessary when developing empirically based causal models, but broad discussions of causality and epistemology are beyond the scope of this article and are better presented in any number of relevant philosophical tomes (Pearl, 2009; Rubin, 1974). Rather, we aim to provide a cursory examination of directly relevant causality theory that envelops the current discussion of contemporary statistical methods.

The classic way of testing causality in the sciences is through experimentation. If subjects are randomly assigned values of a variable (i.e., randomly assigned to conditions) and there exists some relationship between that variable and a subsequently measured variable, then it logically follows that the first variable caused the second. It is for this reason that the first variable is typically referred to as the independent variable, while the second is dubbed the dependent variable. This relatively straightforward test of causation makes experimentation the gold standard against which other methods of disentangling causality are compared. However, this method is appropriate only when the hypothesized causal variable can be experimentally manipulated, which is extremely difficult when studying the personality traits and behavioral attitudes relevant to political science.

In the absence of experimental manipulation, applied researchers may take advantage of so-called quasi-experimental designs and collect multivariate and clustered data (i.e., data which are not independently and identically distributed). Cross-sectional (Baron and Kenny, 1986) and longitudinal mediation (Cole and Maxwell, 2003), cross-lagged panel designs (Campbell, 1963; Campbell and Stanley, 1963), and instrumental variable regression (Wright, 1928) are examples of methods where data are collected such that either sufficiently multivariate or clustered longitudinal observations allow for the comparison of models with different causal flow. While substantive arguments regarding causation in longitudinal data come from temporal precedence, the comparison of models with different causal directions (i.e., X causes Y or Y causes X) comes from the difference in expected cross-variable longitudinal relationships in different causal models. This feature is not unique to longitudinal data, and can be applied to other types of clustered data.

The method of testing causal relationships we advocate in this paper is the Direction of Causation (DoC) model. In short, the DoC model predicts different cross-twin cross-trait correlations depending on which direction causation flows in much the same way as cross-lagged panel studies or other longitudinal methods. Because the DoC model does not rely on random assignment to experimental conditions, it can be utilized in a broad set of research scenarios. Importantly, and in contrast with longitudinal models, even if the causal event occurred before measurement, the direction of causality would still be evident in the observed covariance structure and can therefore be captured by the DoC model. Accordingly, the DoC model has many advantages over other empirical methods and provides a very useful method of disentangling causal relationships between variables.

Our discussion of the DoC model proceeds in several stages. We first briefly review the basic univariate variance decomposition of twin data and a multivariate extension called the Cholesky decomposition. Building on these genetic models, we outline the basic mathematical components of the DoC model as well as some important limitations and potential solutions to these problems. Finally, we apply the DoC model to an example from the personality and politics literature that highlights its usefulness as a test of theoretical assumptions that are common in the political science literature.

2.1. The basics of twin and family studies

Twin and family studies are typically used to estimate the heritability of observed traits by comparing family members of varying genetic relatedness. This procedure commonly relies on monozygotic (Mz) and dizygotic (Dz) twins, but siblings, half-siblings, adopted siblings, or any other genetic relations can also be employed (see Neale and Cardon, 1992 or Medland and Hatemi, 2009 for a review).

A variety of models exist which capitalize on genetic relatedness within families to test for genetic variance of an observed trait or phenotype. Importantly, the use of family data requires several assumptions regarding the underlying relationships between relatives. Accordingly, empirical models that rely on twin and family data assume that Mz twins share all their genes while Dz twins and other first degree relatives share half of their genes, that people mate randomly with respect to the construct of interest, that the environments of Mz and Dz twins are equivalent, and that the fitted model accurately represents the data. As violations of these assumptions are dealt with in great detail elsewhere (Keller et al., 2009; Neale and Cardon, 1992), we do not discuss them here. These assumptions enable us to distinguish the impact of genetic and environmental effects on behavioral traits.

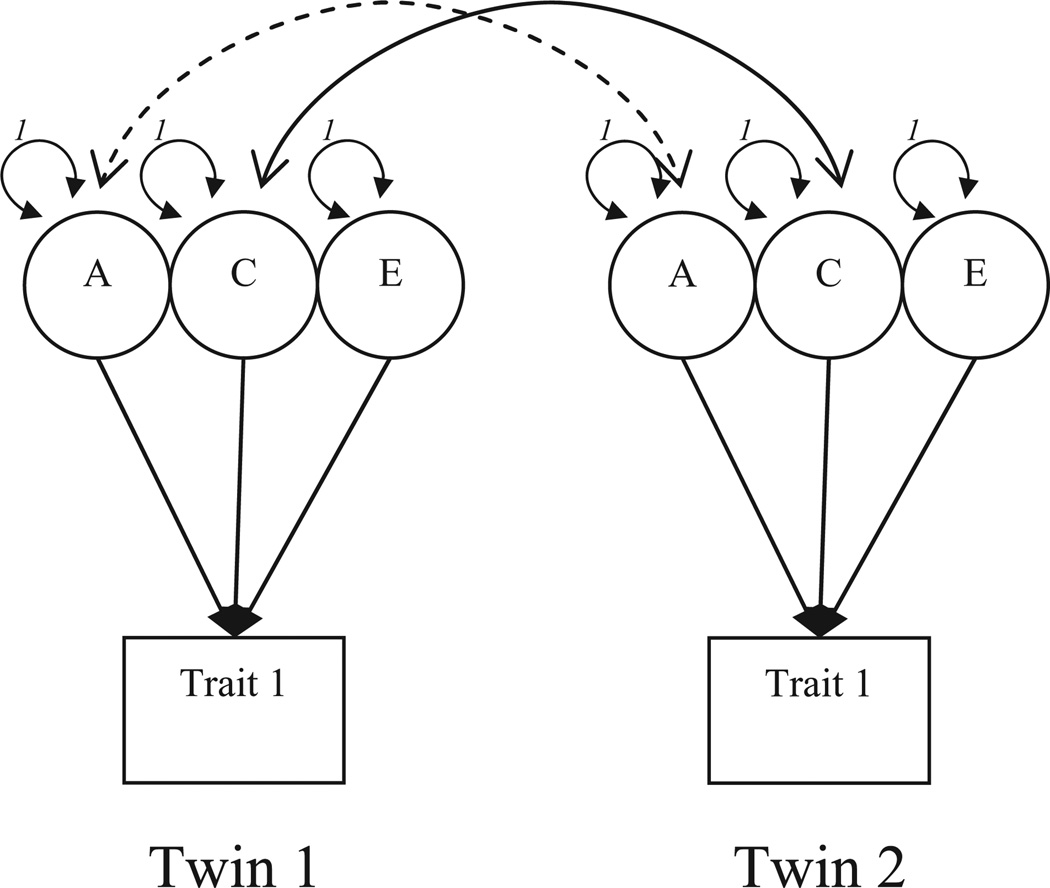
The most common method for estimating the genetic and environmental contributions to a construct is the classic twin (ACE) model which decomposes observed variance in a phenotype into three parts: Additive genetic, Common and unique Environmental variance components. In brief, the additive genetic variance component or the A factor captures the linear additive effect of genes on a construct, and is defined by a correlation of 0.5 in Dz twins and 1.0 in Mz twins. The common environmental variance component or the C factor represents environmental experiences shared by both twins, and is perfectly correlated across twins regardless of zygosity. Finally, the unique environment or E factor is uncorrelated across twins, representing the impact of the environment that is not shared by twins, including measurement error. The unique environment factor shows no correlation across twins regardless of zygosity (for a more detailed account of the ACE model see Neale and Cardon, 1992 or Medland and Hatemi, 2009). The path model for the classic twin (ACE) model is presented in Figure 1.

Figure 1. A path depiction of the basic univariate twin model.

Note: Circles denote unobserved or latent variables while rectangles denote observed or manifest variables. Single-headed arrows denote asymmetric or causal effects while double-headed arrows denote symmetric or covariances between variables. To simplify the presentation of the models, solid lines for the covariance between the shared environmental variance components indicate that the covariance is fixed at 1 for all types of twins while the dashed lines for the covariance between the additive genetic variance components indicate that the correlation is fixed at 1 for Mz twins and 0.5 for Dz twins.

2.2. Multivariate genetic analyses: The Cholesky decomposition

In most cases, however, we are interested in how two (or more) variables relate to each other. To this end, researchers in behavioral genetics have embraced the Cholesky decomposition because of its ability to adapt to the needs of family data. Simply put, the Cholesky decomposition is one method for taking a square root of a symmetric matrix. When a Cholesky matrix is multiplied by its transpose, the resulting matrix is symmetric and virtually always positive definite (see the appendix to Neale et al. (2005) for the analytical proof). As covariance and correlation matrices are symmetric by definition, the Cholesky decomposition is a very useful tool in the analyses of covariance structures, such as the twin model.

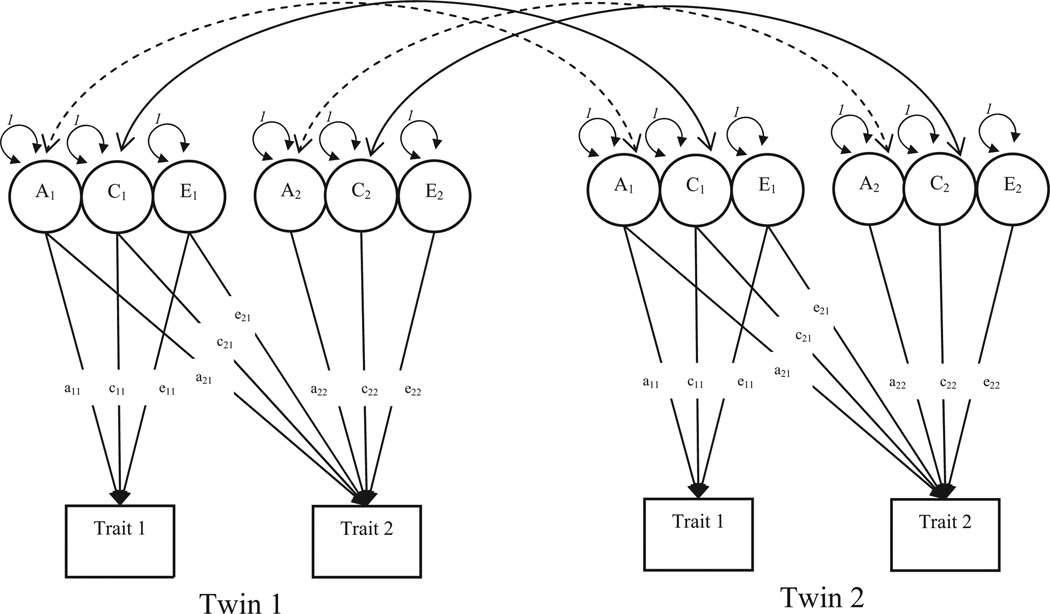
The fact that Cholesky decompositions are overwhelmingly positive definite makes it relatively simple to utilize them in statistics. Behavioral geneticists have capitalized on the utility of Cholesky matrices and use them as the basis of a variety of multivariate extensions of the univariate ACE model where they simultaneously decompose the variance of multiple traits into the separate variance components. For ease of explication, a path analytic depiction of a bivariate Cholesky decomposition can be found in Figure 2, though it should be kept in mind that the Cholesky decompositions can have as many variables as are relevant to the research question. As can be seen in Figure 2, the bivariate Cholesky decomposition estimates six latent factors (A1, C1, and E1, and A2, C2, and E2).¹ This estimation procedure assumes that the latent variables A1, C1, and E1 are the sole causes of Trait 1 as well as partial causes of Trait 2. The factors A2, C2, and E2 account for the residual variance in Trait 2 that is not shared with Trait 1.

Figure 2. The path specification of a bivariate Cholesky decomposition.

Note: Circles denote unobserved or latent variables while rectangles denote observed or manifest variables. Single-headed arrows denote asymmetric or causal effects while double-headed arrows denote symmetric or covariances between variables. To simplify the presentation of the models, solid lines for the covariance between the shared environmental variance components indicate that the covariance is fixed at 1 for all types of twins while the dashed lines for the covariance between the additive genetic variance components indicate that the correlation is fixed at 1 for Mz twins and 0.5 for Dz twins.

The algebraic formulation of the multivariate Cholesky decomposition of genetic models is equivalent to the univariate variance decomposition:

$${\mathbf{V}}_{\text{total}}={\mathbf{V}}_{\mathrm{a}}+{\mathbf{V}}_{\mathrm{c}}+{\mathbf{V}}_{\mathrm{e}}$$ (1)

where V_total is the full expected variance-covariance matrix and V_a, V_c, and V_e are the additive genetic, common environmental, and unique environmental variance-covariance matrices, respectively. In order to ensure that V_total is positive definite, V_a, V_c, and V_e can subsequently be decomposed into

$${\mathbf{V}}_{\mathrm{a}}=\mathbf{a}\mathbf{a}\prime$$ (2)

$${\mathbf{V}}_{\mathrm{c}}=\mathbf{c}\mathbf{c}\prime$$ (3)

$${\mathbf{V}}_{\mathrm{e}}=\mathbf{e}\mathbf{e}\prime$$ (4)

where a, c, and e are lower triangular Cholesky matrices that can be interpreted as path coefficients for the genetic and environmental paths (see Medland and Hatemi, 2009 for more detail). The expected covariance matrix is then compared with the observed covariance matrix by maximum likelihood.²

Although there are several benefits to the Choleksy decomposition, it provides relatively little insight into the causal structure between the constructs of interest. Instead, because the Cholesky decomposition is a fully saturated model analogous to a correlational model, correlation does not necessarily imply causation. To examine the causal structure that exists between two variables, it is necessary to estimate a model that empirically tests causation. The Cholesky decomposition serves a very useful purpose in the estimation of DoC models. Because the Cholesky decomposition estimates as many parameters as there are unique pieces of information in the data, it is typically used as the saturated model against which to compare hypothesis-driven models such as the DoC model, which we describe in detail in the next section.

2.3. Direction of causation model

The structure of the genetic relationships between Mz and Dz twins provides information that allows for the analysis of causal relationships. In contrast with traditional cross-sectional data analysis, the genetic information provided by the family structure allows the DoC model to utilize the cross-twin cross-trait covariance to determine the causal direction (Duffy and Martin, 1994; Gillespie et al., 2003; Heath et al., 1993; Neale and Cardon, 1992; Neale et al., 1994). The structural relationship between twins of varying levels of zygosity implies very specific predictions regarding the pattern of cross-twin cross-trait covariance.

Intuitively, if causation is unidirectional, then these cross-trait cross-twin covariances will be proportional to the genetic structure of the causal variable, with the proportion defined by the estimated regression parameter. If causation is bidirectional, then the cross-trait cross-twin covariances will be estimated as the combination of each trait’s genetic structures, with the regression coefficients defining this combination. If an external variable, or set of variables, drives the association between A and B, then the Cholesky will provide improved fit over the bidirectional model (Duffy and Martin, 1994; Heath et al., 1993; Neale and Cardon, 1992). Accordingly, the Cholesky decomposition suggests correlation rather than causation.

On a more detailed level, let us assume that we have two traits, A and B. Let us further assume that each trait has a unique pattern of genetic and environmental variance, where trait A has a substantial genetic component and no shared environmental component while trait B has a large shared environmental component and no additive genetic component (and both traits have unshared environmental variance). In this scenario, if A causes B, the cross-twin cross-trait covariance will be a function of the heritable component in Trait A and the within-person covariance between Trait A and Trait B. If B causes A, the cross-twin cross-trait covariance will be a function of the common environmental component in Trait A and the within-person covariance between Trait B and Trait A. Hence, the observed cross-twin cross-trait covariance is expected to be markedly different depending on whether A causes B or B causes A (for an extended mathematical proof see Duffy and Martin, 1994).

If the modes of transmission are equivalent for the two variables, then it will be impossible to determine the direction of causation as the cross-twin cross-trait covariances will predict the same covariance structure regardless of whether A causes B or the reverse. As such, the DoC model has the most power to determine causal effects if the modes of transmission for two variables are highly discrepant, whether due to the comparison of two different genetic structures (i.e., ACE for one trait, AE for another) or to varying values in two versions of the same model (i.e., ACE with large genetic variance for one trait, ACE with large common environmental variance for the another trait: Heath et al., 1993).

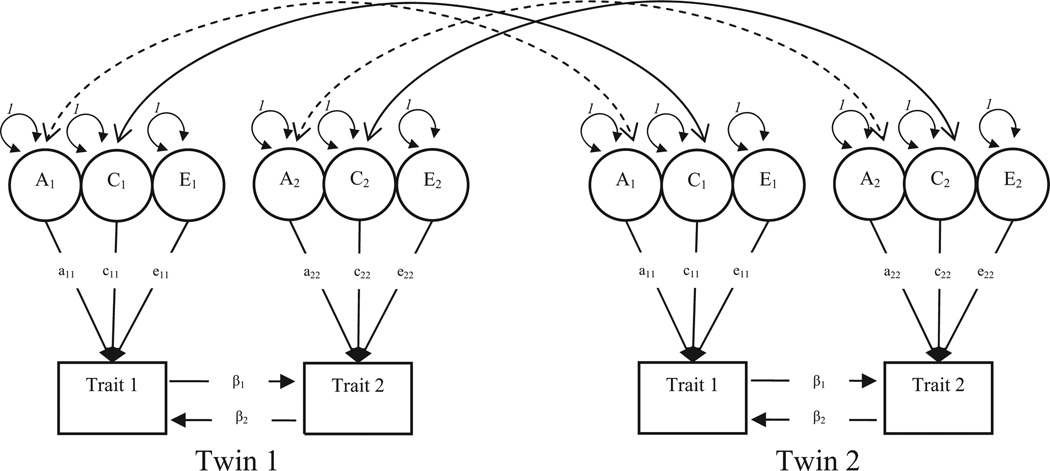
A visualization of the basic direction of causation model is presented in Figure 3.

Figure 3. Bivariate direction of causation model.

Note: Circles denote unobserved or latent variables while rectangles denote observed or manifest variables. Single-headed arrows denote asymmetric or causal effects while double-headed arrows denote symmetric or covariances between variables. To simplify the presentation of the models, solid lines for the covariance between the shared environmental variance components indicate that the covariance is fixed at 1 for all types of twins while the dashed lines for the covariance between the additive genetic variance components indicate that the correlation is fixed at 1 for Mz twins and 0.5 for Dz twins.

The DoC model allows the researcher to investigate five causal scenarios that may be the source of the association between two phenotypes. The first two possibilities are the unidirectional causal models where A is the cause of B, or where B is the cause of A. This scenario is what is implied by regression analyses where causality is simply assumed. The third possibility is that A and B are caused by an external factor or otherwise cannot be described via a simple causal structure. This may be represented by a Cholesky decomposition, as it has no implicit causal structure and represents a saturated model. The fourth possibility is reciprocal causation, where A and B have a non-recursive causal structure: A causes B at the same time that B causes A. The final model is one with no association between A and B.

Typically, these models are compared with likelihood ratio tests, in which one model is nested within another model.³ It is relatively clear that the unidirectional DoC models are nested within the non-recursive model and that the no-association model is nested within all of the other models (Cholesky decomposition, non-recursive, and both unidirectional models).

The nesting of the unidirectional models in the Cholesky decomposition is not intuitive, but these models are nested. For these models to be nested, it is necessary that the parameters of the smaller model be a subset of the parameters of the larger model, with the additional parameters removed through constraint either to zero or to the value of other parameters. A unidirectional version DoC model shown in Figure 3 is nested within the Cholesky in Figure 2, because the DoC model can be redrawn or reconceptualized. If the a₂₁, c₂₁ and e₂₁ paths in Figure 2 are constrained to be equal to the product of the regression weight β₁ and the within-trait genetic parameters a₁₁, c₁₁ and e₁₁, then the constrained Cholesky decomposition denotes the exact same model expectation as the unidirectional DoC model. While the path diagrams may look different, the same model may be drawn any number of ways and still be the same model. The expected means and covariances are identical, which is sufficient to denote that two models are equivalent and show the nesting of the unidirectional DoC model within the Cholesky.

Unlike all other comparisons among this set of models, the non-recursive DoC model is not nested within the Cholesky decomposition. Accordingly, while the likelihood ratio test to compare the non-recursive DoC and the Cholesky decomposition is typically performed, the validity of the test is impaired and not strictly correct. One alternative is to compare the non-recursive DoC model to the Cholesky decomposition using Akaike’s Information Criteria (AIC), which evaluate the fit of each model and penalizing the model fit for the inclusion of additional parameters. The model with the lowest AIC value is deemed the best fit to the data. While the AIC will be used to compare these two models, non-nested model comparison is inferior to the likelihood ratio test, which should be used for nested model comparisons when possible.

In accordance with the parsimony principle, the best model is the model that best captures the nuances of the data with the fewest free parameters. Specifically, if the fit of the restricted model is not significantly worse than the fit of the full model, the restricted model is judged to be the superior model. For example, if one of the unidirectional causal models does not fit significantly worse than the non-recursive model, then one would conclude that the unidirectional model better explains the data.

In these cases, the interpretation of the model is relatively straightforward. The parameters of the best model are interpreted. While it is likely that the most interesting parameter in the model will be the causal pathway, the genetic and environmental pathways may also be quite interesting as they allow for the assessment of the source of the causal variance. For example, if A causes B and the primary reduction in variance is localized in the genetic variance component, then it is possible to conclude that the genetic variance in A causes the genetic variance in B. If the reduction in variance is spread evenly across the genetic and environmental variance components then interpretation is more aligned with phenotypic causation. Furthermore, in unidirectional causation models it is possible to assess the reduction in variance accounted for by the causal variable, analogous to an R² statistic for each level of variance.

If all of the restricted models fit significantly worse than the Cholesky decomposition (the least parsimonious model), causality cannot be inferred. At that point it is necessary to conclude that the underlying structure is correlational, and is a function of shared genetic or environmental variance. Here, the parameters of the Cholesky become particularly relevant, as if the covariance is focused at either the genetic or environmental level it is possible to infer the primary source of the covariance, even if it is not causal. Specifically, if the common environmental covariance is not significant, this implies that the covariance between A and B is primarily a function of pleiotropic genetic effects (the covariance is a function one or more genes that contribute independently to both phenotypes). Alternatively, if the common environmental covariance is significant while if the genetic covariance is not, it should be concluded that environmental factors drive the covariance between traits.

2.4. Limitations of the DoC model and possible solutions

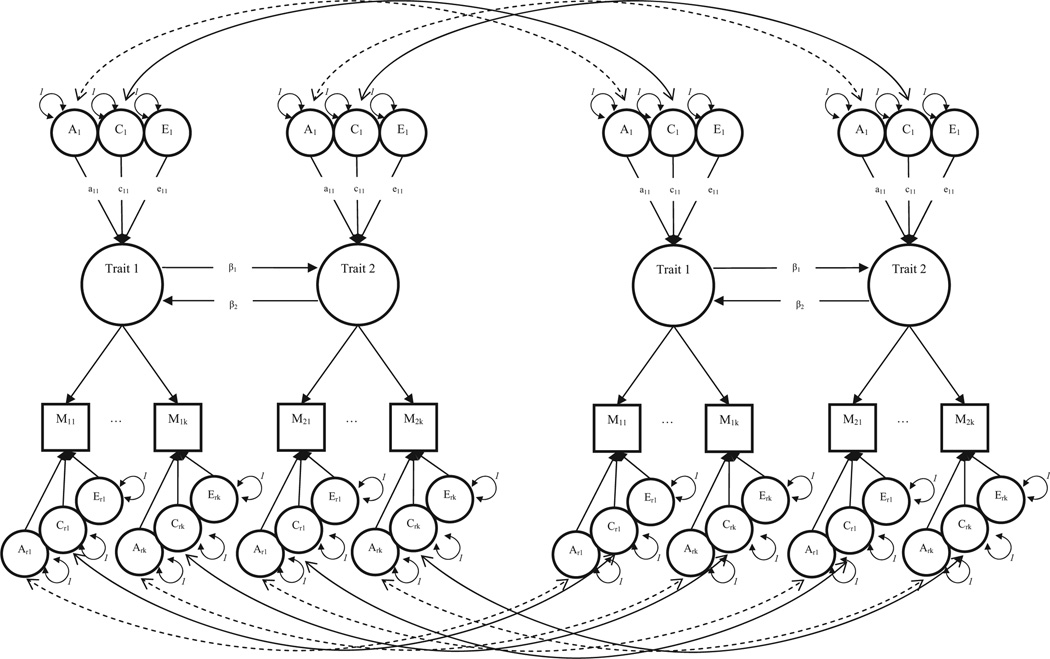
One of the most important limitations of the DoC model is that measurement error can have a nefarious influence on the causal parameters. Observed variables, which are common in political science, have non-trivial levels of measurement error. In simple models, this measurement error is assumed to be stochastic and subsequently ignored. In DoC models, ignoring the possibility of measurement error in any variable that causally influences other variables in the model can bias the parameters (as is the case with measurement error in a predictor variable in an ordinary least squares regression: Heath et al., 1993; Neale and Cardon, 1992). As such, the causal pathway from the variable with more measurement error to the variable with less measurement error is typically attenuated. One way to minimize the problem of measurement error on the estimates of the causal pathways is to rely on measurement theory and construct latent dimensions for the variables of interest. In general, measurement error of the manifest traits with multiple indicators can be accounted for by a confirmatory factor analysis (CFA) or Item Response Theory (IRT) model. Both of these methods should minimize the measurement error in the constructs of interest and, therefore, minimize the impact of measurement error on the causal pathways. Thus, we recommend an estimating model that somehow accounts for measurement error in the manifest variables, such as a confirmatory factor model or some other type of measurement model. A visual depiction of this type of model within the DoC framework is presented in Figure 4.⁴

Figure 4. Bivariate direction of causation model within a structural equation model.

3. Demonstration: Testing causal direction in measures of sex attitudes and psychoticism

The DoC model is particularly useful for testing causal hypotheses about the constructs that are relatively stable across a reasonably broad timeframe, such as personality traits and attitudinal preferences which we use as an example for exploring the DoC model. The connection between personality traits and political attitudes has historically rested on the assumption that personality traits cause people to develop political attitudes. This assumption seems entirely plausible as personality is widely understood as a combination of innate dispositions, personal experiences, and previous behavior (Bouchard, 1994; Cattell, 1957; Eysenck 1990, 1991; Tellegen et al., 1998; Winter and Barenbaum, 1999), while attitudes have typically been viewed as much more malleable across time (Converse, 1964). Recent research has demonstrated that the observed correlations between several personality traits and a variety of political attitude dimensions are primarily a function of shared genetic covariance (Verhulst et al., 2010); however, this research does not explicitly explore the potential causal structure that may exist between the personality traits and the political attitude dimensions.

3.1. Data

Data were collected from 1988 to 1990 by mailed surveys to two large cohorts of adult Australian twins enrolled in the volunteer Australian Twin Registry. Each participant completed a Health and Lifestyle Questionnaire (HLQ), which contained items on socio-political attitudes, personality traits, and wide variety of health-related and sociodemographic measures (Martin, 1987). The sample contains to 7234 individual twins, comprising 3254 complete same sex pairs and 363 unlike sex pairs from 5402 families. The mean age of the twin respondents was 34.1 (SD = 14.0) and 63.8 percent of the respondents were female. The current analysis is restricted to the 1406 male twin pairs, consisting of 814 monozygotic pairs and 592 dizygotic pairs, to avoid the need to estimate sex effects and thus simplify the demonstration.

3.2. Measures

The personality trait we focus on for the demonstration is Eysenck’s Psychoticism dimension. The Psychoticism scale was constructed using six items from the Eysenck Personality Questionnaire (EPQ-R-S, Eysenck et al., 1985; Eysenck and Eysenck, 1997). Responses to the Psychoticism items were in binary format (yes vs. no). The item wording, as well as the parameter estimates from the three separate estimation techniques used to construct the measure, is presented in Table 3. In general, Psychoticism correlates strongly with Authoritarianism and Conscientiousness.

Table 3.

Factor loadings for psychoticism scale (standard errors in parentheses)

Item:	IRT Estimation (ML)		Continuous CFA (ML)		Ordinal CFA (WLS)
Do you stop to think things over before doing anything?	0.517	(0.002)	0.204	(0.020)	0.323	(0.041)
Would you take drugs which may have strange or dangerous effects?	−0.802	(0.004)	−0.415	(0.024)	−0.764	(0.042)
Do you prefer to go your own way rather than act by the rules?	−0.906	(0.009)	−0.568	(0.026)	−0.634	(0.040)
Do good manners and cleanliness matter much to you?	0.704	(0.004)	0.232	(0.021)	0.448	(0.047)
Would you like other people to be afraid of you?	−0.687	(0.004)	−0.202	(0.020)	−0.316	(0.050)
Is it better to follow society’s rules than go your own way?	0.821	(0.003)	0.470	(0.023)	0.639	(0.041)
Abortion	0.906	(0.014)	0.669	(0.015)	0.778	(0.023)
Birth Control	0.754	(0.017)	0.321	(0.016)	0.469	(0.043)
Casual Sex	0.688	(0.032)	0.360	(0.017)	0.580	(0.028)
Chastity	−0.685	(0.020)	−0.452	(0.016)	−0.523	(0.028)
Condom Machines	0.932	(0.008)	0.640	(0.015)	0.856	(0.023)
Gay Rights	0.765	(0.023)	0.563	(0.016)	0.570	(0.028)
Legalized Prostitution	0.843	(0.018)	0.562	(0.016)	0.709	(0.024)
Surrogate Moms	0.763	(0.015)	0.496	(0.016)	0.573	(0.026)
Test Tube	0.747	(0.023)	0.482	(0.016)	0.581	(0.028)

Note: Estimated factor loadings and standard errors for three different latent trait models fit to data for the Psychoticism and Sex Attitudes scales. For the Psychoticism scale IRT estimation gives factor loadings estimated from a two-parameter logistic model using maximum likelihood estimation while for the Sex Attitudes Scale IRT estimation gives factor loadings estimated from a graded response model using maximum likelihood estimation. Continuous confirmatory factor analysis loadings are estimated by treating the binary data as continuous and using maximum likelihood estimation. Ordinal confirmatory factor analysis loadings are estimated from a categorical data model estimated using weighted least squares.

The attitudinal dimension that we explore for the demonstration is constructed from attitudes about sex and reproduction. The Sex Attitudes dimension was constructed using nine items that assess attitudes toward a variety of different issues that deal generally with procreation. Items were responded to in a Wilson–Patterson format consisting of a three-point ordered scale (Yes, ?, No: Wilson and Patterson, 1968). The issues and parameter estimate from the various estimation procedures are presented in Table 4. The Sex Attitudes dimension is analogous to a social/moral values dimension.

Table 4.

Standardized regression results for latent variable models

Item	Manifest Model (ML)		Continuous CFA (ML)		Ordinal CFA (WLS)
Psych → Sex	0.376	(0.122)	0.059	(0.180)	0.124	(0.453)
Sex → Psych	−0.545	(0.107)	−0.367	(0.161)	−0.495	(0.345)

Note: Standardized regression effects for manifest variable (IRT), continuous data (ML), and categorical (WLS) estimations of bidirectional model.

3.3. Models

A total of five models will be compared to assess the direction of causal flow. The first model will have no relation between the Sex Attitudes and Psychoticism. The second and third models will regress Psychoticism on Sex Attitudes and Sex Attitudes on Psychoticism, respectively. The fourth model will contain the regressions found in the second and third models and test bidirectional coupling between the two variables. All four of these models will be compared to a Cholesky decomposition of the Sex Attitudes and Psychoticism variables, with the causal parameters corresponding with the β pathways in the manifest variable Cholesky shown in Figure 3.

3.4. Model fitting

For the demonstration, both manifest variable and latent variable versions of these models will be fit. In the manifest variable versions, scores for the Psychoticism and Sex Attitude scales were estimated using R’s ‘ltm’ library (Rizopoulos, 2006), with the scores for the (binary) Psychoticism scale fit with a two-parameter logistic item response model and scores for the (three-category) Sex Attitudes scale fit with a graded response model. The DoC model was then fit to these trait scores using maximum likelihood estimation in OpenMx (Boker et al., 2011). Two latent variable versions of these models were fit to the raw categorical data in Mplus (Muthén and Muthén, 1998–2010). The first version uses the Maximum Likelihood Estimator and incorrectly treats the categorical data as continuous, while the second uses weighted least squares estimation (WLS) treating the data as categorical. The WLS method allows for efficient estimation of latent variable models with categorical data, but lacks the robustness of fit statistics and accuracy of estimation under missing data that maximum likelihood provides (Lipsitz et al., 1994). As such, the manifest variable versions of these models will be treated as the primary models of interest as both the model estimation and score estimation rely on full information maximum likelihood methods that are more robust to missing data. The latent variable versions serve as both a check on the manifest variable version and a demonstration of direction of causation models for multivariate and categorical data. All models are multiple group, with one model for monozygotic twins and a second model for dizygotic twins, with constraints both across groups and to impose the appropriate genetic structure as described in the introduction. All of the scripts used in this paper can be found at http://www.people.vcu.edu/~crestabrook/.

4. Results

4.1. Manifest variable models

The model fit statistics for the five manifest variable models are presented in Table 1. The −2 log likelihoods for each model will be the primary statistic of interest, which are used for likelihood ratio tests for nested models and to compute AIC for non-nested model comparisons. Degrees of freedom are calculated both for full information estimation and standard structural equation methods.⁵

Table 1.

Model fit statistics for manifest variable models

Model	−2LL	dfFIML	dfSEM	Δ −2LL	ΔdfChol	p	AIC
No Relation	10704.40	4872	12	100.37	3	<.001	906.40
Sex → Psych	10625.06	4871	11	21.04	2	<.001	883.06
Psych → Sex	10615.22	4871	11	11.20	2	0.004	873.22
Bidirectional	10604.19	4870	10	0.17	1	0.683	864.20
Cholesky	10604.03	4869	9				866.03

While both unidirectional models provide an improvement in fit over the norelation model, the best fitting model includes regressions in both directions. The bidirectional model provides improvements in fit over both unidirectional models, whether the Sex Attitudes measure was regressed on the Psychoticism measure (Δ − 2LL = 89.17, Δdf = 1, p < .001) or Psychoticism was regressed on the Sex Attitudes measure (Δ − 2LL = 79.34, Δdf = 1, p < .001). The relationship between Psychoticism and Sex Attitudes cannot be ascribed to a simple unidirectional relationship, but in fact shows strong evidence of reciprocal causation.

The superiority of the bidirectional model is also evident in comparisons with the Cholesky, which serves as the saturated model for this analysis. The bidirectional model shows a better model fit by AIC (AICB = 864.20, AICC = 866.03). This model also shows negligible loss in fit relative to the Cholesky by the likelihood ratio test though these models are not nested (Δ − 2LL = 0.17, Δdf = 1, p = .683). This indicates that the bidirectional model both fits as well as or better than a model with no specified causal direction, and is more parsimonious.

The parameters from the bidirectional model are shown in Table 2, which correspond with the path diagram presented in Figure 3. The regression parameters show a moderate regression of Sex Attitudes on Psychoticism in the positive direction (Raw Est. = 0.456, Std. Est. = 0.376), and a larger negative regression coefficient when Psychoticism is regressed on Sex Attitudes (Raw Est. = −.449, Std. Est. = −.545). When taken together, they denote a negative association between Psychoticism and Sex Attitudes such that more conservative Sex Attitudes drive higher levels of Psychoticism, represented by a model-implied correlation between these two constructs of −0.212. This effect is suppressed by a smaller effect of Psychoticism driving Sex Attitudes in the opposite direction. This model estimates the standardized residual genetic variances for the Psychoticism scale to be 0.248 for the additive genetic component, 0.082 for common environment, and 0.671 for unique environment. The standardized residual genetic, common environment, and unique environment variances for the Sex Attitudes scale are 0.408, 0.283, and 0.611, respectively. The residual genetic components will not sum to one for either variable due to the reciprocal causal structure.

Table 2.

Parameters from bidirectional manifest DoC model

Parameter:	Std. Est.	Raw Est.	SE	p
InterceptSex	0.000	0.130	0.036	<.001
ASex	0.408	0.281	0.095	0.003
CSex	0.283	0.195	0.081	0.017
ESex	0.611	0.420	0.051	<.001
InterceptPsych	0.000	−0.165	0.016	<.001
APsych	0.248	0.123	0.058	0.034
CPsych	0.082	0.041	0.050	0.414
EPsych	0.671	0.334	0.029	<.001
Psych → Sex	0.376	0.456	0.148	0.002
Sex → Psych	−0.545	−0.449	0.089	<.001

4.2. Latent variable models

The analysis applied to manifest variables in the above section can be extended to latent variable models, as depicted in Figure 4. Table 3 contains the standardized factor loadings for several methods of latent trait estimation. The manifest variable analysis in the previous section relied on trait scores estimated from item response models for each scale. These parameter values are included in the ‘IRT Estimation’ column. The results for confirmatory factor models using maximum likelihood (ML) assuming continuous data and WLS assuming categorical data are provided in the ‘Continuous CFA’ and ‘Ordinal CFA’ columns, respectively. Results are relatively consistent over the three methods, with the overall values are much lower for the continuous data models due to attenuation induced by the categorical nature of the data. As can be seen in the Continuous ML factor loadings for both Psychoticism and Sex Attitudes, erroneously treating the ordinal factors as continuous factors severely attenuates the magnitude of the factor loadings.

The standardized regression results for all three methods are shown in Table 4. The results of all three models are relatively consistent, all showing a relatively robust negative effect of Sex Attitudes causing Psychoticism, and a less robust positive effect of Psychoticism causing Sex Attitudes. The continuous data latent variable model shows weaker effects due to the attenuation found in this method with ordinal data, and the weaker effect of Sex Attitudes on Psychoticism in the WLS model prevents the scaling issue that affected the manifest variable models discussed earlier.

5. Discussion

The results presented above denote two methods for conducting a DoC analysis: (1) a two-stage process whereby factor scores are constructed from the raw items in the first stage and then subsequently used as manifest variables in the DoC analysis, and (2) conducting the DoC analysis on the latent factors. While these methods vary in several ways, the results are generally consistent across analyses. Both approaches indicate reciprocal and opposite signed causation driving the relationship between Psychoticism and Sex Attitudes. Specifically, more conservative Sex Attitudes drive higher levels of Psychoticism, while this effect is suppressed by a smaller effect of Psychoticism driving Sex Attitudes in the opposite direction. Therefore, contrary to the broad expectation (Mondak et al., 2010), the personality trait (in this case Psychoticism) does not simply cause people to develop more conservative attitudes. Instead, a much more complex, reciprocally causal relationship exists.

The model comparisons clearly demonstrate that the reciprocal causal model explains the data most effectively. Specifically, this model is clearly superior to both unidirectional models and the unrelated or independent model. Moreover, the Cholesky decomposition, which serves as the saturated model for this type of clustered data, does not fit any better than the reciprocal causation model.

Importantly, the ability to disentangle the causal structure between Sex Attitudes and Psychoticism rests on the discrepant modes of transmission between the two constructs. Sex Attitudes show a significant shared environmental component, while Psychoticism has virtually no shared environmental component. The relationship between the two constructs cannot be described simply by either construct’s genetic structure, but can be parsimoniously described as a simple mix of the two structures. There is no need to invoke a separate genetic structure to describe the cross-twin cross-trait covariances, as would be indicated if the bidirectional model provided an inferior fit to the saturated Cholesky decomposition.

As can be seen in the analysis, the DoC is able to illuminate the complex relationships between constructs that may be very difficult to effectively manipulate in an experimental context or otherwise randomly assign. There are, however, several important issues to keep in mind when conducting a DoC analysis. Primarily, in order to effectively disentangle the causal direction between two constructs, the two constructs must have different modes of transmission (Heath et al., 1993). In the demonstration section, Sex Attitudes are characterized by three separate significant sources of variance – additive genetic, shared, and unique environmental – while Psychoticism is characterized by two – additive genetic and unique environment. As such, the different modes of transmission create differential causal expectations. As the modes of transmission for two constructs become more similar, the ability of the DoC model to determine which causal pathway more adequately captures the relationship between the constructs is greatly diminished. In such cases, the ability to determine causality may require extremely large sample sizes (Gillespie et al., 2003; Heath et al., 1993).

Furthermore, measurement error in the variables may attenuate the potential causal effects. Accordingly, in the demonstration, we either used factor scores derived from an IRT model, or conducted the DoC model on latent traits using a weighted least squares estimator (Muthén and Muthén, 1998–2010). Both of these methods minimize the measurement error in the constructs, allowing for more reliable estimates of the causal effects.

6. Conclusion

When genetic information is coupled with clustered data, a test of causal directionality can be derived. This makes genetic modeling a very effective method for determining the causal effects in cross-sectional data, especially in situations where assessment of the direction of effects is not possible through other means. Accordingly, the use of the DoC model in future research will be able to clarify the causal structure that exists between a wide variety of politically relevant constructs.