Universal collapse of stress and wrinkle-to-scar transition in spherically confined crystalline sheets

Abstract

Imposing curvature on crystalline sheets, such as 2D packings of colloids or proteins, or covalently bonded graphene leads to distinct types of structural instabilities. The first type involves the proliferation of localized defects that disrupt the crystalline order without affecting the imposed shape, whereas the second type consists of elastic modes, such as wrinkles and crumples, which deform the shape and also are common in amorphous polymer sheets. Here, we propose a profound link between these types of patterns, encapsulated in a universal, compression-free stress field, which is determined solely by the macroscale confining conditions. This “stress universality” principle and a few of its immediate consequences are borne out by studying a circular crystalline patch bound to a deformable spherical substrate, in which the two distinct patterns become, respectively, radial chains of dislocations (called “scars”) and radial wrinkles. The simplicity of this set-up allows us to characterize the morphologies and evaluate the energies of both patterns, from which we construct a phase diagram that predicts a wrinkle–scar transition in confined crystalline sheets at a critical value of the substrate stiffness. The construction of a unified theoretical framework that bridges inelastic crystalline defects and elastic deformations opens unique research directions. Beyond the potential use of this concept for finding energy-optimizing packings in curved topographies, the possibility of transforming defects into shape deformations that retain the crystalline structure may be valuable for a broad range of material applications, such as manipulations of graphene’s electronic structure.

Confining crystalline sheets to spherically curved substrates is associated with an unavoidable geometric conflict, because the local hexagonal packing, a planar tiling of equilateral triangles, is incompatible with spherical geometry. According to Gauss’s Theorema Egregium, the distortion of the preferred equilateral packing grows in proportion to the fraction of sphere area covered by the sheet, and consequently the sheet acquires mechanical stresses. Resolving this conflict underlies a host of problems in materials geometry, from assembly of proteins at cell walls (1, 2) to the thermodynamics of phase-separated domains on model membranes (3–5) and, more recently, to the structure and stability of particle-stabilized droplets (6, 7). Remarkably, when the (hexagonal) lattice spacing is much smaller than the lateral dimension of the sheet, a single continuum theory, which uses the classical Föppl–von Kármán (FvK) equations, describes the long-wavelength properties of this diverse range of systems (8).

Studies of this problem fall largely into two groups according to two distinct mechanisms of structural relaxation. The first group, inspired by the classical Thomson problem of packing on spherical surfaces (9), seeks the ground-state ordering for fixed surface topography (8, 10–13), in which the elastic stresses induced by curvature are relieved only by topological defects—“hard” singular zones of a size comparable to that of the unit cell of the lattice, in which the sixfold bond coordination breaks down. The most primitive defect, an isolated fivefold disclination, emerges only when the sheet occupies a finite fraction of the spherical surface (4). The high-energy disclinations typically are preempted by the lower-energy dislocations—pairs of five- and sevenfold disclinations (7, 12, 14). As was shown by Nelson and collaborators (8, 10), these defects are described by singular point-like sources for stress in the FvK equations, whose far-field effect is analogous to point and dipolar charges in electrostatics. The second group of studies, inspired by classical elasticity of plates and shells (15, 16), has focused on the mechanical, long-wavelength response, which is independent of the crystalline order. In this case, the small scale on which elasticity theory breaks down is determined by the sheet’s thickness, and the deformations that relax the elastic cost of confinement are wrinkles and crumples (17), folds (18), and blisters (19), which do not conform to the imposed spherical shape. In comparison with the hard singularities of crystalline defects, these deformations are “soft,” because their characteristic scales decrease with the sheet’s thickness slowly enough so that elasticity theory is valid throughout the sheet.

Here, we propose a conceptual, previously unrecognized connection between these two distinct classes of deformations: both wrinkle patterns and defect distributions are governed by a single, compression-free stress field. Although the compression-free stress field characterizes a defect-riddled or a highly wrinkled state, it is determined solely by the geometric confinement and exhibits no dependence on the bending modulus or the energy of defects; yet it is markedly different from the original (defect-free, wrinkle-free) stress of the unstable, compressed state of the sheet. The existence of a compression-free stress field, which stores the dominant part of the elastic energy but is distinct from the stress of the undeformed state, has been recognized in studies of wrinkling in amorphous sheets (15, 17, 20–22). However, our analysis reveals the universal nature of such a stress field, showing that it can be achieved equivalently by purely elastic deformation of the shape, or by localized, inelastic deformation of the crystalline structure.

To uncover the universal nature of the stress field and its implication for the structure of crystalline sheets, we analyze a model system of circular crystalline patch adhered to a deformable, spherical substrate. The axial symmetry of the system allows us to identify and compute the energy of the two primary modes that relax the cost of conforming to the spherical geometry: a pattern of radial wrinkles decorating the sheet’s periphery (soft buckling mode) and an array of lattice dislocations organized into equally spaced radial chains, which here we call “neutral scars” (hard mode). The mechanical connection between scar and wrinkle patterns is uncovered by analyzing the continuum limit, in which the unit cell size is much smaller than the lateral size of the sheet. In this limit, these distinct structures are found to relax the energetic cost of confinement by the same dominant amount. The subdominant costs of generating these patterns vanish in the continuum limit and depend, respectively, on the underlying energies of defect cores and out-of-plane deformation, the latter cost deriving from both bending of the sheet and deformation of the substrate. The separation between a universal, dominant energy and a nonuniversal, subdominant cost led us to construct a “morphological phase” diagram of this model in terms of two parameters that are proportional, respectively, to the substrate stiffness and to the reduction of area, or confinement, of the bound sheet. A central prediction of our theory is a transition between wrinkle and scar patterns, whose exact value depends on both the stiffness of the substrate and the confinement level.

Model

Our model system is a circular sheet of radius W in contact with a spherical substrate of radius R, such that 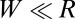(Fig. 1). The interior of the sheet is a 2D hexagonal crystal whose stretching and bending moduli are Y and B, respectively. The surface (adhesion) energy that pulls the sheet over the substrate is 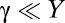. The ratio 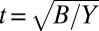is the effective thickness of the sheet, and the von Kármán ratio 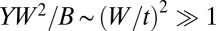, such that the sheet’s resistance to the Gaussian curvature 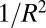imposed by the substrate is dominated by stretching rather than by bending. In contrast to the wetting of a planar substrate, it is impossible to uniformly stretch a sheet on a substrate with nonvanishing Gaussian curvature. The inherent geometric conflict is related to the two distinct sources of strain in the sheet. The “mechanical” strain 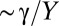, which exists also for planar adhesion, favors uniform, isotropic tension everywhere. On the other hand, a “geometric” strain 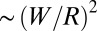is imposed by the spherical substrate as a result of the azimuthal confinement of circles on a flat disk upon projection onto the latitudes of a sphere. The ratio between these two characteristic strains defines a dimensionless measure of confinement (17):

The confinement quantifies the relative effects of the mechanical and geometric strains on the deformation of the sheet, as evidenced by considering the axisymmetric state, in which the stress in the sheet has radial and hoop components:

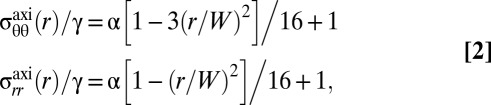where r is the radial distance from the center. [Eq. 2 assumes that the substrate is sufficiently stiff to resist deformations on the scale of W, such that the radial profile of the shape is well approximated by a sphere.] If α is below a threshold 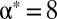(strong mechanical strain), the sheet is under pure tension: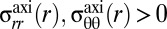. In contrast, for 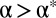(strong geometric strain), the hoop stress becomes compressive 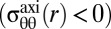at an annulus 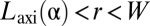, where 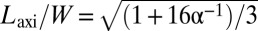(Fig. 1E). If both the costs of bending deformations and defects in the crystalline order are infinite, the compressive state remains stable until delamination occurs when 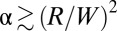(19). However, for substrates of finite stiffness and sheets characterized by a finite cost of lattice defects, the system generically is unstable to the formation of multidislocation “scars” (which leave the substrate intact) and wrinkles (in which the sheet deflects together with the attached substrate), even under weak compression:

In this parameter regime, which we call “weak confinement,” we find for the compressive zone :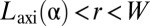

In the axisymmetric state, the total energy stored in the sheet is the sum of the elastic energy minus the adhesive work of area change of the sheet, :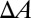

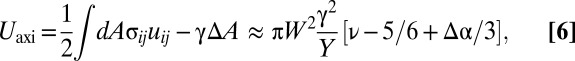where ν is the Poisson ratio. Focusing on the weak confinement regime, we find that the linear stress distribution in the narrow compressive zone leads to analytically tractable equations for both scars and wrinkle patterns, as we show below.

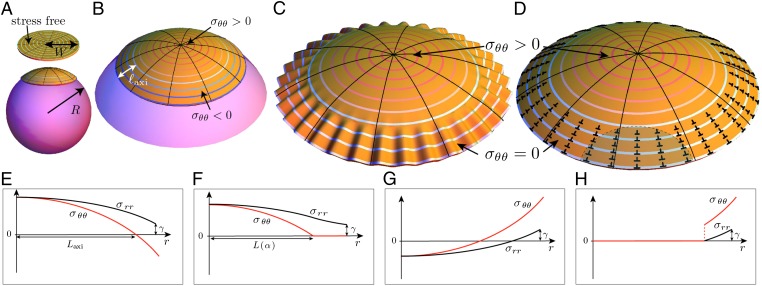
Fig. 1.

Our model system: a circular, crystalline sheet of radius W adhered to a spherical substrate of radius 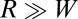. Colors of contours indicate the level of hoop stress: tension (red), vanishing stress (white), and compression (blue). (A) The rest (stress-free) state of the sheet is shown above a schematic of the confinement geometry. (B) The axisymmetric state for confinement 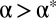: The hoop stress is compressive in a confined zone of width 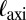near the perimeter. (C) The wrinkle pattern, in which the hoop stress vanishes in the confined zone as the bendability 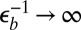. Wrinkles require small deformation of the spherical substrate with the attached sheet. (D) The scar pattern that maintains the imposed spherical shape, in which the stress approaches a profile identical to that of C as the defectability 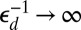. The shaded area indicates the range beyond which dislocation interactions are effectively screened by the boundary 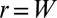. (E and F) The stress fields of the axisymmetric, unstable state (B) and the compression-free state (C and D). (G and H) Profiles of the axisymmetric and compression-free stresses for a negative-curvature (saddle) substrate, in which both radial and hoop stresses collapse in the center of the sheet.

Neutral Scars

A grain boundary is an elementary lattice defect that relaxes stress in crystalline solids. In a sheet, grain boundaries may be viewed as series of edge dislocations along a line (11–14, 23), where the Burgers vectors, 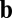, of individual dislocations are (on average) mutually parallel and perpendicular to the line (24). When a curved shape is imposed on a crystalline sheet (11), low-energy grain boundaries may terminate inside the “bulk” of the sheet, and this motif has been dubbed as scars or “pleats” (7). [We prefer the term “neutral scars” (or “scars” for brevity) to distinguish them from charged scars which carry excess disclination charge (7, 11, 23) and to avoid the connotation of shape deformation implied by the colloquial use of “pleat.”] The effect of scars on the elastic energy may be addressed by continuum theory, considering each dislocation as a dipole source for stress, whose far-field distribution may be computed through Green’s function of the biharmonic equation (10). Lattice defects enable purely in-plane relaxation of stress that does not require a deformation of the spherical substrate. Hence, the energy of the scarred sheet may be expressed as

where 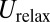is the energy gain due to the interaction of scars with the compressive stress field 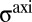, 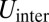is the energy associated with the elastic interaction between all pairs of scars, and 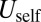is the self-energy of a single scar, which consists of the elastic interaction between all pairs of dislocations along the scar as well as their (inelastic) core energy.

In the axial symmetry of our system, the hoop compression is relaxed by 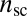radial scars that reside in an annulus 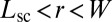, each of which has a length 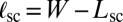and consists of N dislocations with Burgers vectors 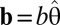. [We find that the ground state structure of a simple periodic array of scars is suitable for the weak confinement conditions addressed here (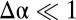). As we discuss later, beyond the weak confinement regime, we expect more complex patterns of dislocations. Note that on spherical substrates, isolated (“charged”) fivefold disclinations can emerge only for 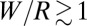. (See refs. 7 and 14.)] The orientation of dislocations corresponds to a missing partial row of lattice sites extending from the boundary along the radial direction and terminating at each defect. Our analysis determines the number 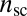and length 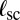of scars, and the number N of dislocations per scar, by minimizing , Eq. 7. Our prime interest is in the continuum limit for weak confinement, where 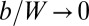at a fixed 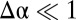(Table S1). Our analysis (see SI Text) shows that in this case, the scars are distributed densely, such that

The relaxation of compression is intimately related to the Peach–Koehler force 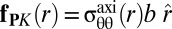, exerted by a compressive component of the stress tensor on a dislocation at distance r from the center (24). Because 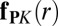is a conservative force and the work associated with “glide” or “climb” approaches to r hence is identical, one may evaluate the elastic relaxation of a defect through the work done by 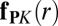when “pulling” dislocations from the edge at 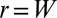into the compressive zone (12, 14). The total relaxation is obtained by summing over all dislocations in the 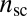scars:

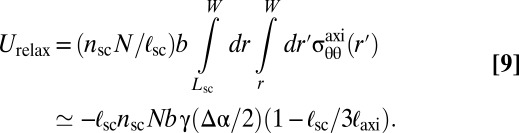Note that a scar may lower the elastic energy (i.e., 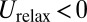) only if .

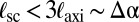The energetic costs 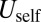, 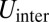may be evaluated similarly, from the elastic energy associated with dislocation-induced stresses (SI Text). It is useful to note that the far-field elastic stress generated by a dislocation at a distance 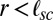from the free boundary of the sheet vanishes beyond distances large compared with 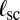. This screening effect (which is not unlike the electrostatic screening of charges near a conducting wall) allows us to evaluate the energies 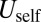and 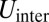to leading order in 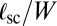. Practically, the leading order term amounts to replacing the circular boundary 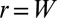with a straight infinite line where the dislocation-induced stress vanishes. With the aid of Green’s function of the biharmonic equation near an infinite stress-free boundary (25, 26), we obtain after summation of all dislocations inside single scars (SI Text)

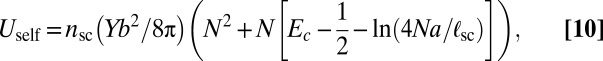where 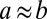is the dipolar separation of the 5–7 disclination pair and 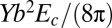is the microscopic cost of the defect core. The first term 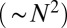originates from interactions between dislocation pairs along the same scar, whereas the second term 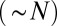results from the self-energy of single dislocations.

The scar–scar interaction energy 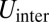is evaluated by summing over dislocation interactions between pairs on separate scars. As depicted in Fig. 1D, scars interact strongly within a lateral distance of order 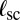, implying 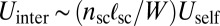. The dense distribution of scars (Eq. 8), together with Eqs. 4 and 9, implies that 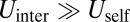and enables us to evaluate the sum over scar pairs, yielding (SI Text)

Furthermore, because 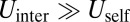, 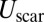is dominated by the sum 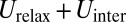. Minimizing over the scar length 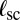and the product 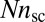, we obtain 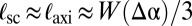and

where 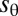denotes the excess hoop strain in the compressive zone that is “absorbed” by scars. Substituting these values for 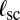and 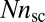in Eqs. 9 and 11, we find

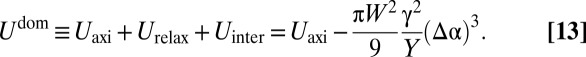Remarkably, we find that in the continuum limit (Eq. 8), the dominant scar energy does not depend on any microscopic features (e.g., the Burgers vector b or the core energy ).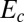

The optimal scar number is found by minimizing the subdominant energy 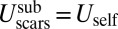subject to Eq. 12, yielding

The subdominant cost depends explicitly on fine features of scars, and is conveniently expressed by a dimensionless group

which compares the elastic cost per dislocation, 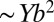, to the elastic energy, 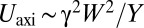, stored in the axisymmetric state. Note that 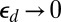in the continuum limit 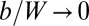. In terms of the defectability ratio, we may write the scar energy as a (singular) expansion in :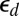

where 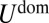, Eq. 13, is independent on 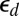and

vanishes as 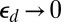(for fixed confinement 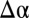). Here, 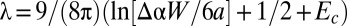is a dimensionless measure of the effective “line tension” of scars.

Eq. 16 reflects a separation of energy scales that is inherent in the scar pattern. A dominant energy is independent on microscopic details and governs two macroscale features: the scar length 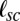and a “slaving” condition (12) between the number of scars 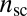and the number of dislocations per scar N. The optimal values of the “fine” features of the pattern are governed by a subdominant energy, which is sensitive to the microscopic parameters (b and 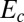). This hierarchical structure is akin to wrinkle patterns, in which a bendability parameter governs the fine features of the pattern (22).

Universal Collapse of Compression

To further understand the physical mechanism underlying the energetic hierarchy of scar patterns, Eq. 16, we analyze the stress field 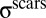. For the scar pattern under weak confinement 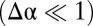, one may evaluate 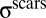by superposing the stress of the equilibrium defect pattern with 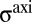of the axisymmetric state (Eq. 2) (SI Text). Notably, one finds that to order 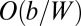and for a dislocation density satisfying Eq. 12, 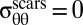for 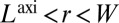. Intuitively, like wrinkles (15, 20–22), scars essentially are a mechanism to collapse compression. As long as hoop compression remains finite, additional dislocations may be pulled from the boundary to relax the compression further. The ultimate residual level of compression (associated with fine-scale stress variation) is determined by the subdominant (self-) energy of scars, Eq. 17 and therefore vanishes asymptotically as .

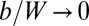Pushing this idea further, we propose that in analogy to wrinkle patterns, the asymptotic stress field underlying the dominant scar energy can be evaluated de novo without any reference to the fine details of scars. Importantly, this principle enables calculations of scarred sheets beyond the weak confinement limit studied here. The derivation of this compression-free stress field [also known as the “membrane limit” or “tension field” in studies of wrinkling phenomena (15)] is given in SI Text, in which we follow the scheme developed in refs. 17 and 22. We find that the compression-free region where scars emerge is 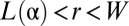, where the stress is

and 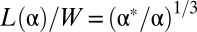. In the unscarred center of the sheet, 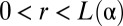, the stress field is purely tensile and is described by Eq. 2 by replacing 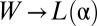and 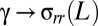. This far-from-threshold, compression-free stress field is depicted in Fig. 1F. We note that although for weak confinement 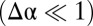one finds 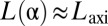(Eq. 4), this feature is not generic. Comparing Fig. 1 E and F, we see that as α increases, the extent 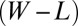of the compression-free (defect-riddled or highly wrinkled) zone exceeds the compressed annulus of the axisymmetric (defect-free, wrinkle-free) state. The difference becomes dramatic in the strong confinement limit 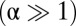in which 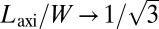whereas .

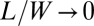This analysis emphasizes that the connection between wrinkles and scars is not the trivial existence of a common unstable state of the confined sheet. Instead, we find a unique, compression-free stress profile (Fig. 1F), strictly distinct from the unstable compressive stress field (Fig. 1E), which is common to both defect-riddled and highly wrinkled states.

Wrinkles vs. Scars

Unlike scars, which relax compression via inelastic lattice defects without deforming the spherical substrate, wrinkling is a purely elastic mechanism that enables the sheet to reach the same compression-free stress field by way of a minute deformation of the sheet and the attached substrate. The wrinkle pattern is described by a smooth deformation of the sheet and the attached substrate in the zone :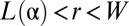

where 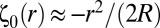is the original spherical profile of the substrate. For sufficiently thin sheets, the amplitude 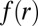becomes arbitrarily small; hence, wrinkles may form even on highly stiff (but not infinitely rigid) substrates. Relaxation of the hoop compression imposes a slaving condition (SI Text):

where 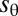again is the excess hoop strain. This relation implies that a fraction 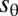of the original length of (undeformed) latitudes is “absorbed” by the wrinkle undulations, such that 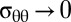. Eq. 20 indicates that the amplitude suppression is tied to divergence of the number of wrinkles, but neither 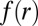nor m appears explicitly in the dominant energy associated with the compression-free stress field, which thus is identical to the energy 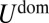of the scar pattern, Eq. 13. The slaving condition for wrinkles, Eq. 20, is the analog of Eq. 12 for scars, constraining the fine features of the patterns to reach an asymptotic, compression-free stress profile.

The wrinkle number m is determined by minimizing the subdominant energy, 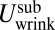. We describe here the central arguments for evaluating 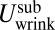and delegate various technical details to SI Text. The three restoring forces underlying 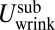are associated with bending rigidity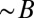, radial tension in the sheet 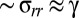, and the stiffness of the spherical substrate, which we assume to be given by a constant K. The respective energies are denoted 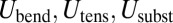. For simplicity, in the current study, we follow ref. 27, assuming that the substrate is modeled by a Winkler foundation, which is characterized by a local restoring force (per area) 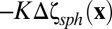to deformations 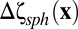of its spherical shape at a surface point . Anticipating the wrinkle number m to diverge as the sheet thickness vanishes and recalling that the slaving condition, Eq. 20, implies inverse proportionality between m and the wrinkle amplitude 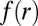, one notices that 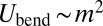, whereas 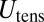and 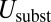both scale as 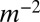. As was observed by Cerda and Mahadevan (27), this implies that the subdominant wrinkle energy 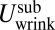is governed by a balance of 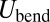and 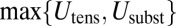, such that the wrinkle number that minimizes the energy satisfies

The parameter 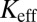is the effective stiffness of a supported, uniaxially stretched sheet, to the formation of wrinkles (27). Implementing this principle for our problem (SI Text), we find that 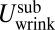and m can be conveniently expressed by defining two dimensionless measures of mechanical response:

Our wrinkling analysis applies to the asymptotic parameter range: 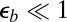, corresponding to very thin sheets or large radial tension, and rigid substrates, 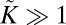. [For 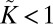, the spherical substrate flattens beneath the sheet (17), invalidating our calculations of the axisymmetric energy 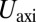and the dominant energy 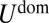of the compression-free stress.] The bendability and deformability parameters enable us to identify three regimes:

(W1) No Wrinkles for .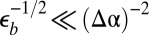

In this regime, the compression is so small that the bending cost 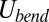is larger than the gain 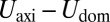due to the compression relaxation. Thus, the compressed axisymmetric state remains stable.

(W2) Tensional Wrinkles for .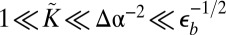

Here, the wrinkle amplitude is suppressed by the cost of out-of-plane pulling against radial tension, 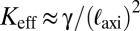, and we find hence:

(W3) Substrate Wrinkles for .

Here, the substrate stiffness is strong, and 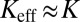. Hence,

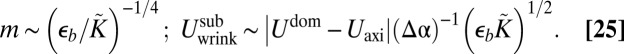Recalling Eq. 15, we may write analogously:

(S1) No Defects for .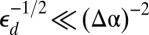

For such weak confinement, the scar self-energy 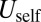outweighs the energy of elastic relaxation, and the unscarred sheet remains stable.

(S2) Scars for .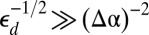

Where scars penetrate through the confined zone, collapsing compressive stress.

Wrinkles-to-Scars Transition

Characterized by an identical compression-free stress field, wrinkle and scar patterns share the same dominant energy 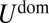, which further implies that subdominant energies alone distinguish between these states. To compare those energies, we assume 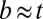, which means that both the Burgers vector b and the thickness t of a (monolayer) crystalline sheet are comparable to the unit cell; hence, 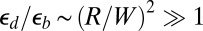. Comparing the subdominant energies of the wrinkles and scars, Eqs. 17, 24, and 25, we note that 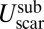is larger [by factor 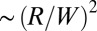] than the subdominant energy of tensional wrinkles, but tensional wrinkles ultimately give way to stiffness-dependent substrate wrinkles when 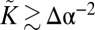. This result underlies a schematic phase diagram, Fig. 2, spanned by the deformability and confinement parameters. For a given confinement, scars are energetically favorable if the substrate is extremely stiff. However, our analysis shows that for a substrate with fixed stiffness, at a deformability range 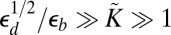, wrinkles are the favorable mechanism for relaxing compression if the confinement level is sufficiently small [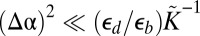]. If confinement is raised gradually (e.g., by increasing the substrate curvature 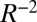), our analysis predicts that equilibrium crystalline sheets undergo a wrinkles-to-scars transition at a critical confinement .

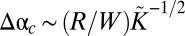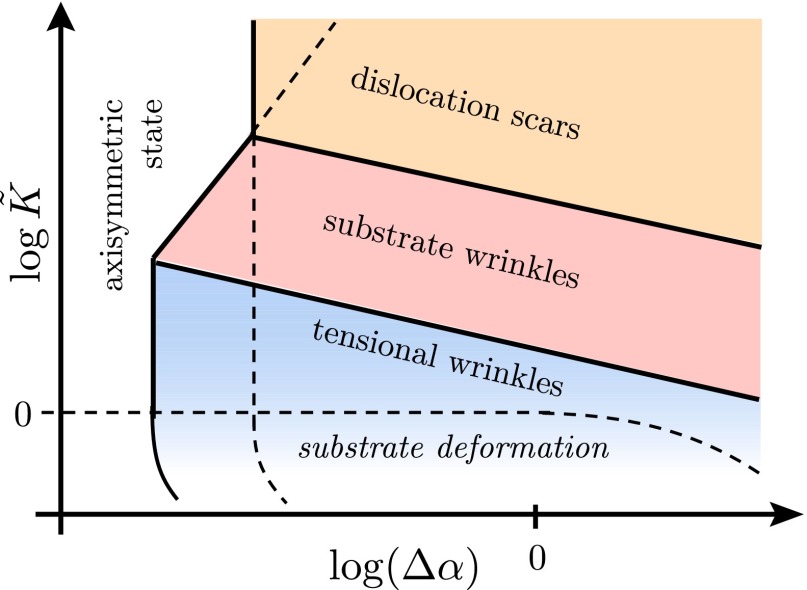
Fig. 2.

Schematic phase diagram of the model spanned by the weak confinement 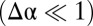and inverse deformability 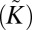parameters, for fixed, high values of the bendability and defectability parameters, 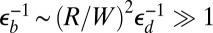. Increasing confinement at a fixed deformability 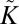, Eq. 23, leads to distinct sequences of pattern transformation, depending on the value of 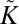: (A) For 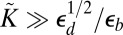(highly stiff substrate), the axisymmetric state is stable for very weak confinement and becomes unstable to scars (S1S2) above a confinement 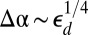(orange). (B) For 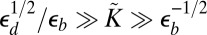, the axisymmetric state becomes unstable to substrate wrinkles (W1W3) at 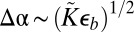(pink), and a wrinkle–scar transition (W3S2) occurs at 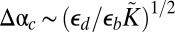. (C) For 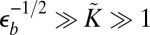, the axisymmetric state becomes unstable first to tensional wrinkles (W1W2) at 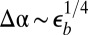(blue), then to substrate wrinkles at 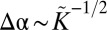(W2W3), and a wrinkle–scar transition (W3S2) occurs again at 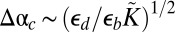. (D) Finally, for 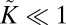, the substrate deforms substantially beneath the sheet [similar to a sheet on a liquid drop (17)]. This regime is not addressed in the current study.

Universality Beyond the Spherical Cap

Our analysis of a circular crystalline patch attached to deformable sphere revealed the existence of a universal, compression-free stress field, which encapsulates the dominant part of the energy 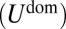of both wrinkle patterns and arrays of neutral scars. This compression-free stress nevertheless is strictly distinct from the original (defect-free, wrinkle-free) stress field, whose high energy 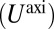underlies the instability of the axisymmetrically compressed state to scars, wrinkles, and potentially other modes of deformation. To demonstrate the generic nature and a few implications of this principle, we briefly discuss some examples that illustrate its applicability for other confining geometries and stress-relieving patterns.

Hyperbolic Shapes.

Consider a circular sheet stretched by a radial tension γ at it edge 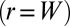on a substrate whose surface has a uniform negative Gaussian curvature, 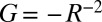. Such a system [inspired by a recent study (28) in which the boundary stress was unspecified] is identical to the one studied above, except that the sign of Gaussian curvature is reversed. The stress in the axisymmetric state is shown in Fig. 1G, where a compressed zone appears at the center of the sheet. Without specific reference to the actual pattern that relieves the compression, it is straightforward to show (SI Text) that collapse of compression is possible only away from the edge 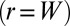, where both radial and hoop stresses vanish (Fig. 1H). Interestingly, the simultaneous collapse of 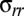and 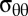implies a jump in 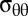at the borderline of the compressive and tensile zones, which requires an appropriate “boundary layer” (29). Although the stress profile (Fig. 1H) is different from the spherical cap (Fig. 1F), the same principle applies. The size of the compression-free zone on the saddle-shaped substrate, as well as the dominant energy of the relaxed states, is independent of fine details of the pattern, be it radial wrinkles, scars, or another stress-relieving mode. The precise features of the minimal-energy patterns of dislocations or wrinkles require a careful analysis of the subdominant energies of both modes, although it is interesting to point out that collapse of stress along both directions in the saddle suggests questions about the degeneracy of radial vs. concentric patterns of wrinkles or scars. The latter pattern was observed in numerical simulations of elastic sheets (28).

Strong Confinement and Large Slope.

Inspired by the Thomson problem (13), many studies have addressed patterns of crystalline defects on curved surfaces: spheres (6, 11), spherical caps (7), “Gaussian bumps” (12), and hyperbolic surfaces (7, 23). In the absence of the simplifying conditions of small slope 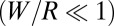and weak confinement 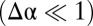assumed in our model system, the patterns of crystalline defects are no longer periodic arrays of radial, neutral scars; hence, finding the optimal pattern of defects that relaxes the curvature-induced stress becomes a daunting task. Nevertheless, the computational complexity —namely, the scar relaxation energy and scar–scar interactions— may be subsumed by the much simpler calculation of the dominant elastic energy stored within the universal compression-free stress that underlies the pattern. Remarkably, the remaining subdominant energy that ultimately determines the fine features (e.g., number of scars) is simply the self-energy of a single scar. We find that the minimization of this energy is tractable and, more importantly, it leads to predictions about the optimal structure of multiscar morphologies: For a given geometry and load, the number of scars 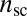diverges as 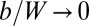whereas the number of dislocations N per scar remains finite. Continuum theory analyses of “Gaussian curvature screening” by dislocations, which previously were applied to multiscar structures [both charged (11) and neutral (7, 14)], essentially are focused on the dominant stress pattern; hence, they resolve only the total dislocation number 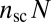and cannot determine the optimal symmetry of scar patterns. In light of our present analysis, we propose that the principle of compression-free stress, as well as analysis of subdominant scar energetics, may be applied to the “charged scar” morphologies to shed light on the ground states of the Thomson problem at the continuum limit 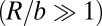(11).

Coexistence and Decoupling of Wrinkles and Scars.

Returning to our original set-up of a sheet on deformable sphere, we note that the universal compression-free stress (Fig. 1F) may be obtained by “mixed” states of wrinkles and scars, parameterized by 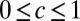, through a generalized slaving condition:

where 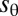is the compressive hoop strain that must be wasted to assure 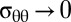in the confined zone, and 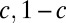are the fractions of that strain absorbed by wrinkles and scars, respectively. Eq. 26 may be viewed as an analog of the “lever rule” for coexisting phases that assures conservation of an extrinsic variable (e.g., mass). It may be shown that for weak confinement, the patterns that minimize the subdominant energy are always one of the two “pure” phases ( 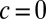or 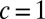). Further numerical work is required to test whether a nontrivial coexistence of wrinkles and scars is possible at other regimes of the parameter space (e.g., strong confinement) or for other confining geometries (e.g., hyperbolic substrate).

Notwithstanding the striking similarity of scar and wrinkle patterns, there exists a profound difference between them. Wrinkles enable collapse of compression but not tension, whereas scars may relax compression and tension alike, by reversing the orientation of each dislocation. It remains an open question whether it is possible for wrinkles to “decouple” from scars, with wrinkles and scars relaxing compression and tension, respectively, in distinct regions of the same sheet.

Concluding Remarks

Our study reveals that two distinct modes of stress relaxation in spherically confined crystalline sheets, wrinkles, and neutral scars both are governed by an identical, compression-free stress profile. Here, we focused on the analytically tractable parameter regime, in which confinement is weak 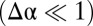and the substrate has a highly stiff, Winkler-type response 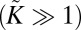. However, we expect that the universal nature of the stress relaxation mechanism remains valid under rather general conditions, such as strong confinement, flexible substrate, and shapes that are not characterized by a constant curvature or axial symmetry. In such circumstances, evaluation of the dominant energy of the compression-free stress and the subdominant energies of wrinkles and scars may be more challenging. Nevertheless, the independence of the dominant energy on the bendability and defectability parameters, and consequently on any fine features of the emerging patterns, is an overarching principle that should serve as a valuable computational tool in the mechanics of crystalline sheets.

Finally, beyond mechanical–geometric applications, one may envision further implications of this study, such as the “strain engineering”—the influence of lattice deformations on the structure of electronic bands in atomic sheets (e.g., graphene) (30). The effect of smooth deformations on electronic properties, such as scattering and tunneling, is qualitatively different from the effect induced by defects. A wrinkle-to-defect transition, whose feasibility is predicted by our study, may provide a channel for manipulating electronic properties through controlled lattice deformations.