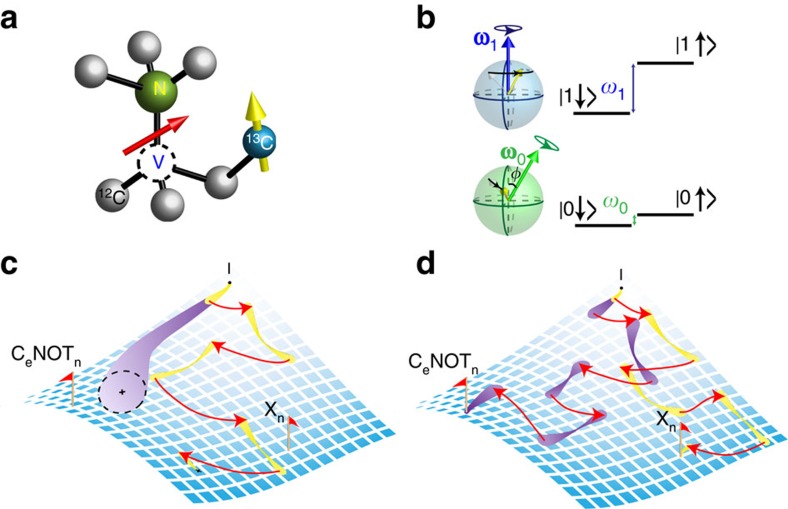
Figure 1. System and approach for steering quantum evolution by DD.

(a) The electron-nuclear spin qubit system. The NV centre electron spin (electron qubit) is coupled to a bath of nuclear spins in a high purity diamond, and a proximal ¹³C nuclear spin (nuclear qubit) is identified by a stronger hyperfine coupling. (b) The conditional local field experienced by the nuclear spin. Because of its coupling with the centre spin, both the quantization axis and the precession rate of the nuclear spin depend on the state of the centre spin. (c,d) Quantum evolution in the operator space, starting from the identity operator I. Under a free evolution (yellow and purple path bundles), the propagator follows the natural ‘landscape’ of the curved operator space. A stroboscopic control (the red arrows) moves the operator to a new position. (c) Propagator evolution in the conventional settings. In a FID experiment (purple path), the coupling between the system and the bath causes non-ideal evolution of the system propagator, and therefore the path of the propagator spreads out in the operator space. In a conventional Carr-Purcell-Meiboom-Gill sequence (yellow path), π-pulses (red arrows) are applied at designed intervals to decouple the system from the environment and can therefore refocus the uncertainty in the system propagator. Yet, in both cases, the quantum dynamics of the system is unconstrained and, in general, the resultant propagator is not the target one. (d) Steering quantum evolution by DD. In contrast to the conventional schemes, one can relax the timing constraint in applying the DD π-pulses and thereby steer the system propagator to the desired points in the operator space. For instance, the C_eNOT_n and the nuclear qubit Pauli-X (X_n) gates can be realized by the purple and the yellow paths, respectively, by tuning the timing parameters in the four-pulse DD sequence.