Population pharmacokinetics of lopinavir and ritonavir in combination with rifampicin-based antitubercular treatment in HIV-infected children

Abstract

Background

The preferred antiretroviral regimen for young children previously exposed to non-nucleoside reverse transcriptase inhibitors is lopinavir/ritonavir plus two nucleoside reverse transcriptase inhibitors. Rifampicin-based antitubercular treatment reduces lopinavir concentrations. Adding extra ritonavir to lopinavir/ritonavir overcomes the effect of rifampicin, however this approach is not feasible in many settings.

Methods

We developed an integrated population model describing lopinavir and ritonavir pharmacokinetics to predict lopinavir/ritonavir (4:1) doses achieving target lopinavir exposures in children treated for tuberculosis. The model included data from 15 children given ‘super-boosted’ lopinavir (lopinavir/ritonavir =1:1) and 20 children given twice the standard dose of lopinavir/ritonavir every 12 h during antitubercular treatment, and from children given standard lopinavir/ritonavir doses every 12 h (39 without tuberculosis and 11 sampled again after antitubercular treatment).

Results

A one-compartment model with first-order absorption and elimination best described the pharmacokinetics of lopinavir and a one-compartment model with transit absorption compartments described ritonavir pharmacokinetics. The dynamic influence of ritonavir concentration on lopinavir oral clearance was modelled as direct inhibition with an E_max model. Antitubercular treatment reduced the oral bioavailability of lopinavir by 77% in children receiving twice usual lopinavir/ritonavir doses and increased ritonavir clearance by 50%. Simulations predicted that respective 27, 21, 20 and 18 mg/kg 8-hourly doses of lopinavir (in lopinavir/ritonavir, 4:1) maintains lopinavir concentrations >1 mg/l in at least 95% of children weighing 3–5.9, 6–9.9, 10–13.9 and 14–19.9 kg.

Conclusions

The model describing the interactions between lopinavir, ritonavir and rifampicin in young children predicted feasible 8-hourly doses of lopinavir/ritonavir resulting in therapeutic lopinavir concentrations during antitubercular treatment.

Introduction

Treatment options are limited for young children with HIV-associated tuberculosis. Lopinavir/ritonavir (LPV/r; co-formulated in a ratio of 4:1) together with two nucleoside reverse transcriptase inhibitors (NRTIs) is the preferred first-line antiretroviral regimen for young children previously exposed to non-nucleoside reverse transcriptase inhibitors [1]. However, rifampicin, a key component of antituberculosis therapy, reduces trough concentrations of LPV by >90% through induction of CYP3A4 and p-glycoprotein expression [2]. We previously demonstrated that acceptable concentrations of LPV were achieved in >85% of children during rifampicin-based antitubercular treatment when extra ritonavir was added to standard doses of LPV/r (‘super-boosted’ LPV with LPV/ritonavir =1:1) [3,4]. However, implementation of ‘super-boosted’ LPV is not practical in many settings as it is complex to prescribe and administer, and ritonavir solution has a short shelf life, hence clinics frequently run out of stock. An alternative approach using double doses of LPV/r achieved adequate concentrations of LPV in adults given rifampicin concurrently [2,5], but results in trough concentrations of LPV below the minimum recommended concentration in the majority of young children [6].

The objective of this study was to build an integrated population model to describe the pharmacokinetics of LPV and ritonavir, taking into account the dynamic interaction between the two drugs, and the effect of concomitant rifampicin-based antitubercular treatment in young HIV-infected children with and without tuberculosis. Furthermore, we employed this model to predict the doses of commercial1y available LPV/r oral solution necessary to achieve LPV trough concentrations consistent with effective antiretroviral activity.

Methods

Study design

The study population and the methods for data collection have been described previously [3,6]. Briefly, 74 HIV-infected children aged 6 months to 4.5 years were enrolled at 3 antiretroviral clinics in South Africa. A parent or legal guardian provided written informed consent to participate in the study, and the research ethics committees of Cape Town, Stellenbosch and Witwatersrand Universities approved the study.

The children received LPV and ritonavir with two NRTIs as antiretroviral treatment. Children without tuberculosis (n=39) received the standard recommended 12-hourly doses of LPV/r oral solution (230/57.5 mg/m²), with a median LPV dose of 11.6 mg/kg. Children with HIV-associated tuberculosis were given either ‘super-boosted’ LPV, with extra ritonavir added to standard 12-hourly doses of LPV/r (n=15), or double the standard dose of LPV/r every 12 h (n=20) together with antituberculosis regimens containing daily 10 mg/kg doses of rifampicin. Eleven children underwent pharmacokinetic evaluation, again, at least 4 weeks after completion of antitubercular treatment, and on standard LPV/r doses.

Sampling and analytical determination

Plasma samples were obtained just prior to an observed dose of LPV/r and at 2, 4 and 8 h after drug administration in all children. Additional samples were collected at 3, 5, 6 and 12 h in a subset of children. All samples were taken after at least 2 weeks of concurrent antitubercular and antiretroviral therapy to allow a pharmacokinetic steady state to be achieved.

LPV and ritonavir plasma concentrations were assayed using validated liquid chromatography-tandem mass spectrometry methods [3]. The lower limits of quantification (LLOQ) were 0.05 for LPV and 0.025 mg/l for ritonavir. Accuracy ranged from 94.3% to 103.0% for LPV and from 93.6% to 105.3% for ritonavir. The intra-day and inter-day precisions of both drugs ranged from 0.14% to 4.72% and from 1.61% to 4.22%, respectively.

Population pharmacokinetic analysis

Population pharmacokinetic analysis was performed using the nonlinear mixed effects modelling software, NONMEM (Version VI, Level 2.0; UCSF, San Francisco, CA, USA). The first order conditional estimation method (FOCE) was used for the estimation of pharmacokinetic parameters. Perl speaks NONMEM (PsN) 3.2.4 and xpose (version 4.1.0) [7,8] were used for model diagnostics.About 5% of the samples were below the lower limit of quantification of the assay and were excluded from the analysis. However, care was taken to ascertain that the model predictions for the excluded samples were compatibly low, so that this exclusion was not expected to bias the results. Different model structures and features were evaluated: one- and two-compartment disposition; zero- and first-order absorption; an absorption with lag time and a series of transit compartments as proposed by Savic et al [9]. The inter-individual (IIV) and inter-occasion (IOV) variability of the pharmacokinetic parameters of LPV and ritonavir were modelled with a lognormal distribution. Using a first-order approximation, the variability of the lognormal distributions are reported as % coefficient of variation (CV).

Several different error structures were tested for the description of the residual unexplained variability (RUV): additive, proportional, combined and exponential error models. The exponential error model was implemented in NONMEM by log-transforming the data. Hence, using a first-order approximation, the variability of the exponential model can be considered as proportional to the observed value.

Model development was guided by precision in parameter estimates, scientific plausibility and the objective function value (OFV) provided by NONMEM, which is assumed to be χ² distributed. Diagnostic tools like visual predictive checks (VPC) and goodness-of-fit plots were also used during model building. In order to account for size differences, allometric scaling based on the median body weight was tested and applied to apparent clearance (CL/F) and volume of distribution (V/F) [10,11]. The following formulas were used (Equations 1 and 2):

$$\mathit{CL}∕F_i=\mathit{CL}∕F_{\mathit{STD}}•{\left(\frac{{\mathit{WT}}_i}{10}\right)}^{0.75}$$ (1)

$$V∕F_i=V∕F_{\mathit{STD}}•{\left(\frac{{\mathit{WT}}_i}{10}\right)}^1$$ (2)

where the WT_i is each patient’s body weight and 10 kg is the median body weight in our population. A maturation model [10,11] was also tested in our model to describe the maturation of clearance.

Once the basic model, including allometric scaling, was developed, a covariate analysis was performed following a stepwise approach similar to Wählby et al. [12]. Candidate covariates included were gender, age and haemoglobin, which were evaluated on all pharmacokinetic parameters. The covariates were incorporated into the basic model to develop the full model, using forward-inclusion (with P=0.05) and followed by backward deletion (with P=0.01). Covariate selection was also confirmed by changes in the standard errors of the parameters, reductions in IIV, IOV and RUV and goodness-of-fit plots.

Two separate population pharmacokinetic models for LPV and ritonavir were developed first. These two models were then integrated into a combined model in which the dynamic interaction between LPV and ritonavir was explored and all parameters simultaneously fitted using all data. Linear and sigmoid relationships were tried to describe the effect of ritonavir concentration on the oral clearance of LPV. A sigmoid relationship was significantly better and used in the final model (Equation 3):

$${\mathit{CL}}_{\mathit{LPV}}={\mathit{CL}}_0•\left(1-\frac{E_{\mathit{max}}•C_{\mathit{RTV}}}{{\mathit{EC}}_{50}+C_{\mathit{RTV}}}\right)$$ (3)

where CL_LPV is the oral clearance of LPV, CL_o is the oral clearance of LPV when no ritonavir is present, E_max is the maximum inhibition effect of ritonavir, EC₅₀ is the ritonavir concentration to reach half of E_max and C_RTV is the concentration of ritonavir.

The effects of antitubercular treatment on the bioavailability and oral clearance of both LPV and ritonavir were evaluated. The relative bioavailability in the control group (standard LPV/r dose, no rifampicin) was assumed as a reference (100%), and the bioavailability of the cohorts on ‘super-boosted’ LPV and ‘double dose’ LPV/r, respectively, were evaluated against the reference. The effect of antitubercular treatment was evaluated as a categorical covariate on bioavailability and oral clearance of both LPV and ritonavir since the effect of rifampicin on enzyme induction could be assumed to be at steady state and within-day change could be neglected.

In addition to antitubercular treatment, the effect of ritonavir dose on the LPV bioavailability was also investigated. In order to investigate both the effect of rifampicin-based antitubercular treatment and the effect of different doses of ritonavir on LPV bioavailability (F_LPV), the following model was used (Equation 4):

$$F_{\mathit{LPV}}=1+\mathit{SLP}•({\text{Dose}}_{\mathit{RTV}}-{\text{Dose}}_{\mathit{RTV}-\mathit{STD}})-\mathit{RIF}$$ (4)

where Dose_RTV and Dose_RTV-STD denote the individual dose of ritonavir (mg/kg) and the median ritonavir dose given in the arm without rifampicin coadministration (3 mg/kg), respectively. The linear relation between F_LPV and ritonavir dose is described by the parameter SLP. RIF is the reduction of LPV bioavailability during antitubercular treatment compared with reference (no rifampicin, median ritonavir dose).

The nonparametric bootstrap re-sampling method, as implemented in PsN, was used in order to obtain standard errors to evaluate the final combined model. Due to the complexity of the model, and since all the pharmacokinetic parameters were estimated simultaneously, the run times were long. Therefore, only 250 non-parametric bootstrap samples were executed to evaluate the accuracy and stability of our final model parameters.

Simulation for optimal dosage

The final combined model was used to perform simulations of different dosing strategies for the weight bands recommended by the World Health Organization for dosing of antiretrovirals in children [1]. Simulation using 1,000 subjects in each weight band (3.0–5.9, 6.0–9.9, 10.0–13.9 and 14.0–19.9 kg) was performed. Trough concentrations were simulated using LPV/ritonavir ratios of 4:1 and 1:1 in different mg/kg doses. The target dose in each weight band was expected to achieve LPV trough concentrations >1 mg/l in at least 95% of children during rifampicin-based antitubercular cotreatment.

Results

Patients and data description

The demographic characteristics and doses of LPV and ritonavir are summarized in Table 1. There were no statistically significant differences in demography between the patients included in the ‘super-boosted’ and ‘double dose’ group. A total of 216, 120 and 96 concentrations of LPV and ritonavir were available from children on standard doses of LPV/r without concurrent antitubercular treatment, children receiving ‘super-boosted’ doses, and children given doubled doses of LPV/r, respectively.

Table 1.

Demographic characteristics of patients

Characteristic	Median	Range
Age, months	21	6 months – 4.5 years
Body weight, kg	10.2	5–17
Gender, male/female	34/10	-
Height, cm	79	58–103
BSA, m2	0.48	0.28–0.69
Haemoglobin, g/l	10.7	5.7–29.7
Albumin, g/l	38	29–47
Dose of lopinavir in control group, mg/kg	11.6	9.4–16.0
Dose of lopinavir in ‘super-boosted’ group, mg/kg	14.0	10.7–18.0
Dose of lopinavir in ‘double dose’ group, mg/kg	23.0	13.8–29.5

BSA, body surface area.

Model description

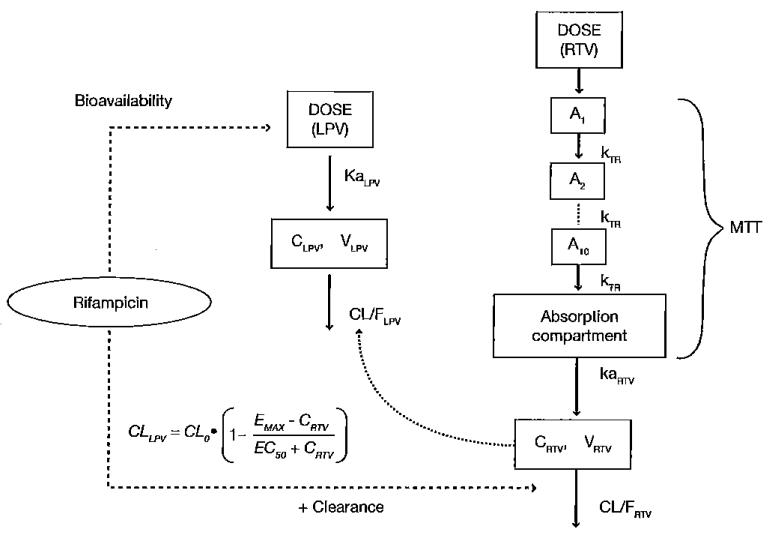
The structure of the final combined model is illustrated in Figure 1. A one compartment model with first-order absorption and elimination best described the pharmacokinetics of LPV. A similar model was used for ritonavir, but the absorption phase displayed more complex pharmacokinetics which was described best by a series of 10 transit compartments. Since a strong correlation was found between the absorption rate constant (k_a) of LPV and ritonavir (r=0.9), the two parameters were estimated as proportional to one another. A similar solution was used for IIV in oral clearance and volume of distribution of ritonavir. Significant covariate relationships were found between body weight and oral clearance and volume of distribution of both LPV and ritonavir. The OFV dropped more than 50 points when allometric scaling was added to the model.

Figure 1.

Structure of the final integrated LPV–RTV pharmacokinetic model

A, amount of transit absorption compartment; C, concentration; CL/F, apparent oral clearance; EC₅₀, the ritonavir (RTV) concentration needed to reach half of the maximum inhibition effect on lopinavir (LPV) oral clearance by RTV (E_max); k_a, absorption rate constant; k_TA, transit absorption rate constant; MIT, mean transit time; V, volume of distribution; V/F, apparent volume of distribution.

Antitubercular treatment significantly reduced LPV bioavailability by 60% and 77% when the ‘super-boosted’ and ‘double dose’ approaches were used, respectively. The additional effect of antitubercular treatment on LPV clearance was not significant and was not included in the model. For ritonavir, the effect of antitubercular treatment was significant on oral clearance, for which different typical values of clearance were estimated for the subjects with and without antitubercular treatment.

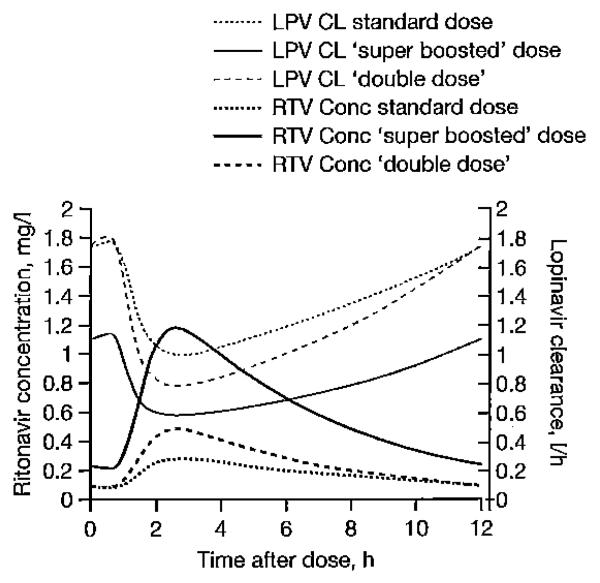
Figure 2 shows the dynamic interaction of ritonavir concentration on oral LPV clearance predicted by the final combined model. When this effect was introduced, the model fitness was significantly improved (ΔOFV=−95.46). Addition of a maturation model [10,11] was not supported by the data.

Figure 2.

The influence of ritonavir concentrations on the oral clearance of lopinavir

LPV CL, lopinavir clearance; RTV Cone, ritonavir concentration.

The typical volume of distribution of LPV was 11.6 l. While the typical clearance of LPV without ritonavir was 4.18 l/h, it should be kept in mind that this value is an extrapolation, since LPV was never given without ritonavir. The typical bioavailability of LPV was 40.5% when ‘super-boosted’ LPV was given and 22.6% when the dose of LPV/r was doubled during antitubercular treatment compared to without antitubercular treatment. Antitubercular treatment increased the oral clearance of ritonavir by about 50%, from 12.7 l/h to 19 l/h. The maximum effect (E_max) of ritonavir concentration on LPV clearance was fixed to 0.9, while EC₅₀ was estimated 0.0519 mg/l. Due to the complexity of the model, numerical instability was experienced when we attempted to estimate all of the parameters simultaneously. Consequently, the E_max was fixed to 0.9. This value was estimated when ritonavir parameters were fixed and only LPV parameters estimated. The population pharmacokinetic parameter estimates for the final combined model are shown in Table 2. All the parameters were estimated simultaneously.

Table 2.

Population pharmacokinetic parameter estimates for both lopinavir and ritonavir in final combined model

		Bootstrap
Parameters	Final model estimates	Mean	95% CIa
Lopinavir
CL/F, l/hb	4.18	4.42	3.41,5.42
V/F, lc	11.6	11.8	9.20, 14.49
ka, h−1	0.74	0.771	0.432, 1.108
Sloped	0.021
RIF on Fe	0.832
Ff
Super-boosted dase	40.5%	45.9%	36.3, 55.5%
Double dose	22.6%	22.5%	14.1, 30.9%
IIVV, %CV	56.6	54.5	32.1,70.2
10V ka, % CV	76.2	78.7	37.5, 100.7
10V F, % CV	51.8	50.8	30.9, 64.8
RUV	0.304	0.311	0.252, 0.349
Ritonavir
CL/F, l/hb
No TB and after TB	12.8	13.0	10.5, 15.5
With TB	19.1	18.5	13.9, 23.1
V/F, Ic	105	105	80.7, 129.5
ka h−1	2.31	2.55	0.54, 4.57
MTT, h	1.28	1.21	0.80, 1.62
IIV CL, % CV	72.8	72.7	61.2, 81.6
10V CI, % CV	41.6	40.0	21.2, 52.6
IIVV, % CV	43.3	42.4	30.3, 56.2
10V MTT, % CV	31.1	46.9	23.6, 65.8
IOV ka, % CV	98.1	104.3	78.5, 120.3
RUV	0.339	0.342	0.291, 0.372
Lopinavrr-ritonavir interactiong
Emax	0.9 (fix)
EC50, mg/l	0.0519	0.0492	0.0270, 0.0715

^aCI from 250 bootstraps.

^b(1).

^c(2).

^dSlope between ritonavir dose (mg/kg) and bioavailability of lopinavir.

^eThe reduction of bioavailability of lopinavir caused by rifampicin (4).

^fRelative bioavailability of lopinavir.

^g(3). CI, oral clearance; CV, coefficient of variation; EC₅₀; the ritonavir concentration needed to reach half of maximum inhibition effect on lopinavir oral clearance by ritonavir (E_max); F, bioavailability; IIV, interindividual variability; IOV, interoecasional variability; k_a, oral absorption rate; MTT, mean transit time; RIF, rifampicin; RUV, residual unexplained variability; TB, antituberculosis treatment; V, volume of distribution.

Model evaluation

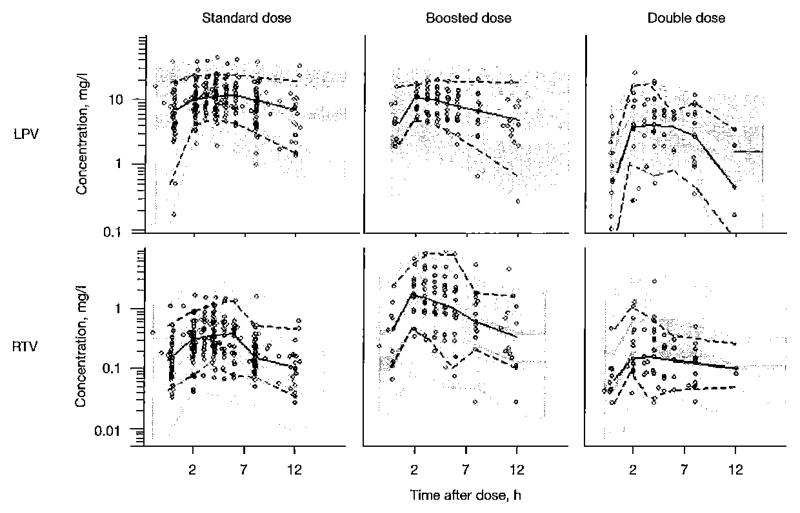
Figure 3 shows visual predictive check plots stratified by different LPV and ritonavir dose strategies. The results of 1,000 simulations from the final model demonstrated the adequacy of the model and indicated that the model had good properties to investigate alternative dosing strategies using simulation. The bootstrap results (Table 2) confirmed the robustness of the final model.

Figure 3.

Visual predictive check of the final combined model for LPV and RTV stratified for regimen

From left to right are shown: standard, ‘super-boosted’ and ‘double dose’ approaches. The solid line is the median of the observed data and the dotted lines are the 5th and 95th percentiles of the observed data. The grey shaded areas are the 95% Cls for the median, 5th percentile and the 95th percentiles of the simulated dilta (n=1,000), Observed concentrations are displayed as circles. LPV, lopinavir; RTV, ritonavir.

Simulation for optimal dosage regimen

Optimal LPV/ritonavir dose recommendations during rifampicin coadministration are presented in Table 3. Simulations predicted that children weighing 3–5.9, 6–9.9, 10–13.9 and 14–19.9 kg need respective doses of 52, 40, 35 and 30 mg/kg LPV/r in 4:1 ratio every 12 h in order to maintain LPV concentrations >1 mg/l in at least 95% of children. An 8 hourly dosing strategy would require lower doses of 27, 21, 20 and 18 mg/kg for the respective weight bands. When giving ‘super-boosted’ LPV (ratio 1:1), the model predicted that LPV doses of 22,16, 14 and 12 mg/kg twice daily are needed in children weighing 3.0–5.9, 6.0–9.9, 10.0–13.9 and 14.0–19.9 kg, respectively.

Table 3.

Predicted optimal dosage regimens of LFV/ritonavir when rifampicin is coadministered based on simulations using the final combined model

	LPV:ritonavir =4:1		LPV:ritonavir =1:1 12-hourly LPV dose, mg/kg
Body weight, kg	12-hourly LPV dose, mg/kg	8-hourly LPV dose, mg/kg
3.0–5.9	52	27	22
6.0–9.9	40	21	16
10.0–13.9	35	20	14
14.0–19.9	30	18	12

LPV, lopinavir.

Discussion

Despite the complexity of combined antitubercular and antiretroviral therapies, survival of patients presenting with HIV-associated tuberculosis is significantly improved when antiretroviral treatment is introduced during antitubercular therapy [13–15]. However, combined treatment options are limited for young children, especially children who have been exposed to nevirapine for prevention of mother-to-child HIV transmission, and those younger than 3 years, in whom efavirenz cannot be used. In young children, there is very little data about the pharmacokinetics of LPV and ritonavir when coadministered with rifampicin-based antitubercular treatment. We described the pharmacokinetics of LPV using an integrated population model based on 2 studies evaluating LPV and ritonavir concentrations in children with and without tuberculosis in order to predict the optimal dose of LPV/r (in a 4:1 ratio) in young children treated with a rifampicin-based regimen.

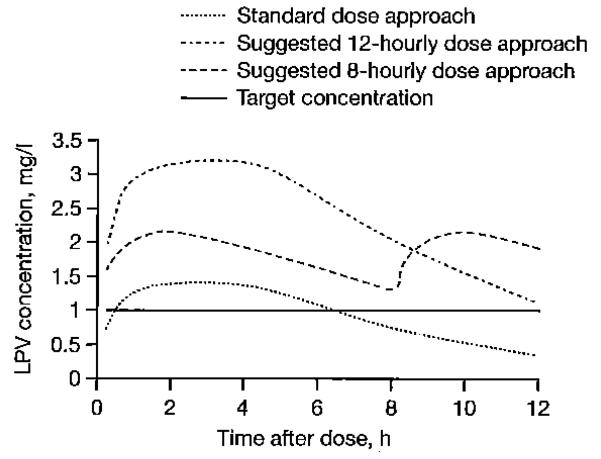
LPV target trough concentrations (>1 mg/l) were achieved in the control group who received standard doses of LPV/r without rifampicin). In children concurrently administered rifampicin-based antitubercular treatment, ‘super-boosted’ LPV almost always achieved adequate trough concentrations of LPV, but the strategy using doubled doses of LPV/r failed. Simulations from our model indicated that, using LPV/r oral solution twice daily, LPV doses would need to be increased dramatically during antitubercular treatment, especially in children with lower body weights. For children weighing 3.0–5.9 kg, the LPV dose needed to attain the target would be 52 mg/kg every 12 h, which considerably exceeds the doses used in clinical practice and could lead to the appearance of adverse events. Consequently, an 8-hourly dosage regimen was investigated to reduce doses, and indeed this three times daily approach would require, in children weighing 3.0–5.9 kg, only 27 mg/kg. The total daily doses required to maintain therapeutic LPV concentrations were lower using 8-hourly doses. The 5th percentiles of simulated LPV concentrations using the original and the proposed dosage regimens in a typical patient (the patient who has a median age and median body weight) when LPV/r was given as standard ratio 4:1 are presented in Figure 4. The predicted 95th percentile of LPV trough concentrations for an 8-hourly approach is 15.8 (5.61, 31.5), 12.4 (5.2, 24.2), 12.6 (5.7, 25.8), 9.5 (5.1, 16.6) mg/l for children weighting 3.0-5.9, 6.0-9.9, 10.0-13.9 and 14.0-19.9 kg, respectively. These values are lower than those predicted for 12-hourly doses of super-boosted LPV: 22.2 (8.3, 41.7), 14.6 (6.2, 28.3), 13.3 (5.9, 26.3) and 10.9 (5.9, 23.2), respectively.

Figure 4.

The 5th percentile of simulated LPV concentrations obtained for a typical patient using different dosage regimens

The solid line is the target concentration of 1 mg/l. LPV, lopinavir.

The bioavailability of LPV was estimated considering the effects of both rifampicin and ritonavir. Our model predicts that exposme to LPV would drop by 83.2% if antitubercular treatment was concomitantly given without any further dose adjustments. LPV bioavailability increased by 2.1% for each mg/kg of ritonavir added to the dose. Even though the relationship between ritonavir dose and bioavailability is probably quite complicated, in our model it was described using a linear proportionality. This choice was compelled by the limited range of ritonavir doses available in the dataset, and should not be used too far outside the tested range. We expect it to provide reasonable predictions for our purposes. During antitubercular treatment, the relative bioavailability of LPV was reduced to 22.6% of the reference in children receiving twice of usual dose of LPV/r, while for children given ‘super-boosted’ LPV this value almost doubled, reaching 40.5%. IOV in k_a of LPV was significant in the model, whereas IIV in LPV k_a was not supported by the data, pointing towards a greater relevance of occasion- rather than subject-specific changes during the absorption phase.

The typical oral clearance of ritonavir when concurrently administered with rifampicin was 19.1 l/h, an increase of about 50% compared to the value estimated without antitubercular treatment. Our model is the first to describe the dynamic effect of ritonavir concentrations on the clearance of LPV in children using an integrated model. The EC₅₀ was estimated to be 0.0519 mg/l, which is a low value when compared to normally achieved ritonavir concentrations which supports the potency of ritonavir as an inhibitor. In Figure 2, the change of LPV oral clearance due to ritonavir concentrations can be seen for each dosing strategy.

Body weight was introduced as allometric scaling for oral clearance and volume of distribution of both LPV and ritonavir which is in agreement with previous studies in children [16,17]. Jullien et al. [16] observed a 39% increase in oral clearance of LPV after the age of 12 years for boys. The age range in our dataset (6 months to 4.5 years) might explain why age and gender were not significant covariates in our model. A maturation model was not supported by our dataset, probably due to lack of data in children below 1 year of age [18]. Our model could not be used to confidently predict the doses of LPV/r achieving the target concentrations beyond the range of the available data. Moreover, the pharmacokinetics, efficacy, safety and feasibility of the 8-hourly dosing approach needs to be evaluated prospectively in children.

In conclusion, a population pharmacokinetic model was developed to simultaneously describe the pharmacokinetics of LPV and ritonavir in young children, capturing the drug–drug interactions among LPV, ritonavir and rifampicin. Allometric scaling was used to scale oral clearance and volume of distribution of both LPV and ritonavir. Hence, smaller children receiving rifampicin-based antitubercular treatment require higher mg/kg doses of LPV/r (in 4:1 or 1:1 ratio) than larger children. Oral clearance of LPV was inhibited by ritonavir concentrations in a sigmoid relationship. Our model was used to predict the doses of LPV/r oral solution needed to maintain therapeutic concentrations of LPV during antitubercular treatment and suggests that an 8-hourly dosing regimen should be evaluated in young children.