Excitable behaviour in amoeboid chemotaxis

Abstract

Chemotaxis, the directed motion of cells in response to chemical gradients, is a fundamental process. Eukaryotic cells detect spatial differences in chemoattractant receptor occupancy with high precision and use these differences to bias the location of actin-rich protrusions to guide their movement. Research into chemotaxis has benefitted greatly from a systems biology approach that combines novel experimental and computational tools to pose and test hypothesis. Recently, one such hypothesis has been postulated proposing that chemotaxis in eukaryotic cells is mediated by locally biasing the activity of an underlying excitable system. The excitable system hypothesis can account for a number of cellular behaviours related to chemotaxis, including the stochastic nature of the movement of unstimulated cells, the directional bias imposed by chemoattractant gradients, and the observed spatial and temporal distribution of signalling and cytoskeleton proteins.

The ability of cells to direct movement in response to spatial differences in the concentration of external chemoattractants has fascinated biologists for over a century. Chemotaxis is of great important for the proper functioning of both single-cell and multicellular organisms. It allows single cell organisms to search for nutrients. It guides cells of the immune system to sites of infection. Unfortunately, chemotaxis is not always beneficial, as it also directs cancer cells during metastasis.

There are two fundamental approaches that allow cells to sense and respond to chemoattractant gradients. Cells performing temporal sensing compare concentrations of chemoattractants over time, and make directional decisions based on the temporal changes in receptor occupancy levels. The chemotactic behaviour of bacteria, particularly E. coli, is the best understood temporal sensing mechanism in biology. The temporal sensing strategy is appropriate for small, fast moving cells that can cover an area quickly – E. coli cells move at approximately ten body lengths per second – but also have chemoattractant receptors that are localized in the cell. Larger, slower cells – a classification that includes most if not all of chemotactic eukaryotic cells – employ a spatial sensing mechanism. In this strategy, cell surface receptors need to be spaced sufficiently far that a gradient of receptor occupancy is formed and can serve as the basis for making directional decisions.

Probably the best-studied chemotactic, eukaryotic cells are the social amoeba, Dictyostelium discoideum, as well as the biochemically-similar system in mammalian neutrophils^{1, 2}. Dictyostelium carries out two forms of chemotaxis. During their normal life cycle, they use folic acid gradients to direct their movement in search of bacteria. However, in starvation conditions, Dictyostelium cells develop the ability to produce and secrete cAMP, which is used by cells to aggregate chemotactically. These aggregates eventually form fruiting bodies and spores that allow cells to survive. While the response to these two chemotactic signals is similar, there are some differences. Chemotaxis to cAMP, which is mediated by G-protein coupled receptors, is better understood. To date, the identity of the folic acid receptor is unknown.

The spatial sensing strategy involves the coordinated action of three separate processes^3–5. Clearly, cells must be able to discern receptor occupancy gradients – what we refer to as static spatial sensing – independent of any motility. Cells must respond to the sensed gradient by focusing motility in the direction of the gradients. Finally, cells polarize by developing distinct leading and trailing edges. This polarization, which need not be permanent is usually induced by migrating in gradients, but can also appear after spatially uniform stimulation or even in the absence of any chemoattractant.

In recent years, we have seen a fundamental change in our understanding of chemotaxis in Dictyostelium and neutrophils, prompted by the growing evidence that the actin cytoskeleton and other signalling proteins display behaviour, such as propagating waves, that is consistent with the presence of an excitable system^6–14 (Fig. 1; sidebar). We and others have hypothesized that an excitable system couples receptor occupancy to actin polymerization. Here, we review some of the basic features of the chemotactic response in amoeboid cells, and highlight the role played by the excitable network hypothesis.

Figure 1. Excitable behaviour in chemotactic, eukaryotic cells.

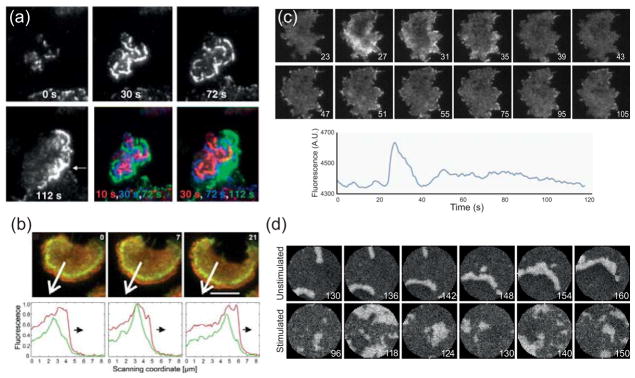
(a) Total internal reflection fluorescent (TIRF) microscopy images of neutrophil-like HL-60 cells expressing Hem-1-YFP (a subunit of the Scar-WAVE compound) continuously exposed to chemoattractant. The outwardly propagating waves eventually develop into a polarized accumulation of Hem-1 at the leading edge (arrow at 112 s). The last two panels overlay successive Hem-1 distributions. (Reprinted with permission from Ref. 11.)(b) TIRF images of Dictyostelium cells expressing GFP-coronin and mRFP-LimEΔ (a marker for newly polymerized actin). Bottom panels, which plot the fluorescence intensity in the direction of the arrow, show the wave front propagating. Scale bar is 5 μm. (Reprinted with permission fro Ref. 6. Copyright 2009 Biophysical Society.)(c) Accumulation of GFP-tagged Hspc-300 (the Dictyostelium homolog of Hem-1) in response to a sudden stimulation (at 25 s) of chemoattractant. The lower panel shows the average intensity plotted over time, with its large peak followed by a slower, second phase. (d) Simulations of excitable behaviour in both unstimulated and stimulated cells. (Panels (c) and (d) are reprinted with permission from Ref. 7. Copyright 2010 National Academy of Sciences USA.)

Sidebar. Excitable systems.

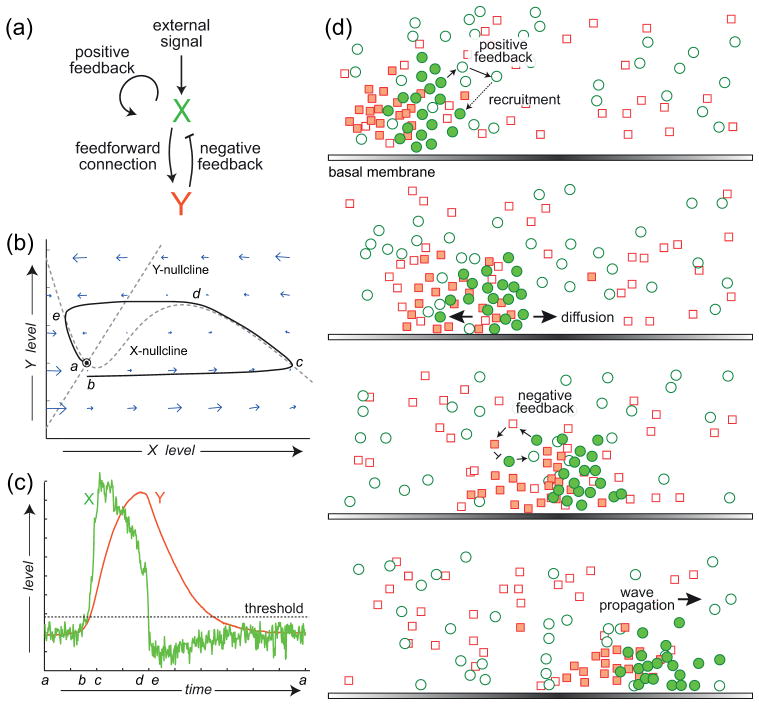
The study of excitable systems and media dates to the Hodgkin-Huxley equations describing action potentials in neurons though is now an active area of applied mathematics. An excitable system is a dynamical system that operates at a stable point (Fig. 2a–c). A small amplitude perturbation away from this equilibrium leads to a small responses. However, if the size of the perturbation is sufficiently large, then the system undergoes a large scale, transient response referred to as a “firing”. After the activation of the system there is a refractory period during which the state goes below the equilibrium point. Moreover, during this period no further firings can take place. Activator-inhibitor systems are a common form of a two-component excitable system, where the activator includes a strong autocatalytic positive feedback loop, as well as a negative feedback loop through the inhibitor (Fig. 2b). Substrate depletion systems are the other common form of an excitable system – in this case, the basic double feedback topology (one positive, one negative) is maintained, but the interaction “arrows” are reversed. The term excitable medium is used if the components of the system are diffusible, in which case the components of the system will be seen to propagate as waves (Fig. 2d). In this case, the refractory period means that after a wave goes through a point, a certain period of time must pass before a second wave may go through. Colliding waves thus appear to annihilate each other.

Motility in unstimulated cells

Actin waves are observed in unstimulated cells or cells that cannot couple receptor occupancy to the signalling network⁶. For this reason it is worth first considering motility of cells in the absence of chemoattractant stimuli. The motile behaviour of cells can be described in two ways. Traditionally, researchers have tracked the net displacement of the cell centroid over time, presenting a global description of cell movement^15–17. However, amoeboid motility is achieved through the extension of pseudopods^{18, 19}. There has been much progress in the characterization of these actin-rich protrusions enabling researchers to explain the observed trajectories of migrating cells in terms of the dynamics of pseudopod formation. This research has benefitted greatly by computational image analysis tools^20–24.

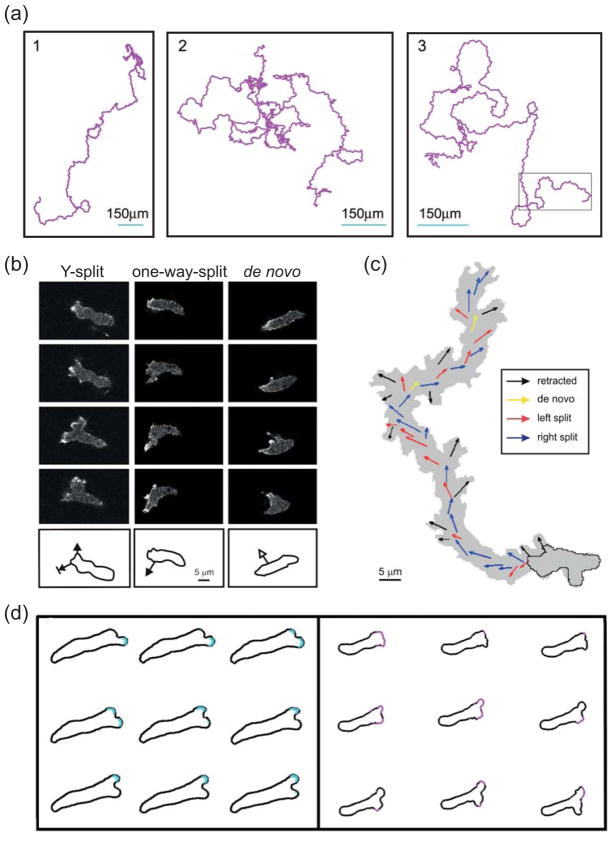
In the absence of any chemoattractant, Dictyostelium cells move constantly and, over time, the direction of movement is random (Fig. 3a). However, as observed over shorter periods of time, the movement displays strong correlation, or persistence, allowing cells to move in relatively straight lines over this time frame^{25, 26}. Persistence enables cells to move over larger distances and increases the likelihood of finding a target²⁵.

Figure 3. Motility of unstimulated cells.

(a) Three 10-hour trajectories of Dictyostelium cells moving in the absence of external stimuli. (Reprinted with permission from Ref. ²⁵.)(b) Confocal images showing typical extensions of pseudopods in unstimulated Dictyostelium cells. Images are at 8 s intervals. In a Y-split, the existing pseudopod splits in two, of which one is eventually retracted. In a one-way-split, a new protrusion is made at the base of an existing pseudopod. De novo pseudopods are those that appear where no recent pseudopod activity has been observed. The outlines below show the direction of the growing pseudopod superimposed on the outline of the earliest image. (c) A 14-minute trajectory of a moving cell with the coloured arrows depicting the direction of the different types of pseudopodia. (Panels (b) and (c) reprinted with permission from Ref. ²⁶.) (d) Pseudopod splits observed in a microfluidic chamber (left) and simulations of an excitable system driving cell protrusions (right). The cell outlines are approximately 2 (left) and 2.5 (right) seconds apart. (Reprinted with permission from Ref. ³⁰.)

The extension of a single pseudopod is not sufficient to translocate the cell in any significant way²⁶. Instead, cells coordinate their activity so that the location of new protrusions is biased in favour of existing pseudopods and it is this coordination that endows cells with their persistence²⁷. Careful analyses of the dynamics of protrusions have revealed the existence of two types of pseudopods, based on where they appear in the cell^{26, 28} (Fig. 3b,c). The first and predominant class forms as a split from an existing pseudopod at roughly 60° from the direction of the mother pseudopod and leading to a “Y” morphology. The second class, referred to as de novo or lateral pseudopod, is one that appears at a location in the cell where no previous pseudopods are found. Data on the growth period of each pseudopod, length distribution, and the time interval between formation of two pseudopods reveals large variability. Growth periods and length distributions are approximately the same, between the two types²⁶. Moreover, the interval between any two pseudopods does not depend on the classes of the two. These findings suggest that the mechanism by which pseudopods are formed has a strong stochastic component and, at least in unstimulated cells, the nature of the pseudopod does not depend on where it is formed.

Excitable systems are an appealing way of describing the dynamics of pseudopod extensions for several reasons. Their emergence can be explained as the stochastic triggered firing of an excitable system^{3, 26, 29, 30}. If the threshold level (Fig. 2c) of the excitable system is the same throughout the cell, then, over time, the firing rate will show no spatial dependence and so pseudopod activity (and hence movement) will appear to be random. This model covers the long-term distribution of the pseudopods, but does not capture short time statistics. This requires that cells remember the location where pseudopods emerge so as to bias the likelihood that subsequent pseudopods are formed at these sites. This memory can be in the form of a local positive feedback that lowers the threshold of activation at the sites of existing pseudopods, but can also be accompanied by a global negative feedback that raises the threshold for activation and hence suppresses pseudopods elsewhere³¹.

Figure 2. Dynamical description of excitable behaviour.

(a) Schematic of an activator (X)-inhibitor (Y) system, a common framework for studying excitable systems. The system has an autocatalytic positive feedback loop and a negative feedback loop through the inhibitor. (b) Phase-plane description of the dynamics of the excitable system. The intersection of the two nullclines (lines for which the level of one component remains constant) denotes the equilibrium, which is dynamically stable. In the absence of perturbations, the system remains there (labelled “a”). A sufficiently large disturbance leads to a large trajectory is phase-space (b to c to d to e) before returning to the equilibrium. (c) Trajectories of the activator (green) and inhibitor (red) as a function of time. Note the sub-basal excursion in the level of the activator, (d to e) which marks the refractory period of the excitable system. (d) Cartoon illustrating how an excitable activator-inhibitor system can give rise to propagating waves. The positive feedback loop means that functional (shaded green circles) activator molecules recruit other activator molecules (open green circles), thus propagating. They also activate inhibitor molecules (shaded red squares) which turn off the activity. (Reprinted with permission from Ref. 3. Copyright 2012 Elsevier Inc.)

Several models have been proposed that used this paradigm for describing cell motility, either to account the appearance of pseudopods³¹ or to explain the underlying signalling activity that can then direct actin polymerization^{12, 29, 30, 32–35}. Simulations in which pseudopods are described as discrete events recreate the statistics of cell displacements in unstimulated cells³¹. Models also direct cells in the correct manner showing both correct cellular trajectories and realistic cellular morphologies for amoeboid motility, including the appearance of pseudopod splits^{30, 33, 34} (Fig. 3d) as well as lamellipodial protrusion and retraction³⁶.

Response to spatially uniform stimuli

The response of cells to chemoattractant stimulus can be observed in a number of ways. One of the earliest descriptions was based on a morphological response, known as a cringe. Shortly after the addition of stimulus, cells stop moving, round up for 20–30 seconds, before resuming motion³⁷. Most of our quantitative understanding of the response to chemoattractant, however, comes from tracking the translocation of fluorescently fused proteins after stimulation (Fig. 4). Upon the application of a spatially uniform stimulus, a number of cytosolic proteins, including several PH-domain containing proteins (e.g. PKB³⁸, CRAC³⁹) translocate to the membrane. These proteins are found preferentially at the front of migrating cells. Other proteins, most notably the tumour suppressor PTEN that is membrane-bound and found at the rear of migrating cells, are released from the membrane^{40, 41}. These responses, however, are transient, as the proteins return to their pre-stimulus locations despite continuous receptor occupancy (Fig. 4). Neither the means by which cells achieve adaptation, nor the molecular identity of the components involved is completely clear.

Figure 4. Response to spatially uniform stimuli.

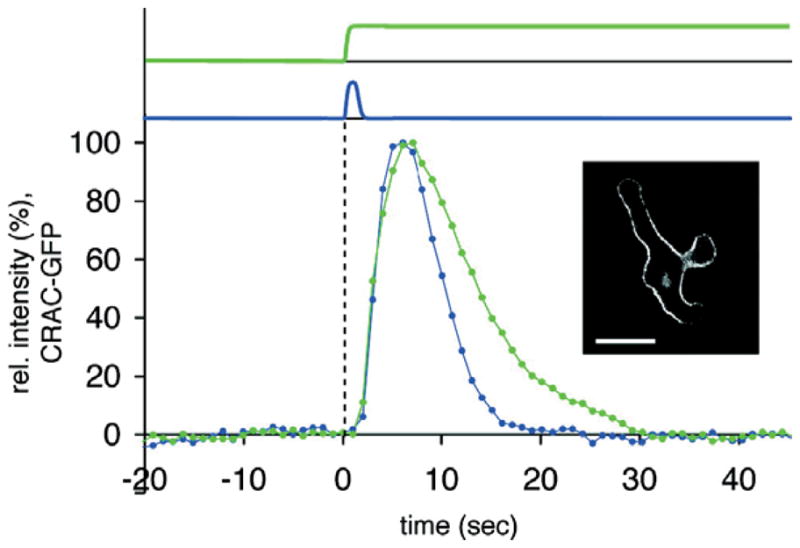
Translocation of CRAC-GFP in Dictyostelium cells in response to a short pulse (blue) and continuous (green) stimulation. Scale bar is 10 μm. (Reprinted with permission from Ref. ⁸⁸. Copyright 2007 American Chemical Society.)

To describe the mechanism of adaptation, two broad classes of models have been proposed and it is now known that these are the only two possible forms⁴². In the negative feedback loop model, the difference between the desired and achieved response is used to adjust upstream regulators, thus closing a negative feedback loop^{43, 44}. In the other class of model receptor occupancy drives two competing processes, a fast excitation and a slower inhibition. The balance of these competing processes sets the level of a response regulator⁴⁵. Because of the complementary regulation of the response regulator, this class of model is sometimes referred to as an incoherent feedforward loop (IFL)⁴⁶. However, in the context of amoeboid chemotaxis, the term local-excitation, global-inhibition (LEGI) is more commonly used^{5, 47, 48}. The terms “global” and “local” refer to the relative spatial distributions inside the cell; this distinction is only important when explaining the cellular response to chemoattractant gradients, as we will see below.

At the molecular level, studies using Forster resonance energy transfer (FRET) have demonstrated that under persistent stimulation, G-proteins associated with the chemoattractant receptor remain dissociated indicating that adaptation must take place at a point downstream of the receptor⁴⁹. One of the earliest signalling events is believed to be the activation of GTP-ase RasG^{50, 51}, which can be observed by tracking fluorescently tagged Ras-binding domain of human Raf1⁵². Upon stimulation using a microfluidic device, RasG activity displays an adaptive response⁵³. Fitting the data quantitatively to both classes of adaptation models showed that the LEGI-IFL model but not the negative feedback loop model could account for all the data⁵³. The RasGEF and RasGAP proteins that regulate GTP-ase activity fit the model requirements of the excitation and inhibition processes.

If RasG activation is the first, or one of the earliest adaptive steps, it is worth asking what happens downstream. Activation of Ras leads to increased PI3K activity, which can be observed by the translocation of PH-domain containing proteins to the newly formed PIP3 on the membrane^{40, 41, 54}. However, analysis of the response in individual cells has shown that it is only found in a fraction of cells, and that this fraction increases as the concentration of chemoattractant stimulus is raised⁵⁵. This behaviour is can be explained by a model in which the LEGI-IFL response feeds into a nonlinear circuit with a threshold if one assumes that the threshold value can vary from cell to cell⁵⁵. Thus, for a given stimulus level, some – but not all – thresholds are surpassed leading to a response. However, as the stimulus is raised, the fraction of cells that overcome the threshold and hence respond also increases.

The initial transient response of cells is not the only response elicited by chemoattractant stimuli. This is followed by a slower, more localized secondary phase of actin polymerization^56–59 and protein localization⁶⁰. During this time, cells are more likely to extend lateral pseudopods⁵⁸. Interestingly, the appearance of these secondary responses decreases in more polarized cells. Alone, none of the adaptation models can explain the presence of a biphasic response. However, if we consider a network whereby the LEGI-IFL model feeds into an excitable system, then biphasic responses appear¹². This topology is consistent with the presence of a threshold, which is supplied by the excitable system. Moreover, this model explains the presence of the cringe, which is a consequence of the refractory period of the excitable system. Though this model can explain the presence of a threshold and the biphasic response to uniform stimuli, it does mean that the time scale of adaptation must be slower than that of the excitable system. Thus, the first peak of activity and its return to basal level (approximately 20–30 seconds) is not a consequence of adaptation, but rather of the time that it takes the excitable system to complete one firing (Fig. 2b,c)¹². At this point, the system is only partially adapted. The secondary signs of activity are caused by further excitable firings induced by the partially adapted system upstream. Though these firings are fewer in number than the initial ones, wherever they occur, their level and duration is not dictated by the level of receptor occupancy¹⁰, but rather by the internal dynamics of the excitable system.

Response to chemoattractant gradients

That cells are able to sense gradients spatially can be seen in the response to chemoattractant gradients of cells treated by actin inhibitors such as latrunculin^{39, 61} (Fig. 5a). Following treatment, cells round up and display a relatively stable crescent in the direction of the gradient, allowing for careful quantification of the spatial response⁶¹ (Fig. 5a). The response is amplified meaning that the spatial gradient of internal markers is steeper than that of the chemoattractant⁶¹. This amplification is seen both in the presence and absence of an intact cytoskeleton, though it is larger in motile cells. A spatially dependent threshold is also observed. The level of the response follows not the absolute, but the relative chemoattractant gradient. Thus, cells are able to compare receptor occupancy throughout the whole membrane and respond only wherever local receptor exceeds the global mean. This echoes earlier findings that chemotaxis of cells is governed by the relative gradient⁶². Evidence for a threshold in directing migration has also been documented^{63, 64}.

Figure 5. Response to chemoattractant gradients.

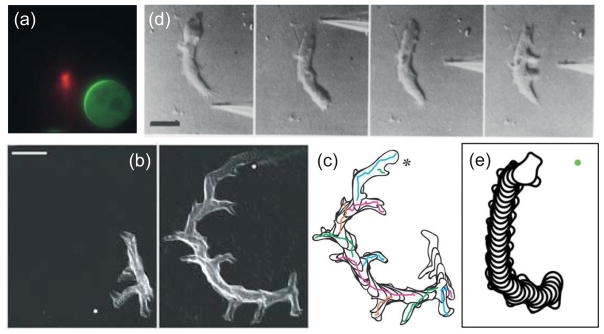
(a) Response of a latrunculin-treated Dictyostelium cell to a needle containing cy3-cAMP (red). The immobile cell forms a crescent of GFP-tagged PH-CRAC in the direction of highest concentration. (Reprinted with permission from Ref. ⁶¹. Copyright 2004 National Academy of Sciences USA.)(b,c) Overlays of a Dictyostelium cell chemotaxing to a cAMP-filled micropipette whose location (marked by the dot) is changed in the time between the two panels. The reorientation of the cell to the change in gradient, which is in the form of a gradual “u-turn” is seen in the overlay of the cell outlines in panel c. Scale bar is 20 μm. (Reprinted with permission from Ref. ²⁸. Copyright 2007 Nature Publishing Group.)(d) Reorientation of a Dictyostelium cell by a sufficiently strong change in gradient. Here, the pipette is first moved to the back which stops cytoplasmic flow at which point applying the needle to the side leads to the emergence of multiple pseudopodia. Scale bar is 10 μm. (Reprinted with permission from Ref. ⁷⁷. Copyright 1982 Elsevier Inc.)(e) Simulation showing the reorientation of a cell in response to a change in the direction of the chemoattractant gradient. (Reprinted with permission from Ref. ³⁴.)

The local-global comparison made by cells matches the predicted response of the LEGI mechanism⁶⁵. In this case, the excitation process is local. The inhibition process is created locally, but through diffusion becomes spatially global. The relative strengths of these two processes dictate the level of the response regulator. Thus, at the front, where excitation exceeds inhibition, it is above basal level. At the rear, where inhibition exceeds excitation, the response regulator is below basal levels⁴⁸. FRET studies have provided evidence for the local production of a local inhibitor upon chemoattractant stimulation⁶⁶.

On its own, the LEGI mechanism does not amplify gradients, so that a separate amplification step is needed. The fact that amplification is higher in cells with an intact cytoskeleton has led to suggestions that actin-dependent positive acts to amplify the signal. One possible feedback loop involves actin-dependent PI3K activation⁵¹. However, it is important to note that amplification is present in latrunculin-treated cells. Several schemes have been proposed, including switches^{48, 55, 67, 68}, built-in thresholds through the G-protein subunits⁶⁹, complementary regulation of enzymes⁶⁵, and the presence of an excitable network^{12, 29, 30, 34}. Amplification of the LEGI response regulation through an excitable system can recreate many of the observed responses. The excitable system provides the threshold that is observed under both spatially uniform stimuli and gradients. If the response regulator lowers the threshold at the front and raises it at the rear, then the likelihood of firings will increase in the direction of the gradient and be reduced at the rear. Thus, one might expect to see pseudopods only at the front.

Cells do not always respond in the direction of the highest receptor occupancy. Even in strong gradients, chemotactic cells show random fluctuations in the direction of their movement⁷⁰. In addition to this stochastic component, cells also acquire an intrinsic intracellular asymmetry that competes with the directional information provided by receptor occupancy^71–73. This asymmetry, or polarity, develops over time as cells move in a chemoattractant gradient. It can be seen in cell morphology – polarized cells become elongated – as well as in the spatial distribution of intracellular proteins. Some of these are relatively small – such as the spatial asymmetry displayed by G-protein subunits in highly polarized cells⁷⁴. Others are more pronounced; for example, PTEN is found only in a narrow region at the rear in polarized cells⁴⁰. Polarization also manifests itself in varying sensitivity to chemoattractant stimuli. This is best observed in cells exposed to a sudden change in the direction of the chemoattractant gradient. These cells gradually turn towards the new gradient while maintaining their axis of polarity^{28, 73, 75, 76} (Fig. 5b,c). Sufficiently strong gradients, however, can overcome this polarity^{37, 77} (Fig. 5d).

Polarization is believed to be the result of a stable breaking-of-symmetry brought about by positive feedback involving actin polymerization^{73, 78}. However, the spatial response of latrunculin-treated cells after stimulation by a gradient also shows cell-to-cell variability that is not the result of noise, since it is reproducible in any one cell ⁷⁹. This variability suggests that at least part of the intrinsic polarity mechanism is independent of actin polymerization.

How polarity fits into the excitable network hypothesis is unclear. It is likely that the mechanisms that ensure persistent motion in unstimulated cells may also be responsible for developing polarity in cells exposed to a stable gradient. Thus, cells would retain a memory of the existing pseudopod location and use this signal to reinforce the likelihood of future pseudopods appearing in that direction, by effectively reducing the threshold of the excitable system at that location. At the same time, inhibiting activity of the excitable system elsewhere in the cell makes lateral pseudopods less likely. Models describing this complementary regulation do turn in response to changes in the direction of the gradient³⁴ (Fig. 5e). It has also been suggested that because polarization induces changes in cellular morphology, the signalling by proteins shuttling to and from the membrane is affected⁸⁰.

Conclusion

The hypothesis that an excitable system regulates chemoattractant-mediated signalling and actin polymerization in amoeboid cells has enabled researchers to explain many cellular observed behaviours, both at the whole-cell scale, such as the stochastic nature of the cellular movement, as well as more local responses, such as protein localization at tips of protrusions or the morphology of splitting pseudopods. Moreover, if we assume that chemoattractant receptor occupancy biases the likelihood that this excitable behaviour is triggered by selectively altering the threshold of activation (lowering it at the front and raising it at the rear), then a number of other observations can also be explained, including the gradient-dependent chemotactic index observed in cell trajectories. To date, however, no model is able to explain all the data – biochemical, morphological and at the whole cell level – to the different combinations of stimuli – spatially uniform, gradients, or unstimulated cells.

One of the characteristics of excitable systems is that they operate at a single stable equilibrium. However, small changes in the parameter can change the stability, or even the number of equilibria, leading to oscillatory or bistable systems. There are indeed suggestions that, under certain conditions, such changes are observed in Dictyostelium where bistable⁸¹ and oscillatory¹³ behaviour is observed. A model, based on actin-mediated feedback, has been proposed that explains the transition between different experimentally observed patterns of activity⁸².

At present, our molecular understanding of how the excitable system operates is lacking. Clearly, a number of feedback loops, both positive and negative, need to be accounted for. For example, to have the excitable behaviour we must have an autocatalytic positive feedback loop. Reports suggest that this could come about from the actin cytoskeleton through Ras and PI3K⁸³. Alternatively, positive feedback could be at the cytoskeletal level alone mediated by actin-dependent Arp2/3 nucleation⁸⁴. Mathematical models of excitable behaviour point to the fact that the system is extremely sensitive to the strength of this feedback loop¹². How cells could manage this sensitivity is unclear. The excitable system hypothesis also requires a number of negative feedback loops with differing spatial characteristics, some local, some global^{5, 29, 31, 34}. It has been suggested that some of this feedback could be achieved through the mechanical properties of cells⁸⁵, with membrane⁸⁶ or cortical tension⁸⁷ providing some of the inhibitory activity.

The recent progress in understanding chemotaxis in eukaryotic cells has been possible because of the combination of live-cell imaging, novel image analysis tools, new experimental techniques such as microfluidic chambers, and the use of mathematical models to test hypotheses. It is integration of these various scientific fields that lies in the heart of systems biology and that will allow chemotaxis research to continue to move forward.