Figure 2. Cluster-based statistics of correlation coefficients for multiple comparison correction.

The first step generates N permutation vectors by randomly reordering behavioral scores (the upper-left corner). Suppose there are n subjects in the given group. Then, the ith permutation vector PV _i, i = 1,2,…,N, has n elements, the ordering of n subjects’ behavioral scores. Note that the last permutation vector PV _N is constructed using the original ordering of the behavioral scores as usual in any permutation testing. We compute a partial correlation coefficient between an edge and the behavioral scores for every permutation vector. We repeat this procedure for every edge, resulting 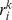, i = 1,2,…,N and k = 1,2,…,m, where m is the total number of edges (the upper middle). In the second step, we extract sets of network edges of which correlation coefficient is beyond the initial threshold to form supra-threshold clusters. Denoted by the resulting cluster is corresponding to the jth cluster of the ith permutation vector PV _i, i = 1,2,…,N and j = 1,2,…c_i, where c_i is the number of identified clusters for PV _i. For a positive initial threshold, edges whose correlations were larger than it will form clusters, while for a negative threshold edges whose correlation is smaller than it will do. We employ the maximum cluster extent for the null permutation distribution by counting the number of edges in the largest connected sub-network of each permutation. 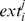represents the number of edges in 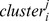, and 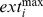represents the maximum cluster extent for PV _i (the upper-right corner)_. This representative statistic forms a null permutation distribution, which is shown as the histogram (the bottom). Finally, we estimate the significance level over the null distribution by computing the proportion of the number of entries whose maximal cluster extents are larger than the size of each identified sub-network, , (black entries in the histogram) to the number of entries, N.