Abstract
We survey thermodynamic measurements on processes involving biological macromolecules in aqueous solution, which illustrate well the ubiquitous phenomenon of entropy-enthalpy compensation. The processes include protein folding/unfolding and ligand binding/unbinding, with compensation temperatures varying by about 50 K around an average near 293 K. We show that incorporating both near-exact entropy-enthalpy compensation (due to solvent relaxation) and multi-excitation entropy (from vibrational quanta) leads to a compensation temperature in water of about 230 K. We illustrate a general procedure for subtracting solvent and environment-related terms to determine the bare Gibbs free energy changes of chemical processes.
Keywords: Macromolecules, Biological macromolecules, Entropy-enthalpy compensation, Hydrophobic interactions
Introduction
In the last couple of decades, significant progress has been made in understanding temperature-dependence of the specific interactions among various functional biological macromolecules or between biomacromolecules and an array of small ligands of different sizes, charges and interaction affinities. These efforts contributed to accumulation of a substantial amount of thermodynamic parameters that feature these weak interactions in biological systems. In general, the thermodynamic parameters of these molecular biosystems in aqueous phase are derived from equilibrium constant recordings at different temperatures (e.g., either association, Ka, or dissociation constant, Kd) and semi-log Van 't Hoff plots (1). In many examples, the temperature dependence of biomolecular interactions reveals a phenomenon called enthalpy-entropy compensation (EEC) (2–7).
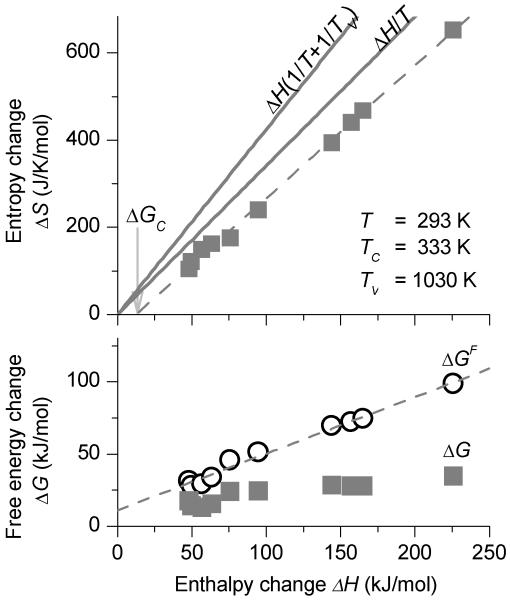
The phenomena of EEC are illustrated in Fig. 1. In the upper panel, the solid squares indicate measurements of the standard entropy and enthalpy changes associated with imino proton exchange in the particular basepairs in RNA (8). As can be seen, there is a linear trend of these data with a positive slope, which is the compensation effect. Each individual basepair's entropy and enthalpy change can be denoted ΔSi and ΔHi. The series of measurements is evidently fitted well by a linear relationship:
| (1) |
where we denote the intercept of the fitting line on the enthalpy axis as the compensation free-energy ΔGC, and the reciprocal slope of the plot as the compensation temperature TC. The lower panel of Fig. 1 illustrates the Gibbs free energy measurements of the same series. The magnitudes of the free energies are significantly smaller than the enthalpies, which indicates that there is significant compensation of the terms ΔH and TΔS in the expression ΔG ≡ ΔH – TΔS. This is anticipated when the compensation temperature TC is reasonably close to the experimental temperature T, as was true for these measurements.
Figure 1.
(upper) The symbols are measurements of entropy change and enthalpy change for imino proton exchange for several basepairs in RNA. The dashed fitting line yields the compensation temperature TC and free energy ΔGC for the measurements. The line labeled ΔH/T shows exact compensation; the line labeled ΔH/(1/T + 1/TV) shows the effects of water's structural relaxation and vibrational quantization (multi-excitation entropy). (lower) The solid symbols show Gibbs free energy measurements on the base pairs ΔGi. The open symbols show the free energies after correction for water's structural relaxation and vibrational quantization.
There are two very general models that have been proposed to explain the ubiquity of EEC for macromolecules in water. First, the hydrophobic and hydrogen bonding interactions between the water and the macromolecules lead to large associated entropy and enthalpy terms. Ben-Naim suggested the colorful distinction between the entropy and enthalpy changes when the structure of the water is “frozen”, and the changes incorporating the “relaxation” of the water. Several papers in the last decades have concluded that these relaxation enthalpy and entropy terms compensate perfectly compensate each other; the line labeled ΔH/T illustrates this relationship; this perspective has been reviewed by some of its originators in Ref. (5;9;10). This “near-exact” compensation effect applies in all solvents, but is particularly significant for water.
The second general effect is the entropy associated with the quantization of vibrations in the solvent, which can be inferred from vibrational spectroscopy of the solvent. This “multi-excitation entropy” effect leads to an entropy compensation temperature TV that applies to all the enthalpy of a macromolecular process, and not just to the solvent relaxation enthalpy. This effect has been reviewed by some of its proponents in Ref. (6;11).
In addition to these general effects, each individual macromolecular system may have additional internal compensation terms. However, it is not known whether or how these various compensation effects should add together to determine the final entropy-enthalpy relationship of a system of macromolecules, nor is a procedure established for parsing an individual set of measurements such as that in Fig. 1 to determine the relative contributions of the several effects.
Results and Discussion
Survey of EEC compensation for biological macromolecules in water
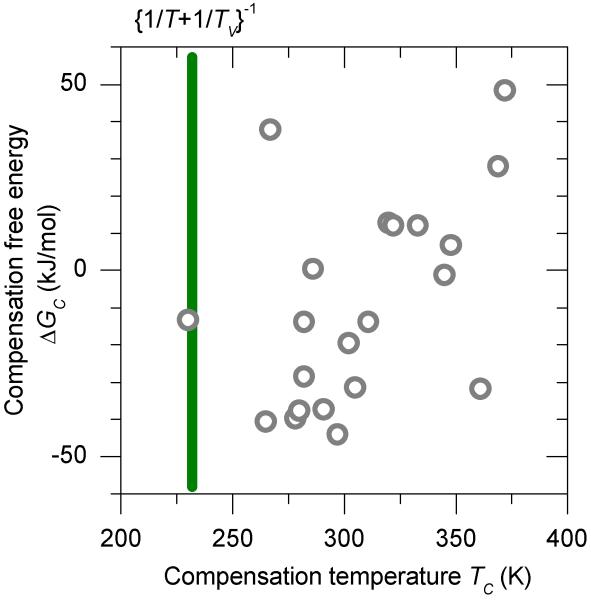
We have collected experimental estimates for the compensation temperature TC and the compensation free energy change ΔGC in Table 1. The compensation temperatures, TC, are clustered around 293 K, which is the typical measurement temperature. There are many deviations from this temperature point that will be discussed below. The Gibbs compensation free energy ΔGC has values in the range −44 to 58 kJ/mol.
Table 1.
Compensation temperatures and the Gibbs free energies at the compensation temperature for various chemical and biophysical systems
| TC (K) | kJ/mol | System | Experimental Approach | Reference |
|---|---|---|---|---|
| 278 | −39.9 | drug-protein receptor binding interactions | Temperature dependence of association constants | Gilli et al. (16) |
| 305 | −31.5 | DNA-transcriptional factor interactions | analytical laser scattering (ALS) in combination with isothermal titration calorimetry (ITC) | Seldeen et al., 2009 (17) and Starikov and Nordén, 2012 (18) |
| 291 | −37.4 | DNA-transcriptional factor interactions | analytical laser scattering (ALS) in combination with isothermal titration calorimetry (ITC) | Seldeen et al., 2009 (51) and Starikov and Nordén, 2012 (18) |
| 282 | −28.6 | DNA-drug interactions | Combination of spectroscopic and calorimetric techniques | Starikov and Norden, 2007 (7) |
| 361 | −31.9 | DNA-drug interactions | Combination of spectroscopic and calorimetric techniques | Starikov and Nordén, 2007 (7) |
| 280 | −37.8 | Calcium binding | Calorimetry | Kuroki and colleagues (52) and Sharp, 2001 (48) |
| 286 | 0.4 | Small globular protein unfolding | Calorimetry | Sharp, 2001 (48) |
| 267 | 37.8 | Unfolding of large proteins | Hydrogen exchange protection factors | Sharp, 2001 (48) |
| 282 | −13.9 | Host-guest complexes of cyclodextrins | Calorimetry | Houk et al., 2003 (53) |
| 311 | −13.9 | Host-guest complexes of non-cyclodextrins | Calorimetry | Houk et al., 2003 (53) |
| 230 | −13.4 | Host-guest complexes in non-aqueous solution | Calorimetry | Houk et al., 2003 (53) |
| 297 | −44.1 | Antibody-antigen complexes of proteins and carbohydrates | Calorimetry | Houk et al., 2003 (53) |
| 320 | 12.6 | Thermally induced unfolding in globular proteins | Two-state analysis of differential scanning calorimetry (DSC) | Cooper et al., 2001 (28) |
| 322 | 12 | DNA base-pair opening | NMR spectroscopy coupled with temperature dependence of imino proton exchange rates | Steinert et al., 2012 (8) |
| 333 | 12 | RNA base-pair opening | NMR spectroscopy coupled with temperature dependence of imino proton exchange rates | Steinert et al., 2012 (8) |
| 372 | 48.3 | Melting of DNA duplex | Differential scanning calorimetry | Steinert et al., 2012 (54) |
| 369 | 27.9 | Ligand-receptor interactions | Competitive peptide binding assay | Ferrante and Gorski, 2012 (29) |
| 265 | −40.6 | Drug-membrane protein receptor interactions | Calorimetry | Grunwald and Steel, 1995 (9) |
| 302 | −19.7 | Thermodynamic properties of micellization of Sulfobetaine-type Zwitterionic Gemini Surfactants in aqueous solutions | A free energy perturbation study | Liu et al., 2012 (55) |
| 345 | −1.3 | Melting of nucleic acids Poly(dA-dT)·poly(dA-dT) | Differential Raman spectroscopy | Movileanu, et al. 2002 (1) |
| 348 | 6.7 | Melting of nucleic acids Poly(dA)·poly(dT) | Differential Raman spectroscopy | Movileanu, et al., 2002 (1) |
Before commenting on some of the individual entries in the table, we note a general issues regarding the parameter estimates. Pioneering work of Krug and collaborators (12;13) showed that a linear relationship between enthalpy and entropy differences is sensitive to the correlation of the statistical errors when the differences are derived from van 't Hoff analyses (enthalpy obtained from a graph of the equilibrium constant vs. reciprocal temperature). Recently, Starikov and Norden (14) has emphasized that entropy-enthalpy relations based on calorimetric measurements are relatively insensitive to this problem. We have identified the measurement techniques in Table I. We have not otherwise discriminated against estimates for TC and ΔGC based on van `t Hoff analyses, which can be valid when errors are sufficiently small (3;15).
Gilli and colleagues (1994) have compiled ligand (drug) binding experiments for thirteen macromolecule systems including ten biological receptors (16). A linear regression of the scatter plot between the standard enthalpies and entropies provided a compensation temperature of 278 ± 4 K and a free energy of interaction at the compensation temperature of −39.9 ± 0.9 kJ/mol (16). Values of ΔH° and ΔS° were obtained from Van 't Hoff plots of the drug-receptor binding equilibrium curves, which were linear in the temperature range 273 – 310 K.
The data analysis of thermodynamic parameters ΔH° and ΔS° was applied to the system DNA binding site TGACGTCA – bZIP domain in Jun transcription factor (17). Methodical modifications of the sequence of the DNA binding revealed EEC with ΔGC = −3.15 kJ/mol (18). In contrast, systematic alterations in the length of the binding protein (bZIP domain) resulted in an EEC signature with a compensation temperature of 291 K and ΔGC = −37.4 kJ/mol.
We also show an example related to the thermostability of double-stranded DNA (dsDNA) and double-stranded RNA (dsRNA) oligonucleotides. Individual base-pair stability of dsDNA and dsRNA was pursued using optimized NMR methodology (8). Steinert and colleagues (2012) (8) found that the compensation temperature, Tc, for short dsDNA and dsRNA oligonucleotides is 322 and 333 K, respectively. Remarkably, this coincides with the melting temperature of the two double-stranded oligonucleotides (Table 1).
Differential Raman spectroscopy (19;20) and Van 't Hoff plots (1) were employed to examine the structural alterations and thermodynamics of the premelting and melting transitions in long dsDNA polymers poly(dA-dT)·poly(dA-dT) and poly(dA)·poly(dT). Similar to Steinert and colleagues' study (8), the compensation temperature of these polynucleotides was 345 and 348 K (Table 1), respectively, which was very close to the melting temperature, Tm, of these biopolymers of 344 and 349 K, respectively.
EEC was found in the energetics of protein folding and stability (2;4;21;22). EEC is one of the most puzzling process in molecular recognition employing a folded protein and a ligand (23–25). Dunitz (1995) has hypothesized that enthalpically more favorable binding interactions between a ligand and a protein would result in a greater restriction of the moieties, so more entropy adverse (26). However, we think that more than a single mechanism is involved in the EEC process in a biomolecular system in aqueous phase, such as the role of cosolutes and osmotic stress, the solvation and water orientation as well as the dynamics of water binding to the polypeptide side chains, hydrophobic hindrance, and so on (24;27–29). Therefore, a defragmentation of the EEC quantitative data in components reflecting each contributing mechanism is an intimidating and persistent challenge. In addition, the protein systems in aqueous phase experience a variety of conformational transitions leading even to negative activation enthalpies (30–32), which certainly requires compensatory negative activation entropies.
General mechanisms for EEC and near-exact EEC
We briefly describe two rather general mechanisms for EEC involving a macromolecule in water (3;6), and then we'll discuss the particular subset of compensation temperatures shown in Fig. 2. We shall call the first mechanism “near-exact entropy enthalpy compensation”, which we'll denote eEEC. Near-exact compensation implies that ΔS ≈ ΔH/T, and thus implicitly that the Gibbs free energy ΔG ≡ ΔH – TΔS is much smaller than the enthalpy (ΔG ⪡ ΔH). The second mechanism has been called “multi-excitation entropy”, which we'll denote MEE. MEE roughly implies that ΔS = ΔH/TV. TV is a temperature largely determined by the vibrational frequency spectrum of the solvent or matrix; in the case of a narrow spectrum centered at optical frequency ω0, TV ≈ ℏω0/KB, where ℏ and KB are Planck's and Boltzmann's constants, respectively. In this paper, we only summarize these results; there have been several comprehensive reviews that should be consulted for a discussion of the underlying theories (3;6;9;11).
Figure 2.
Two-dimensional scatter plot of the compensation temperatures and Gibbs compensation free energies for some biomolecular systems in aqueous phase. See Table I for details. The vertical line at 235 K indicates the compensation temperature that is predicted from the properties of water, and neglecting the internal entropy and enthalpy changes of the macromolecule systems.
Several authors have recognized the possibility of near-exact entropy-enthalpy compensation (eEEC) in solvents such as water with structure that “relaxes” around a solute molecule, and we would anticipate that these effects would be especially significant for macromolecules in aqueous solution. The effect can be strong, and can be thought of as a change in the entropy ΔSR associated with the water surrounding the solute molecules. This relaxation entropy is exactly compensated by a corresponding relaxation enthalpy: ΔHR = TΔSR (5;9;10).
Because of this exact compensation, these large relaxation effects do not affect the chemical potential for processes such as solvation. Ben-Naim (10), Grunwald (9), Yu and Karplus (33), and Qian and Hopfield (5) have all given related arguments. They are rather general, and apply to localized processes (solvation, ligand binding, protein folding/unfolding, etc.) embedded in any matrix with relaxation enthalpies significantly larger than the Gibbs free-energy of the process. After Ben-Naim, we write:
| (2) |
and are the measured enthalpy and entropy change for some process i, and incorporate the relaxation enthalpy and entropy as well as “frozen-state” terms neglecting relaxation:
| (3a) |
| (3b) |
where and are the frozen state entropy and enthalpy. is the Gibbs free energy of the process, which is unaffected by relaxation because of the exact compensation effect. Now consider a collection of related processes i such as a particular ligand that binds and unbinds to a series of related macromolecules. The varying macromolecules will each have different, but compensating relaxation entropy and enthalpy changes and .
Presuming that is small compared to , the usual expression:
| (4) |
implies that a scatter plot of and will cluster around the line TΔS = ΔH, with small deviations . The key feature of eEEC is that the compensation temperature should be the same as the temperature of the measurement.
The multi-excitation entropy mechanism for EEC
The second EEC mechanism that we'll consider is “multi-excitation entropy” (MEE). Several authors (Peacock-Lopez, Suhl, Linert, Khait, Yelon, and Movaghar) proposed related ideas in the 1980s (11;34–37). MEE amounts to an additional entropy change from annihilation of the several vibrational quanta needed to excite a process i over its enthalpy barrier. These can be associated with an additional entropy term , where TV ≈ ℏω0/kB is determined by a characteristic vibrational frequency ω0 of the matrix or solvent. Theoretically, for a system with a well-defined Einstein mode, we anticipate proportionality as long as (i) TV is significantly greater than T, and (ii) the enthalpy barrier is significantly greater thanℏ the latter is the “multi-excitation” criterion. (6)
When both are present, the relaxation and MEE entropies add. We write:
| (5) |
This equation is the main tool we use to parse the relative effects of the internal and solvent-related entropies and enthalpies for a series of macromolecule processes. Note that, although the entropy is changed by the MEE term, the enthalpy is not affected. This expression yields the “frozen” free energy from the enthalpy and entropy measurements, presuming that TV can be estimated.
If we presume the first term on the right of eq. (5) is small compared to the second, then the compensation temperature TS associated solely with solvent effects is reduced somewhat from its near-exact value according to:
| (6) |
This equation incorporates eEEC as the limit with large TV, and it also indicates that systems with substantial relaxation (such as aqueous solutions) are not ideal for the observation of MEE. A clear demonstration of MEE requires compensation temperatures exceeding T significantly, but near-exact compensation generally keeps compensation temperatures below T.
Application to biological macromolecules in water
We can adapt the discussion of the previous section and offer the following perspective on the compensation temperatures summarized in Fig. 2. We think that the near-exact EEC model is likely the best starting point for explaining the otherwise remarkable coincidence that a wide range of experiments on macromolecules in aqueous solution yield a compensation temperature near the measurement temperature. In addition to the near congruence of the measurement and compensation temperatures, for each of the experiments summarized in Fig. 2, the Gibbs free energies were much smaller than the range of enthalpies, which is the second criterion for eEEC as the primary origin of compensation.
The eEEC model is plainly incomplete. As Fig. 2 shows, there is a significant range of compensation temperatures around the value of 295 K, and the eEEC model is silent on this. The MEE model also fails to account for this variability; the MEE model's strength is that it accounts for variation in the compensation temperatures for solvents and matrices with varying vibrational spectra. All of these experiments were done in aqueous solution. We argue that the joint effect of eEEC and MEE is to predict a single compensation temperature for aqueous systems that is significantly lower the measurement temperature.
Experimentally (6), there is a fair proportionality between measurements of “isokinetic” temperatures and characteristic vibrational frequencies (determined spectroscopically) for numerous physical systems ranging from electron trapping and defect annealing in semiconductors to chemical reactions in a wide range of solvents or solid surfaces. The isokinetic temperature is analogous to compensation temperature for EEC, but applies to kinetic measurements instead of equilibrium measurements. The two temperatures need not be identical (38), although one survey that compared their values concludes that they were close (39).
As a provisional measure, we assume that TV is the isokinetic temperature of about 1.0 × 103 that corresponds to the vibrational band of water at 700 cm−1 (11). The predicted compensation temperature for measurements near 293 K is then TS = 0.23 × 103 K, which was used in preparing Fig. 1.
This “eEEC+MEE” compensation temperature will not vary for the different macromolecule systems, and thus cannot explain the spread of the measurements in Fig. 2. Beyond these two models, each individual system of molecules will have some relationship of the remaining entropy & enthalpy terms that depend on the details of the macromolecule system. In Fig. 1, we illustrate the “frozen-in” Gibbs free energy change for an RNA/solvent exchange measurement. As can be seen, there is a good linear dependence of this free energy upon the measured enthalpy change of the system. Note that the latter includes the solvent relaxation enthalpy.
Internal entropy-enthalpy compensation in biomacromolecules
Internal entropy and enthalpy changes needn't yield a linear EEC relation. This point has been emphasized by Ford (40), who did calculations of entropies and enthalpies for gas-phase dissociation models, and found compensation, anticompensation, and ill-behaved relationships. However, as summarized in Fig. 2, most biomolecular systems in aqueous phase do exhibit normal compensation. Eq. (5) indicates that this should happen as long as there is a reasonable linear relationship of the internal free energies to the total enthalpy ; the fact that compensation temperatures exceed 230 K indicates that the slope of this relationship is positive.
Many authors have suggested entropy-enthalpy models that are specific to the individual macromolecular systems under study. We briefly summarize some of these. At present, none of them enable us to predict the increase of the compensation temperature above 230 K for a particular system.
Liu and Guo (3) published a comprehensive review of EEC that discusses a perspective originally advanced by Larsson (41). For the biomolecules we are discussing, this perspective emphasizes the vibrational properties of the solute macromolecule itself. This seems entirely plausible for macromolecules in solution, and might account broadly for the range of compensation temperatures in Fig. 2.
Another intriguing idea has been advanced in several papers by Starikov and Nordén, who rationalize EEC data in terms of a micro-phase transition (MPT) (14;18). Starikov and Nordén explained that modifications of the nucleotide sequence of the DNA binding site corresponded to an “imaginary artificial heat pump,” whereas the changes of the binding polypeptide chain, which also involved changes in electrostatics, represented a “imaginary artificial refrigerator,” accounting for an equivalent Carnot cycle of the MPT (18). In this respect it is interesting that both the eEEC and MEE models lead to entropy changes that are proportional to the enthalpy change. Such proportionality doesn't account for a non-zero free-energy intercept ΔGC (see figures). Starikov and Nordén have emphasized that the Carnot interpretation involves energies such as ΔGC, which are apparently true internal properties of the embedded chemical process.
We note that entropy-enthalpy compensation is involved in measurement of the “temperature factor” of a protein, Q10, which is defined as a ratio between the kinetic rate constant at the absolute temperature T + 10 K and the same kinetic rate constant at T. Values are typically between 2–6 (42–46), which requires an activation enthalpy that is much greater than the thermal energy factor kBT. Large enthalpic contributions (ΔH≠) to the transition state energies would imply that these transitions would never be observable or would have a very low probability. Therefore, these enthalpic contributions have to be compensated by large entropic contributions (ΔS≠) to drastically reduce the activation free energies (ΔG≠) required for such conformational transitions in proteins and other biopolymers (42).
In the most simplistic reasoning, the breaking of inter- and intra-molecular bonds, either covalent or non-covalent, in a biomolecular system in aqueous phase, which includes the molecules under investigation as well as the solvent, will be an endothermic process. This is indicated by an increase in the standard enthalpy, ΔH° (it is a positive parameter). Intuitively, this is accompanied by an enhancement in the molecular mobility and backbone flexibility of the participating molecules, which would result in a greater standard entropy ΔS° (it is a positive parameter) (9;47). The compensatory nature of these thermodynamic parameters means that the absolute values of these parameters cannot be employed as a diagnostic of a particular biomolecular interaction (48;49). Large compensatory values of ΔH° and ΔS° produce a small value of ΔG°, a parameter that characterizes the functionality of a biomolecular system in aqueous phase (50).
Acknowledgments
The authors thank Arthur Yelon (École Polytechnique de Montréal) for Meyer-Neldel discussions over some years and for a critical reading of the manuscript. LM's research has been funded in part by grants from the US National Science Foundation (DMR-1006332) and the National Institutes of Health (R01 GM088403).
References
- 1.Movileanu L, Benevides JM, Thomas GJ. Determination of base and backbone contributions to the thermodynamics of premelting and melting transitions in B DNA. Nucleic Acids Res. 2002;30:3767–3777. doi: 10.1093/nar/gkf471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lumry R, Rajender S. Enthalpy-Entropy Compensation Phenomena in Water Solutions of Proteins and Small Molecules - A Ubiquitous Property of Water. Biopolymers. 1970;9:1125. doi: 10.1002/bip.1970.360091002. [DOI] [PubMed] [Google Scholar]
- 3.Liu L, Guo QX. Isokinetic relationship, isoequilibrium relationship, and enthalpy-entropy compensation. Chem. Rev. 2001;101:673–695. doi: 10.1021/cr990416z. [DOI] [PubMed] [Google Scholar]
- 4.Lumry R. Uses of enthalpy-entropy compensation in protein research. Biophys. Chem. 2003;105:545–557. doi: 10.1016/s0301-4622(03)00065-6. [DOI] [PubMed] [Google Scholar]
- 5.Qian H, Hopfield JJ. Entropy-enthalpy compensation: perturbation and relaxation in thermodynamic systems. J. Phys. Chem. 1996;105:9292–9298. [Google Scholar]
- 6.Yelon A, Movaghar B, Crandall RS. Multi-excitation entropy: its role in thermodynamics and kinetics. Reports on Progress in Physics. 2006;69:1145–1194. [Google Scholar]
- 7.Starikov EB, Norden B. Enthalpy-entropy compensation: a phantom or something useful? J. Phys. Chem. B. 2007;111:14431–14435. doi: 10.1021/jp075784i. [DOI] [PubMed] [Google Scholar]
- 8.Steinert HS, Rinnenthal J, Schwalbe H. Individual Basepair Stability of DNA and RNA Studied by NMR-Detected Solvent Exchange. Biophys. J. 2012;102:2564–2574. doi: 10.1016/j.bpj.2012.03.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Grunwald E, Steel C. Solvent Reorganization and Thermodynamic Enthalpy-Entropy Compensation. Journal of the American Chemical Society. 1995;117:5687–5692. [Google Scholar]
- 10.Ben-Naim A. Molecular Theory of Water and Aqueous Solutions - Part I: Understanding Water World Scientific. Singapore: 2009. [Google Scholar]
- 11.Linert W, Jameson RF. The Isokinetic Relationship. Chemical Society Reviews. 1989;18:477–505. [Google Scholar]
- 12.Krug RR, Hunter WG, Grieger RA. Enthalpy-Entropy Compensation .1. Some Fundamental Statistical Problems Associated with Analysis of Vant Hoff and Arrhenius Data. Journal of Physical Chemistry. 1976;80:2335–2341. [Google Scholar]
- 13.Krug RR, Hunter WG, Grieger RA. Statistical Interpretation of Enthalpy-Entropy Compensation. Nature. 1976;261:566–567. [Google Scholar]
- 14.Starikov EB, Norden B. Entropy-enthalpy compensation as a fundamental concept and analysis tool for systematical experimental data. Chemical Physics Letters. 2012;538:118–120. [Google Scholar]
- 15.Krug RR, Hunter WG, Grieger RA. Enthalpy-Entropy Compensation .2. Separation of Chemical from Statistical Effect. Journal of Physical Chemistry. 1976;80:2341–2351. [Google Scholar]
- 16.Gilli P, Ferretti V, Gilli G, Borea PA. Enthalpy-Entropy Compensation in Drug-Receptor Binding. Journal of Physical Chemistry. 1994;98:1515–1518. [Google Scholar]
- 17.Seldeen KL, McDonald CB, Deegan BJ, Bhat V, Farooq A. DNA plasticity is a key determinant of the energetics of binding of Jun-Fos heterodimeric transcription factor to genetic variants of TGACGTCA motif. Biochemistry. 2009;48:12213–12222. doi: 10.1021/bi901392k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Starikov EB, Norden B. Entropy-enthalpy compensation may be a useful interpretation tool for complex systems like protein-DNA complexes: An appeal to experimentalists. Applied Physics Letters. 2012;100 [Google Scholar]
- 19.Movileanu L, Benevides JM, Thomas GJ. Temperature dependence of the Raman spectrum of DNA. Part I - Raman signatures of premelting and melting transitions of poly(dA-dT)center dot poly(dA-dT) J. Raman Spectrosc. 1999;30:637–649. doi: 10.1002/bip.10022. [DOI] [PubMed] [Google Scholar]
- 20.Movileanu L, Benevides JM, Thomas GJ. Temperature dependence of the Raman spectrum of DNA. II. Raman signatures of premelting and melting transitions of poly(dA)- poly(dT) and comparison with poly(dA-dT)-poly(dA-dT) Biopolymers. 2002;63:181–194. doi: 10.1002/bip.10022. [DOI] [PubMed] [Google Scholar]
- 21.Liu L, Yang C, Guo QX. A study on the enthalpy-entropy compensation in protein unfolding. Biophys. Chem. 2000;84:239–251. doi: 10.1016/s0301-4622(00)00130-7. [DOI] [PubMed] [Google Scholar]
- 22.Blasie CA, Berg JM. Entropy-enthalpy compensation in ionic interactions probed in a zinc finger peptide. Biochemistry. 2004;43:10600–10604. doi: 10.1021/bi0363230. [DOI] [PubMed] [Google Scholar]
- 23.Raffa RB. (Extra)thermodynamics of the drug-receptor interaction. Life Sci. 1999;65:967–980. doi: 10.1016/s0024-3205(99)00197-6. [DOI] [PubMed] [Google Scholar]
- 24.Whitesides GM, Krishnamurthy VM. Designing ligands to bind proteins. Q. Rev. Biophys. 2005;38:385–395. doi: 10.1017/S0033583506004240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Marshall GR, Feng JA, Kuster DJ. Back to the future: ribonuclease A. Biopolymers. 2008;90:259–277. doi: 10.1002/bip.20845. [DOI] [PubMed] [Google Scholar]
- 26.Dunitz JD. Win some, lose some: enthalpy-entropy compensation in weak intermolecular interactions. Chem. Biol. 1995;2:709–712. doi: 10.1016/1074-5521(95)90097-7. [DOI] [PubMed] [Google Scholar]
- 27.Qian H, Chan SI. Interactions between a helical residue and tertiary structures: helix propensities in small peptides and in native proteins. J. Mol. Biol. 1996;261:279–288. doi: 10.1006/jmbi.1996.0459. [DOI] [PubMed] [Google Scholar]
- 28.Cooper A, Johnson CM, Lakey JH, Nollmann M. Heat does not come in different colours: entropy-enthalpy compensation, free energy windows, quantum confinement, pressure perturbation calorimetry, solvation and the multiple causes of heat capacity effects in biomolecular interactions. Biophysical Chemistry. 2001;93:215–230. doi: 10.1016/s0301-4622(01)00222-8. [DOI] [PubMed] [Google Scholar]
- 29.Ferrante A, Gorski J. Enthalpy-entropy compensation and cooperativity as thermodynamic epiphenomena of structural flexibility in ligand-receptor interactions. J. Mol. Biol. 2012;417:454–467. doi: 10.1016/j.jmb.2012.01.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Oliveberg M, Tan YJ, Fersht AR. Negative activation enthalpies in the kinetics of protein folding. Proc. Natl. Acad. Sci. U. S. A. 1995;92:8926–8929. doi: 10.1073/pnas.92.19.8926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Noronha M, Gerbelova H, Faria TQ, Lund DN, Smith DA, Santos H, Macanita AL. Thermal unfolding kinetics of ubiquitin in the microsecond-to-second time range probed by Tyr-59 fluorescence. J. Phys. Chem. B. 2010;114:9912–9919. doi: 10.1021/jp104167h. [DOI] [PubMed] [Google Scholar]
- 32.Cheneke BR, Indic M, van den Berg B, Movileanu L. An Outer Membrane Protein undergoes Enthalpy- and Entropy-driven Transitions. Biochemistry. 2012;51:5348–5358. doi: 10.1021/bi300332z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Yu HA, Karplus M. A Thermodynamic Analysis of Solvation. Journal of Chemical Physics. 1988;89:2366–2379. [Google Scholar]
- 34.Peacock-Lopez E, Suhl H. Compensation Effect in Thermally Activated Processes. Physical Review B. 1982;26:3774–3782. [Google Scholar]
- 35.Khait YL. Kinetic Many-Body Theory of Short-Lived Large Energy Fluctuations of Small Numbers of Particles in Solids and Its Applications. Physics Reports-Review Section of Physics Letters. 1983;99:239–340. [Google Scholar]
- 36.Yelon A, Movaghar B. Microscopic Explanation of the Compensation (Meyer-Neldel) Rule. Physical Review Letters. 1990;65:618–620. doi: 10.1103/PhysRevLett.65.618. [DOI] [PubMed] [Google Scholar]
- 37.Yelon A, Movaghar B, Branz HM. Origin and Consequences of the Compensation (Meyer-Neldel) Law. Physical Review B. 1992;46:12244–12250. doi: 10.1103/physrevb.46.12244. [DOI] [PubMed] [Google Scholar]
- 38.Yelon A, Sacher E, Linert W. Multi-Excitation Entropy, Entropy-Enthalpy Relations, and their Impact on Catalysis. Catalysis Letters. 2011;141:954–957. [Google Scholar]
- 39.Linert W. Concerning the Problem of the Isokinetic Relationship .4. the Evaluation of the Isosubstituent Hammett Parameter by Means of Isokinetic and Isoequilibrium Temperatures. Australian Journal of Chemistry. 1986;39:199–208. [Google Scholar]
- 40.Ford DM. Enthalpy-entropy compensation is not a general feature of weak association. J. Am. Chem. Soc. 2005;127:16167–16170. doi: 10.1021/ja054519c. [DOI] [PubMed] [Google Scholar]
- 41.Larsson R. Zeolite catalysis and molecular vibrations. Catalysis Today. 1988;3:387–394. [Google Scholar]
- 42.Liu B, Hui K, Qin F. Thermodynamics of heat activation of single capsaicin ion channels VR1. Biophys. J. 2003;85:2988–3006. doi: 10.1016/S0006-3495(03)74719-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yao J, Liu B, Qin F. Rapid temperature jump by infrared diode laser irradiation for patch-clamp studies. Biophys. J. 2009;96:3611–3619. doi: 10.1016/j.bpj.2009.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Yao J, Liu B, Qin F. Kinetic and energetic analysis of thermally activated TRPV1 channels. Biophys. J. 2010;99:1743–1753. doi: 10.1016/j.bpj.2010.07.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Gupta S, Auerbach A. Temperature dependence of acetylcholine receptor channels activated by different agonists. Biophys. J. 2011;100:895–903. doi: 10.1016/j.bpj.2010.12.3727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gupta S, Auerbach A. Mapping heat exchange in an allosteric protein. Biophys. J. 2011;100:904–911. doi: 10.1016/j.bpj.2010.12.3739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Calderone CT, Williams DH. An enthalpic component in cooperativity: the relationship between enthalpy, entropy, and noncovalent structure in weak associations. J. Am. Chem. Soc. 2001;123:6262–6267. doi: 10.1021/ja003016y. [DOI] [PubMed] [Google Scholar]
- 48.Sharp K. Entropy-enthalpy compensation: fact or artifact? Protein Sci. 2001;10:661–667. doi: 10.1110/ps.37801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Prabhu NV, Sharp KA. Heat capacity in proteins. Annual Review of Physical Chemistry. 2005;56:521–548. doi: 10.1146/annurev.physchem.56.092503.141202. [DOI] [PubMed] [Google Scholar]
- 50.Cooper A. Thermodynamic analysis of biomolecular interactions. Curr. Opin. Chem. Biol. 1999;3:557–563. doi: 10.1016/s1367-5931(99)00008-3. [DOI] [PubMed] [Google Scholar]
- 51.Seldeen KL, McDonald CB, Deegan BJ, Bhat V, Farooq A. Dissecting the role of leucine zippers in the binding of bZIP domains of Jun transcription factor to DNA. Biochem. Biophys. Res. Commun. 2010;394:1030–1035. doi: 10.1016/j.bbrc.2010.03.116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kuroki R, Nitta K, Yutani K. Thermodynamic changes in the binding of Ca2+ to a mutant human lysozyme (D86/92). Enthalpy-entropy compensation observed upon Ca2+ binding to proteins. J. Biol. Chem. 1992;267:24297–24301. [PubMed] [Google Scholar]
- 53.Houk KN, Leach AG, Kim SP, Zhang XY. Binding affinities of host-guest, protein-ligand, and protein-transition-state complexes. Angewandte Chemie-International Edition. 2003;42:4872–4897. doi: 10.1002/anie.200200565. [DOI] [PubMed] [Google Scholar]
- 54.Starikov EB, Norden B. DNA duplex length and salt concentration dependence of enthalpy-entropy compensation parameters for DNA melting. J. Phys. Chem. B. 2009;113:11375–11377. doi: 10.1021/jp903924j. [DOI] [PubMed] [Google Scholar]
- 55.Liu G, Gu D, Liu H, Ding W, Luan H, Lou Y. Thermodynamic properties of micellization of Sulfobetaine-type Zwitterionic Gemini Surfactants in aqueous solutions--a free energy perturbation study. J. Colloid Interface Sci. 2012;375:148–153. doi: 10.1016/j.jcis.2012.02.027. [DOI] [PubMed] [Google Scholar]