Detectable signals of episodic risk effects on acute HIV transmission: Strategies for analyzing transmission systems using genetic data

Abstract

Episodic high-risk sexual behavior is common and can have a profound effect on HIV transmission. In a model of HIV transmission among men who have sex with men (MSM), changing the frequency, duration and contact rates of high-risk episodes can take endemic prevalence from zero to 50% and more than double transmissions during acute HIV infection (AHI). Undirected test and treat could be inefficient in the presence of strong episodic risk effects. Partner services approaches that use a variety of control options will be likely to have better effects under these conditions, but the question remains: What data will reveal if a population is experiencing episodic risk effects? HIV sequence data from Montreal reveals genetic clusters whose size distribution stabilizes over time and reflects the size distribution of acute infection outbreaks (AIOs). Surveillance provides complementary behavioral data. In order to use both types of data efficiently, it is essential to examine aspects of models that affect both the episodic risk effects and the shape of transmission trees. As a demonstration, we use a deterministic compartmental model of episodic risk to explore the determinants of the fraction of transmissions during acute HIV infection (AHI) at the endemic equilibrium. We use a corresponding individual-based model to observe AIO size distributions and patterns of transmission within AIO. Episodic risk parameters determining whether AHI transmission trees had longer chains, more clustered transmissions from single individuals, or different mixes of these were explored. Encouragingly for parameter estimation, AIO size distributions reflected the frequency of transmissions from acute infection across divergent parameter sets. Our results show that episodic risk dynamics influence both the size and duration of acute infection outbreaks, thus providing a possible link between genetic cluster size distributions and episodic risk dynamics.

Introduction

HIV incidence in the United States continues to rise among men who have sex with men (MSM) (Hall et al., 2008; Prejean et al., 2011). Several control strategies such as Test & Treat have been devised and implemented in order to stop HIV transmission among MSM. Pre-exposure prophylaxis (PrEP) has recently gained prominence as several studies show the efficacy of this type of intervention in controlling HIV spread (Wainberg, 2011). Nevertheless, effective application of intervention policies requires an understanding of key determinants that affect the transmission dynamics of the HIV epidemic in a MSM population. The goal is therefore to determine what we need to understand about the MSM HIV transmission system to guide PrEP-based decisions.

A key objective for effectively guiding PrEP-based interventions is to understand the role of transmissions during acute infection (hereafter, “acute transmissions”) in sustaining the chains of HIV transmissions at the endemic level (Jacquez et al., 1994; Koopman et al., 1997). Simulation-based studies focusing on various aspects of HIV transmission dynamics among MSM include examinations of episodic risk behavior (Koopman et al., 2005; Zhang et al., 2012), heterogeneous contact rates (Romero-Severson et al., 2012), insertive and receptive behavior (Alam et al., 2010; Goodreau and Golden, 2007), and partnership duration and concurrency (Kim et al., 2010; Powers et al., 2011; Volz et al., 2010). These studies show that such behavioral aspects, under various configurations, can indeed increase the proportion of acute infection transmissions at endemic equilibrium. We are therefore interested in understanding to what extent and in what ways acute transmissions contribute to endemic HIV transmission dynamics.

We believe that estimating the fraction of transmissions occurring during acute HIV infection is a key to successful application of the PrEP intervention strategy. The most valuable aspect of genetic surveillance analyzed with transmission models, as compared to traditional surveillance is that it can reveal patterns of transmissions by stage of infection. It may also help in estimating the probability that a particular transmission will lead to a chain of further transmissions or lead to a dead-end. The distribution of infection cluster sizes at different genetic distances provides powerful information on the fraction of transmissions from the acute infection stage.

From a modeling perspective, incorporating realistic but previously ignored aspects of MSM transmission and their effect on acute transmission clusters could help in guiding interventions such as PrEP. The size distribution of acute transmission clusters could have a strong impact on what intervention strategies might work best. For example, focusing partner services on contacts that are likely to be part of sizeable acute infection clusters may help reduce the total number of individuals who must be reached for PrEP in order to produce a given reduction in the incidence rate. Several studies have reported phylogenetic clustering of sequences from which the contribution of the acute infection period in sustaining transmission in a population may be estimated (see Brenner et al., 2011). This may help to diagnose cases earlier and may increase the efficacy of PrEP, with or without the Test & Treat strategy. A pertinent question then is whether the acute transmissions whose numbers we can estimate make up many small outbreaks that are sporadic, with no special role in sustaining the chains of transmission, or whether they make up larger outbreaks that are key elements in sustaining transmission chains. In other words, are acute transmission chains long enough for interventions targeting acute infection outbreaks (AIOs) to have big practical effects? Our objective is to look for transmission model characteristics that could have an effect on cluster size distributions, the distribution of lengths of chains of acute transmission, and the fraction of transmissions from acute infection. In this paper, we present our conceptualization of the acute infection outbreaks and a strategy to infer acute clustering patterns from the available genetic data. We then explore a model of episodic risk to demonstrate methods based on individual-based simulations to record and analyze acute outbreaks.

Conceptualizing acute HIV outbreaks

The properties of acute infection outbreaks (AIOs) could differ between transmission systems in ways that may affect which PrEP strategy is most effective even when those systems have the same joint distribution of the number of times an individual transmits during acute infection and the number of times he transmits during chronic infection. Here, by acute infection outbreaks, we mean clusters of acute transmissions that are separated from other acute infection outbreaks by chronic stage transmissions in a transmission tree. Notice that the operational definition of an ‘acute’ stage may depend upon the research setting; for example, Brenner et al. (2011) uses a six-month threshold for acute HIV clusters.

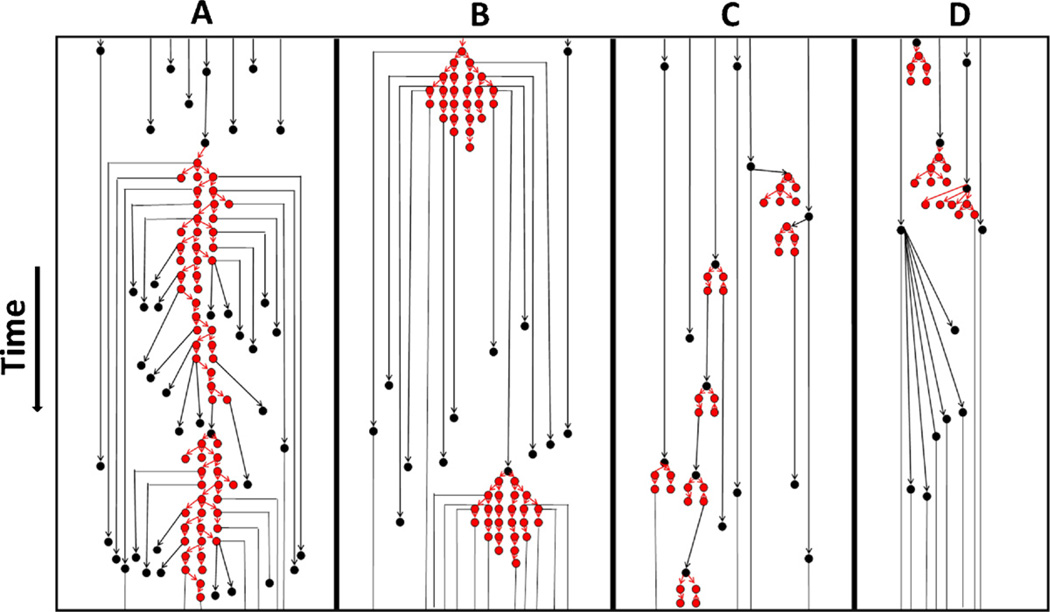
The four hypothetical systems (A–D) depicted in Fig. 1 illustrate what we might expect in terms of the size and shape of acute infection outbreaks under different transmission systems. As shown in the figure, different patterns reflect different roles of acute HIV infection (AHI) in sustaining transmission given the same fraction of transmissions from AHI. The red nodes in Fig. 1 represent individuals who were members of an acute infection outbreak, i.e., those who were infected by an acute stage infector. The black nodes in the figure represent individuals who were infected by an infector in chronic stage and were therefore not members of an acute infection outbreak. The red and black arrows depict that the transmission event occurred when the infector was in acute and chronic stages respectively. The length of the arrows represents the time since the infector’s own infection: red arrows are drawn as shorter than black arrows because acute transmissions happen sooner after the infector was infected than chronic transmissions. Notice that the four systems in Fig. 1 only communicate the concept of acute infection outbreaks and that they may vary in size and shape under different settings.

Fig. 1.

An illustration of four different hypothetical transmission systems (A–D) showing acute infection outbreaks of different sizes and shapes. Black circles: someone infected from a chronic infection source; red circles: someone infected from an acute infection source. Black arrows: transmissions during chronic stage; red arrows: transmissions during acute stage. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

The first transmission system ‘A’ shown in Fig. 1 gives an example of two acute infection outbreak clusters with long chains but only a modest degree of branching, separated by a single chronic transmission. Notice that in this system, infection was sustained mostly by acute stage transmissions in the form of these outbreak clusters. In system ‘B’, there are once again two large acute outbreak clusters linked by a single chronic transmission, but with a shorter duration and more branching. In system ‘C’, acute transmissions occur in small sized clusters and together with chronic transmissions contribute to sustaining transmissions. Lastly, in system ‘D’, we find acute transmissions clustered in small sized outbreaks but all except one lead to dead-end transmissions.

In our individual-based simulations, we generate a forest of transmission trees instead of a single rooted tree. The hypothetical transmission systems presented in Fig. 1 illustrate our notion of transmission forests and acute infection outbreak clusters. A set of randomly selected individuals (default: 1%) in the populations is seeded with HIV infection at the start. Each of these initially infected individuals become roots of transmission trees and in turn, become potential initiators of transmission chains. We then track the transmission chains that survive until the endemic period and those that lead to a dead-end. We consider a transmission tree as a directed ‘genealogical’ tree of infections, where individuals are nodes connected by arcs (or directed edges), representing transmission events (cf. Welch, 2011). Acute infection outbreaks are thus subtrees that are extracted by removing chronic transmissions (edges) from a transmission tree.

In our context, a new acute infection outbreak starts when an individual infected by a chronic stage infector transmits infection to a susceptible while still in his own acute stage. This is depicted in Fig. 1 as a black node (an individual infected by a chronic stage transmission) being a parent of a red node (an individual infected by an acute stage transmission) by a red arrow (acute stage transmission). A subsequent acute stage transmission from an individual who is part of an acute infection outbreak includes the newly infected individual in that outbreak. An outbreak’s size increases when there is a secondary acute infection transmissions resulting from its members. Once an individual is included in an acute infection outbreak (AIO), he remains a part of that outbreak forever, and so the size of an AIO is strictly non-decreasing. The final size of an acute infection outbreak is defined as the total number of transmissions during the time it was active. The minimum size of an outbreak is 1 (i.e., a single acute transmission from an individual infected by a chronic stage infector to an individual who only subsequently transmits while in chronic stage or not at all) and is referred to as an ‘isolate’.

We define the duration of an outbreak as the time between the last and the first transmission. The branch length of an edge is the time since the infection of the parent node. The height of an outbreak (subtree) is the longest path from a root of an outbreak to its leaf node. An acute infection outbreak ends when all of its members have either progressed to the secondary infection stage or became sexually inactive (i.e., exit from the system). An internal node in an outbreak is an individual who transmitted at least once while still in the acute stage of infection. A leaf node in an outbreak is an individual that did not transmit during his acute stage. If an individual generated no secondary infections (acute or chronic) during its lifetime, the corresponding node is a dead-end.

Strategy for inferring acute clustering patterns and PrEP effects

The fraction of transmissions from the acute stage of infection may be determined by the relative biological potential for transmission, contact patterns, and other behavioral patterns. The estimated contribution of acute transmissions varies widely (cf. Pilcher et al., 2007) and the only good available estimates come from the Rakai Study in Uganda by Wawer et al. (2005) for heterosexual couples.

Currently we cannot detect acute HIV infection (AHI) outbreak patterns directly. Although methods for investigating the outbreak patterns, such as contact tracing, worked for gonorrhea (Blount, 1972; Potterat and Rothenberg, 1977), they still have limited ability to infer the fraction of HIV transmissions by stage of infection. In this respect, phylogenetic studies are likely to be more effective at inferring that fraction by examining genetic clusters and how they may reflect the extent of transmission from AHI.

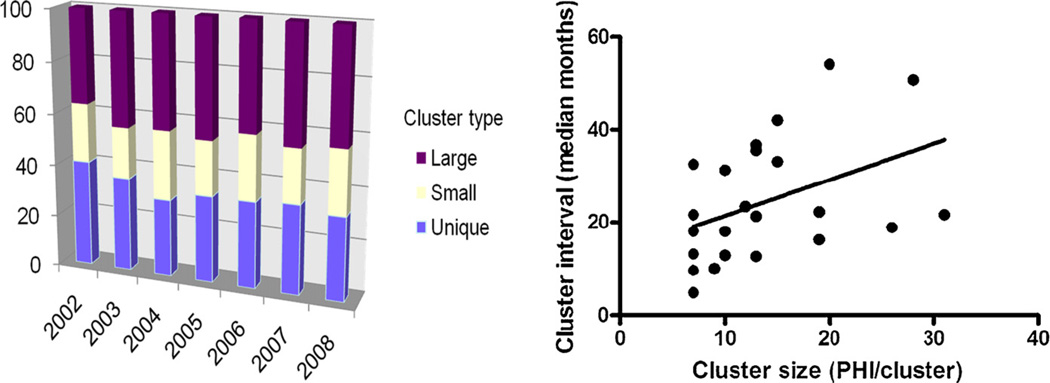
Marked genetic clustering patterns were observed in Montreal that were thought to indicate a high fraction of acute infections (Brenner et al., 2011; Brenner and Moodie, 2012). In Fig. 2, the left panel shows the phylogenetic relationship among collected sequences in a recent study from Brenner and Moodie (2012). The Montreal analysis used a narrow definition of clusters (1% distance, >99% support) (Fig. 2). New clusters of all sizes are continually forming and dying out in a manner that brings cluster size distributions more or less into equilibrium (Fig. 2; left panel). Recent advances, in particular the methods developed by Volz et al. (2009, 2012), are promising as a way of estimating this contribution from the shape of phylogenetic trees, under the assumptions that such phylogenetic trees reflect actual transmission trees. Other studies, such as Leigh Brown et al., 2011) have used genetic clustering to infer contact patterns.

Fig. 2.

Phylogenetic cluster analysis from Montreal (source: Brenner and Moodie, 2012). Left: New primary HIV (PHI) clusters forming and dying out in a manner that brings the conformation of clustering patterns to equilibrium. Right: Interrelation of the size of 23 large PHI clusters and their median duration (in months).

There are several reasons for acute infection sequences to cluster more than chronic sequences. First, chronic sequences have diverged from the viruses with which they are infected more than the acute stage infections. Second, an individual infected from an acute source case is more likely to transmit during acute infection, possibly because they are more likely to be part of a high-contact group (Koopman et al., 1997). Moreover, such differences will be greater when the acute infection-sampling fraction gets higher.

In addition to the fraction of transmissions from acute infection, several other important quantities may also be inferred by acute transmission cluster analysis. For example, one could calculate the fractions of acute and chronic transmissions that are dead-end, single, or multiple. This is important, because it allows us to calculate how many downstream infections we would expect to prevent by preventing a transmission during acute versus chronic infection, which is important to know in order to allocate limited resources efficiently. We can also calculate the distribution of lengths of acute transmission chains, in order to determine whether partner services is likely to be able to determine that an acute infection outbreak is occurring early enough in that outbreak to prevent key sustaining transmissions. The composition of AHI clusters can also be informative as to whether the AHI outbreaks largely occur within mixing groups, or whether acute transmissions provide higher chances of dissemination between mixing groups than chronic transmissions.

Besides genetic studies, multiple sources of information and data would help better guide PrEP decisions, but there remain uncertainties and limitations about the capacity of currently available sources in achieving such objectives. Surveillance and partner services data cannot do this job directly. Studies of transmission risks by stage such as Wawer et al. (2005) would be informative for PrEP decisions but are likely to be too expensive and difficult for routine use. Additionally, most current behavioral surveys do not address contact rate volatility or mixing group issues, which would be important factors to consider in order to better guide the allocation of PrEP. Fitting transmission models to surveillance data could help estimate transmission parameters. However, HIV transmission systems are complex, and we need a way of providing face validity for parameter estimates and a way of determining what simplifying model assumptions should be relaxed to insure that inferences about the fraction of transmissions from AHI are robust to realistic relaxation of these simplifying assumptions. When incorporating realistic aspects into the model, one should avoid model misspecification. Model misspecification may result in poor parameter identifiability, which occurs when there is not a unique correspondence between the input variables and output variables, so that the model is less useful for inferring a particular parameter from observed data (Jacquez, 1985).

Related work on measuring transmission- and phylogenetic clusters

A number of recent papers have addressed the issue of analyzing distributions of various measures of transmission trees and genetic clusters using phylodynamic analysis and/or transmission models (see Danon et al., 2011; Graw et al., 2012). In an older but still relevant paper, Murray (2002) used a microsimulation model to generate dynamic transmission chains of tuberculosis and examined the epidemiological and demographic determinants of the mean size of clusters and the proportion of isolates. Rocha et al. (2011) looked at the distribution of average outbreak sizes generated from specific contact network topologies. Grassly and Fraser (2008) reported offspring and generation-time distribution of a transmission tree for models of influenza, malaria and HIV. Leventhal et al. (2012) studied how measures of transmission tree imbalance may change under different configurations of the underlying contact structures. Wagner et al. (2012) investigated cluster size distributions and temporal dynamics of HIV strains. A phylodynamic analysis of a sample of HIV-positive MSM in the United Kingdom by Leigh Brown et al. (2011) showed a skewed distribution of cluster sizes, which could be approximated by a power law distribution or another fat-tail distribution. Their results may be compared with the distributions of primary HIV clusters that are reported by Brenner and Moodie (2012), which shows a high proportion of isolates and clusters of sizes of at most 2, and a skewed distribution of large clusters. Elsewhere, Lewis et al. (2008) showed how the observed size distribution of genetic clusters indicates a higher contribution of acute stage infection in sustaining HIV transmission in the studied population. O’Dea and Wilke (2011) reported strong effects of contact heterogeneity on the various measures of structures of genealogies. Prosperi et al. (2011) performed a topological analysis of a maximum-likelihood phylogenetic tree by examining the distribution of median branch length and the number of nodes against levels of the tree. They also reported histograms of cluster size distributions of the sequences and investigated how the maximum cluster size related to the number of isolates. Welch (2011) studied the link between various contact networks and properties of their simulated transmission trees by applying summary measures such as the mean internal and external branch lengths, distribution of number of secondary infections by an infected individual, and the number of “cherries” (pairs of leafs that are more closely related to each other than either is to any other leaf) in a tree as a fraction of the maximum possible number of cherries for a tree of that size.

Building upon a growing body of literature, we are interested in what aspects of reality (such as episodic risk) affect the dynamics of acute infection outbreaks and the properties of transmission trees. We seek to explore what information on these key parameters and/or their interaction might potentially be found in genetic sequence data. As a first step toward this analysis, we applied several measures of transmission trees and phylogenetic clusters, some of which are reported in the above-mentioned studies for this purpose, to the results of individual-based simulation models. Recent work by Welch (2011) involves the application of size and shape measures to simulated transmission trees, although the kind of contact pattern clustering investigated by Welch does not relate directly to the clustering of acute transmission that we are interested in this paper.

Materials and methods

In this section, we first give an outline of an episodic risk model that is used, as a demonstration, to examine model features that affect both the episodic risk effects and the shape of transmission trees. The effect of the model parameters on population-level outcomes such as endemic prevalence and the fraction of transmissions from acute infections are reported from Zhang et al. (2012), using a deterministic compartmental model (Anderson and May, 1991). We used that model’s stochastic, individual-based counterpart to generate simulated transmission trees. We then extracted from those transmission trees the acute infection outbreaks (clusters), i.e., those outbreaks that are formed out of transmissions from individuals in their acute HIV stage. A list of model parameters, an outline of the individual-based model and a set of differential equations for the deterministic compartmental model are given in Appendix ‘A’. Lastly, we present a scheme to record such outbreaks during a simulation run and a summary of outcome measures.

An episodic risk model with infection stages

Our episodic risk model consists of two risk phases (high and low) that are defined by their respective (high and low) contact rates. These are determined by the average contact rate in the entire population (which is fixed) and the ratio of high-to-low contact rates, which is a key parameter. We assume instantaneous sex acts and no long-term sexual partnerships. The natural history of HIV is modeled as two stages of infection, i.e., an acute HIV stage of high infectivity and a chronic HIV stage of low infectivity. There are two sexual mixing sites: an exclusive high-risk mixing site, where only the high-risk individuals make sexual contacts and a general (common) mixing site, where both high- and low-risk individuals mix, proportional to their respective contact rates. The model parameter π determines the fraction of contacts by high-risk individuals that are made at the high-risk mixing site. We assume a constant birth and death rate in the model. The baseline transmission probability per sex act is adapted from Vittinghoff et al. (1999). The average duration of the acute stage of infection is assumed to be 2 months whereas the average duration of chronic stage is assumed to be 10 years (cf. Pilcher et al., 2007).

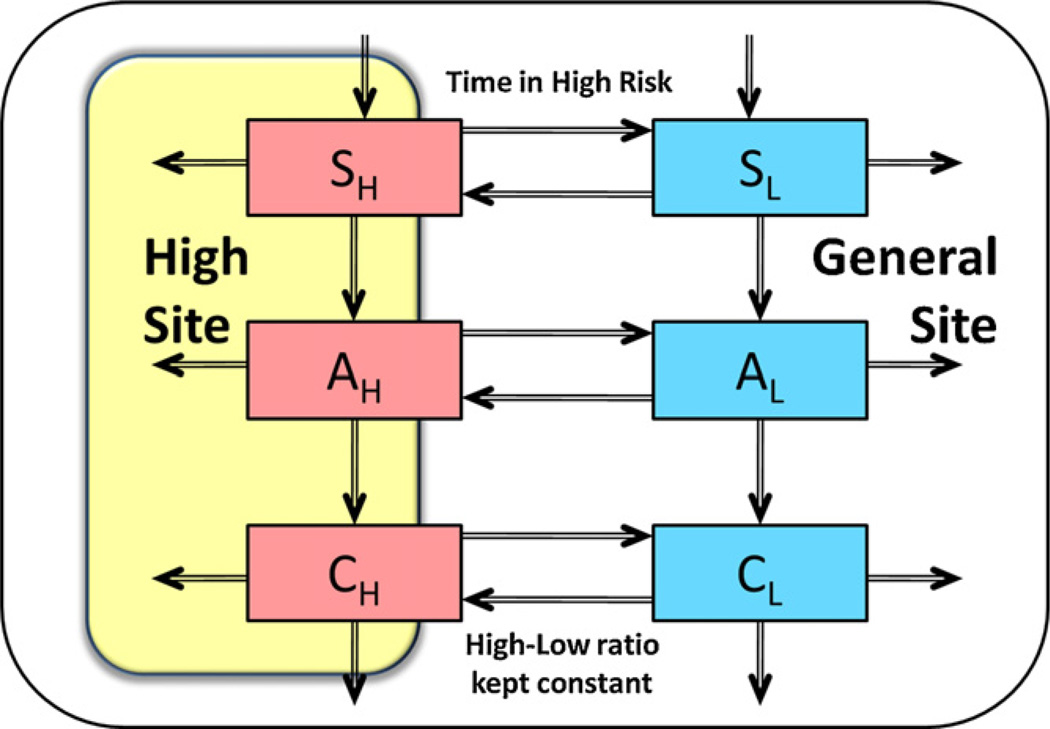
Fig. 3 shows a schematic diagram of the episodic risk model. The compartments S*, A* and C* in the conceptual diagram refer to sub-populations that are susceptible, acutely infected, and chronically infected, respectively. The subscripts H and L refer to the subpopulations that are in the high-risk and low-risk phases, respectively. Episodic risk is a product of the turnover between the two risk phases. This turnover is determined by the average duration of a stay in the high-risk phase and by the average fraction of the population that is in the high-risk phase at any given time, in the absence of HIV. A faster turnover rate means that the individuals spend shorter time in the high-risk phase, and thus implies more volatile sexual risk behavior. Further description of the deterministic model and the references for the epidemiologically related parameters are presented in Zhang et al. (2012).

Fig. 3.

A schematic diagram of the episodic risk model showing the two sexual mixing sites (high-risk and general), wherein the subscripts denote the two risk phases (high ‘H’ and low ‘L’) and the two stages of HIV infection (acute ‘A’ and chronic ‘C’).

Recording acute infection outbreaks using individual-based models

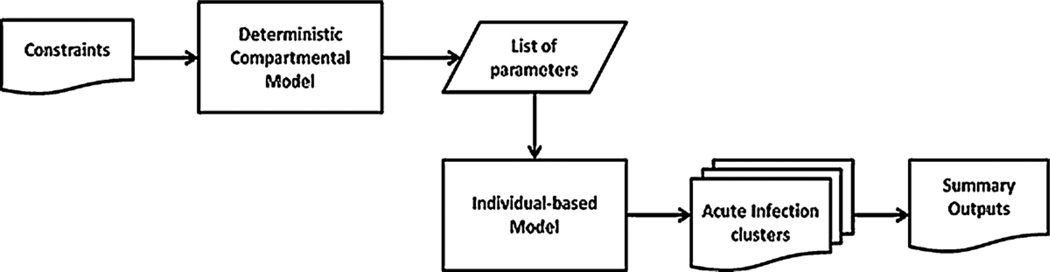
Our method to generate and record acute infection outbreaks (AIO) works as follows: we use a deterministic compartmental model to generate a list of parameters that generates results that match a set of given constraints (e.g., constraining on endemic prevalence). We then use that model’s stochastic, individual-based counterpart that takes the same parameters as an input and generates acute infection outbreaks. These simulations generate output variables at the population level as well as those output variables concerned with the acute outbreak clusters. Fig. 4 gives an overview of the methodology we have used to generate these results.

Fig. 4.

A schematic diagram showing the process of generating acute infection outbreaks statistics using the deterministic compartmental and its stochastic individual-based counterpart.

In order to record AIOs, we have developed a scheme that is independent of a transmission model and can easily be integrated with any individual-based model (IBM) of HIV spread. Table 1 presents the steps involved in recording the acute infection outbreaks in a simulation run. Further details on the individual-based model version and a technical description of our acute infection outbreaks library (in Java) are given in Appendix ‘B’. In this appendix, we also demonstrate the integration of our current AIO recorder with two different individual-based models.

Table 1.

Steps in recording early infection outbreaks in a simulation run.

Let the simulation run until the system is at endemic equilibrium. At time t1 at endemic equilibrium, start recording new acute infection outbreaks, treating all infected individuals in the early stage as potential initiators of an outbreak. Record new acute infection outbreaks for the next 30 years. Stop simulation when all the acute infection outbreaks that were recorded during that 30-year period have ended. Ignore outbreaks that begin more than 30 years after t1.

Note that in this paper, we report simulation results for acute infection outbreaks that are recorded at endemic equilibrium. As discussed earlier, results from the Montreal study by Brenner et al. (2011) seem to suggest that the distribution of sizes of acute infection outbreaks is at equilibrium. A detailed analysis and comparison of outbreaks that are generated during the initial and endemic periods will be presented separately.

Output measures used for analysis

Population-level outputs

For each parameter set used in the simulation experiments, we record endemic prevalence of HIV infection in the simulated population. The endemic prevalence of infection in the high-risk and low-risk populations is recorded separately. Another important output variable is the fraction of transmissions from acute and chronic HIV infections, which is measured by the proportion of new infections from the acute stage that are recorded during the observed period.

Measuring size and shape distributions of acute infection outbreaks

We examine several aspects of acute infection outbreaks, based on the outputs generated in a simulation run. We present a summary of outputs for each parameter set, averaging over 10 simulation runs, to show how the size and shape of acute outbreak distributions may change with respect to different parameter sets.

The AHI outbreak measures explored in this paper allow us to observe only some of the different aspects of transmission clusters illustrated in the conceptual framework shown in Fig. 1. Our aim is to incorporate the existing measures for cluster sizes and shapes of transmission trees (see Section “Related work on measuring transmission- and phylogenetic clusters”) in the Java library we are currently developing for use with any individual-based HIV transmission model. The technical description provided in Appendix ‘B’ outlines those measures that are already implemented. Using our library, one can output statistics that apply to both generational infection trees and the corresponding lineage-based transmission trees (Welch et al., 2011). Using our library, one could also transform a generational transmission tree into a lineage-based transmission tree (cf. Grassly and Fraser, 2008) to measure tree imbalance and other tree shape statistics (cf. Leventhal et al., 2012; Rocha et al., 2011; Welch, 2011) under different transmission model conformations. However, this type of analysis will be presented separately.

Results

How the timing of high contact rate behaviors affects transmission dynamics at the population-level

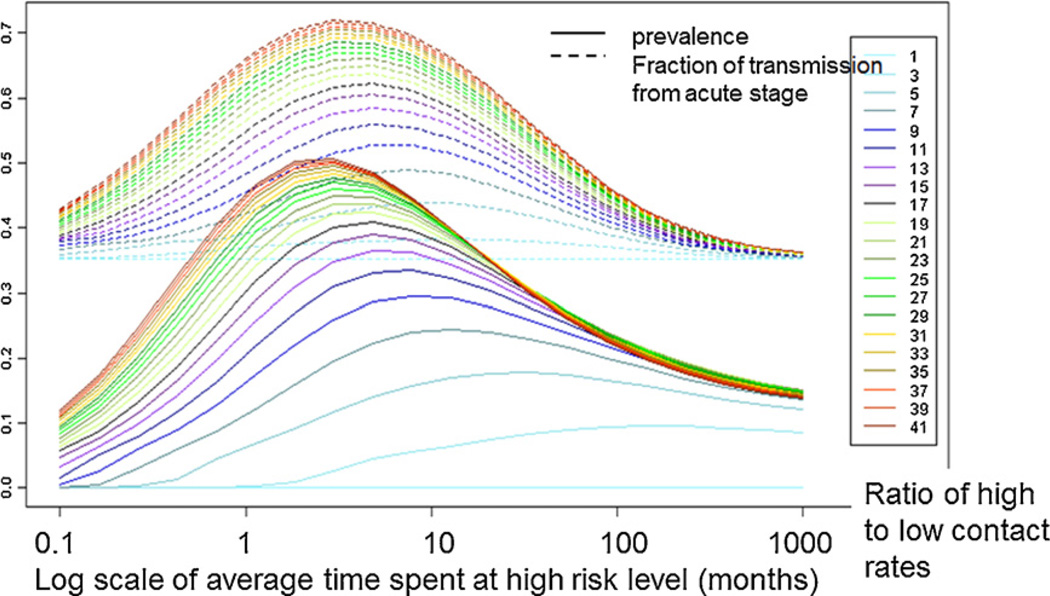
One of the aspects of the deterministic episodic risk model explored by Zhang et al. (2012) was the effect of average duration of stay in the high-risk (high contact rate) phase. This model parameter determined the turnover rate of individuals from the high-risk group to the low-risk group, and vice versa. Keeping the average contact rate in the population unchanged, how often individuals fluctuate between high and low contact rates markedly affects HIV prevalence and the fraction of transmissions that arise during acute infection at endemic stage as shown in Fig. 5. Here, two model parameters: the ‘duration of stay in high-risk phase’ (from 0.1 to 1000 months), and the ‘ratio of high-to-low contact rates’ (from 1 to 41) were explored. The ‘transmission potential’ parameter in Fig. 5 is kept fixed at 0.35. Zhang et al. define ‘transmission potential from AHI’ to be the fraction of transmissions that occurs during acute infection stage (AHI) under a homogeneous contact-rate scenario. That is, when the contact rates are equal, the fraction of acute transmissions equals the fraction of transmission potential from AHI. This effect is reflected by the lowest flat dashed line in Fig. 5, which corresponds to the value 0.35 on the left Y-axis. A detailed analysis of the effect of episodic risk model parameters is presented in Zhang et al. (2012).

Fig. 5.

Prevalence and fraction of transmissions from acute stage from the deterministic episodic risk model versus the duration of stay in the high-risk phase (0.1–1000 months in log-scale) and the ratio of high-to-low contact rates (1–41). The transmission potential from acute infection stage was kept fixed at 0.35.

As Fig. 5 shows, the effect the ‘ratio of high-to-low contact rates’ on the fraction of acute transmissions is monotonic across different values of the duration of stay in high-risk phase. When increasing from low to intermediate values, this ratio also leads to an increased endemic prevalence across different values of the ‘duration of stay in high-risk’ parameter, but as this ratio further increases from an intermediate value, the endemic prevalence decreases when the duration of stay at high-risk is longer than 20 months. To understand this pattern, it is necessary to understand the underlying dynamics. With or without episodic risk, susceptibles in the high-risk group will be infected at a higher rate than susceptibles in the low-risk group due to their higher contact rate. In the complete absence of episodic risk, (the limit as duration of stay in high-risk phase becomes infinite), individuals infected in one phase will spend the entire duration of their infection in that phase, and so the fraction of acute transmissions will be equal to the transmission potential. In the opposite limit, where duration of stay in high-risk phase = 0, the risk groups are meaningless since switching between the two risk phases happens at an infinitely high rate (not shown in Fig. 5). Hence, the system is effectively homogeneous and the fraction of acute transmissions again equals the transmission potential. In between these two extremes, however, the dynamic is much different: on average, a newly infected individual will spend a greater fraction of his acute infection than of his chronic infection in the risk phase in which he was infected. Therefore, individuals infected while in a high-risk phase will generate a fraction of acute transmissions that is greater than the transmission potential, while individuals infected while in a low-risk phase will generate a fraction of acute transmissions that is less than the transmission potential. Therefore, the greater the difference between the rates at which high-risk susceptibles and low-risk susceptibles are infected (due to a greater ratio of contact rates) is, the greater the fraction of transmissions that come from acute infection will be.

With the exception of the homogeneous contact rate scenario, individuals who have recently had a large number of sexual contacts have a higher average contact rate than individuals who have had fewer recent sexual contacts. This is the basic cause for the elevation of the fraction of acute transmissions above the acute transmission potential. This effect is a product of common causation (individuals who have recently been in a high-risk phase are more likely to have recently had a large number of sexual contacts, and are also more likely to still be in a high-risk phase, which increases their average contact rate).

The situation is more complex when it comes to prevalence. Newly infected high-risk individuals are more likely to spend their highly infectious acute period in the high-risk phase, which, in this symmetrical model, equates to a higher risk of transmitting as well as a higher risk of being infected. Thus, the same increase in high-risk incidence at the cost of low-risk incidence due to an increase in the high-to-low contact rate ratio that drives an increase in the fraction of acute transmissions, also results in an increase in prevalence, to a point. However, as the contact rate ratio increases at a fixed average contact rate and duration of stay in high-risk phase, the high-risk phase becomes increasingly saturated with infection. Consequently, past a certain point, the negligible increase in high-risk incidence with an increasing contact rate ratio is more than counterbalanced by the decrease in low-risk incidence. Because higher levels of episodic risk behavior (lower values of the duration of stay in the high-risk phase) result in more rapid replenishment of susceptible individuals in the high-risk phase, this effect is seen at a lower contact rate ratio for longer durations of stay in the high-risk phase.

At high contact-rate ratios, the fraction of transmissions that are from low-risk individuals is greatly reduced, but not to such an extent as to be barely happening. This can be seen in Zhang et al. (2012; Fig. 5B and D). As shown in Zhang et al. (2012), although we observe significant transmissions from the low-risk population even under high values of the contact rate ratio, and the replenishment of infected individuals in the low-risk phase due to episodic risk can in some cases result in the number of such transmissions being higher than in the homogeneous case, for all parameter values explored, the fraction of all transmissions that are from low-risk infectors is lower than in the homogeneous case (Zhang et al., 2012; Fig. 5B and D).

How the timing of high contact rate behavior affects acute infection outbreaks

While the deterministic compartmental episodic risk model gives insight on how different aspects of the model affect the population level prevalence and fraction of acute transmissions, we developed its stochastic individual-based (IBM) counterpart to understand those aspects’ effect on the characteristics of acute infection outbreaks. For the individual-based simulations, we constrained the endemic prevalence to be 0.45 across all parameter settings so that, on average, the total number of transmissions remained the same while the fraction of transmissions from acute stage varied under different parameter settings. This was done using Python’s SciPy^® library to solve the deterministic compartmental version of the episodic risk model. Table 2 presents the episodic risk model parameters and their corresponding ranges that were explored in our simulation experiments.

Table 2.

Model parameters and the ranges explored, constraining endemic prevalence to be 0.45.

Parameter	Range explored
Acute transmission potential (X)	{0.1, 0.3, 0.5, 0.7}
Average duration of a stay in the   high-risk phase in months (durH)	{[2–10], [20–30], [30–40], [50–60], [80–90]} step-size: 2
High-to-low contact rate ratio (rCHL)	{1, 10, 20, 30}
Fraction of the population that is in the   high-risk phase at infection-free   equilibrium (FrH)	{0.1, 0.2, 0.3}
Fraction of high-risk contacts made at   the high-risk mixing site (FHatH)	{0.1, 0.5, 0.9}

Results based on specific parameter sets

The results reported in Section “How the timing of high contact rate behaviors affects transmission dynamics at the population-level” highlight the three model parameters having substantial effects on the fraction of transmissions from AHI. These are the ‘high-to-low contact rate ratio’ (rCHL), the ‘duration of stay in high-risk phase’ (durH), and the AHI ‘transmission potential’ (X). We start with specific parameter sets consisting of low and high values for the transmission potential (0.1 and 0.5) and the high-to-low contact ratio (1 and 30). We show results for five values of the duration of stay in high-risk behavior parameter (2, 10, 30, 60 and 90 months). We fixed the values of the remaining two parameters FrH and FHatH at 0.1 and 0.9 respectively.

The transmission potential from acute infection is the expected fraction of transmissions from acute infection in a completely homogeneous population that mixes homogeneously. Under a homogeneous contact rate, i.e., when rCHL is 1, the fraction of transmissions from AHI is on average equal to the corresponding AHI transmission potential (X). On the other hand, when the value of rCHL is 30, the average contact rate of the high-risk population is 30 times higher than the low-risk population. Here, the fraction of transmissions from AHI is expected to rise above the transmission potential.

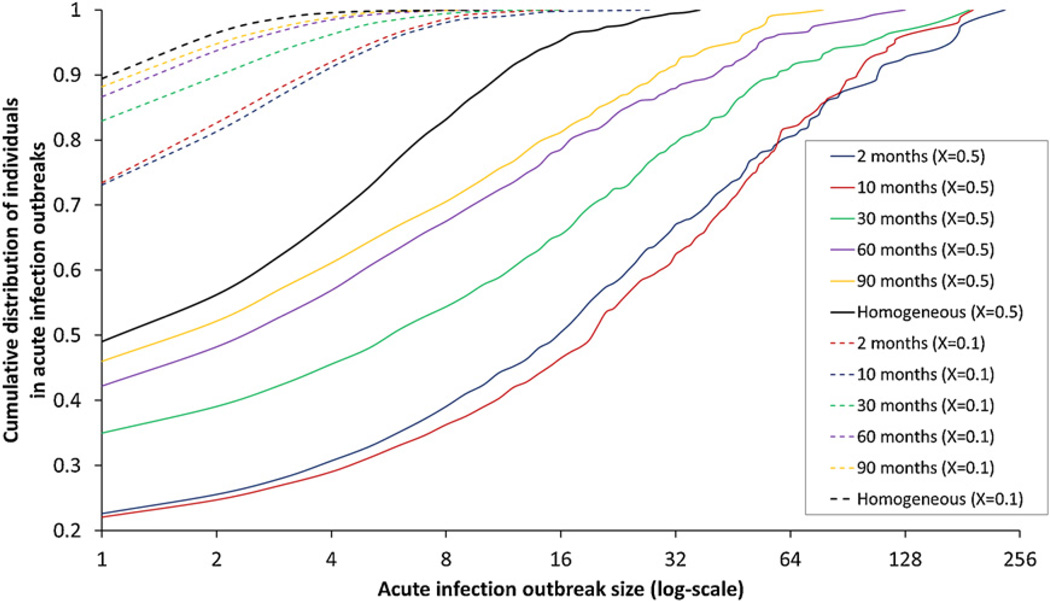
In order to understand the effect of the above-mentioned parameters on the clustering of acute transmissions, we first look into the cumulative size distribution of acute infection outbreaks (AIO) shown in Fig. 6. These plots give the total fraction of clustered acute transmissions that are in AIO of a certain size or smaller. The plots are grouped with respect to the corresponding value of the transmission potential (X), with the solid and dashed lines referring to X = 0.5 and X = 0.1 respectively.

Fig. 6.

Cumulative size distribution plots of acute infection outbreaks for the five duration of stay in high-risk phase values (2, 10, 30, 60, 90 months) and the two values of the high-to-low contact ratio (rCHL); colored lines (rCHL = 30) and black lines (rCHL = 1). Solid and dashed lines correspond to the low (0.1) and high (0.5) values of the AHI transmission potential respectively.

In Fig. 6, the first point on the X-axis (plotted on a binary log scale) gives the fraction of transmissions from chronic stage for the respective parameter sets plus the fraction of individuals in AIO of size 1 (isolates). The next point gives the cumulative fraction of individuals that are in AIO of size less than or equal to 2, and so on. Colored lines in the figure refer to the five values of the durH parameter for a high contact rate ratio (rCHL = 30), whereas the black lines refer to homogeneous contact rate, i.e., for rCHL = 1. Under a homogeneous contact rate, we find similar outbreak size distributions regardless of the value of durH – indeed, in the corresponding deterministic model, they would be identical – and so a single plot is shown in the figure with the size distribution mediated by the given value of the AHI transmission potential.

As Fig. 6 shows, the outbreak size distribution is mainly driven by the fraction of transmission from acute infection, which, in addition to the transmission potential, is further affected by the duration of stay in high-risk and the contact rate ratio. For X= 0.5 (solid lines), we find large size outbreaks with a right-skewed distribution observed under a fast risk turnover (durH = 2) and a high value of the contact rate ratio (rCHL = 30). When the fraction of transmissions from AHI is high, the size distribution of AHI outbreaks can be fitted with a heavy-tailed distribution such as the Zipf distribution (Baek et al., 2011). This analysis will be reported separately. Nevertheless, it worth examining briefly why this is so.

A common model for a wide variety of processes is the Yule process (Simon, 1955), sometimes referred to as preferential attachment. In this model, there are a number of groups of objects, such as genera of species, frequency of words in text, or cities made up of people, to name just a few possibilities (Simon, 1955), and, at any given time, the probability of adding a new object to a particular group is proportional to the number of objects already in that group. When a Yule process is followed exactly, the distribution of final sizes of groups is expected to follow a heavy-tailed distribution known as the Yule or the Yule-Simon distribution (Simon, 1955). In our model, acute infection clusters are generated by a process very similar to a Yule process – at any given time, each acutely-infected individual in a particular outbreak has the potential to transmit infection to a susceptible, and thereby add that susceptible to that outbreak, and this potential is independent of the number of other acutely-infected individuals currently in that outbreak. The similarity is not an identity, both because of the role of progression to chronic infection and/or death in removing individuals from an outbreak, and because high-risk and low-risk susceptibles do not transmit at the same rate. Nevertheless, the similarities are great enough that we would expect the distribution of outbreak sizes to follow a heavy-tailed distribution, and this is indeed the case.

It is important to note here that this preferential attachment applies only to outbreaks, not to individuals. It is true that, with the exception of the homogeneous mixing scenario (rCHL = 1), individuals who have recently had a large number of sexual contacts have a higher average contact rate than individuals who have had fewer sexual contacts. However, this is a product, not of preferential attachment, but of common causation: Individuals who have recently been in a high-risk phase are more likely to have recently had a large number of sexual contacts, and are also more likely to still be in a high-risk phase, which increases their average contact rate.

Here, both parameters contribute to raising the fraction of transmission from AHI above the transmission potential, resulting in large outbreaks that are responsible for sustaining the transmission chains. With a slower risk turnover (i.e., larger values of durH), the fraction of AHI transmissions becomes closer to the transmission potential (X = 0.5 or 0.1, indicated by solid or dashed lines respectively). However, the combined effect of high contact rate ratio and risk turnover still generates outbreaks that are larger than those observed for the homogeneous mixing case (rCHL = 1). Notice that under the homogeneous mixing, we find 90% of the outbreaks having a size that is less than or equal to 10, indicating small and sporadic clusters of acute transmissions. This suggests that a heterogeneous contact rate in a population can generate larger outbreaks than we would observe under homogeneous mixing, even when risk turnover is slow, as seen by the substantial difference between the black and yellow solid curves.

The AHI clusters become smaller once the duration of stay in the high-risk phase decreases below the average duration of acute infection. This trend continues, and as the duration of stay in the high-risk phase approaches 0, the rate of transition between risk groups approaches infinity, and so the concept of distinct risk groups becomes meaningless. Consequently, the size distribution of AHI clusters will be that of the homogeneous mixing case (data not shown).

For very high contact-rate ratios, both the prevalence and incidence are maximal when the duration of stay in the high risk phase is just over the average duration of acute infection, which is 2 months. As the contact rate ratio decreases, however, the duration of stay in the high risk phase that generates the maximum incidence increases. This is because the incidence depends on both the number of high-risk susceptibles and the number of high-risk potential transmitters. When the prevalence of infection in the high-risk phase is very high, as it is at high values of the contact rate ratio, the rapid replenishment of high-risk susceptibles due to fairly rapid risk turnover increases the incidence more than the loss of high-risk chronic-stage potential transmitters decreases it. At a lower contact rate ratio, however, the high-risk prevalence is reduced for any given duration of stay. Consequently, the effect of losing a high-risk potential transmitter is increased, while the effect of gaining a high-risk susceptible is diminished. Therefore, the rate of risk turnover at which the maximum incidence occurs is reduced. See Zhang et al. (2012) for a more detailed explanation concerning the prevalence and fraction of acute transmissions.

Results based on the explored parameter ranges

In addition to the cumulative size distribution, we are also interested in how the episodic risk parameters affect the shapes of acute infection outbreaks. As illustrated in the hypothetical systems shown in Fig. 1, acute infection outbreaks of the same size may differ in shape in many ways. The pattern of AHI clustering may reveal whether the AHI transmission chains are mainly sustained by many small and short acute infection outbreaks that are random with no special role in sustaining chains of transmission over time, or are clustered in larger outbreaks. Next, we look into the effect of episodic risk parameters on the various aspects of acute infection outbreaks across a stratified data generated from our individual-based simulations.

To understand the effect of the episodic risk parameters on AIO, we partition the simulated data, first with respect to high-to-low contact rate ratio (rCHL), and then further stratify the data with respect to the values of the transmission potential parameter (X). In order to reduce noise of other model parameters besides durH, we fix the values of the fraction of high-risk population (FrH) and the fraction of high-risk individuals’ contacts made at the high-risk mixing site (FHatH) at 0.1 and 0.9 respectively. In this section, we report results for the data stratified with respect to a high contact rate ratio (rCHL = 30) and X = 0.5. Corresponding results for the homogeneous contact rate (rCH L = 1) and X = 0.5 are given in Appendix ‘C’. Additionally, the box-whisker plots in Appendix ‘C’ give a broader look on the relation of parameters to different measures of outbreak size distribution.

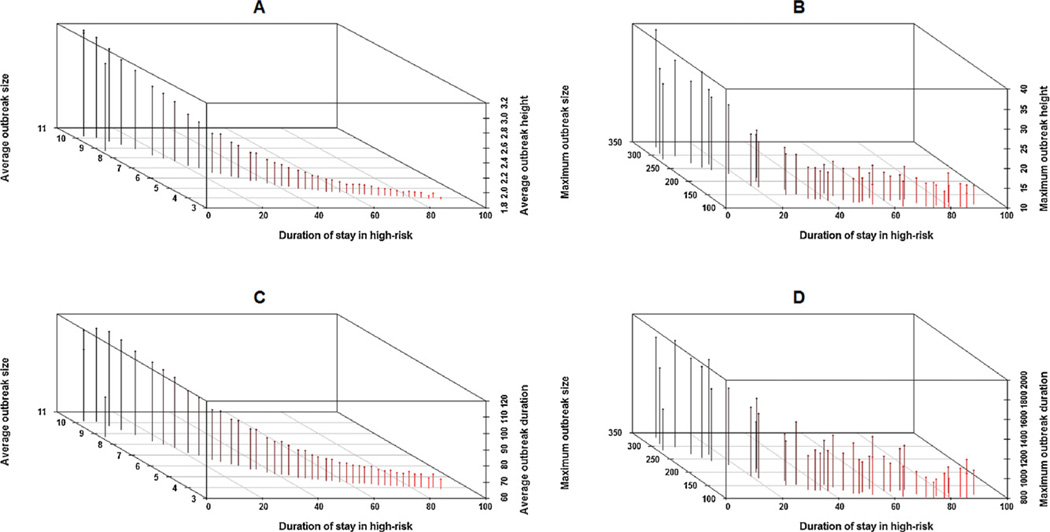
Transmission cluster shapes in addition to cluster sizes might be informative about additional model conformation factors. As introduced in Section “Conceptualizing acute HIV outbreaks”, the height of an acute infection outbreak is the maximum length of a chain of acute transmissions in a cluster. The 3D scatter plots in Panels A and B in Fig. 7 show the relation of average and maximum AIO size and height respectively with respect to the duration of stay in the high-risk phase. As Panels A and B show the size and height of AIO are strongly related to the duration of stay in high-risk (durH) when the other model parameters were kept fixed. Here a high contact rate ratio (rCHL = 30) and a short duration of stay in the high-risk phase results in large size outbreaks as well as longer chains. Both the size and height of AIO drop under slow risk-phase turnover resulting in smaller outbreaks with shorter transmission chains. Risk-phase turnover has a greater effect on the size of the largest acute infection cluster (maximum size of an AIO) as shown in Fig. 7(B). The relationship of the duration (in days) of AIOs with outbreak size (Panels C and D in Fig. 7) follow a similar trend as in Panels A and B under the given parameter settings, which follows from the fact that large outbreaks are more likely to sustain transmission for longer periods in time at the endemic level. A comparison of the trends observed in Fig. 7 with the homogeneous contact ratio case (Fig. C-1 in Appendix ‘C’), shows that AIOs are predominantly small and short regardless of the value of durH parameter when there is no contact rate heterogeneity in the population.

Fig. 7.

3D scatter plots showing the relation of various AHI outbreak measures against the explored range of the ‘duration of stay in high-risk’ for the data stratified with respect to ‘high-to-low contact ratio’: 30 and ‘AHI transmission potential’: 0.5. Panel A: Average outbreak size (Y-axis) versus average outbreak height (Z-axis). Panel B: Maximum outbreak size (Y-axis) versus maximum outbreak height (Z-axis). Panel C: Average outbreak size (Y-axis) versus average outbreak duration (Z-axis). Panel D: Maximum outbreak size (Y-axis) versus maximum outbreak duration (Z-axis).

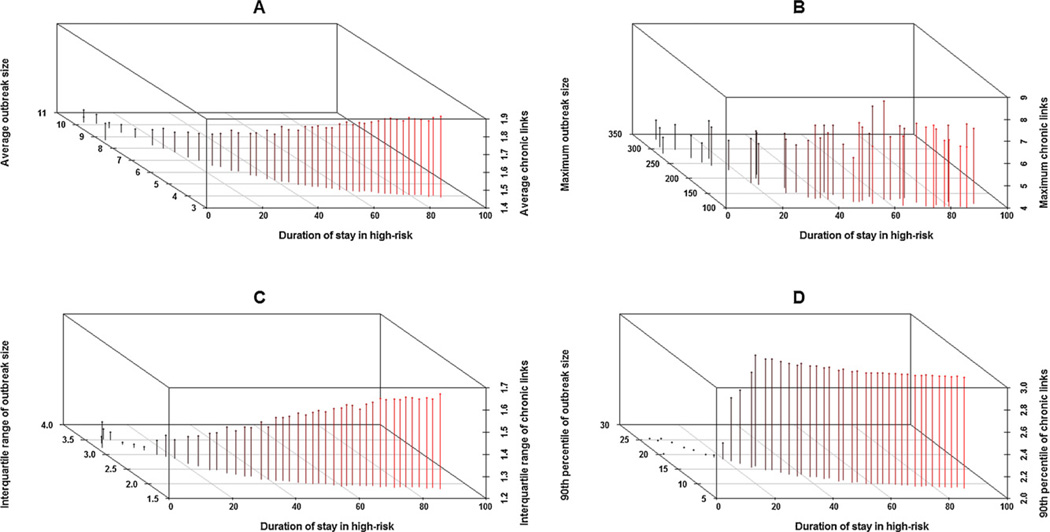
One of the model aspects related to the role of AIOs in sustaining transmission chains is the distribution of chronic transmissions that link acute clusters on transmission chains. For each AIO, we count the number of chronic transmissions that existed between that AIO and its most recent ancestral AIO (if any) on the complete transmission tree. The 3D scatter plots in Fig. 8 show the relation of different summary measures of the distribution of transmissions from chronic infection to respective measures of AIO size. As panels in Fig. 8 show, the number of chronic infection transmissions linking AHI outbreaks is inversely related to the outbreak size, but with some identifiability for the high-risk duration parameter. Where AIOs are large and dominant, we find fewer chronic transmissions linking two AIOS, whereas when AIOs are small and sporadic as in Figure C-2 (in Appendix ‘C’), even when the endemic prevalence is the same, we find an increased role of chronic transmissions is sustaining transmission chains. A higher proportion of chronic transmission link counts that are greater than or equal to 2 indicate a higher proportion of isolates (AIOs of size 1) on the transmission chains. A higher fraction of transmissions from AHI reduces the chances of isolates that are sporadic on the transmission chains and increases the chances of larger and more clustered AHI outbreak clusters on transmission chains.

Fig. 8.

3D scatter plots showing the relation of various AHI outbreak measures against the explored range of the ‘duration of stay in high-risk’ for the data stratified with respect to ‘high-to-low contact ratio’: 30 and ‘AHI transmission potential’: 0.5. X-axis: Duration of stay in high-risk. Panel A: Average outbreak size (Y-axis) versus average chronic links connecting AHI outbreaks (Z-axis). Panel B: Maximum outbreak size (Y-axis) versus chronic links connecting AHI outbreaks (Z-axis). Panel C: Inter-quartile range of outbreak size (Y-axis) versus inter-quartile range of chronic links connecting AHI outbreaks (Z-axis). Panel D: Maximum outbreak size (Y-axis) versus maximum chronic links connecting AHI outbreaks (Z-axis).

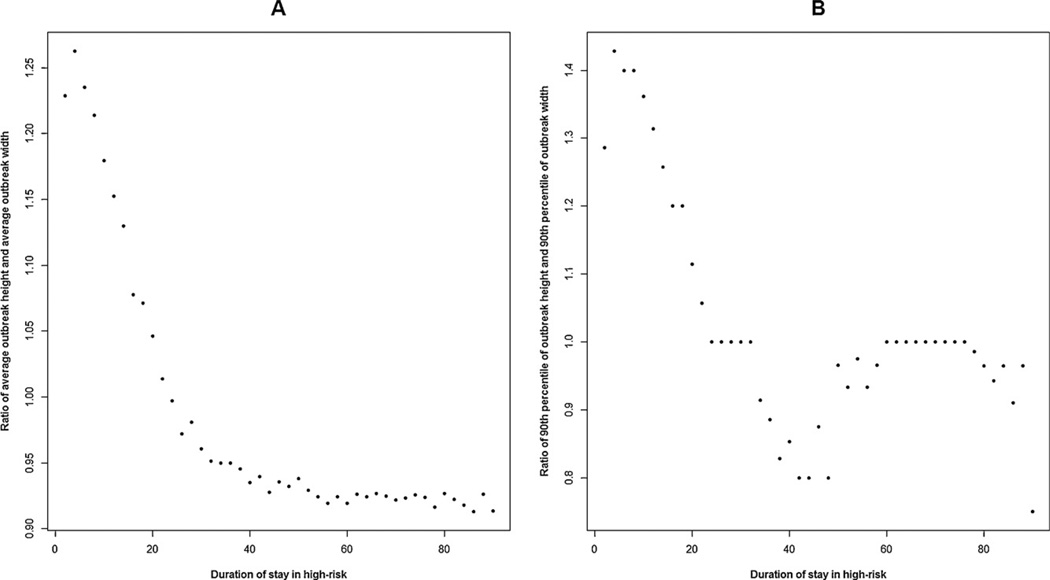
Lastly, Fig. 9 shows plots of two ratios related to AIO tree shapes with respect to the duration of stay in high-risk phase. Panel A presents the ratio of average AIO height and average AIO width, whereas Panel B shows the 90th percentile of the height and width of AIOs respectively. We define width of an AIO as the maximum number of secondary acute infections by an individual member of an AIO. A height-to-width ratio that is greater than 1 implies longer acute chains and a shorter width whereas a ratio that is less than 1 indicates shorter but broader acute infection outbreaks. As mentioned before, a smaller duration of stay in the high-risk phase results in longer AIOs than a longer duration.

Fig. 9.

Scatter plots with the duration of stay in high-risk on the X-axis for the data stratified with respect to ‘high-to-low contact ratio’: 30 and ‘AHI transmission potential’: 0.5. Panel A: Ratio of average outbreak height and average outbreak width. Panel B: Ratio of the 90th percentile of outbreak height and the 90th percentile of outbreak width.

Discussion

Currently, observation of acute infection outbreaks is made though indirect means such as genetic clustering (Brenner et al., 2007, 2011) and phylogenetic relationships (Hughes et al., 2009; Lewis et al., 2008). As reported in Zhang et al. (2012), ‘these analyses indicate that acute infection transmission clusters among MSM could be very common with 64% of early diagnoses being genetically clustered (Brenner et al., 2007)’. Such genetic clusters undoubtedly contain transmission trees that are largely dominated by transmissions during highly contagious AHI, but the dynamics that lead to such clustering have not yet been theoretically explained. The size distribution of acute HIV transmissions trees (or acute infection outbreaks) generated from simulation models may be compared to those observed in the phylogenetic study of genetic sequences in Montreal (Brenner et al., 2011).

In order to understand what information on these key model parameters and/or their interaction might potentially be found in genetic sequence data, the first step is to examine the role of acute infection outbreaks. To do that, we need individual-based models and methods, such as those we have reported in this paper. As a demonstration, we selected a simple model of episodic risk that has been reported in a separate paper (Zhang et al., 2012). Population-level analysis of the key model parameters related to episodic risk presented in this paper helped in clarifying the nature of the transmission dynamics that create a strong link between the episodic risk parameters and the fraction of transmissions by stage of infection.

In our individual-based simulations, we looked into the episodic risk model’s parameters that could have an effect on the fraction of acute transmissions, namely the size distribution of acute infection outbreaks, and the distribution of lengths of chains of acute transmissions. We find that even with a simple model of episodic risk, we find complex interactions between parameters that affect prevalence, AHI transmissions, and tree shapes. Our results suggest that in the episodic risk model, AHI outbreak shapes are most strongly affected by, and therefore most useful in identifying, AHI transmission potential, while other episodic risk parameters may be less identifiable. Still, we observe that higher levels of HIV risk-group turnover tend to give rise to longer chains of transmission. Fast switching of risk behavior links infected individuals belonging to different mixing groups (e.g., high and general mixing sites). Heterogeneity in contact rates leads to a larger size and a longer duration of outbreaks; under a homogeneous contact rate, we find small size outbreaks that are short-lived. Together, risk-group turnover and high contact rate heterogeneity raise the fraction of transmissions from acute infections above the transmission potential and thus lead to an increased number of large size outbreaks with longer chains. As our results show, acute transmission clusters are largest when the duration of stay in the high-risk phase is somewhat longer than the acute state of infection, such that a newly infected high-risk individual stays in the high-risk phase, on average, for the whole duration of his acute infection and a portion of his chronic infection, then transitions to the low-risk phase in order to make room for a new high-risk susceptible who, if infected, will become a new potential acute transmitter. How much longer will depend on the equilibrium fraction of the high risk population that is infected at each duration of stay, which will depend, in turn on the contact-rate ratio, among other factors. The size of the acute clusters decreases as the duration of stay in the high-risk phase becomes shorter than the acute stage. Under extremely fast risk turnover, the size distribution of acute clusters approaches that of acute clusters under a homogeneous mixing setting. We hypothesize that incorporating other aspects of MSM risk behavior, such as higher variability in individual sex act rates and higher volatility in partner pools, is likely to increase the size, duration and connectedness of acute HIV outbreaks.

The analysis presented in this paper is a first step toward understanding patterns of transmission tree size and shape under different mechanisms. The next steps involve looking into the shapes and imbalance of lineage-based trees (Welch, 2011) that are generated from the simulated transmission trees in our individual-based simulations. We are also interested in separates analyses of the distributions of acute outbreaks on ongoing and dead-end chains. Another limitation of our current analysis is the lack of good measures of AHI outbreak shapes. The currently available measures in our Java library are dependent upon the size distribution of AHI outbreaks. Finding suitable measures to understand how the shapes of outbreaks and transmission trees change under different model conformations is non-trivial and is part of our ongoing research. We hope to be able to relate different aspects of tree shapes to different characteristics of the entire infection tree in the studied population. We believe that these methods will complement the coalescent model-based parameter fitting methods from genetic sequences (Volz, 2012).

An important advantage of the individual-based simulation approach is that it allows for the incorporation of many biological and behavioral aspects with a much greater flexibility than is possible with deterministic compartmental models. For example, one of the limitations of our model is that it does not take into account the heterogeneity among the infected individuals in terms of infectiousness or duration of each stage of infection. Both aspects of this limitation are straightforward to address in the context of an individual-based model. For example, the duration of the two stages of infection can be made more flexible in an individual-based model by representing it by a Gamma distribution (see Volz, 2012). We intend to address these and other limitations in our future work.

The complexity of HIV transmission systems can make inference of epidemiologically relevant variables difficult. Consequently, failure to include the necessary complexities may make the inference vulnerable to model misspecification and result in distorted parameter estimates. One way that model misspecification can distort parameter estimates is by causing poor parameter identifiability, which is a common problem when there is poor correspondence between the input variables and output variables, and which results in decreased efficiency of inference from observed data (Jacquez, 1985). Therefore, powerful data, theory, and analysis methods are all needed in order to improve the robustness and identifiability of epidemiologically relevant parameters. In addition, from the data perspective, valid parameter estimation requires not only good genetic and surveillance data, but also good ways to combine them. In addition, good description of patterns related to different factors will help with face validity and inference robustness assessment of parameter estimates.

Good interpretation of what clustered AHI diagnoses imply about pre-exposure prophylaxis (PrEP) or early Test & Treat (T&T) cannot be realized in one single step. First, a model of what generates the clustering needs to be specified. Model parameters quantifying the contributing factors to clustering patterns can be estimated by fitting genetic data to the model. Using the estimated parameters, models with and without PrEP and/or early T&T can be analyzed to explore the possible outcome values. Then, it is necessary to assess how adding a series of realistic aspects to the model (realistically relaxing simplifying assumptions) could change the inferences about PrEP and/or early T&T.

It is important to first explore simple models to find model characteristics with big effects in order to better understand the dynamics underlying HIV transmission, and to better guide prevention. Better estimation of transmission system parameters will be realized by fitting models to combined surveillance and genetic data. Outcome values would help guide how to rank PrEP options among different risk populations. Models validated in this way can also be analyzed with other different control options. For the steps of model specification and making predictions for control decisions, an inference robustness assessment (IRA) strategy is necessary to assure the model used is “as simple as possible, but no simpler” (Koopman, 2005).

Overall, when estimating transmission model parameters from genetic sequence patterns, it may be useful to know what observed tree shapes are generated by what transmission model characteristics. In general, we want to know which infections deserve priority for intensive partner services because they could lead to identifying outbreaks whose control could break ongoing transmission chains.