Abstract
The diffusion of protons through water is understood within the framework of the Grotthuss mechanism, which requires that they undergo structural diffusion in a stepwise manner throughout the water network. Despite long study, this picture oversimplifies and neglects the complexity of the supramolecular structure of water. We use first-principles simulations and demonstrate that the currently accepted picture of proton diffusion is in need of revision. We show that proton and hydroxide diffusion occurs through periods of intense activity involving concerted proton hopping followed by periods of rest. The picture that emerges is that proton transfer is a multiscale and multidynamical process involving a broader distribution of pathways and timescales than currently assumed. To rationalize these phenomena, we look at the 3D water network as a distribution of closed directed rings, which reveals the presence of medium-range directional correlations in the liquid. One of the natural consequences of this feature is that both the hydronium and hydroxide ion are decorated with proton wires. These wires serve as conduits for long proton jumps over several hydrogen bonds.
The mechanism by which protons move through water is at the heart of acid–base chemistry reactions. Understanding the reaction coordinates of this process has been one of the most challenging problems in physical chemistry due to the sheer complexity of water’s hydrogen bond network (1–4). Developing a molecular basis for these phenomena is of great relevance in energy conversion applications such as in the design of efficient fuel cells (5). Over 200 y ago, von Grotthuss proposed a mechanism by which water would undergo electrolytic decomposition (6). He imagined that proton conduction involved the collective shuttling of hydrogen atoms along water wires. The early 20th century found many of the great scientists of the time developing conceptual models to understand the properties of water and its constituent ions (7, 8). Detailed insights into the mechanisms of proton transfer (PT) came much later from a combination of both ab initio molecular dynamics (AIMD) simulations (3, 9–13) and force-field approaches based on the empirical valence bond formalism (14–16). The current textbook picture of the Grotthuss mechanism that has resulted from these studies involves a stepwise hopping of the proton from one water molecule to the next (1, 17, 18). This process occurs on a timescale of 1–2 ps. For a successful transfer, the model requires solvent reorganization around the proton-receiving species to develop a coordination pattern like that of the species it will convert to, a process known as presolvation. In all of these characterizations of the Grotthuss mechanism, the role of the connectivity of the water network was not brought to the forefront (3, 19).
Sometimes PT has also been thought to take on coherent character involving jumps of several protons simultaneously. In this spirit, Eigen (20) suggested that the proton could delocalize over extended hydrogen-bonded wires. There is evidence that this behavior can occur when water molecules form isolated chains, in confined environments like proteins and nanotubes (21–23). In addition, several spectroscopic experiments examining acid–base reactions in ice and water have suggested that fast PT occurs through the formation of transient water wires (24, 25). We have recently shown that, when the hydronium and hydroxide ions approach each other at ∼6 Å, a water wire that always bridges the ions undergoes a collective compression during their recombination (26). This event results in a concerted motion of three protons on the timescale of tens of femtoseconds. It appears as though the formation of polarized water wires is a necessary precursor for correlated PT events. The question then arises whether wire-like structures exist in liquid water and around its constituent ions, and if they do, whether they serve as conduits for different PT mechanisms. Currently, the prevailing view is that concerted PT through proton wires does not occur in liquid water (1, 3, 4, 19, 25).
In this work, we revisit the currently accepted view of the Grotthuss mechanism. Using AIMD simulations of large periodic systems, we find that PT in water occurs over a broader distribution of pathways and timescales than normally assumed. The migration of charge involves bursts of activity along proton wires in the network characterized by the concerted motion of several protons, followed by resting periods that are longer than expected, similar to a jump-like diffusion mechanism. This striking dynamical activity is driven partly by the ability of the proton wires to undergo collective compressions. Understanding the structural origins of this behavior, requires a refined picture of the 3D hydrogen bond network. Our inspiration comes from the results of previous studies where it was observed that liquid water is characterized by a broad distribution of closed rings (27–29). In all of these studies, the directionality of the hydrogen bonds in the network has been ignored. By including this feature within our analysis of the rings, we reveal striking medium-range directional correlations in the network. One of the important consequences of this feature is that proton wires naturally decorate the atmosphere of the ions and subsequently influence the mechanisms by which they diffuse through water.
The Grotthuss Mechanism Revisited
We begin first by examining the range of both the spatial and temporal activity of the proton and hydroxide ion in the network.
The Excess Proton in Water.
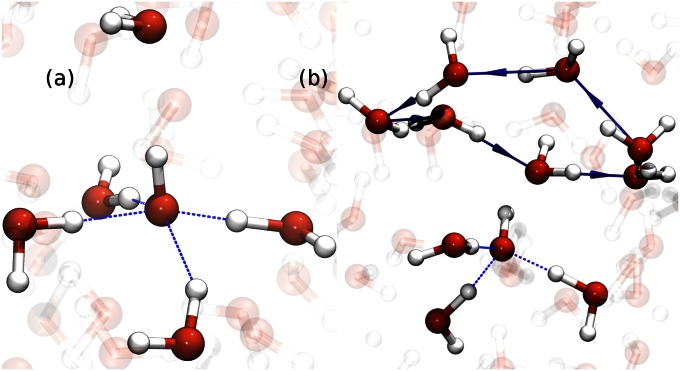
The accepted picture of PT requires that the proton moves from one water molecule to the next in a stepwise manner throughout the network. We find instead that proton wires surrounding the hydronium, gives the proton more spatial activity. Stepwise PT events between two water molecules occur during resting periods, although these typically do not contribute to the long-range migration of the proton. The majority of successful PT events propagate through the wires in a quasiconcerted manner over two to three water molecules with a stronger tendency for double jumps. It should be emphasized that these correlated hopping events are distinct from Zundel-to-Zundel transfers that were suggested in earlier studies (30). An important factor that allows for these correlated jumps is that they are strongly coupled to the collective compressions of the wires as seen in Fig. 1 similar to what was observed during the recombination of hydronium and hydroxide (26). The textbook descriptions of the Grotthuss mechanism paint a picture of all of the protons in the ensemble diffusing with a similar mechanism. We find instead that, rather than undergoing an exclusive stepwise hopping, the proton goes through periods of bursts in activity, where it can jump 4–8 Å in distance over several water molecules on the subpicosecond timescale, followed by fairly long resting spells. An example of this burst-and-rest behavior is shown in Fig. 2A. The reader is referred to SI Appendix for other examples illustrating this feature. In any AIMD simulation, the sensitivity of the results to choice of basis set and density functional is always a concern. We have ascertained that this feature of collective compressions and subsequent correlated PTs that occur, are independent of these factors (SI Appendix). In our benchmarks, we have also ascertained that these features are not sensitive to finite box size effects as they occur in both 64 and 128 water systems. In both cases, the Bjerrum length where electrostatic correlations become critical, is approximately one-half the magnitude of the box side length and thus does not interfere significantly with the creation of directed rings around the proton, which serve as the pathways for PT.
Fig. 1.
The average of the symmetrized PT coordinates for pairs of consecutive PT events (double PT jumps) on the x axis vs. the collective compression of the wire on the y axis. On the x axis,  and
and 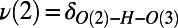 are the symmetrized PT coordinates defined as the difference in distance of the transferring proton along the hydrogen bond [
are the symmetrized PT coordinates defined as the difference in distance of the transferring proton along the hydrogen bond [ and
and  ]. The species O(1), O(2), and O(3) are consecutive oxygen atoms along a wire that house the proton at some point during PT. Associated with each PT coordinate is the distance between the oxygen atoms along the wire:
]. The species O(1), O(2), and O(3) are consecutive oxygen atoms along a wire that house the proton at some point during PT. Associated with each PT coordinate is the distance between the oxygen atoms along the wire:  ,
,  , and the y axis shows the sum of these two distances. This plot is strikingly similar to the “banana” plots in the stepwise PT jumps (9). Here, instead double jumps are facilitated by collective compressions (see SI Appendix for similar plot for the extent of correlations in groups of triple PT events).
, and the y axis shows the sum of these two distances. This plot is strikingly similar to the “banana” plots in the stepwise PT jumps (9). Here, instead double jumps are facilitated by collective compressions (see SI Appendix for similar plot for the extent of correlations in groups of triple PT events).
Fig. 2.
(A) Burst and rest behavior of the proton is shown for one trajectory. On the y axis, we show the distance that the proton jumps with respect to a reference starting point at the beginning of the trajectory. The motion of the proton goes through periods of bursts where it can jump rather long distances due to correlated proton hopping followed by resting periods. The regions labeled B indicate points where there is a burst in activity and R are regimes where the proton is going through a resting period. (B) Proton history correlation function (44) [ , where h is 1 when a tagged species in the system is a proton or 0 if it is not] is shown for individual proton species in the system as well as the ensemble average. The two blue curves, for example, illustrate two limiting cases involving a trapped proton and a very short-lived proton transiently formed during concerted PT events. The red, green, and violet curves shown, interpolate between these two limiting cases. The black curve represents the average over all PT events from different trajectories, whereas the dashed magenta curve is a fit to this average using several exponentials.
, where h is 1 when a tagged species in the system is a proton or 0 if it is not] is shown for individual proton species in the system as well as the ensemble average. The two blue curves, for example, illustrate two limiting cases involving a trapped proton and a very short-lived proton transiently formed during concerted PT events. The red, green, and violet curves shown, interpolate between these two limiting cases. The black curve represents the average over all PT events from different trajectories, whereas the dashed magenta curve is a fit to this average using several exponentials.
An instructive way of seeing the broad range of timescales associated with PT is through the history correlation function  , which essentially describes the probability that a tagged species that was a proton at
, which essentially describes the probability that a tagged species that was a proton at  , would be a proton at some time t after (see Fig. 2 legend for a detailed definition). The average
, would be a proton at some time t after (see Fig. 2 legend for a detailed definition). The average  (Fig. 2B, black curve) requires more than two exponentials and thus reflects the multidynamical behavior of PT. Furthermore, the
(Fig. 2B, black curve) requires more than two exponentials and thus reflects the multidynamical behavior of PT. Furthermore, the 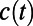 (black curve) does not decay to zero on the simulated timescales, which indicates that there appears to be longer relaxation processes controlling PT. Besides this feature, there also appears to be enormous variability in the decay dynamics of the individual
(black curve) does not decay to zero on the simulated timescales, which indicates that there appears to be longer relaxation processes controlling PT. Besides this feature, there also appears to be enormous variability in the decay dynamics of the individual  . This is because the proton does not propagate through the entire water network in a uniform way: for example, there are some cases where the proton is trapped for
. This is because the proton does not propagate through the entire water network in a uniform way: for example, there are some cases where the proton is trapped for  ps, whereas in other situations, very short-lived protons form on the femtosecond timescale during correlated back-and-forth jumps. Part of the slow time relaxation behavior in the
ps, whereas in other situations, very short-lived protons form on the femtosecond timescale during correlated back-and-forth jumps. Part of the slow time relaxation behavior in the  originates from the presence of these fairly long-lived traps. Some of this behavior can be seen in the work of Voth and coworker (31), which was however interpreted within the framework of a stepwise PT mechanism.
originates from the presence of these fairly long-lived traps. Some of this behavior can be seen in the work of Voth and coworker (31), which was however interpreted within the framework of a stepwise PT mechanism.
The multidynamical nature of PT has important implications in how we interpret the mechanistic origins of the femtosecond dynamics and diffusion constant of the proton. First, the motions on the femtosecond timescale do not exclusively involve the proton rattling between two waters as this is the same timescale over which protons can move in a correlated fashion over several water molecules (32, 33). Second, an analysis of the mean square displacement of the proton from our simulations suggests that the effective diffusion constant of the proton, although perhaps fortuitously close to the experimental value, can originate from a mixture of processes involving fairly long-lived trapped protons and concerted proton hopping events over several waters (SI Appendix).
The Hydroxide Ion in Water.
Historically, the Grotthuss mechanism has been discussed mostly within the context of the motion of the excess proton in water. However, it is also well appreciated that the mobility of hydroxide ions exceeds what one would predict from hydrodynamic theories (3). Similar to the proton, the motion of the hydroxide ion is believed to exclusively involve stepwise hopping events accompanied by solvent reorganization. Our AIMD simulations, however, reveal a lot more activity in the hydrogen bond network. The hydroxide ion shares some common features to the proton. In particular, we find that its successful migration is dominated by correlated jumps involving two to three proton “holes” (SI Appendix). In some of these events, the hydroxide undergoes an initial triple jump resulting in a concerted motion of three protons, followed by one of the holes receding. This results in an effective jump length of two hydrogen bonds. From a dynamical point of view, the  for the hydroxide is also characterized by decay dynamics that cannot be fit by less than two exponentials. This behavior arises from the heterogeneity in the type of motion that it undergoes in different solvent environments as we will now discuss. Like the proton, the hydroxide moves through the network in a manner that does not involve small continuous movements, but rather large jumps followed by periods of rest.
for the hydroxide is also characterized by decay dynamics that cannot be fit by less than two exponentials. This behavior arises from the heterogeneity in the type of motion that it undergoes in different solvent environments as we will now discuss. Like the proton, the hydroxide moves through the network in a manner that does not involve small continuous movements, but rather large jumps followed by periods of rest.
In contrast to the excess proton, periods of rest also appear to be more sensitive to the details of the hydrogen bonding from both the accepting and donating side of the hydroxide ion. In some instances, we observe that periods of rest are associated with the hydroxide ion accepting four hydrogen bonds in a square planar arrangement (Fig. 3A). However, activity involving motion of the proton hole can be coupled to periods where the hydroxide ion accepts three hydrogen bonds. This picture is quite similar to the currently held view of the role of presolvation (3), with the caveat of course that in our simulations we observe a broader distribution of jumps of the proton hole.
Fig. 3.
A illustrates the hypercoordinated hydroxide, which accepts four hydrogen bonds and donates one weaker hydrogen bond. B illustrates the undercoordinated hydroxide ion, which accepts three hydrogen bonds while the donating hydrogen bond is left dangling pointing to a closed ring.
Resting spells of the hydroxide ion can also come from other types of variation in the hydrogen bond network. The hydroxide ion tends to donate a weak hydrogen bond to a water molecule in the surrounding network. It turns out that the presence of an undercoordinated hydroxide ion (one that accepts three hydrogen bonds) does not necessarily guarantee that it will be in a more active state. We find instead that there can also be resting periods for undercoordinated hydroxide ions. The feature that makes this entity somewhat unique is that its donating hydrogen bond is dangling and hence points to a small cavity (Fig. 3B). It is interesting to note that a similar type of behavior has been observed in hexagonal ice Ih, where Buch and coworker (34) showed that interstitial or off-lattice hydroxide ions can serve as traps. To the best of our knowledge, this is the first time that this stable configuration of the hydroxide ion has been observed in liquid water.
Structural Origins of Proton Wires
Up to this point, we have shown that both the proton and hydroxide move through the network in a manner that yields a broader range of possible jump lengths and timescales than currently assumed. The task at hand now is to rationalize the origin of this multiscale and multidynamical behavior.
Ring Statistics: Water, Proton, and Hydroxide.
The pioneering studies by Rahman and Stillinger (29) showed that liquid water was made up of a distribution of closed rings. Studies that followed built on this picture to characterize the 3D hydrogen bond network of liquid water (27, 28). Similar to these studies, we also find that water is characterized by a broad distribution of rings of different sizes with a tendency for rings made up of five to seven water molecules (see SI Appendix for a more detailed review of previous studies). However, if one is interested in how the ions perturb the network and in a probe of the pathways in their vicinity, a more spatially local description of the rings is required. One measure of this is the distribution of rings that individually thread water molecules. In neat water, the average number of rings around a water molecule is ∼13. However, this property exhibits significant fluctuations ranging between ∼3 and ∼25 rings (SI Appendix). As a point of reference, in hexagonal ice, each water molecule is always surrounded by a fixed number of 12 rings.
One of the ways in which the ions perturb the network compared with pure liquid water is by altering the distribution of rings that thread them. The hydronium typically participates in a fewer number of rings, whereas the opposite is true for the hydroxide ion (SI Appendix). This reflects the relative hydrophobic and hydrophilic character of the hydronium and hydroxide oxygen, respectively. Furthermore, both ions also reduce the fluctuations in the number of rings due to the electrostatic field that they impose on the network. Besides the number of rings, the geometry of the ions also alter the relative proportion of rings of different sizes threading them compared with neat water (SI Appendix). Earlier in our report, we showed that the motion of the proton involved periods of fairly long traps. Although the underlying PT reaction coordinate will be strongly coupled to the degree to which collective compressions occur in the vicinity of the proton, the ring distributions provide some clues into the origins of the strong variation in resting times. One of the factors that controls the extent of trapping is that water molecules participating in different numbers of rings confer different stability to the proton. If one embraces the notion of tetrahedral water threaded by rings that fluctuate on similar timescales as PT, it is not so surprising that there would be some variability in stabilizing the proton in different regions of the network. In particular, regions of the water network characterized by a lower number of rings appear to be sites for longer trapping (greater than 5 ps). However, regions where there are a larger number of rings appear to serve as shorter traps for the proton (less than 2 ps). These features are illustrated in Fig. 4.
Fig. 4.
This figure shows distribution of the total number of rings for protons in long-lived (blue) vs. short-lived (green) traps illustrated using a clustered bar chart. The blue bars tend to be larger at smaller ring values (less than  ), whereas the green bars tend to be larger at larger ring values (greater than
), whereas the green bars tend to be larger at larger ring values (greater than  ).
).
Medium-Range Directional Correlations.
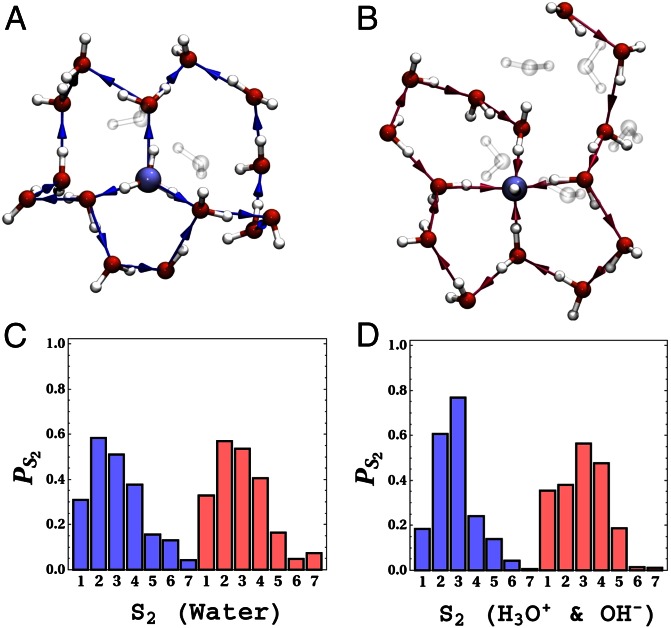
In the previous discussion, the directionality of the hydrogen bonds within the rings is not taken into consideration. This feature turns out to be critical in characterizing the network environment of the proton and hydroxide ion. It is instructive to motivate the ensuing results by first looking at the directed rings in neat water, which are characterized by rather striking topological patterns. For example, a ring can form a closed wire as seen in Fig. 5A where each water in the ring donates and accepts a single hydrogen bond with its neighbors in the ring. This type of water molecule will be referred to as a DA water within the ring. This arrangement can be broken by the introduction of a water molecule that is a double donor (DD) or double acceptor (AA) (as seen in Fig. 5B). Note that the presence of the closed-ring topology forces a DD molecule in a ring to be always accompanied by an AA one (this is a consequence of a lemma in graph theory: Handshaking Lemma for Directed Graphs) regardless of the size or shape of the ring. As we will soon see, it turns out that the hydronium and hydroxide ion play the role of DD and AA, respectively, for the great majority of rings threading them. The local medium-range directional correlations in the water network are strongly coupled to the number of DD–AA pairs in the ring. It is important to stress that the rings shown in Fig. 5, although illustrated as clusters for clarity, are topological structures that exist within a thermal bath of liquid water.
Fig. 5.
A and B show  for two directed six-membered rings, and C shows the distribution of
for two directed six-membered rings, and C shows the distribution of  obtained for neat water. When
obtained for neat water. When  (A), the ring is made up of only DA water molecules, whereas when
(A), the ring is made up of only DA water molecules, whereas when 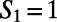 , the ring consists of one DD, one AA, and four DA water molecules. The blue-colored paths show possible realizations of
, the ring consists of one DD, one AA, and four DA water molecules. The blue-colored paths show possible realizations of  obtained for these rings. In particular for the
obtained for these rings. In particular for the  ring, the longest outgoing path from the tagged DA water (surrounded by a blue sphere) to waters other than itself, is shown by the blue path that is made of five hydrogen bonds. This path ends at the water surrounded by a yellow sphere. For
ring, the longest outgoing path from the tagged DA water (surrounded by a blue sphere) to waters other than itself, is shown by the blue path that is made of five hydrogen bonds. This path ends at the water surrounded by a yellow sphere. For  (B), a realization of the longest outgoing wire for a DD water molecule (surrounded by a blue sphere) is shown by the blue path made up of three hydrogen bonds. This path ends at the water surrounded by the yellow sphere. For clarity, in these figures we only show examples of six-membered rings. However, as discussed in the text, the same features hold for rings of all sizes. The distributions of
(B), a realization of the longest outgoing wire for a DD water molecule (surrounded by a blue sphere) is shown by the blue path made up of three hydrogen bonds. This path ends at the water surrounded by the yellow sphere. For clarity, in these figures we only show examples of six-membered rings. However, as discussed in the text, the same features hold for rings of all sizes. The distributions of  of charged systems are quite similar (SI Appendix).
of charged systems are quite similar (SI Appendix).
To quantify these directional correlations within the ring, we introduce the order parameters  and
and  (see Materials and Methods, Computational Methods, for details).
(see Materials and Methods, Computational Methods, for details).  measures the number of DD–AA pairs in a ring. For example, Fig. 5 A and B illustrates an
measures the number of DD–AA pairs in a ring. For example, Fig. 5 A and B illustrates an  and
and  directed ring, respectively. Under the current simulated thermodynamic conditions, the value of
directed ring, respectively. Under the current simulated thermodynamic conditions, the value of  varies between 0 and 3 with the greatest tendency of finding a single DD–AA pair with
varies between 0 and 3 with the greatest tendency of finding a single DD–AA pair with  (Fig. 5C). Intuitively, the dominant
(Fig. 5C). Intuitively, the dominant  motif seen in Fig. 5B forms a building block that allows for the formation of an infinitely spanning 3D hydrogen bond network which would not be achieved if the balance was tipped in favor of rings dominated by
motif seen in Fig. 5B forms a building block that allows for the formation of an infinitely spanning 3D hydrogen bond network which would not be achieved if the balance was tipped in favor of rings dominated by  ,
,  , or
, or  . As
. As  increases from 0 (Fig. 5A) to 1 (Fig. 5B), the presence of the DD–AA pair alters the ability to traverse the ring via a continuous sequence of hydrogen bonds. Thus, the relative proportion of DD, AA, and DA waters within the rings induces very characteristic directional correlations in the network.
increases from 0 (Fig. 5A) to 1 (Fig. 5B), the presence of the DD–AA pair alters the ability to traverse the ring via a continuous sequence of hydrogen bonds. Thus, the relative proportion of DD, AA, and DA waters within the rings induces very characteristic directional correlations in the network.
The presence of these correlations leads to a broad distribution of hydrogen bond pathways leading into and out of a water molecule. Our order parameter  probes these pathways by looking at the longest among all shortest directed paths that come into or out of a water molecule or an ion within a particular ring. Fig. 5 A and B, for example, illustrates in dark blue the path yielded by
probes these pathways by looking at the longest among all shortest directed paths that come into or out of a water molecule or an ion within a particular ring. Fig. 5 A and B, for example, illustrates in dark blue the path yielded by  for the
for the 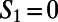 and
and 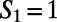 ring, respectively. The directed paths along these rings can be thought of as medium-range water wires in the 3D hydrogen bond network. Although the presence of continuous sequences of hydrogen bonds may not come as much of a surprise, understanding their statistical properties in terms of the presence of closed directed water rings has not been previously appreciated. For meaningful comparison, because the hydronium and hydroxide ion dominantly play the role of DD and AA respectively, we compare their distribution of
ring, respectively. The directed paths along these rings can be thought of as medium-range water wires in the 3D hydrogen bond network. Although the presence of continuous sequences of hydrogen bonds may not come as much of a surprise, understanding their statistical properties in terms of the presence of closed directed water rings has not been previously appreciated. For meaningful comparison, because the hydronium and hydroxide ion dominantly play the role of DD and AA respectively, we compare their distribution of 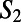 to only DD and AA water molecules in neat water. By imposing a bias on the distribution of rings around each ion, the directed pathways that surround them are also perturbed. These distributions, shown in Fig. 6C for neat water, and Fig. 6D for the ions, show that the relative proportion of wires consisting of two to four hydrogen bonds are quite different. Earlier, we showed that there appears to be some correlation between the ring statistics and proton trapping. If we consider the directionality of the rings and compare the distribution of
to only DD and AA water molecules in neat water. By imposing a bias on the distribution of rings around each ion, the directed pathways that surround them are also perturbed. These distributions, shown in Fig. 6C for neat water, and Fig. 6D for the ions, show that the relative proportion of wires consisting of two to four hydrogen bonds are quite different. Earlier, we showed that there appears to be some correlation between the ring statistics and proton trapping. If we consider the directionality of the rings and compare the distribution of  for long- and short-lived protons, we observe that the relative proportion of directed wires between two to four hydrogen bonds exhibits some differences (SI Appendix). Trapping behavior of the hydroxide appears to be more complicated. In particular, trapped states for the hydroxide are sensitive to not only the number rings threading the ion but also their ability to form a ring with
for long- and short-lived protons, we observe that the relative proportion of directed wires between two to four hydrogen bonds exhibits some differences (SI Appendix). Trapping behavior of the hydroxide appears to be more complicated. In particular, trapped states for the hydroxide are sensitive to not only the number rings threading the ion but also their ability to form a ring with  . Although the trapped state of the hydroxide that accepts only three hydrogen bonds has a lower number of rings threading it, an
. Although the trapped state of the hydroxide that accepts only three hydrogen bonds has a lower number of rings threading it, an  ring cannot form in this state due to the rather peculiar solvent environment in its vicinity (Fig. 3B).
ring cannot form in this state due to the rather peculiar solvent environment in its vicinity (Fig. 3B).
Fig. 6.
The upper panels show snapshots of the environment of the H3O+ (A) and OH− (B) ions, which is made of closed rings. For clarity, not all of the rings threading the ions are shown. Wires along the rings are also shown around each ion. Note that the OH− ion accepts four hydrogen bonds and donates a weak hydrogen bond in this case. As mentioned in the text, the H3O+ acts as a DD water in the ring, whereas the OH− acts as an AA for the majority of the rings they participate in. The figure illustrates that both the H3O+ and OH− are characterized by many outgoing and incoming wires, respectively. C and D compare the distribution of 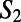 for neat water [DD (blue) and AA (red)], H3O+ (blue), and OH− (red) systems.
for neat water [DD (blue) and AA (red)], H3O+ (blue), and OH− (red) systems.
The picture that begins to emerge is that the one has to view the hydronium and hydroxide ion as fluxional topological structures of a collective coordinate involving the hydrogen bond network and not just a few water molecules solvating the ion. In particular, because of the presence of medium-range directional correlations in the network, the center of excess charge acts as a “source” for multiple pathways radiating out of it (Fig. 6A). In contrast, the hydroxide ion acts as a “sink” for many directed hydrogen bond wires bridging from the bulk into the center of negative charge (Fig. 6B).
Network Coordinates of PT.
The results presented until this point demonstrate that one of the origins of the rich dynamical activity of the proton and hydroxide ion stems from the complex network architecture of liquid water. It follows somewhat naturally that the broad distribution of directed pathways around the ions must lead to a hierarchy of collective modes involving the rings and hence wires. These modes involve collective compressions and expansions, which turn out to be critical in facilitating correlated PT as we showed earlier. This correlated proton hopping does not persist throughout the network in an uninterrupted fashion. Besides the compressions, solvent fluctuations around the proton play an important role in facilitating PT. It is beyond the scope of the current study to provide a quantitative description of all of the network coordinates involved in PT. However, by viewing water as a 3D network composed of fluctuating directed rings, we obtain some clues into the collective nature of PT as a reorganization of the network. One component of this involves the restructuring of the hydrogen bond network through the interconversion of rings of different sizes. Large-amplitude rotational and translational modes of water molecules in the vicinity of the proton, similar to those seen previously in bulk water (35), result in the breakage and formation of rings (Fig. 7A). These fluctuations obviously lead to changes in both  and
and  and subsequently perturb the wires surrounding the hydronium and either trap or release it from different parts of the network. This may or may not lead to long-range transfer of the proton because one has to distinguish between proton activity along wires locally threading the hydronium and slower longer range translocation of the proton, which requires motion from one ring to another. Within this context, another striking feature that can change the environment of the hydronium is its umbrella inversion mode. This motion changes the pyramidal shape of the hydronium and moves its oxygen atom between different parts of the water network (Fig. 7B). Due to the heterogeneity of the surrounding environment caused by the variation in the size and shape of different rings, the barrier for PT is quite sensitive to changes the inversion mode induces on the hydronium and can thus either facilitate or hinder the propagation of the proton. More details of the role of ring interconversion and the umbrella inversion mode on PT will be reported in a forthcoming study.
and subsequently perturb the wires surrounding the hydronium and either trap or release it from different parts of the network. This may or may not lead to long-range transfer of the proton because one has to distinguish between proton activity along wires locally threading the hydronium and slower longer range translocation of the proton, which requires motion from one ring to another. Within this context, another striking feature that can change the environment of the hydronium is its umbrella inversion mode. This motion changes the pyramidal shape of the hydronium and moves its oxygen atom between different parts of the water network (Fig. 7B). Due to the heterogeneity of the surrounding environment caused by the variation in the size and shape of different rings, the barrier for PT is quite sensitive to changes the inversion mode induces on the hydronium and can thus either facilitate or hinder the propagation of the proton. More details of the role of ring interconversion and the umbrella inversion mode on PT will be reported in a forthcoming study.
Fig. 7.
A illustrates how the interconversion of rings, in this case a five- and seven-membered ring, result in concerted PT. On the y axis, the symmetrized PT coordinates for the concerted PT events,  ,
, 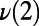 , and
, and 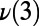 (corresponding to the black, red, and green curves, respectively) are shown. (B) Coupling between the ring interconversions and the umbrella inversion mode of the hydronium during PT events. The data series shows the umbrella inversion mode coordinate on the y axis along with four snapshots from the molecular dynamics trajectory. The purple triangle is formed by the base of three protons, which is used to illustrate the role of the inversion mode. The inversion coordinate is defined by the perpendicular distance between the oxygen atom of the hydronium ion and the plane formed by the hydrogen atoms. In the first example (A), the inversion mode does not change and hence does not play a role in the PT. However, in the second example, the inversion mode changes, which facilitated the formation and breakage of a 4M ring and is coupled to PT. For clarity, we note that in the first 2 ps the oxygen lies below the triangular blue base, whereas between 2 and 6 ps the oxygen lies above the triangular base.
(corresponding to the black, red, and green curves, respectively) are shown. (B) Coupling between the ring interconversions and the umbrella inversion mode of the hydronium during PT events. The data series shows the umbrella inversion mode coordinate on the y axis along with four snapshots from the molecular dynamics trajectory. The purple triangle is formed by the base of three protons, which is used to illustrate the role of the inversion mode. The inversion coordinate is defined by the perpendicular distance between the oxygen atom of the hydronium ion and the plane formed by the hydrogen atoms. In the first example (A), the inversion mode does not change and hence does not play a role in the PT. However, in the second example, the inversion mode changes, which facilitated the formation and breakage of a 4M ring and is coupled to PT. For clarity, we note that in the first 2 ps the oxygen lies below the triangular blue base, whereas between 2 and 6 ps the oxygen lies above the triangular base.
Conclusion
In conclusion, we have shown here using first-principles simulations that the motion of protons through the water network is a complex process involving the collective behavior of both structural and dynamical properties of the network. The presence of proton wires gives proton motion much broader spatial and temporal character compared with the current textbook description of the Grotthuss mechanism (17). One way to picture this is to imagine the proton moving through a free-energy landscape along a generalized PT coordinate. Rather than experiencing the same effective barrier for PT throughout the water network, our results seem to suggest that the free-energy surface is very rough and characterized by basins of varying depths and activation barriers. The details of this surface will also be affected by nuclear quantum effects (NQEs), which are known to enhance the delocalization of the proton along the hydrogen bond, as observed in previous studies (9, 10). It is quite likely that NQEs will serve to further enhance the delocalization of the proton in the hydrogen bond network as well as increase the correlated hopping of the protons. Quantifying this behavior is underway in our group.
The phenomena we report here should open up new challenges for both experimentalists and theoreticians working on problems involving acid–base chemistry. In particular, our observations should be useful in shedding light on the complexity behind the origin of the time-dependent infrared dynamics of the proton and hydroxide (32, 33). Furthermore, it should also open up interesting discussions for those engaged in understanding PT in ice where phenomena such as proton trapping have also been observed (36). Besides its implications on PT on aqueous systems, the phenomena we observe bear similar features to important biological systems. In particular, collective vibrations have recently been recognized as playing a possible role in promoting hydrogen transfer in enzymes (37), which is crucial for catalysis. In addition, the fundamental aspects raised in this report are likely to open up new directions in the role of the water network in phenomena associated with the hydration of ions (38) and macromolecules such as proteins and DNA.
Materials and Methods
Computational Methods.
AIMD simulations of all of the aqueous systems were conducted using Quickstep, which is part of the CP2K package (39). In these calculations, ab initio Born–Oppenheimer molecular dynamics is used for propagation of the classical nuclei. A convergence criterion of  a.u. was used for the optimization of the wave function. Using the Gaussian and plane waves method, the wave function was expanded in the Gaussian double zeta with valence polarization functions (DZVP) basis set. An auxiliary basis set of plane waves was used to expand the electron density up to a cutoff of 300 Ry. We used the BLYP (the exchange correction of Becke and the correlation function of Lee, Yang and Parr) gradient correction (40) to the local density approximation and Goedecker–Teter–Hutter pseudopotentials for treating the core electrons (41). Sensitivity of results with respect to choice of basis set and density functional is always a concern in ab initio simulations. It is well known that current generalized gradient approximation functionals tend to overstructure water. In a previous study on the recombination of the hydronium and hydroxide (26), we ascertained that the mechanisms inferred in that study, in particular the collective compression and concerted motion of the protons, observed using the Perdew, Burke, and Ernzerhof (PBE)-DZVP combination, was reproduced when we used a larger basis set (PBE-TZV2P) or another density functional (HCTH/120-DZVP). Furthermore, this result also appears to be independent of finite-box size effects. The reader is referred to SI Appendix for more details on these benchmarks. Similar strategies were used to identify the proton and hydroxide and their respective solvation shells as in our previous work (26). All systems simulated consist of a box of side length 15.6404 Å with 128 water molecules for the neutral system (with either a proton or hydroxide ion for the charged systems). Simulations were conducted within the constant size, volume and temperature ensemble at 300 K using the canonical-sampling velocity-rescaling thermostat (42).
a.u. was used for the optimization of the wave function. Using the Gaussian and plane waves method, the wave function was expanded in the Gaussian double zeta with valence polarization functions (DZVP) basis set. An auxiliary basis set of plane waves was used to expand the electron density up to a cutoff of 300 Ry. We used the BLYP (the exchange correction of Becke and the correlation function of Lee, Yang and Parr) gradient correction (40) to the local density approximation and Goedecker–Teter–Hutter pseudopotentials for treating the core electrons (41). Sensitivity of results with respect to choice of basis set and density functional is always a concern in ab initio simulations. It is well known that current generalized gradient approximation functionals tend to overstructure water. In a previous study on the recombination of the hydronium and hydroxide (26), we ascertained that the mechanisms inferred in that study, in particular the collective compression and concerted motion of the protons, observed using the Perdew, Burke, and Ernzerhof (PBE)-DZVP combination, was reproduced when we used a larger basis set (PBE-TZV2P) or another density functional (HCTH/120-DZVP). Furthermore, this result also appears to be independent of finite-box size effects. The reader is referred to SI Appendix for more details on these benchmarks. Similar strategies were used to identify the proton and hydroxide and their respective solvation shells as in our previous work (26). All systems simulated consist of a box of side length 15.6404 Å with 128 water molecules for the neutral system (with either a proton or hydroxide ion for the charged systems). Simulations were conducted within the constant size, volume and temperature ensemble at 300 K using the canonical-sampling velocity-rescaling thermostat (42).
Graph Topology Generation.
The rings were constructed using the shortest path ring definition (43), which considers a water molecule (using the oxygen atoms as centers) and two of its nearest neighbors with a distance cutoff criterion of 3.3 Å. This cutoff corresponds to the end of the first hydration shell given by the g(r) in BLYP water. Subsequently, the shortest path passing through these three molecules is used to generate a cyclic ring. Directed edges are inserted between pairs of nodes in the ring, which reflects the direction of the hydrogen bonds. The direction of the hydrogen bond along the edge consisting of nodes  and
and  was determined by finding the hydrogen
was determined by finding the hydrogen  that yields the shortest hydrogen bond:
that yields the shortest hydrogen bond:  …
… , where
, where 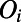 and
and  are covalently bonded. For simplicity, in constructing the order parameters described below, every pair of nodes in the ring is assigned an edge. Although this inserts an edge along hydrogen bonds that would be considered as broken by standard criteria, we have checked that this feature does not affect the properties we have determined in this work (see SI Appendix for more details). The order parameters
are covalently bonded. For simplicity, in constructing the order parameters described below, every pair of nodes in the ring is assigned an edge. Although this inserts an edge along hydrogen bonds that would be considered as broken by standard criteria, we have checked that this feature does not affect the properties we have determined in this work (see SI Appendix for more details). The order parameters  and
and  are defined below:
are defined below:
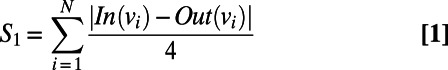 |
In the expression for  above, N refers to the number of nodes in a ring (for a hexamer, this would be 6).
above, N refers to the number of nodes in a ring (for a hexamer, this would be 6).  is the in-degree of a node on the graph which quantifies the number of ingoing edges to that node, whereas
is the in-degree of a node on the graph which quantifies the number of ingoing edges to that node, whereas  is the out-degree of a node on the graph, which quantifies the number of outgoing edges from the node. For example, a water molecule that is a DD in the ring would have an out-degree of 2 and an in-degree of 0 (vice versa for an AA), whereas a DA water would have both an out-and-in degree of 0 within the ring. In
is the out-degree of a node on the graph, which quantifies the number of outgoing edges from the node. For example, a water molecule that is a DD in the ring would have an out-degree of 2 and an in-degree of 0 (vice versa for an AA), whereas a DA water would have both an out-and-in degree of 0 within the ring. In  ,
, 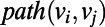 , corresponds to the length of the shortest path between a node
, corresponds to the length of the shortest path between a node  and
and 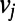 , whereas
, whereas  picks up the longest among all possible paths leading out of
picks up the longest among all possible paths leading out of  . For paths leading into
. For paths leading into 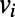 , the role of the subscripts i and j are simply reversed.
, the role of the subscripts i and j are simply reversed.
Supplementary Material
Acknowledgments
The authors acknowledge Meher Prakash, Matteo Salvagglio, and Michele Ceriotti for useful discussions. The authors thank Swiss National Supercomputing Center (CSCS) and High Performance Computing Group of ETH Zurich for computational resources. Financial support from the European Union Grant ERC-2009-AdG-247075 is gratefully acknowledged. T.D.K. acknowledges financial support from the Graduate School of Excellence MAINZ and the Inverse Design mit definierten Eigenschaften (IDEE) project of the Carl Zeiss Foundation.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
See Commentary on page 13697.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1306642110/-/DCSupplemental.
References
- 1.Agmon N. The Grotthuss mechanism. Chem Phys Lett. 1995;244(5-6):456–462. [Google Scholar]
- 2.James T. Hynes. Physical chemistry: The protean proton in water. Nature. 1999;397(6720):565–567. [Google Scholar]
- 3.Marx D, Chandra A, Tuckerman ME. Aqueous basic solutions: Hydroxide solvation, structural diffusion, and comparison to the hydrated proton. Chem Rev. 2010;110(4):2174–2216. doi: 10.1021/cr900233f. [DOI] [PubMed] [Google Scholar]
- 4.Knight C, Voth GA. The curious case of the hydrated proton. Acc Chem Res. 2012;45(1):101–109. doi: 10.1021/ar200140h. [DOI] [PubMed] [Google Scholar]
- 5.Kreuer KD, Paddison SJ, Spohr E, Schuster M. Transport in proton conductors for fuel-cell applications: Simulations, elementary reactions, and phenomenology. Chem Rev. 2004;104(10):4637–4678. doi: 10.1021/cr020715f. [DOI] [PubMed] [Google Scholar]
- 6.de Grotthuss CJT. 1806. Sur la décomposition de l’eau et des corps qu’elle tient en dissolution à l’aide de l’électricité galvanique [On the decomposition of water and of solutes by electrical currents]. Ann Chim (Paris) LVIII:54–74. French.
- 7.Bernal JD, Fowler RH. A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions. J Chem Phys. 1933;1(8):515–548. [Google Scholar]
- 8.Eigen M, DeMaeyer L. Self-dissociation and protonic charge transport in water and ice. Proc R Soc Lond. 1958;A247(1251):505–533. [Google Scholar]
- 9.Marx D, Tuckerman ME, Hutter J, Parrinello M. The nature of the hydrated excess proton in water. Nature. 1999;397:601–604. [Google Scholar]
- 10.Tuckerman ME, Marx D, Parrinello M. The nature and transport mechanism of hydrated hydroxide ions in aqueous solution. Nature. 2002;417(6892):925–929. doi: 10.1038/nature00797. [DOI] [PubMed] [Google Scholar]
- 11.Geissler PL, Dellago C, Chandler D, Hutter J, Parrinello M. Autoionization in liquid water. Science. 2001;291(5511):2121–2124. doi: 10.1126/science.1056991. [DOI] [PubMed] [Google Scholar]
- 12.Tuckerman M, Laasonen K, Sprik M, Parrinello M. Ab initio molecular dynamics simulation of the solvation and transport of H3O+ and OH− ions in water. J Phys Chem. 1995;99(16):5749–5752. [Google Scholar]
- 13.Tuckerman M, Laasonen K, Sprik M, Parrinello M. Ab initio molecular dynamics simulation of the solvation and transport of hydronium and hydroxyl ions in water. J Chem Phys. 1995;103(1):150–161. [Google Scholar]
- 14.Voth GA. Computer simulation of proton solvation and transport in aqueous and biomolecular systems. Acc Chem Res. 2006;39(2):143–150. doi: 10.1021/ar0402098. [DOI] [PubMed] [Google Scholar]
- 15.Knight C, Maupin CM, Izvekov S, Voth GA. Defining condensed phase reactive force fields from ab-initio molecular dynamics simulations: the case of the hydrated excess proton. J Chem Theory Comput. 2010;6(10):3223–3232. doi: 10.1021/ct1004438. [DOI] [PubMed] [Google Scholar]
- 16.Markovitch O, et al. Special pair dance and partner selection: Elementary steps in proton transport in liquid water. J Phys Chem B. 2008;112(31):9456–9466. doi: 10.1021/jp804018y. [DOI] [PubMed] [Google Scholar]
- 17.Atkins P, de Paula J. Physical Chemistry. 8th Ed. Oxford, UK: Oxford Univ Press; 2006. [Google Scholar]
- 18.Marx D. Proton transfer 200 years after von Grotthuss: Insights from ab initio simulations. ChemPhysChem. 2007;8(2):209–210. doi: 10.1002/cphc.200600128. [DOI] [PubMed] [Google Scholar]
- 19.Berkelbach TC, Lee HS, Tuckerman ME. Concerted hydrogen-bond dynamics in the transport mechanism of the hydrated proton: A first-principles molecular dynamics study. Phys Rev Lett. 2009;103(23):238302. doi: 10.1103/PhysRevLett.103.238302. [DOI] [PubMed] [Google Scholar]
- 20.Eigen M. Proton transfer, acid-base catalysis, and enzymatic hydrolysis. Part I: Elementary processes. Angew Chem Int Ed Engl. 1964;3(1):1–19. [Google Scholar]
- 21.Cui Q, Karplus M. Is a “proton wire” concerted or stepwise? A model study of proton transfer in carbonic anhydrase. J Phys Chem B. 2003;107(4):1071–1078. [Google Scholar]
- 22.Dellago C, Naor MM, Hummer G. Proton transport through water-filled carbon nanotubes. Phys Rev Lett. 2003;90(10):105902. doi: 10.1103/PhysRevLett.90.105902. [DOI] [PubMed] [Google Scholar]
- 23.Cao Z, et al. Mechanism of fast proton transport along one-dimensional water chains confined in carbon nanotubes. J Am Chem Soc. 2010;132(33):11395–11397. doi: 10.1021/ja1046704. [DOI] [PubMed] [Google Scholar]
- 24.Timmer RLA, Cox MJ, Bakker HJ. Direct observation of proton transfer in ice Ih using femtosecond spectroscopy. J Phys Chem A. 2010;114(5):2091–2101. doi: 10.1021/jp908561h. [DOI] [PubMed] [Google Scholar]
- 25.Cox MJ, Timmer RL, Bakker HJ, Park S, Agmon N. Distance-dependent proton transfer along water wires connecting acid–base pairs. J Phys Chem A. 2009;113(24):6599–6606. doi: 10.1021/jp9004778. [DOI] [PubMed] [Google Scholar]
- 26.Hassanali A, Prakash MK, Eshet H, Parrinello M. On the recombination of hydronium and hydroxide ions in water. Proc Natl Acad Sci USA. 2011;108(51):20410–20415. doi: 10.1073/pnas.1112486108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Belch AC, Rice SA. The distribution of rings of hydrogen-bonded molecules in a model of liquid water. J Chem Phys. 1987;86(10):5676–5682. [Google Scholar]
- 28.Matsumoto M, Baba A, Ohmine I. Topological building blocks of hydrogen bond network in water. J Chem Phys. 2007;127(13):134504. doi: 10.1063/1.2772627. [DOI] [PubMed] [Google Scholar]
- 29.Rahman A, Stillinger FH. Hydrogen-bond patterns in liquid water. J Am Chem Soc. 1973;95(24):7943–7948. [Google Scholar]
- 30.Vuilleumier R, Borgis D. Transport and spectroscopy of the hydrated proton: A molecular dynamics study. J Chem Phys. 1999;111(9):4251–4266. [Google Scholar]
- 31.Izvekov S, Voth GA. Ab initio molecular-dynamics simulation of aqueous proton solvation and transport revisited. J Chem Phys. 2005;123(4):044505. doi: 10.1063/1.1961443. [DOI] [PubMed] [Google Scholar]
- 32.Woutersen S, Bakker HJ. Ultrafast vibrational and structural dynamics of the proton in liquid water. Phys Rev Lett. 2006;96(13):138305. doi: 10.1103/PhysRevLett.96.138305. [DOI] [PubMed] [Google Scholar]
- 33.Roberts ST, et al. Observation of a Zundel-like transition state during proton transfer in aqueous hydroxide solutions. Proc Natl Acad Sci USA. 2009;106(36):15154–15159. doi: 10.1073/pnas.0901571106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Cwiklik L, Buch V. Hydroxide trapped in the interior of ice: A computational study. Phys Chem Chem Phys. 2009;11(9):1294–1296. doi: 10.1039/b820031a. [DOI] [PubMed] [Google Scholar]
- 35.Laage D, Hynes JT. A molecular jump mechanism of water reorientation. Science. 2006;311(5762):832–835. doi: 10.1126/science.1122154. [DOI] [PubMed] [Google Scholar]
- 36.Singer SJ, Knight C. Hydrogen-Bond Topology and Proton Ordering in Ice and Water Clusters. New York: Wiley; 2011. pp. 1–74. [Google Scholar]
- 37.Hay S, Scrutton NS. Good vibrations in enzyme-catalysed reactions. Nat Chem. 2012;4(3):161–168. doi: 10.1038/nchem.1223. [DOI] [PubMed] [Google Scholar]
- 38.Marcus Y. Effect of ions on the structure of water: Structure making and breaking. Chem Rev. 2009;109(3):1346–1370. doi: 10.1021/cr8003828. [DOI] [PubMed] [Google Scholar]
- 39.VandeVondele J, et al. QUICKSTEP: Fast and accurate density functional calculations using a mixed gaussian and plane waves approach. Comput Phys Commun. 2005;167:103–128. [Google Scholar]
- 40.Lee C, Yang W, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys Rev B Condens Matter. 1988;37(2):785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 41.Goedecker S, Teter M, Hutter J. Separable dual-space Gaussian pseudopotentials. Phys Rev B Condens Matter. 1996;54(3):1703–1710. doi: 10.1103/physrevb.54.1703. [DOI] [PubMed] [Google Scholar]
- 42.Bussi G, Donadio D, Parrinello M. Canonical sampling through velocity rescaling. J Chem Phys. 2007;126(1):014101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- 43.Donadio D, Raiteri P, Parrinello M. Topological defects and bulk melting of hexagonal ice. J Phys Chem B. 2005;109(12):5421–5424. doi: 10.1021/jp050690z. [DOI] [PubMed] [Google Scholar]
- 44.Luzar A, Chandler D. Hydrogen-bond kinetics in liquid water. Nature. 1996;379:55–57. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.