Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Aug 28;3:2519. doi: 10.1038/srep02519

Recurrent connections form a phase-locking neuronal tuner for frequency-dependent selective communication

Dongkwan Shin 1, Kwang-Hyun Cho 1,a
PMCID: PMC3755292  PMID: 23981983

Abstract

The brain requires task-dependent interregional coherence of information flow in the anatomically connected neural network. However, it is still unclear how a neuronal group can flexibly select its communication target. In this study, we revealed a hidden routing mechanism on the basis of recurrent connections. Our simulation results based on the spike response model show that recurrent connections between excitatory and inhibitory neurons modulate the resonant frequency of a local neuronal group, and that this modulation enables a neuronal group to receive selective information by filtering a preferred frequency component. We also found that the recurrent connection facilitates the successful routing of any necessary information flow between neuronal groups through frequency-dependent resonance of synchronized oscillations. Taken together, these results suggest that recurrent connections act as a phase-locking neuronal tuner which determines the resonant frequency of a local group and thereby controls the preferential routing of incoming signals.

The brain consists of numerous subregions responsible for specialized functions, and these subregions constitute an anatomically connected network. Most brain functions require the flexible and rapid reorganization of brain networks in response to behavioral, cognitive, or perceptual demands. Recent studies have revealed the formation of dynamic and flexible functional brain networks during cognitive or perceptual tasks1,2,3,4,5,6, selective attention7,8,9, and working memory10. A question then arises as to how a neuronal group selects its communication targets to realize dynamic and flexible communication. Previous studies have suggested that neuronal communication between different brain areas is mediated by coherence of oscillating neuronal activity in each area2,3,11,12,13,14. However, the underlying mechanism for selective communication still remains unclear.

Synchronized oscillations are ubiquitously found in the brain and they seem to coordinate various brain activities at multiple spatial scales, ranging from microscopic neural circuits to macroscopic brain networks. Previous studies have shown that the synchronization of oscillatory behaviors between distributed regions plays an important role in selective attention, cognitive function, memory, and neuronal communication15,16,17. Synchronized oscillations are known to originate from rhythmic neuronal firing caused by interactions between excitatory and inhibitory neurons18. A generic neural circuit consists of two major cell types, excitatory principal neurons and inhibitory interneurons, and they form three types of recurrent connections through chemical synapses: mutual excitation between excitatory principal neurons (E-E), mutual inhibition between inhibitory interneurons (I-I), and recurrent inhibition through an excitatory-inhibitory loop (E-I). Recurrent excitatory connections, such as E-E and I-I, form a positive feedback loop, while recurrent inhibitory connections constitute a negative feedback loop. The frequency of synchronized oscillations is primarily determined by network topology. For instance, E-I feedback loops generate gamma oscillations, whereas I-I feedback loops promote high-frequency oscillations19,20,21,22. Moreover, it was revealed that local neuronal assemblies with recurrent connections tend to oscillate with a characteristic frequency, and show resonance phenomena in response to a preferred stimulus23,24,25. Taken together, previous studies suggest that the different types of recurrent connections might have a significant influence on the formation of a functional brain network for a given stimulus, and that the modification of recurrent connections might contribute to selective and flexible communication between distant neuronal groups.

In this study, we hypothesize that the combination of different types of recurrent connections in a local neuronal group has a crucial role in tuning the resonant frequency of the group and consequently enables the flexible and selective configuration of neural networks. To examine this hypothesis, we employed the spike response model (SRM) and simulated a spiking neural network composed of recurrent connections that represents a local neuronal group26. Through extensive computational simulations with varying synaptic weights and connectivity ratios, we found that a neuronal group composed of feedback loops has a topology-dependent resonant frequency, and that this resonant frequency is differently modulated by E-E and I-I feedback loops. It was also found that a neuronal group can switch its communication targets by tuning the resonant frequency, which suggests that the resonant synchronized oscillation and its modulation by recurrent connections might be a fundamental mechanism underlying the dynamic and flexible formation of neural networks.

Results

Large-scale simulations were carried out with a spiking neural network model composed of excitatory (E) and inhibitory (I) neurons based on the SRM. All network structures considered in this study contain recurrent connections among E- and I- neurons that form positive (E-E and I-I) or negative (E-I) feedback loops (see Methods for details on network architectures).

Synchronized oscillations generated by negative feedback loops between E- and I-cells

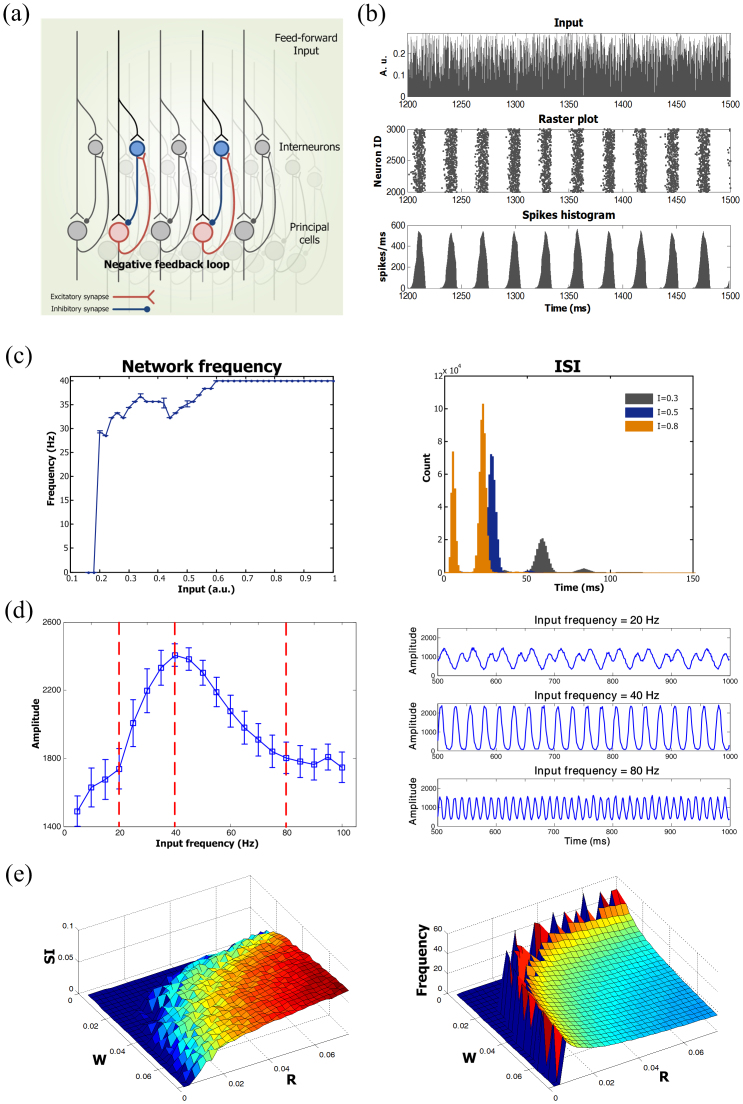
Negative feedback loops between excitatory and inhibitory neurons are ubiquitously found in cortical networks and hippocampal subnetworks (e.g., DG, CA1, and CA3), and such structures have been proposed to contribute to generating oscillatory behaviors in local networks27,28,29. To investigate the oscillatory behavior generated by negative feedback loops, an excitatory-inhibitory recurrent network was constructed, composed of randomly selected pairs of E- and I-neurons with the connection probability R and the synaptic weight W (Fig. 1(a)). In response to white noise input ranging from 0 to 0.3 (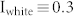Inline graphic), excitatory neurons showed a synchronized oscillation with a frequency of 34.5 Hz (Fig. 1(b)), whereas the interspike interval (ISI) distribution showed that individual neurons fired with a period of about 60 ms, corresponding to 16.7 Hz (Fig. 1(c), right). As the input signal increased, ISI distributions narrowed, and the position of the peak approached the period of the network frequency (40 Hz), indicating that more neurons participated synchronously in generating the synchronized oscillation. This network frequency was conserved even when the input (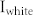Inline graphic) was varied over a range between 0.6 and 1.0, which confirms that this synchronized oscillation generated by E-I recurrent connections is an emergent property arising from the network topology (Fig. 1(c), left). We further investigated how a local neuronal group responds to external oscillating inputs with varying input frequency and obtained the output amplitude versus input frequency plot (Fig. 1(d)). The neuronal group that has the spontaneous frequency of 40 Hz tends to oscillate with a larger amplitude at the input frequency of 40 Hz compared to 20 or 80 Hz (Fig. 1(d), right), indicating that the spontaneous frequency can be referred to as the ‘resonant frequency' of a neuronal group.

Figure 1. Synchronized oscillation and resonant frequency of negative feedback structures.

Figure 1

Open in a new tab

(a) Diagram of E-I negative feedback connectivity showing feed-forward external input (black), excitatory synapses of principal cells (red), and inhibitory synapses of interneurons (blue). (b) Raster plot of output spikes (middle) and output firing rate (bottom) of excitatory neurons evoked by white random noise input (top). (c) Network frequency as a function of input amplitude (left) and interspike interval (ISI) distributions for various input amplitudes (right). Note that the cutoff value of 0.16 in the left figure is the minimal input for the firing of a neuron (see Supplementary Fig. S1(a)). The highest ISI peak for each input represents the leading period of the synchronized oscillation. The first ISI peak for I = 0.8 shows a very fast oscillation caused by burst firing within one cycle of network oscillations (see Supplementary Fig. S1(b)). Network parameters were as follows: R = W = 0.025 and d = 3 ms. (d) The amplitude of synchronized oscillation as a function of input frequency (left), and the temporal profiles for input frequencies of 20, 40, and 80 Hz (right). Network parameters were the same as (c), and various combinations of oscillating inputs (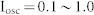Inline graphic) and white noise inputs (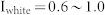Inline graphic) were considered (n = 100, error bars represent the s.e.). (e) Synchronized index (left) and resonant frequency (right) as a function of R and W for I = 0.8 (see Methods for details on the computation of SI and resonant frequency).

To further investigate how E-I couplings influence the synchronized oscillations of neuronal groups, the synchronization index (SI) and network frequency were measured by varying the connectivity ratio and the strength of the synaptic weight. The SI was based on the autocorrelogram for phase synchrony30 modified for population synchrony (see Methods for details). Perfect synchronization occurs when all excitatory neurons periodically fire at the same time, and low synchronization happens when most neurons fire incoherently. As E-I recurrent connections were strengthened, the population of excitatory neurons exhibited more synchronous oscillation patterns and lower resonant frequencies (Fig. 1(e)). For low R and W, the activity of neurons correlated little with each other, and therefore they fired independently, resulting in an unsynchronized oscillation (see Supplementary Notes and Fig. S2(a)). As R and W increased, excitatory neurons started to synchronize with other neurons. The network frequency of the synchronized oscillation decreased with increasing R and W (Fig. 1(e)). Such enhanced synchronization and decreased network frequency are driven by inhibitory neurons that take the initiative in generating a rhythmic pattern. Since inhibitory neurons receive both external input and signals from excitatory neurons, they strongly and rhythmically suppress excitatory neurons. This strong and rhythmical modulation of excitatory neurons makes excitatory neurons fire synchronously, which leads to strong synchronization and low network frequencies. However, when R and W exceed certain levels, excitatory neurons abruptly stop to fire and thereby show no oscillatory behavior because inhibitory neurons strongly suppress excitatory neurons (Fig. S2(b)). We excluded such a regime as it is out of scope of this study. Consequently, it turns out that the negative feedback structure between E- and I-neurons has its own resonant frequency determined by the network topology, such as the connectivity ratio and the synaptic weight.

Network frequency modulation by mutual excitation and inhibition

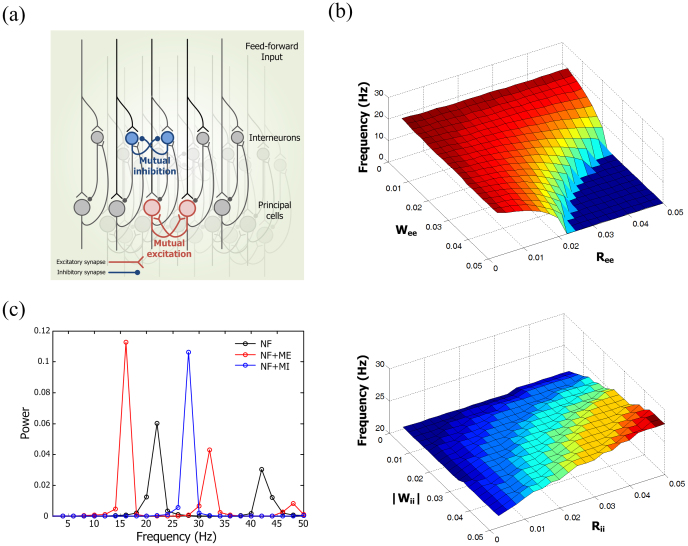
A simple negative feedback circuit in biological networks has the potential to generate sustained oscillations. Intriguingly, it is known that positive feedback loops coupled to such a negative feedback oscillator contribute to adjusting the frequency of a negative feedback oscillator while maintaining its amplitude31. In addition, our previous study showed that two types of positive feedback loops in cellular systems, PP (Positive-Positive) and NN (Negative-Negative), have different roles in regulating the synchronization of negative feedback oscillators32. On the basis of these findings, we hypothesize that two types of positive feedback loops, mutual excitation (ME) and mutual inhibition (MI), may have different roles in modulating the resonant frequency of negative feedback (NF) structures, and that these different modulations may control information flow between neuronal groups. To examine this hypothesis, we investigated how ME and MI regulate the resonant frequency of negative feedback structures. An NF network model was constructed, composed of E-I connections with R = W = 0.05, such that it had a resonant frequency f ~ 21 Hz. 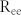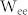When MEs were introduced by increasing Inline graphic and Inline graphic, the resonant frequency of the NF network decreased (Fig. 2(b), top). 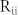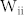By contrast, the resonant frequency increased when Inline graphic and Inline graphic of mutual inhibitions increased (Fig. 2(b), bottom). Such different modulations of the resonant frequency can be explained by competition between excitatory and inhibitory neurons. Mutual excitation prolongs positive phases of excitatory neurons against the influence of inhibitory neurons, leading to a lengthened cycle of synchronized oscillation. On the other hand, mutual inhibition enhances the power of inhibitory neurons and therefore rapidly resets the phases of excitatory neurons, which increases the resonant frequency. These different modulations of the resonant frequency by positive feedback loops were evident in the oscillation power spectrum (Fig. 2(c)). In addition to the NF network, two more networks were considered: the NF network with MEs (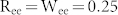Inline graphic), and that with MIs (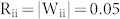Inline graphic). Each network showed one strong peak at f = 16, 21, and 28 Hz, confirming that mutual excitation and inhibition modulate the resonant frequency of the negative feedback structure in different ways. This tendency was maintained over a large range of synaptic delays, suggesting that the different modulation of resonant frequency by mutual excitation and inhibition is conserved across structures (see Supplementary Notes and Fig. S3).

Figure 2. Different modulation of resonant frequency by ME and MI.

Figure 2

Open in a new tab

(a) Diagram of E-I negative feedback structures coupled with mutual excitation (red) and inhibition (blue). (b) Modulation of the resonant frequency by increasing the connectivity ratio and the synaptic weight of E-E couplings (top) and I-I couplings (bottom). Highly interconnected excitatory neurons greatly increased the network activity and thereby induced a hyperexcitable state. The frequency of this state was set to 0 Hz (blue region in top). Parameters used were R = W = 0.05 for the E-I negative feedback network. (c) Power spectrum of synchronized oscillations for NF, NF with ME, and NF with MI networks. Parameters used were R = W = 0.05 for NF, 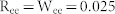Inline graphic for ME, and 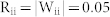Inline graphic for MI couplings.

Resonant synchronized oscillations in response to an oscillatory input

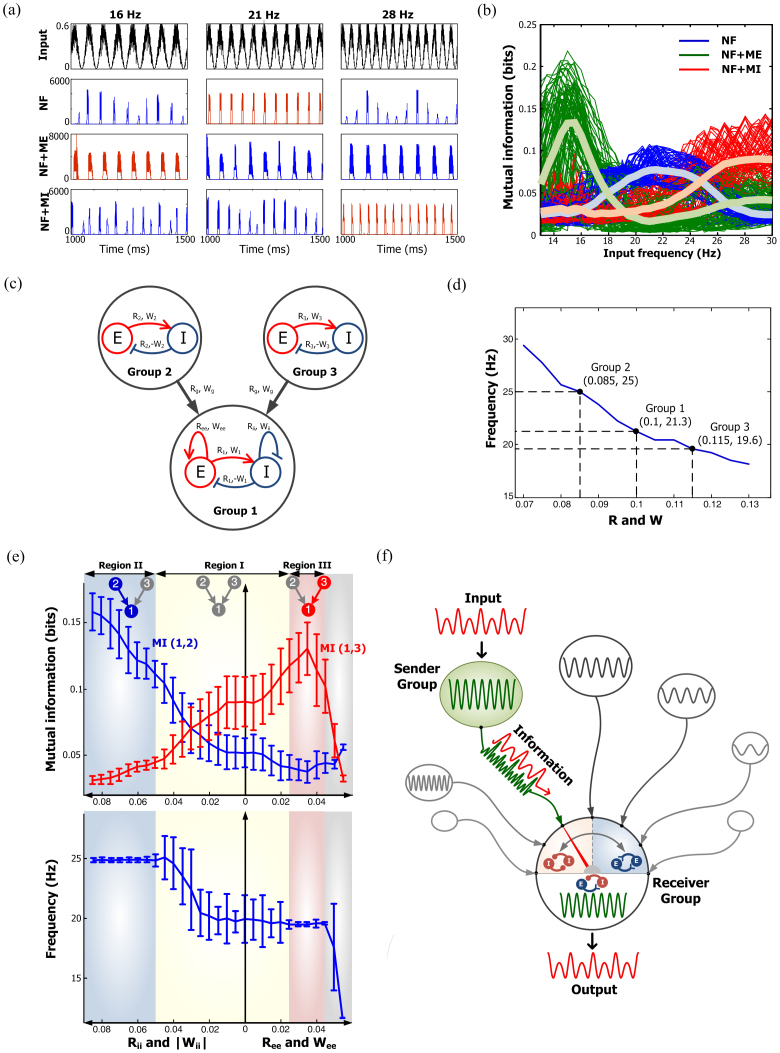
To further investigate how a local neuronal group responds to an external oscillating input, a sinusoidally oscillating input was applied with three different frequencies, f = 16, 21, and 28 Hz, to the aforementioned networks. Each network preferentially responded to the oscillating input having the same frequency as its resonant frequency (Fig. 3(a)). All of these resonant synchronized oscillations were phase-locked to the input oscillations and were very stable, which suggests that this resonance might be essential for robust and accurate information transfer. For the non-resonant input frequency, on the other hand, resulting oscillations were not uniform and the output oscillation frequency was not related to either the input frequency or the resonant frequency. Such irregular patterns of resulting oscillations are evidently not appropriate for any meaningful information processing due to the signal instability. To examine the shared information between input and output oscillations, the input frequencies were varied (f = 13 ~ 30 Hz) and the corresponding mutual information was measured. Various oscillating inputs with different amplitudes were considered, ranging from 0.16 to 1.0, and all of the responses obtained from the three networks were investigated. Mutual information increased near the resonant frequency of each network (Fig. 3(b)), indicating that a neuronal group composed of recurrent connections can operate as a band-pass filter allowing only preferred information to be transferred. Taking these findings into account, we conclude that a neuronal group composed of feedback structures has a certain resonant frequency and can select preferred information by rewiring the network topology and tuning the resonant frequency.

Figure 3. Frequency-dependent selective communication.

Figure 3

Open in a new tab

(a) Spike histograms of NF, NF with ME, and NF with MI networks in response to oscillating inputs. Parameters used for these three networks were the same as those of Fig. 2(c). Each network shows a resonant synchronized oscillation (red) when the input frequency is close to the resonant frequency of the network. The blue color indicates non-resonant oscillations. (b) Mutual information between oscillating inputs and resultant oscillations of three networks as a function of input frequency. Various combinations of oscillating inputs (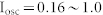Inline graphic) and white noise inputs (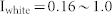Inline graphic) were considered. White lines denote the average values over 100 combinatorial inputs. (c) Two sender groups and one receiver group. Each group is composed of E-I negative feedback loops with different connectivity ratios (R1/2/3) and synaptic weights (W1/2/3). Group 1 has additional recurrent connections, such as ME, and MI. Rg and Wg denote the connectivity ratio and the synaptic weight of global synapses from sender groups to a receiver group, respectively. Further details on network structures and inputs are described in Methods. (d) Resonant frequencies of three groups. Network parameters were determined as R1/2/3 and W1/2/3, such that each group had a distinct resonant frequency 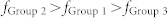Inline graphic. (e) Frequency modulation (bottom) and mutual information between Group 1 and Groups 2 or 3 (top) mediated by mutual excitation and inhibition. Initially, Group 1 without mutual excitation nor inhibition received less information from both sender groups (Region I). 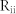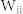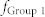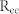Mutual information between Groups 1 and 2 (blue) increased with the increase of Inline graphic and Inline graphic, since Inline graphic is close to Inline graphic (Region II). 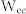By contrast, as Inline graphic and Inline graphic increase, 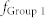Inline graphic gets close to 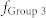Inline graphic (Region III), resulting in the maximal mutual information between Groups 1 and 3 (red). (f) Schematic diagram illustrating a neuronal tuner for frequency-dependent selective communication between neuronal groups. The gauge needle (colored in red) in a receiver group points to the resonant frequency, which is tuned by E-E and I-I couplings. Adjusting the frequency to one of the sender groups opens a communication channel (green) that information can flow through the channel (red).

Frequency-dependent selective communication

Based on the foregoing results, we postulate that a neuronal group operating as a band-pass filter can select its communication target group by changing the recurrent connectivity. To examine this, we first generated three different neuronal groups composed of E-I negative feedback loops (Fig. 3(c)). Different values of R and W were chosen for each group, such that each one had a distinct resonant frequency, 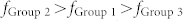Inline graphic, as shown in Fig. 3(d). All neurons in Groups 2 and 3 had constant input currents with random Gaussian variations, and all neurons in Group 1 had signaling inputs from the excitatory neurons in Groups 2 and 3. To determine the synaptic efficacy from Groups 2 or 3 to Group 1, it was assumed that there was reliable signal propagation, without signal failure or explosions, from a sender group to a receiver group. To achieve such stable signal propagation, a spike gain representing the ratio of the average number of neurons firing in a sender group and that in a receiver group should be near unity when the avalanche model is applied33,34. Hence, we determined the synaptic weight, Wg ~ 0.0016, while keeping Rg = 1 for simplicity (see Supplementary Notes and Fig. S4). All of the details on the network architectures are described in Methods.

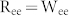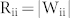Next, it was investigated whether selective communication can be achieved by modulating mutual excitation and inhibition. We varied the connectivity ratio and the synaptic weight of mutual excitation or inhibition, and set Inline graphic and Inline graphic for simplicity. 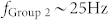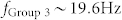In response to an input signal, excitatory neurons of Groups 2 and 3 showed oscillatory activity with the resonant frequencies of Inline graphic and Inline graphic, respectively. When these signals from the sender groups were delivered to Group 1, the output frequency of Group 1 could be modulated by additional recurrent connections (Fig. 3(e), bottom). Adding mutual inhibition raised the oscillation frequency of Group 1 to that of Group 2, 25 Hz. In this case (Region II in Fig. 3(e)), the mutual information between Group 1 and 2, MI(1,2), was significantly higher than MI(1,3), which indicates that Group 1 can open a communication channel from Group 2 and concurrently block the channel from Group 3. On the contrary, an increase in mutual excitation in Group 1 shifted the oscillation frequency of Group 1 to that of Group 3, ~19 Hz, which approaches Region III, where resonant synchronized oscillations between Groups 1 and 3 were strongly enhanced. In Region I, however, the oscillation frequency of Group 1 was highly variable across random trials. In other words, Group 1 could not produce reliable synchronized oscillations for between-area communication. Moreover, both MI(1,2) and MI(1,3) were relatively too small to open a communication channel, which implies that Region I represents the ‘OFF' state for communication. These findings demonstrated that recurrent excitation facilitates selective communication by tuning the resonant frequency. This suggests that recurrent excitation in neural networks is an essential building block for selective communication and, consequently, might play a role as a neuronal tuner that determines the characteristic frequency of a local neuronal group and controls information flow (Fig. 3(f)).

Discussion

We have described a novel mechanism by which distant neuronal groups communicate selectively and flexibly with each other. The routing mechanism suggested in this study has two important implications. First, neuronal communication through resonant synchronized oscillations allows distributed neuronal assemblies to form a coherent functional brain network. Since resonance-based communication is more stable than a simple gating mechanism based on a “detailed balance” scheme35, the proposed mechanism is suitable for reliable signal transduction and information transfer in a functional brain network. Second, recurrent connections such as mutual excitation and inhibition within a neuronal group modulate the resonant frequency, which permits selective and flexible communication. A recurrent connection in a functional brain network can be considered as a radio tuner that adjusts a radio frequency to a preferred radio station to receive desired information. In other words, the recurrent connection modulates the resonant frequency and keeps a communication channel open to receive any necessary information (Fig. 3(f)).

Recent studies have proposed routing mechanisms based on a detailed balance scheme35 or band-pass filtering36 using a simple feed-forward structure. Such a detailed balance mechanism provides one possible way for a receiver group to selectively extract a target signal from multiple inputs by disturbing the balance between excitatory and inhibitory synaptic activity. Akam et al. introduced an oscillatory gating mechanism with which band-pass filtering can be achieved by a simple network consisting of excitatory and inhibitory neurons that exploits a network-level resonance phenomenon, as in our model. However, the resonance phenomenon described here is different from that of Akam et al., since they suggested a feed-forward circuit for band-pass filtering and not the recurrent connections suggested in this study. Moreover, recurrent excitation modulates the resonant frequency by tuning the synaptic weight or connectivity ratio, while the feed-forward structure modulates it by varying the conduction delay of inhibitory synapses. It should be noted, however, that the efficacy of synaptic connections needs to be rapidly adjusted for the dynamic control of information flow. For instance, the coherence between neuronal oscillations of various subregions of the hippocampus varies rapidly during exploratory behavior and spatial tasks37,38,39. Such a rapid change of synaptic efficacy can be achieved by the regulation of neuromodulatory substances. For example, the neurotransmitter acetylcholine modulates hippocampal circuitry, giving rise to an abrupt and stable transition between different patterns of oscillations40. Our model seems more biologically plausible than the feed-forward model, since changing the synaptic weight is presumably easier than changing the conduction delay. This also implies that our model might have a potential advantage for dynamic neuronal communication compared to the feed-forward routing mechanism.

Most brain functions require the flexible routing of signals throughout the brain. In other words, a neuronal group needs to flexibly switch among its communication targets in response to demands, such as cognitive or behavioral tasks. A recent study has shown frequency-dependent switching between subregions in the entorhinal cortex (EC) – hippocampal network41. The hippocampal area CA1 can synchronize with area CA3, a hippocampal subregion for the storage of spatial memory, at relatively low gamma frequencies (25–50 Hz), or with the medial entorhinal cortex, an area that provides information about spatial position, at relatively high gamma frequencies (65–140 Hz). A question still remains as to what triggers this frequency-dependent switching. The CA1 circuit is composed of excitatory pyramidal neurons and several other classes of inhibitory interneurons, such as basket cells, bistratified cells, oriens-lacunosum-moleculare cells, and axo-axonic cells. Interestingly, those distinct types of interneurons are recurrently connected with pyramidal cells and contribute differently to the temporal coordination of pyramidal cells during spindle, theta, and gamma oscillations42. We infer that this heterogeneity in cell types may permit the CA1 network to flexibly tune its resonant frequency from the theta- to the gamma- band by combining different types of recurrent connections. As a result, this tuning capability could enable the CA1 region to switch between synchronizing with CA3 and with EC in a frequency-dependent manner. Although a detailed analysis of all of the possible combinations of different types of recurrent connections is not within the scope of this study, the proposed mechanism can be used as a vehicle for understanding frequency-dependent selective communication.

Finally, the mechanism described here can provide important insights into cross-frequency coupling (CFC), a regulatory mechanism between low- and high-frequency brain oscillations43. Recent studies have suggested that CFC might serve as a mechanism for transferring information from a large-scale brain network to a local cortical processing network44,45. Robust coupling between low- and high-frequency bands requires multiple resonant frequencies in a single neuronal group. If we associate local feedback loops in our model with long-range feedback loops between distant brain subregions, such as thalamocortical or corticocortical connections, we can explain the coexistence of low- and high-frequency resonance in a local group, thereby elucidating the mechanism of information transfer from a large-scale to a local brain network. In addition, the CFC has been considered as a putative mechanism involved in cognitive dysfunctions46,47,48. Thus, the mechanism proposed in this study can provide a useful basis for understanding how a CFC disturbance contributes to cognitive dysfunctions.

Different brain rhythms are thought to be associated with different functions of the brain. Gamma frequency rhythms in the cortex are considered to regulate the responses to visual stimuli and convey information about the visual scene49,50,51,52,53. Theta oscillations in the hippocampus are known to carry information about the position and heading in space of the animal54,55. Therefore, the neuronal circuits of the brain should have a wide range of resonant frequencies to capture all the necessary information from a broad band input stimuli. Although our simulation results were limited to the beta band resonant frequency, this study can be extended to lower or higher band frequencies by considering the relevant parameter values for the threshold voltage of excitatory and inhibitory neurons, membrane time constant, refractory time constant, synaptic time delay, etc (see Fig. S5 as an example of mutual information analysis for the broad band resonant frequency).

Methods

Neuron model

All neurons were described by the spike response model26. The membrane potential of neuron i at time t obeys the following equation:

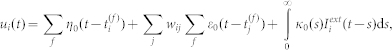graphic file with name srep02519-m14.jpg

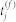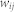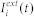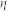where Inline graphic is the firing time of a presynaptic neuron j, Inline graphic is the synaptic efficacy from a presynaptic neuron j to a postsynaptic neuron i, and Inline graphic denotes the external input current to neuron i. The postsynaptic potentials are influenced by inputs from adjacent neurons (Inline graphic-kernel), as well as the external input current (Inline graphic-kernel), and accumulate until the firing threshold is reached. In the simulations performed, a constant threshold was assumed. After firing an output spike, the postsynaptic potential is reset to a value below the resting potential, which is referred to as a hyperpolarizing spike after-potential (Inline graphic-kernel). Response kernels are described by:

graphic file with name srep02519-m21.jpg
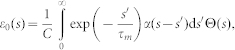graphic file with name srep02519-m22.jpg
graphic file with name srep02519-m23.jpg

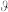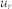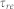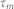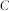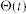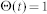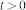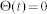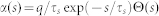where Inline graphic, Inline graphic, Inline graphic, Inline graphic, and Inline graphic denote the firing threshold, resting potential, refractory time constant, membrane time constant, and capacitance, respectively. Inline graphic is the Heaviside step function with Inline graphic for Inline graphic and Inline graphic otherwise. As the postsynaptic current should have a finite duration, Inline graphic-function was adopted for the postsynaptic current Inline graphic with electric charge 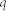Inline graphic and time constant 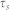Inline graphic. 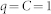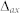With Inline graphic, Inline graphic-kernel becomes:

graphic file with name srep02519-m39.jpg

where Inline graphic is the axonal transmission delay. All neurons were assumed to have an identical parameter set 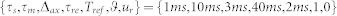Inline graphic, where 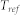Inline graphic is the absolute refractory time. Using this parameter set, the gain function of a neuron was determined, and the corresponding feasible input range was estimated by extensive simulations (see Supplementary Notes and Fig. S1(a)).

Network architecture

A neural network composed of 8,000 excitatory principal neurons and 2,000 inhibitory interneurons was considered. The network response of a neuronal group is limited to the collective behavior of only excitatory neurons, since pyramidal neurons mostly contribute to the generation of local field potentials (LFPs) in cortex and the hippocampus56. Synchronized oscillations are generated by complex interactions between neurons rather than a simple summation of individual firings. This study focused only on the network-based oscillation patterns that are primarily determined by network structure parameters: connectivity ratio R, synaptic weight W, and conduction delay d. In a negative feedback structure (Fig. 1(a)), all excitatory (inhibitory) neurons are randomly connected with inhibitory (excitatory) neurons with a connection probability of Rie (Rei) and a synaptic efficacy of Wie (Wei). For simplicity, Rie = Rei = R and 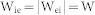Inline graphic were set for all simulations. For mutual excitation and inhibition (Fig. 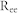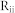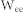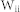2(a)), Inline graphic and Inline graphic were used for the corresponding connectivity ratios, and Inline graphic and Inline graphic for the corresponding synaptic weights. A total of 10,000 cells were used, as this is the most suitable network size for a realizable computation time. Previous studies have shown that the activity of a network becomes independent of the network size beyond about 10,000 neurons57,58. Twenty trials of each simulation were carried out. To investigate selective communication between groups (Fig. 3(c)), three groups were considered, each composed of 2,000 excitatory and 500 inhibitory neurons. The values of R and W were set to 0.1, so that the resonant frequency would be equivalent to that of the previous network (N = 10,000), in which R = W = 0.05. The total output from a neuron is determined by the product of the total number of outgoing synapses 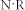Inline graphic and synaptic weight W, i.e., 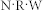Inline graphic. If the value of 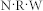Inline graphic is conserved, e.g., Inline graphic, then the resonant frequency should also be preserved.

External inputs

Three types of input signals were used, including uniform white noise, sinusoidally oscillating input, and constant input with Gaussian white noise. In all simulations, it was assumed that both excitatory and inhibitory neurons receive external inputs. To find the resonant frequency of NF, ME, and MI network structures, uniform white noise ranging from 0 to 0.8 (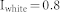Inline graphic) was used and a resonant frequency was found that is not influenced by any small perturbation of input strength (Fig. 1(c)). To investigate the response of each structure to oscillating inputs, the strength of the uniform white noise and the oscillation amplitude was varied between 0.16 and 1.0, and the simulation was repeated over 100 combinatory inputs (Fig. 3(b)). In the last part of the Results section (Fig. 3(c)), the case was considered in which two sender groups receive both external input and background noise input while a receiver group receives only background noise input, except for signals from excitatory neurons in the sender groups. Hence, a constant input 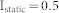Inline graphic was used with a random Gaussian variation (SD = 0.05) for sender groups and uniform white noise input 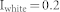Inline graphic for the receiver group.

Synchronization index

To measure the degree of synchrony of a neuronal population, a synchronization index (SI) based on the autocorrelogram was used30. All spikes from excitatory neurons in a group were compiled in 1 ms bins, which resulted in a spike-time histogram, as shown in Supplementary Fig. S2(a). As this histogram is highly autocorrelated, the autocorrelation function (AC) follows a cosine pattern, giving rise to a maximal inner product of AC and cosine function with a period of 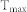Inline graphic. After normalization, the SI becomes:

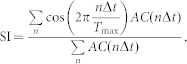graphic file with 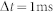name srep02519-m56.jpg

with Inline graphic. An SI value of unity occurs when neurons fire at time intervals that are multiples of a period T and zero when neurons fire incoherently. This index measures the rhythmicity of the synchronized oscillation. However, if every spike occurs exactly at the same time with the same period, it results in the perfect synchronization with SI = 1, irrespective of how many neurons fire. Thus, the SI was modified for population synchrony by multiplying the ratio of the average instantaneous firing rate (computed in 1 ms bins) and the maximum firing rate of excitatory neurons,

graphic file with name srep02519-m58.jpg

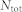where Inline graphic is the total number of neurons and A is the amplitude of synchronized oscillations. Perfect synchronization occurs when all excitatory neurons fire at the same periodic time, and low synchronization when either few neurons fire or neurons fire incoherently.

Author Contributions

K.-H.C. designed the project and supervised the research; D.S. and K.-H.C. performed the mathematical modeling and analysis; and D.S. and K.-H.C. wrote the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep02519-s1.pdf (1.2MB, pdf)

Acknowledgments

This work was supported by the National Research Foundation of Korea (NRF) grants funded by the Korea Government, the Ministry of Science, ICT & Future Planning (2009-0086964, 2010-0017662, and 2013046303). This work was also supported by GIST Systems Biology Infrastructure Establishment Grant (2013) and by the KUSTAR-KAIST Institute, Korea, under the R&D program supervised by the KAIST.

References

  1. Dosenbach N. U. F. et al. Distinct brain networks for adaptive and stable task control in humans. Proc Natl Acad Sci USA 104, 11073–11078 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Engel A. K., Fries P. & Singer W. Dynamic predictions: oscillations and synchrony in top-down processing. Nat Rev Neurosci 2, 704–716 (2001). [DOI] [PubMed] [Google Scholar]
  3. Fries P. A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends in Cognitive Sciences 9, 474–480 (2005). [DOI] [PubMed] [Google Scholar]
  4. Hipp J. F., Engel A. K. & Siegel M. Oscillatory synchronization in large-scale cortical networks predicts perception. Neuron 69, 387–396 (2011). [DOI] [PubMed] [Google Scholar]
  5. Salinas E. & Sejnowski T. J. Correlated neuronal activity and the flow of neural information. Nat Rev Neurosci 2, 539–550 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Varela F., Lachaux J. P., Rodriguez E. & Martinerie J. The brainweb: phase synchronization and large-scale integration. Nat Rev Neurosci 2, 229–239 (2001). [DOI] [PubMed] [Google Scholar]
  7. Gregoriou G. G., Gotts S. J., Zhou H. & Desimone R. High-Frequency, Long-Range Coupling Between Prefrontal and Visual Cortex During Attention. Science 324, 1207–1210 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Saalmann Y. B., Pigarev I. N. & Vidyasagar T. R. Neural mechanisms of visual attention: how top-down feedback highlights relevant locations. Science 316, 1612–1615 (2007). [DOI] [PubMed] [Google Scholar]
  9. Siegel M., Donner T. H., Oostenveld R., Fries P. & Engel A. K. Neuronal synchronization along the dorsal visual pathway reflects the focus of spatial attention. Neuron 60, 709–719 (2008). [DOI] [PubMed] [Google Scholar]
  10. Palva J. M., Monto S., Kulashekhar S. & Palva S. Neuronal synchrony reveals working memory networks and predicts individual memory capacity. Proc Natl Acad Sci U S A 107, 7580–7585 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Singer W. Neuronal synchrony: a versatile code for the definition of relations? Neuron 24, 49–65, 111–125 (1999). [DOI] [PubMed] [Google Scholar]
  12. Singer W. & Gray C. M. Visual feature integration and the temporal correlation hypothesis. Annu Rev Neurosci 18, 555–586 (1995). [DOI] [PubMed] [Google Scholar]
  13. von der Malsburg C. & Schneider W. A neural cocktail-party processor. Biol Cybern 54, 29–40 (1986). [DOI] [PubMed] [Google Scholar]
  14. Engel A. K., Roelfsema P. R., Fries P., Brecht M. & Singer W. Role of the temporal domain for response selection and perceptual binding. Cereb Cortex 7, 571–582 (1997). [DOI] [PubMed] [Google Scholar]
  15. Roelfsema P. R., Engel A. K., Konig P. & Singer W. Visuomotor integration is associated with zero time-lag synchronization among cortical areas. Nature 385, 157–161 (1997). [DOI] [PubMed] [Google Scholar]
  16. Schoffelen J.-M., Oostenveld R. & Fries P. Neuronal coherence as a mechanism of effective corticospinal interaction. Science 308, 111–113 (2005). [DOI] [PubMed] [Google Scholar]
  17. Womelsdorf T. et al. Modulation of neuronal interactions through neuronal synchronization. Science 316, 1609–1612 (2007). [DOI] [PubMed] [Google Scholar]
  18. Buzsáki G. Rhythms of the brain. 61–79 (Oxford University Press, 2006). [Google Scholar]
  19. Börgers C. & Kopell N. Synchronization in networks of excitatory and inhibitory neurons with sparse, random connectivity. Neural computation 15, 509–538 (2003). [DOI] [PubMed] [Google Scholar]
  20. Brunel N. & Hakim V. Fast global oscillations in networks of integrate-and-fire neurons with low firing rates. Neural computation 11, 1621–1671 (1999). [DOI] [PubMed] [Google Scholar]
  21. Morita K., Kalra R., Aihara K. & Robinson H. P. Recurrent synaptic input and the timing of gamma-frequency-modulated firing of pyramidal cells during neocortical "UP" states. J Neurosci 28, 1871–1881 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Whittington M. A., Traub R. D., Kopell N., Ermentrout B. & Buhl E. H. Inhibition-based rhythms: experimental and mathematical observations on network dynamics. Int J Psychophysiol 38, 315–336 (2000). [DOI] [PubMed] [Google Scholar]
  23. D'angelo E. et al. Timing in the cerebellum: oscillations and resonance in the granular layer. Neuroscience 162, 805–815 (2009). [DOI] [PubMed] [Google Scholar]
  24. Gray C. M. & Singer W. Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc Natl Acad Sci USA 86, 1698–1702 (1989). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Marshall S. P. & Lang E. J. Inferior olive oscillations gate transmission of motor cortical activity to the cerebellum. Journal of Neuroscience 24, 11356–11367 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Gerstner W. & M. Kistler W. Spiking neuron models: single neurons, populations, plasticity. 93–145 (Cambridge University Press, 2002). [Google Scholar]
  27. Horowitz J. M. Evoked activity of single units and neural populations in the hippocampus of the cat. Electroencephalogr Clin Neurophysiol 32, 227–240 (1972). [DOI] [PubMed] [Google Scholar]
  28. Leung L. S. & Yu H. W. Theta-frequency resonance in hippocampal CA1 neurons in vitro demonstrated by sinusoidal current injection. J Neurophysiol 79, 1592–1596 (1998). [DOI] [PubMed] [Google Scholar]
  29. Wilson H. R. & Cowan J. D. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J 12, 1–24 (1972). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Maex R. & De Schutter E. Synchronization of golgi and granule cell firing in a detailed network model of the cerebellar granule cell layer. J Neurophysiol 80, 2521–2537 (1998). [DOI] [PubMed] [Google Scholar]
  31. Tsai T. Y. et al. Robust, tunable biological oscillations from interlinked positive and negative feedback loops. Science 321, 126–129 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Kim J. R., Shin D., Jung S. H., Heslop-Harrison P. & Cho K. H. A design principle underlying the synchronization of oscillations in cellular systems. J Cell Sci 123, 537–543 (2010). [DOI] [PubMed] [Google Scholar]
  33. de Carvalho J. X. & Prado C. P. C. Self-organized criticality in the Olami-Feder-Christensen model. Phys Rev Lett 84, 4006–4009 (2000). [DOI] [PubMed] [Google Scholar]
  34. Zapperi S., Lauritsen K. B. & Stanley H. E. Self-organized branching processes: mean-field theory for avalanches. Phys Rev Lett 75, 4071–4074 (1995). [DOI] [PubMed] [Google Scholar]
  35. Vogels T. P. & Abbott L. F. Gating multiple signals through detailed balance of excitation and inhibition in spiking networks. Nat Neurosci 12, 483–491 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Akam T. & Kullmann D. M. Oscillations and filtering networks support flexible routing of information. Neuron 67, 308–320 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Bragin A. et al. Gamma (40–100 Hz) oscillation in the hippocampus of the behaving rat. J Neurosci 15, 47–60 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Chrobak J. J. & Buzsaki G. Gamma oscillations in the entorhinal cortex of the freely behaving rat. J Neurosci 18, 388–398 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Montgomery S. M. & Buzsaki G. Gamma oscillations dynamically couple hippocampal CA3 and CA1 regions during memory task performance. Proc Natl Acad Sci U S A 104, 14495–14500 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Fellous J. M. & Sejnowski T. J. Cholinergic induction of oscillations in the hippocampal slice in the slow (0.5–2 Hz), theta (5–12 Hz), and gamma (35–70 Hz) bands. Hippocampus 10, 187–197 (2000). [DOI] [PubMed] [Google Scholar]
  41. Colgin L. L. et al. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature 462, 353–357 (2009). [DOI] [PubMed] [Google Scholar]
  42. Klausberger T. & Somogyi P. Neuronal diversity and temporal dynamics: the unity of hippocampal circuit operations. Science 321, 53–57 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Canolty R. T. et al. High gamma power is phase-locked to theta oscillations in human neocortex. Science 313, 1626–1628 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Canolty R. T. & Knight R. T. The functional role of cross-frequency coupling. Trends in Cognitive Sciences 14, 506–515 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Jensen O. & Colgin L. L. Cross-frequency coupling between neuronal oscillations. Trends in Cognitive Sciences 11, 267–269 (2007). [DOI] [PubMed] [Google Scholar]
  46. Lisman J. & Buzsaki G. A neural coding scheme formed by the combined function of gamma and theta oscillations. Schizophr Bull 34, 974–980 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Tort A. B. et al. Dynamic cross-frequency couplings of local field potential oscillations in rat striatum and hippocampus during performance of a T-maze task. Proc Natl Acad Sci U S A 105, 20517–20522 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Axmacher N. et al. Cross-frequency coupling supports multi-item working memory in the human hippocampus. Proc Natl Acad Sci U S A 107, 3228–3233 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Neuenschwander S. & Singer W. Long-range synchronization of oscillatory light responses in the cat retina and lateral geniculate nucleus. Nature 379, 728–732 (1996). [DOI] [PubMed] [Google Scholar]
  50. Laufer M. & Verzeano M. Periodic activity in the visual system of the cat. Vision Res 7, 215–229 (1967). [DOI] [PubMed] [Google Scholar]
  51. Hughes S. W. et al. Synchronized oscillations at alpha and theta frequencies in the lateral geniculate nucleus. Neuron 42, 253–268 (2004). [DOI] [PubMed] [Google Scholar]
  52. Koepsell K. et al. Retinal oscillations carry visual information to cortex. Front Syst Neurosci 3, 4 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Koepsell K. & Sommer F. T. Information transmission in oscillatory neural activity. Biol Cybern 99, 403–416 (2008). [DOI] [PubMed] [Google Scholar]
  54. Huxter J. R., Senior T. J., Allen K. & Csicsvari J. Theta phase-specific codes for two-dimensional position, trajectory and heading in the hippocampus. Nat Neurosci 11, 587–594 (2008). [DOI] [PubMed] [Google Scholar]
  55. O'Keefe J. & Recce M. L. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus 3, 317–330 (1993). [DOI] [PubMed] [Google Scholar]
  56. Mazzoni A., Panzeri S., Logothetis N. K. & Brunel N. Encoding of naturalistic stimuli by local field potential spectra in networks of excitatory and inhibitory neurons. PLoS Comput Biol 4, e1000239 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Diesmann M., Gewaltig M. O. & Aertsen A. Stable propagation of synchronous spiking in cortical neural networks. Nature 402, 529–533 (1999). [DOI] [PubMed] [Google Scholar]
  58. Kumar A., Rotter S. & Aertsen A. Conditions for propagating synchronous spiking and asynchronous firing rates in a cortical network model. J Neurosci 28, 5268–5280 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep02519-s1.pdf (1.2MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES