Table 1.
Typical synaptic kernels in mathematical and graphical form.
| Kernel type | Mathematical expression for filter response | Typical function (Spike at t = 0) |
|---|---|---|
| Stable recurrent connection (leaky integration) with non-linear leak | 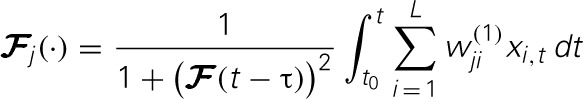 |
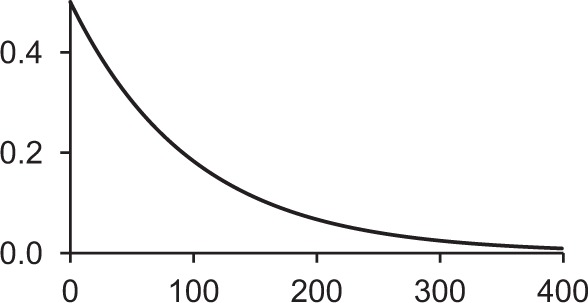 |
| Alpha function followed by compressive non-linearity | 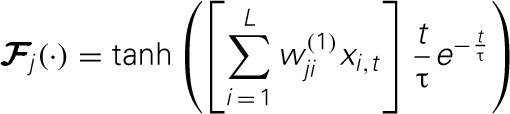 |
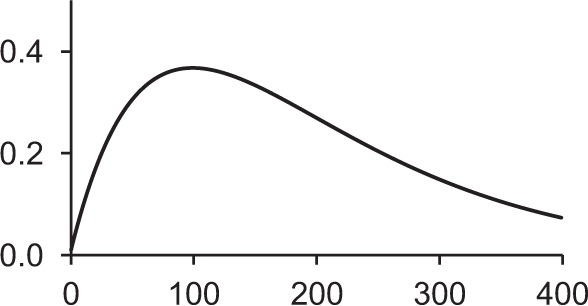 |
| Damped resonant synapse followed by compressive non-linearity | 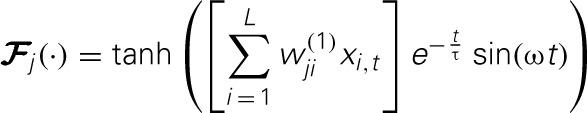 |
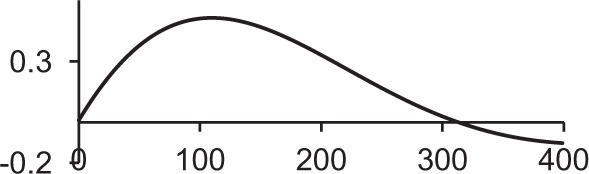 |
| Synaptic or dendritic delay with alpha function, followed by compressive non-linearity |
for t ≥ △T:
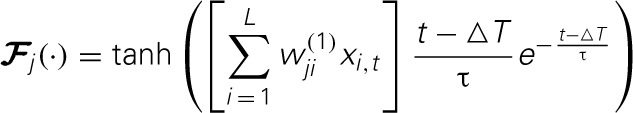
|
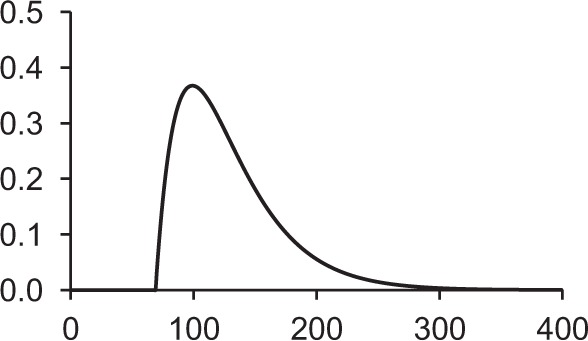 |
|
for t < △T:
| ||
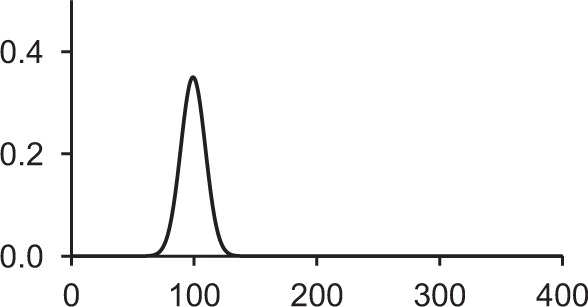
| Synaptic or dendritic delay with Gaussian function, followed by compressive non-linearity |
for t ≥ △T: 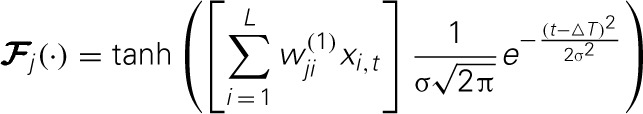
|
 |
|
for t < △T:
|
The order from top to bottom provides increasingly precise delay timing; with the exception of the leaky integrator, time constants were chosen for maximum synaptic transmission at 100 timesteps after spiking. Variables are as for Equation 1. τ is the time constant for the various functions, ΔT is an explicit synaptic or dendritic delay, and ω the natural resonant frequency for a damped resonant synaptic function. The horizontal axes indicate timesteps.
