|
|
| Algorithm 1 Distributed matrix completion algorithm for recognition, on the ith processing node. |
|
|
| Input: Initial portion of the data matrix for the ith node, Di = D0i, and parameter, λ. |
| Output: ith portion of the completed matrix, Di |
| ℒi0, = 0, μk > 0, ρ = 1.1, Ei0 = 0 |
| while not converged do |
| 1. Fix all other variables and update |
| by: |
| ci(k) = JikT Jik |
Send ci(k) to all the neighbors,
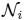 , , |
Receive all cj(k)s from the neighbors,
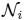 , , |
ci(k) = ci(k) +
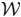 (k) Σj∈ (k) Σj∈
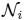 (cj(k) − ci(k)) (cj(k) − ci(k)) |
| (V, , VT) = svd(ci(k)) |
| Ui = Jik VΣ−1 |
Dik+1= Ui
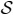 τ[Σ] VT τ[Σ] VT
|
| 2. Fix all other variables and update |
| 3. Fix all other variables and update |
| 4. Set the , |
| 5. Update the multiplier, ℒi: ℒik+1 = ℒik + μk(Dik+1 − Di0 − Eik+1) |
| 7. Update parameter, μk+1, as: μk+1= min(ρμk, 1010) and k = k + 1. |
| 8. Check the convergence condition: (Dik − D0i −Eik → 0) |
| end while |
|
|

An official website of the United States government
Here's how you know
Official websites use .gov
A
.gov website belongs to an official
government organization in the United States.
Secure .gov websites use HTTPS
A lock (
) or https:// means you've safely
connected to the .gov website. Share sensitive
information only on official, secure websites.