A mathematical evaluation of hemodynamic parameters after carotid eversion and conventional patch angioplasty

Abstract

Carotid endarterectomy has a long history in stroke prevention, yet controversy remains concerning optimal techniques. Two methods frequently used are endarterectomy with patch angioplasty (CEAP) and eversion endarterectomy (CEE). The objective of this study was to compare hemodynamics-related stress and strain distributions between arteries repaired using CEAP and CEE. Mathematical models were based on in vivo three-dimensional arterial geometry, pulsatile velocity profiles, and intraluminal pressure inputs obtained from 16 patients with carotid artery disease. These data were combined with experimentally derived nonlinear, anisotropic carotid artery mechanical properties to create fluid-structure interaction models of CEAP and CEE. These models were then used to calculate hemodynamic parameters thought to promote recurrent disease and restenosis. Combining calculations of stress and strain into a composite risk index, called the integral abnormality factor, allowed for an overall comparison between CEAP and CEE. CEE demonstrated lower mechanical stresses in the arterial wall, whereas CEAP straightened the artery and caused high stress and strain concentrations at the suture-artery interface. CEAP produced a larger continuous region of oscillatory, low-shear, vortical flow in the carotid bulb. There was a more than two-fold difference in the integral abnormality factor, favoring CEE. In conclusion, in a realistically simulated carotid artery, fluid-structure interaction modeling demonstrated CEE to produce less mechanical wall stress and improved flow patterns compared with CEAP. Clinical validation with larger numbers of individual patients will ultimately be required to support modeling approaches to help predict arterial disease progression and comparative effectiveness of reconstruction methods and devices.

carotid artery reconstruction for stroke prevention was first described in 1954, and, since then, carotid endarterectomy (CEA) has become a frequently performed operation for patients with cerebrovascular disease (5). Over this time period, multiple techniques have been developed to accomplish the goals of atherosclerotic plaque removal and subsequent arterial reconstruction. These techniques have converged primarily to two methods: conventional CEA and carotid eversion endarterectomy (CEE). Conventional CEA involves a longitudinal arteriotomy at the carotid bifurcation, removal of the atherosclerotic plaque, and closure of the arteriotomy either primarily or, more often, with a patch (CEAP). CEE involves oblique transection of the internal carotid artery (ICA) at its origin, rolling the artery back on itself to remove the plaque, and then reimplantation of the ICA back onto its original location.

Multiple trials have been conducted comparing arterial reconstruction techniques during CEA. Level one clinical evidence showing inferiority of primary closure versus CEAP has been widely published (1, 8, 49). A number of studies comparing CEAP with CEE have also been published (2, 3, 11, 63); however, the evidence is not clear cut, and controversy still remains within the clinical data on which of the two methods is superior. Although some patients would likely benefit from one approach or the other based on certain factors, such as anatomic and lesion characteristics, it is unknown which one might produce optimal hemodynamics and mechanics within the average postoperative carotid artery. This is particularly important because arterial disease is currently thought to be strongly influenced by adverse cellular responses to specific hemodynamic environments, such as low and oscillatory shear blood flow patterns and high mechanical wall stress and strain concentrations (12, 15, 20, 51).

Mechanical and flow characteristics linked to recurrent disease development can be studied with engineering and computational methods. In recent years, mathematical modeling of arteries has matured immensely with the emergence of better three-dimensional (3-D) imaging, mesh generation, and visualization technologies, largely thanks to tremendous advances in computation. Using mathematical modeling, one can now accurately calculate blood flow and arterial wall phenomena following simulations of each of the two carotid repair techniques and perform their objective comparison. Our hypothesis was that mathematical modeling would demonstrate significantly improved hemodynamic and mechanical characteristics favoring CEE compared with CEAP.

METHODS

Informed consent was obtained from 16 consecutive male patients with severe carotid artery atherosclerotic disease [>80% stenosis by North American Symptomatic Carotid Endarterectomy Trial criteria (19)] undergoing CEA. Each patient underwent preoperative computerized tomographic angiography (CTA) of the neck and intraoperative duplex ultrasound of the surgically exposed carotid artery with simultaneous intraluminal pressure measurement.

Mean carotid artery geometry.

Preoperative CTA DICOM data were obtained with a 64-channel scanner Brilliance 64 (Philips, Cleveland, OH). For each patient, two-dimensional cross-sectional images of 100-mm carotid artery segments (Fig. 1) were acquired with an axial step of 1 mm. After individual segmentations, mean features of the arterial geometry were extracted (32), and cross-sections were connected together using Solid Works computer-aided design software (Dassault Systemes, Concord, MA) to form a 3-D solid body of the mean carotid artery.

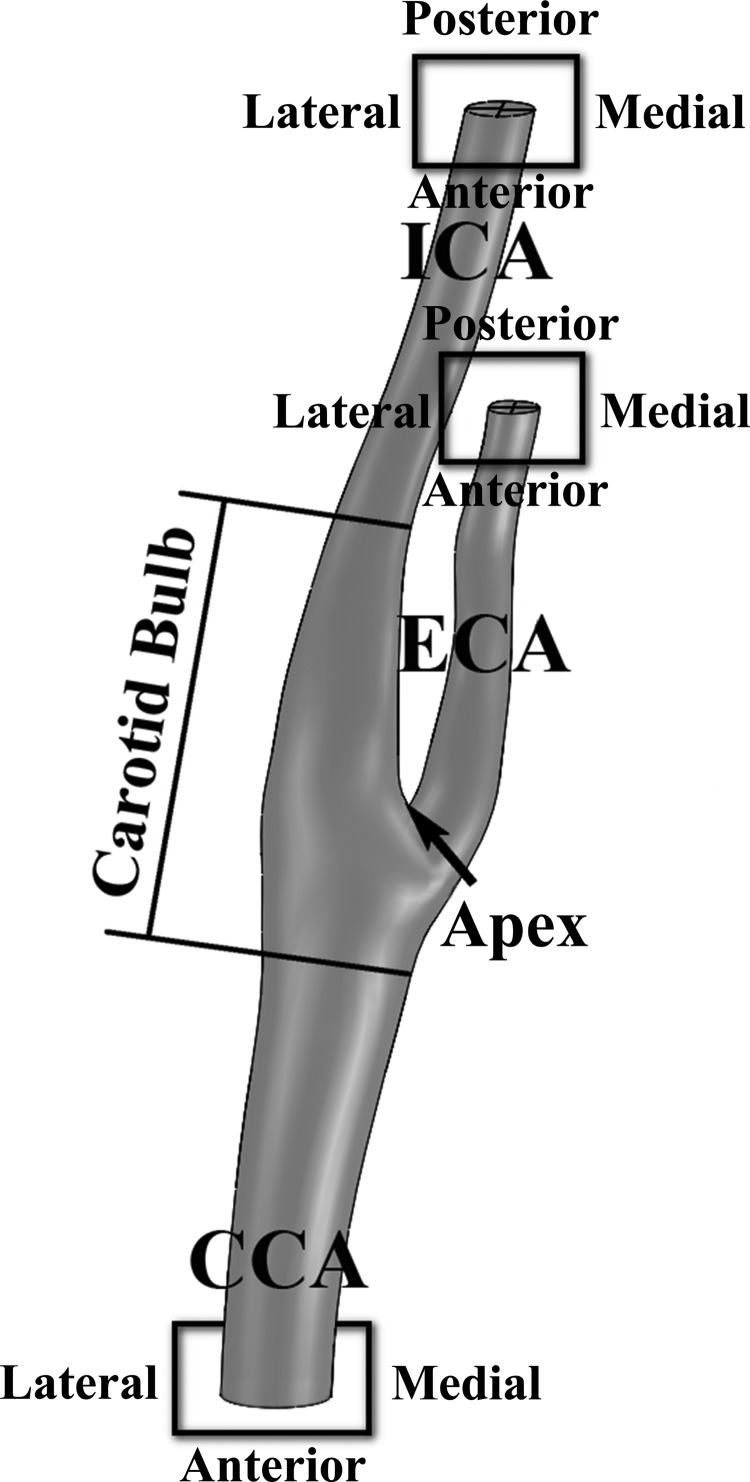
Fig. 1.

Scheme of the carotid artery bifurcation showing the carotid bulb, apex, and conventions on orientations (anterior-posterior and lateral-medial) for the common carotid artery (CCA), internal carotid artery (ICA), and external carotid artery (ECA).

Patient-specific 3-D arterial geometry contains individual features that have profound effects on hemodynamics. Although various geometric characteristics of the human carotid artery have previously been reported by multiple groups (18, 41, 66), in this study we used our own geometric data (32) because they are used in combination with the flow characteristics measured in the same patient group (30), which is crucial for the accurate characterization of fluid and solid interaction hemodynamics (18, 41, 66).

The built mean arterial geometry was then modified to simulate CEAP [with polytetrafluorethylene (PTFE)] and CEE. Many types of patches are currently available, and previous work (33) has modeled hemodynamic results using different patch materials, sizes, and arteriotomy locations in the repaired carotid artery. For this study, we chose PTFE as it is one of the most commonly used prosthetic patching materials for carotid artery repair (45). Arterial wall thickness of the endarterectomized region was made half of that of the normal wall to account for the removal of intima and part of media during CEA (34). Each suture bite accounted for 0.5 mm of material removal from both sides of each arteriotomy in the circumferential direction.

Data on carotid geometry from a group of healthy patients were not available, and control (i.e., unoperated with no stenosis) geometry was not considered. Use of preoperative CTA data and performance of “virtual endarterectomy” was favored versus the use of postoperative CTA scans for two reasons. First, geometry obtained from preoperative scans was independent of the type of actual surgical closure used. Second, the geometry was free of any technical defects such as an endarterectomy produced CCA step or lumen tapering, i.e., it represented the “best-case scenario” for both CEAP and CEE.

Inlet/outlet velocity profiles and pressure.

Pulsatile velocity profiles (temporal and spatial variations of velocity) were measured intraoperatively in the ICA and external carotid artery (ECA) using Duplex ultrasound (Pro Focus 2202, probe 8809, B-K Medical, Herlev, Denmark) (30). Concurrently, the pulsatile pressure waveform (temporal variation of pressure) was measured in the proximal common carotid artery (CCA) using a 21-gauge angiocatheter (31). Although both the velocity and pressure profiles in the carotid artery have been relatively well studied by other groups (4, 17, 47), our measurements were performed in the same group of patients used to build the arterial geometry. Knowledge of correlated blood velocity and pressure waveforms in the distal ICA, ECA, and proximal CCA is required to realistically simulate the blood flow through the entire carotid bifurcation.

Mathematical model.

The simulations used a finite-element method (ADINA R&D, Watertown, MA) with unstructured meshes used for both the fluid (blood flow) and solid (arterial wall) domains constructed using the Octree method (6). Dependence of the results on the size of the finite-element mesh was carefully studied, and the selected mesh size (150,000/115,000 fluid/solid elements) ensured that the error of calculations did not exceed 5%. Use of a heavily validated commercially available solver does not guarantee the correctness of model formulation, but it does avoid algorithm implementation errors, ensures repeatability of the results, and increases their translational value.

Continuity and the full Navier-Stokes equations in arbitrary Lagrangian-Eulerian formulation (to account for the moving fluid-structure interface) were solved for the fluid. Blood was modeled as non-Newtonian fluid as described by the Carreau constitutive law, which accurately describes the shear thinning rheological behavior of blood in arteries (29). The momentum conservation equation in Lagrangian description for large displacements and large strains was solved for the solid domain.

Although in reality the arterial wall consists of three layers (the intima, media, and adventitia), each with its own unique properties, here it was modeled as a single-layered nonlinear hyperelastic anisotropic material with strain energy proposed by Holzapfel et al. (23). Recently, biaxial mechanical properties of the carotid wall layers have been measured by Sommer et al. (55). However, clinical CTA data (used to build the 3-D geometry) do not yet have sufficient resolution to allow the identification of separate layers; therefore, the wall was treated as bulk material. For consistency with our previous study (33) investigating the hemodynamic effects of different carotid patch materials, we have determined the constitutive parameters for the carotid wall and patch from our own biaxial tests (35). We note that even though in vivo measurements of carotid mechanical properties are available from both our (31) and other groups (9, 42, 57), they were not used because they were not sufficient to characterize the nonlinear anisotropic behavior of the tissue. Circumferential residual stress was not included in the analysis because we speculate that most of it is released by arteriotomy. Axial residual stress was not included because arteries lose their ability to retract upon transection in senior patients with vascular disease (24, 53).

To make simulations more realistic, we incorporated the surgical suture into the model. Suture was introduced as rigid links connecting neighboring finite-element nodes on both sides of the arteriotomy, such that distance between these nodes remained constant during pulsation. Since suture is significantly stiffer than the arterial wall, this technique allowed to significantly reduce the computational time required to suffice the refined meshes around the suture entry site (33).

Full coupling between the blood flow and the arterial wall was achieved by imposing the compatibility of displacements, equilibrium of tractions, and no-slip conditions on the fluid-structure interface. This was enforced iteratively between the fluid and solid solvers (each solving a different set of equations for the blood flow and arterial wall, respectively) at each time step until sufficient convergence was reached.

Analysis of mechanical factors related to early and late restenosis.

Early carotid restenosis is usually due to myointimal hyperplasia caused by the mechanical injury of the arterial wall (15, 51, 62). Injury can be induced by high strains and stresses in the wall imposed cyclically by the internal blood pressure. Late restenosis is usually due to atherosclerosis. It is associated with flow phenomena, namely, low and oscillatory [oscillatory shear index (OSI)] wall shear stress (WSS) and long platelet residence time (T_r) (12–14, 20, 43). All these factors were compared between models of carotid arteries repaired with CEE and CEAP.

Strains and stresses acting inside the arterial wall were evaluated by calculating the cyclic strain (CS) and effective stress (ES) [or Von Mises stress (VM)] quantities. CS was computed as the difference between VM strains calculated at peak systole and late diastole as follows:

$${\epsilon }_{\text{VM, cyclic}}={\epsilon }_{\text{VM, peak systole}}-{\epsilon }_{\text{VM, late diastole}}$$ (1)

where the VM strain invariant is defined as follows:

$${\epsilon }_{\text{VM}}={\left[\frac{{\left({\epsilon }_{\text{I}}-{\epsilon }_{\text{II}}\right)}^2+{\left({\epsilon }_{\text{II}}-{\epsilon }_{\text{III}}\right)}^2+{\left({\epsilon }_{\text{I}}-{\epsilon }_{\text{III}}\right)}^2}{2}\right]}^{1/2}$$ (2)

and ε_I, ε_II, and ε_III are the principal Green-Lagrange strains. ES was calculated using Eq. 2 substituting strains for stresses. It follows from Eqs. 1 and 2 that CS quantifies the amount of arterial wall deformation during the cardiac cycle, whereas ES represents the gross stress response of the artery, which is largest during peak systole. We note that ES here is not used to assess the failure of the artery but rather to determine segments of the wall that potentially experience more injury and damage than those at which the ES is low. The choice of ES instead of individual stress components is conditioned by the fact that ES includes the influence of all stress components acting at a given point in the arterial wall.

WSS was evaluated as the temporal mean during the complete cardiac cycle to provide the average hemodynamic effect indicator. Calculation of WSS involved multiplication of the dynamic viscosity with the velocity gradient projected onto the luminal surface and calculated in the direction of local unit surface normal (n̂_s), as follows:

$${\tau }_{\text{s}}=\mu \frac{\partial u}{\partial {n^}_s}$$ (3)

where τ_s is WSS, μ is variable blood viscosity, and ∂u/∂n̂_s is the velocity gradient in the direction of surface normal.

The oscillatory nature of the blood flow was evaluated by calculating OSI, as suggested by Ku et al. (38):

$$\text{OSI}=\frac{1}{2}\left(1-\frac{{\displaystyle {\int }_0^T}{\overline{\mathbf{\tau }}}_{\text{s}}\text{d}t}{{\displaystyle {\int }_0^T}\left|{\overline{\mathbf{\tau }}}_{\text{s}}\right|\text{d}t}\right)$$ (4)

where τ̄_s is the instantaneous WSS vector (|τ̄_s| = τ_s) and T is the length of the cardiac cycle. OSI is a dimensionless measure that quantifies the departure of the WSS vector from its predominant axial alignment. It is important to note that OSI does not take into account the magnitude of WSS and only considers direction.

Dimensionless endothelial T_r was calculated as previously described by Gay and Zhang (22) as follows:

$$T_{\text{r}}=\frac{\mu }{T}{\left[\left(1-2\text{OSI}\right)\langle {\tau }_{\text{s}}\rangle \right]}^{-1}$$ (5)

where <> represents the time-averaged quantity. We note that T_r is evaluated only in the vicinity of the endothelial surface; therefore, it does not consider the convection of platelets to/from the core of the flow.

To address this issue, the concept of flow-field coherent vortical structures (VSs) was implemented in conjunction with the λ₂ vortex-eduction technique (28) to identify flow regions surrounding a local pressure minimum that may trap the platelets inside (14). The lasting time of the VS during the cardiac cycle then provided the information on T_r inside the VS core.

Calculation of the composite risk index: the integral abnormality factor.

The integral abnormality factor (A_F) metric was introduced to assess the combined risk of both early and late carotid restenosis after CEAP and CEE. Early restenosis is thought to be associated with myointimal hyperplasia caused by the mechanical stresses and strains in the wall (15, 51, 62), whereas late restenosis (due to atherosclerosis) is linked to the flow features (12–14, 20, 43). Since most flow features are thought to be related to atherogenesis through WSS, there are essentially only three independent factors: WSS, CS, and ES, each with its own unique distribution. To come up with a single metric for the risk index, we followed the method suggested by Kamenskiy et al. (33) of weighing CS, ES, and WSS according to the domain they belong to. Namely, CS and ES [related to early restenosis through injury (15, 51)] were weighted as 0.25 each, whereas WSS [related to late restenosis through atherogenesis (12, 20)] was assigned a weight of 0.5, as follows:

$${\text{A}}_{\text{F}}=\frac{A_{\text{CS}}}{4A_{\text{CS}}^{\text{CEE}}}\times 100\%+\frac{A_{\text{ES}}}{4A_{\text{ES}}^{\text{CEE}}}\times 100\%+\frac{A_{\text{WSS}}}{4A_{\text{WSS}}^{\text{CEE}}}\times 100\%$$ (6)

where A_CS and A_ES are areas of high CS (calculated using Eqs. 1 and 2) and ES (calculated for peak systole), and A_WSS is the area of low temporal mean WSS. Normalization of A_CS, A_ES, and A_WSS to areas calculated for CEE allowed the direct estimation and comparison of CEA efficacies. Thresholds for A_CS, A_ES, and A_WSS were selected as follows: CS, >0.138; ES, >220 kPa (corresponding to >5.34 in log₁₀ ES contours), and WSS, <0.4 Pa (43). Threshold values of CS and ES were chosen based on average CS and ES values observed in both models. We note that weighting CS, ES, and WSS based solely on domain affiliation was purely hypothetical, and additional studies are required to establish the true influence of each factor on the overall risk.

RESULTS

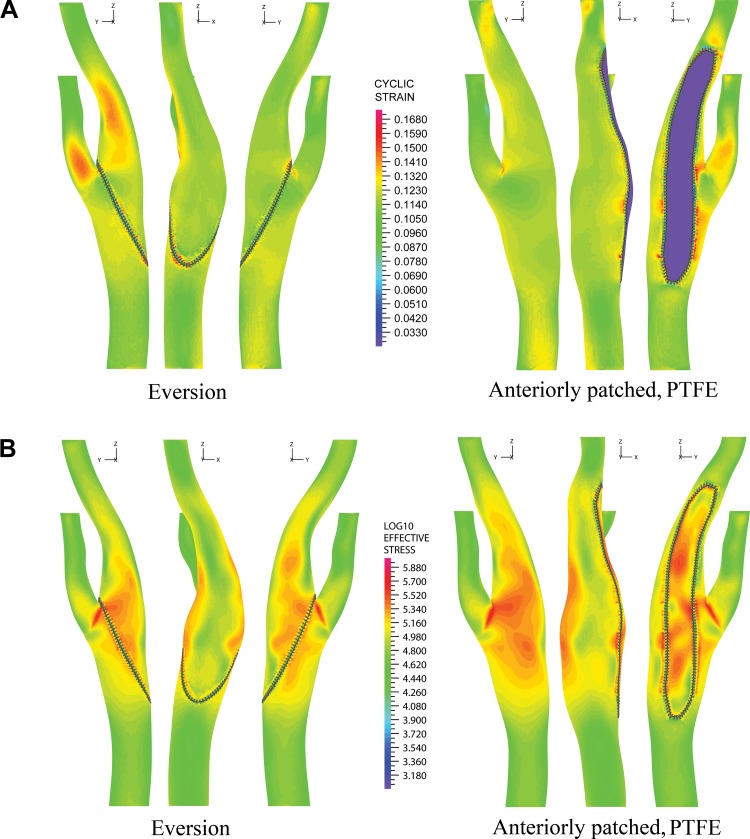
Mathematical models of carotid arteries repaired with CEE and CEAP were compared in terms of hemodynamic factors. Contours of CS for CEE and CEAP are shown in Fig. 2A. A common feature in both models was high CS in the carotid apex, throughout the bulb, and at the ends of suture entry in the arterial wall. In CEE, high CS was also present in the ECA and ICA on the posterior aspect of the artery distal to the extent of the endarterectomy. This was due to straightening of the anterior-posterior bend during systole and its return to the initial curved configuration during diastole. In the case of CEAP, the stiff PTFE patch kept the artery straight during the entire cardiac cycle, which lowered CS in the distal ICA and ECA but resulted in bulging of the more compliant wall around the patch boarders.

Fig. 2.

A and B: cyclic strain (CS) and effective stress (ES) for anterior, lateral, and posterior views of the carotid artery repaired with carotid eversion endarterectomy (CEE) and carotid endarterectomy with patch (CEAP). CS is mapped to the arterial geometry at late diastole, whereas ES is plotted for peak systole. The common logarithm of ES is used to emphasize the differences between high and low values. PTFE, polytetrafluorethylene (patch).

Contours of ES at peak systole are shown in Fig. 2B. Values at peak systole were used as these have the highest chance for damaging the arterial wall. To emphasize the regions of high ES, we plotted log₁₀ ES. Colorband values represent orders of 10, i.e., 3 is 1 kPa, 6 is 1 MPa, and so forth. Similar to CS, features common to both repairs were the high ES in the carotid apex, throughout the carotid bulb, and at the ends of the suture entry in the wall. The mismatch in stiffness between the patch and the host wall caused the posterior aspect of the artery to bulge out, resulting in high ES distributed circumferentially throughout the bulb. Another feature common to both models was the significantly lower ES on the lateral side of the artery than on its anterior or posterior sides.

Temporal mean WSS contours (in Pa) for both CEE and CEAP are shown in Fig. 3A. The arterial wall was removed from Fig. 3A for better visualization of the blood flow. Distributions of WSS clearly showed that CEAP produced a significantly larger zone of low WSS than CEE. In both types of repairs, the area of low WSS was larger on the anterior aspect of the artery than on its posterior side. The observed phenomena were the result of tortuous geometry characterized by a bend in the anterior-posterior plane centered on the carotid bulb. The bend was considerably straightened by patch angioplasty, which reinforced the anterior aspect of the artery but caused the more compliant wall opposite to the patch to bulge out, producing low WSS area posteriorly.

Fig. 3.

A: temporal mean wall shear stress (WSS; in Pa) contours for anterior, lateral, and posterior views of the carotid artery repaired with CEE and CEAP. A logarithmic scale is in use. Low WSS is represented by shades of dark blue. The wall of the artery was removed for better visualization. Results were mapped to the geometry of the artery at late diastole. B: temporal variations of WSS (in Pa) in the center of the carotid bulb (left; ✩) and in the distal ICA (right; ⋆).

Both CEA techniques had a large continuous region of low WSS in the carotid bulb, whereas the distal ICA demonstrated high WSS. Temporal variations of WSS plotted for the center of the carotid bulb and distal ICA (Fig. 3B) showed that WSS in the bulb did not exceed 0.4 Pa during the entire cardiac cycle. This result was consistent for both CEE and CEAP. WSS lower than 0.4 Pa is believed to stimulate the atherogenic phenotype, whereas values higher than 1.5 Pa are thought to be atheroprotective (43).

OSI contours for both models are shown in Fig. 4A, left. The contours showed that flow was oscillatory in the carotid bulb, with highest oscillations observed in the apex. These areas also exhibited low WSS. OSI was small for CEE but significantly increased for CEAP. Another distinct feature was reduced blood velocity in the bulb, which increases endothelial T_r. Contours of T_r are shown in Fig. 4A, right. Zones on the endothelial surface where platelets spend more time during the cardiac cycle strongly correlated with areas of low WSS and OSI. Shorter T_r was observed in the model with CEE than in the model with CEAP.

Fig. 4.

A: contours of the oscillatory shear index (OSI; left) and endothelial platelet residence time (right) for CEE and CEAP. Results were mapped to the geometry of the artery at late diastole. B: vortical structures at peak systole (left) and late diastole (right) for CEE and CEAP. Vortical structures are colored with scalar shear rate (in s⁻¹).

The core of the flow possessed multiple VSs developed predominantly at sites of relatively high WSS and shear rate, as shown in Fig. 4B. Formation of these vortices was particularly salient during systole and was associated with variations in lumen size along the arterial axis, resulting in a roll up of unstable sheets of spanwise vorticity by Kelvin-Helmholtz instability (7). The carotid artery with CEAP had significantly larger VSs than CEE, with the largest vortex formed on the medial aspect of the bulb. This vortex was present during the first third of the cardiac cycle, after which it was suppressed by the lower flow velocity and shear rate of the diastolic phase. VSs in the proximal CCA and distal ICA and ECA regions with relatively high velocity and shear rate were present during the entire cardiac cycle in both types of CEA.

A_F values for arteries repaired with each surgical technique are shown in Fig. 5. Larger values represent larger areas with abnormal (relative to a defined threshold) hemodynamics, possibly leading to greater risk for recurrent disease. The results shown in Fig. 5 demonstrate that CEE was overall superior to CEAP. Even though the area of high CS was 2-fold larger in CEE than in CEAP, the area of WSS was smaller by 1.5-fold and ES by 5.6-fold. If the patch surface was excluded from calculation of ES (PTFE is biologically inert and can withstand much larger stresses without being damaged), the difference in ES between CEE and CEAP was 1.3-fold, still favoring CEE.

Fig. 5.

Integral abnormality factors (in %) calculated for the carotid artery repaired with CEE and CEAP. Smaller values represent hemodynamically better results.

DISCUSSION

Multiple randomized controlled clinical trials have been conducted comparing CEE with CEAP in terms of perioperative stroke, death rates, and restenosis (2, 3, 11, 16, 36, 39, 63). Results have varied among the trials, and controversy still remains regarding the best method for arterial closure after CEA. With the help of mathematical modeling, we analyzed and compared the hemodynamics of carotid arteries repaired with CEE and with conventional CEAP.

Mathematical modeling of carotid arteries has previously been performed for healthy (44, 67) and severely diseased (40, 58) vessels, in which stenosis is caused primarily by atherosclerosis. Substantial progress has been achieved in making these models maximally realistic (59–61) by including the fluid-structure interaction (47, 67), realistic flow (46, 48, 64, 65), complex effects of geometry (37, 41, 56, 66), and mechanical properties (21, 54). Endarterectomized carotid arteries, however, have received much less attention. In these arteries, early restenosis is frequently due to myointimal hyperplasia, and atheroma mostly appears at later stages.

The first mathematical models of endarterectomized carotids were built by Hyun et al. (26, 27). They assumed rigid walls and were solely focused on the analysis of flow phenomena based on WSS and particle deposition measures, i.e., the long-term atherosclerotic restenosis potential. Up until now, these were the only mathematical models of endarterectomized carotids except for our own recent work (33, 34) that account for the fluid-structure interaction with a nonlinear anisotropic response (35), in vivo determined flow patterns (30), and 3-D geometry (32)–all obtained from the same group of patents with carotid artery disease. To our knowledge, this currently is the most realistic mathematical model of the endarterectomized human carotid artery available. In the present study, we used this model to compare two specific endarterectomy procedures, CEE and CEAP, to determine the technique that results in better postoperative hemodynamics in terms of factors that likely influence both early and late restenosis.

Our in silico analysis using the mean carotid artery showed that CEE may offer potential hemodynamic benefits over CEAP for the “average” patient with carotid artery disease in terms of both early and late restenosis potentials. Previous work (33) has demonstrated this result to hold true even when a vein patch is used rather than PTFE. Early carotid restenosis is usually caused by myointimal hyperplasia, which is thought to be a response to mechanical injury to the arterial wall (15, 51, 62). Such an injury can come from the CEA itself or the action of internal blood pressure and flow that interact with the endarterectomized wall. Our analysis showed that mechanical stresses produced by blood pressure were significantly smaller for CEE than for CEAP, even when stresses on the patch surface were excluded from comparison. The reason for this is likely twofold. First, the oblique arteriotomy of CEE acts favorably in decreasing mechanical stress compared with longitudinal arteriotomy of CEAP. Second, the mismatch in properties between the PTFE patch and the host arterial wall produces high-stress concentrations at the patch-artery interface and causes the more compliant posterior native arterial wall to bulge out, resulting in high ES. The finding of high-stress concentrations with CEAP is consistent with the clinical findings of Rosenthal et al. (50), who demonstrated higher incidence of post-CEA restenosis at the level of the bulb in patients with CEAP.

Repair of the artery with a stiff PTFE patch also restrained wall deformations, resulting in lower CS for CEAP compared with CEE. In the case of CEAP, however, high-CS concentrations were mainly observed at the suture ends, which may cause additional injury around the patch boarders and push the healing process toward a restenotic phenotype. In CEE repair, high CS was mostly concentrated around the anterior-posterior bend and was a consequence of normal straightening of the artery during pulsation.

In terms of hemodynamics associated with late restenosis, CEE also showed superior results compared with CEAP. Late restenosis is usually due to the progression of atherosclerosis, which is thought to be associated with low and oscillatory shear stress and long T_r (12–14, 20, 43). In our study, zones of low and oscillatory WSS were present in both CEE and CEAP, but in the case of CEAP, this zone was larger due to a wider bulb and a more acute transition from the patch to the native artery. The carotid bulb is notorious for atherosclerotic inflammation (38). Due to an abrupt change in the curvature and a sudden increase in the cross-sectional area at the carotid bulb, high-momentum blood is incapable of instantaneously changing direction to accommodate the curvature. This is most pronounced during the decelerative phase of systole, when the flow exhibits boundary layer separation and formation of VSs (67). This leads to lower blood velocity and WSS and longer T_r at the carotid bulb.

Elevated shear stress, on the other hand, can be protective within the physiological range [>1–2 Pa (43) but <40 Pa (25)], and, as a consequence, the proximal CCA, distal ICA, and ECA are generally less frequently affected by atherosclerosis. At the same time, excessively high shear may lead to platelet activation (52), especially in the absence of antagonists from the altered endothelial layer. This activation may be fostered by the formation of VSs that trap platelets inside during systole and release them upon suppression of the vortex at diastole. These activated and released platelets may then travel to the low-WSS and low-velocity areas downstream, where the endothelial phenotype switches from atheroprotective to atherogenic (43), and activated platelets have more time to deposit on and into the arterial wall (7, 33). The effect of low shear has been extensively studied and is now thought to include mediated recruitment of monocytes, increased vasoconstriction and paracrine growth stimulation of vessel wall constituents, increased oxidant state, and increased apoptosis and cellular turnover (43).

In clinical practice, there has not been convincing evidence that univocally demonstrates better outcomes in terms of stroke, late restenosis, or the location of restenosis for CEE compared with CEAP. Four previous prospective randomized trials have compared CEE with CEAP (2, 3, 11, 63). Half of these showed relatively lower combined restenosis and occlusion rates with CEE (2, 3), whereas the other half showed no difference (11, 63). The two studies that showed benefits of CEE versus CEAP considered bilateral repair, therefore eliminating the influence of systemic risk factors associated with patient demographics. Retrospective studies comparing the two reconstruction techniques have also either shown similar or lower restenosis rates for CEE (16, 36, 39). Although restenosis rates after CEA are relatively low, it still does affect between 1% and 5% of patients and many times leads to more risky and expensive reintervention. As a prohibitively large sample size would be required to perform a satisfactorily powered prospective clinical trial to detect meaningful differences in restenosis rates (10), other methods must be used to help determine the optimal operative technique. Mathematical modeling of arterial repair with in silico CEAP and CEE can be helpful in this regard.

In conclusion, for the average patient with carotid artery disease, our in silico analysis demonstrated that carotid endarterectomy performed with the eversion technique may offer potential hemodynamic benefits over endarterectomy with patch angioplasty. Although other factors may influence patient selection and outcomes, with further experimental and clinical validation, in silico arterial modeling holds promise to help better inform surgeons and patients regarding the hemodynamic benefits and drawbacks of different reconstructive techniques.

GRANTS

This work was supported in part by National Institute on Aging Grant R01-AG-034995 and by grants from the Nebraska Research Initiative Nanofiber Core Facility, the National Science Foundation, the University of Nebraska-Lincoln/University of Nebraska Medical Center Engineering for Medicine initiative, and the Charles and Mary Heider Fund for Excellence in Vascular Surgery.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: A.V.K., I.I.P., Y.A.D., and J.N.M. conception and design of research; A.V.K., I.I.P., and J.N.M. performed experiments; A.V.K., I.I.P., P.K.G., and J.N.M. analyzed data; A.V.K., I.I.P., Y.A.D., P.K.G., S.A.J.K., and J.N.M. interpreted results of experiments; A.V.K. prepared figures; A.V.K., I.I.P., and J.N.M. drafted manuscript; A.V.K., I.I.P., Y.A.D., P.K.G., S.A.J.K., and J.N.M. edited and revised manuscript; A.V.K., I.I.P., Y.A.D., P.K.G., S.A.J.K., and J.N.M. approved final version of manuscript.