A closure scheme for chemical master equations

Abstract

Probability reigns in biology, with random molecular events dictating the fate of individual organisms, and propelling populations of species through evolution. In principle, the master probability equation provides the most complete model of probabilistic behavior in biomolecular networks. In practice, master equations describing complex reaction networks have remained unsolved for over 70 years. This practical challenge is a reason why master equations, for all their potential, have not inspired biological discovery. Herein, we present a closure scheme that solves the master probability equation of networks of chemical or biochemical reactions. We cast the master equation in terms of ordinary differential equations that describe the time evolution of probability distribution moments. We postulate that a finite number of moments capture all of the necessary information, and compute the probability distribution and higher-order moments by maximizing the information entropy of the system. An accurate order closure is selected, and the dynamic evolution of molecular populations is simulated. Comparison with kinetic Monte Carlo simulations, which merely sample the probability distribution, demonstrates this closure scheme is accurate for several small reaction networks. The importance of this result notwithstanding, a most striking finding is that the steady state of stochastic reaction networks can now be readily computed in a single-step calculation, without the need to simulate the evolution of the probability distribution in time.

The fabric of all things living is discrete and noisy, individual molecules in perpetual random motion. However, humans, in our effort to understand and manipulate the biological cosmos, have historically perceived and modeled nature as large collections of molecules with behaviors not far from an expected average. Mathematical models, founded on such determinism, may be excellent approximations of reality when the number of molecules is very large, approaching the limit of an infinitely sized molecular population (1–5). Of course, the size of biomolecular systems is far from infinite. And we know that the behavior of a few molecules fluctuating from the average in unexpected ways may forever seal the fate of a living organism. It has thus been commonly recognized that models of small, evolving molecular populations better account for the noisy, probabilistic nature of outcomes (6–8).

The most complete model of stochastically evolving molecular populations is one based on the master probability equation (9). The “master” in the name reflects the all-encompassing nature of an equation that purports to govern all possible outcomes for all time. Because of its ambitious character, the master equation has remained unsolved for all but the simplest of molecular interaction networks, even though it is now over seven decades since the first master equations were set up for chemical systems (10, 11). Herein we present a numerical solution to master equations of small chemical or biochemical reaction networks.

We first explain why efforts to solve the master equation have been thwarted to date, and define master equations briefly. In general, for a system of N molecular species, the state of the system is described by an N-dimensional vector 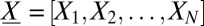, where 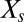is the number of molecules of species s. The master equation governs the evolution of the probability, 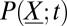, that the system is at state 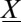at time t:

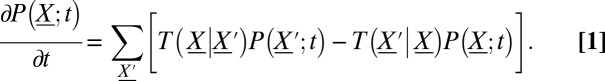This is a probability conservation equation, where 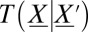is the transition propensity from any possible state 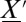to state 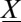per unit time. In a network of chemical or biochemical reactions, the transition probabilities are defined by the reaction-rate laws as a set of Poisson-distributed reaction propensities; these simply dictate how many reaction events take place per unit time.

The reason analytical solutions to the chemical master equation remain elusive becomes clear when the master equation is recast in equivalent terms of probability moments: the probability distribution average, the variance, and so on:

where 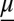is the vector of moments up to order M, and A is the matrix describing the linear portion of the moment equations. On the right, 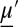is the vector of higher-order moments, and the corresponding matrix 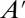. Generating the matrices in Eq. 2 can be performed either analytically (12, 13) or numerically (14). For linear systems with only zeroth or first-order reactions, 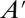is empty. For other systems, 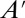is not empty and Eq. 2 becomes infinitely dimensional, and thus intractable. Note that Eq. 2 assumes reaction networks are comprised of only polynomial reaction-rate laws, as described in ref. 14.

To use Eq. 2, a closure scheme must be defined. A closure scheme approximates the infinite set of moment equations with a finite one that accepts a solution. Typically, a closure scheme is an approximation:

where F is a function that uses the lower-order moments to approximate the higher-order moments. There have been numerous attempts to define F, either by assuming an underlying distribution (12, 15, 16) or through numerical approximation (17–19). However, closure schemes thus far exhibit limited accuracy and uncertain utility.

An alternative approach of modeling stochastically evolving molecular populations is based on the numerical sampling of the probability distribution. Gillespie developed the stochastic simulation algorithm (SSA) in the 1970s. This is a kinetic Monte Carlo method that generates ensembles of stochastic trajectories in state space (20). Although this algorithm and the numerous improvements have found ample use by an ever-widening community (21, 22), this approach becomes cumbersome when reaction rates span multiple time scales. Furthermore, this approach does not facilitate important analysis methods, such as steady-state and stability analysis, or perturbation and bifurcation analysis, which are useful in the study of evolving molecular systems.

Herein we present a closure scheme that is accurate and may be implemented on reaction networks with reaction rates of higher order than one. The proposed method affords the determination of how reaction networks evolve in time, when away from the thermodynamic limit—that is, when the molecular population size is infinite—offering an alternative to kinetic Monte Carlo sampling methods. Perhaps more importantly, this formulation facilitates the calculation of steady-state probability distributions of reaction networks without resorting to dynamic simulations. As such, it may facilitate the type of analysis of dynamic or steady states that is either impossible or impractical using kinetic Monte Carlo techniques. It should be noted that the present incarnation of the method necessitates the determination of probabilities at all relevant states in the state space and thus scales poorly as the reachable state space expands.

Zero-Information Closure Scheme

For the sake of brevity, we limit the discussion in this section to one-dimensional state spaces. In particular, for a single random variable that can attain a discrete set of values, 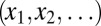, each with probability 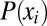, the information entropy is defined as (23):

We conjecture that a finite number of probability moments may capture all of the information needed to precisely construct the probability distribution. In consequence, we maximize the information entropy under the constraints of the first M moment definitions:

where is the Lagrange multiplier of the jth moment constraint. These are readily computed with appropriate root-finding numerical methods, such as the simple Newton–Raphson method we present in the SI Appendix, section S1.

Trivially, the final form for the maximum-entropy probability distribution is (24):

Now the –th order moment can be computed from the maximum entropy distribution:

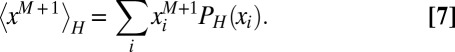Eqs. 2 are now closed and can be integrated to evolve the probability moments by a time step 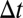. Given an initial condition for the value of the probability moments, the system may be propagated in time. With newly calculated moments up to order M, the information entropy is maximized again, generating new values for the Lagrange multipliers, and so on.

It is important to note that, in a separate calculation without simulations in time, the steady state of reaction networks can be computed by determining the most likely distribution moments that lie in the null space of the augmented matrix 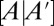. This means that the steady-state moments are found so that they maximize the information entropy as well as satisfy:

We note that in this calculation there is no need to provide an initial condition for the probability distribution in state space. Because only a single optimization step is used this method is far more efficient than traditional Monte Carlo approaches.

The algorithm that couples the optimization with the ODE solver, and the algorithm for determining steady-state probability distributions are detailed in the SI Appendix, sections S2 and S3.

Models

To illustrate the utility of the closure scheme (henceforth called ZI closure) in generating both dynamic trajectories and steady-state results, we investigate three models, described in Table 1. Model 1 represents a simple reversible dimerization reaction network with a second-order reaction. There is a single independent component, A, as conservation arguments can be used to eliminate B. Model 2 represents a Michaelis–Menten reaction network (25). There are two independent components, the substrate S and the enzyme E. Model 3 represents the Schlögl model (26), a four-reaction network that can produce bimodal distributions. There is a single free component, X, and two reservoirs, A and B, assumed constant. It may be noted that the values for A and B are incorporated into the first and third reaction-rate constants whenever specified. All systems are considered isothermal, well mixed, inside a volume L, a typical size for common bacteria. In all cases the initial conditions in Table 1 define the initial probability distributions as Kronecker delta functions. For example, for model 1, 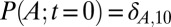.Comparisons of dynamic and steady-state results are made between the ZI-closure method and the widely used SSA improvement prescribed by Gibson and Bruck (21).

Table 1.

Model description for comparison of ZI closure to SSA

Model	Reversible dimerization	Michaelis–Menten	Schlögl
Reactions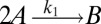
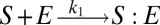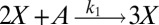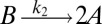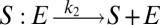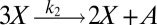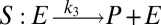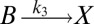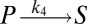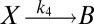Degrees of freedom	A	S, E	X
Initial condition		;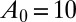

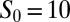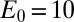
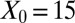Although it is understood that the chosen models are simple, the presence of second- and higher-order reactions necessitates moment closure (i.e., matrix 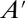is not empty). Here, we use these models to show that the proposed closure scheme meets three important goals. First, the method remains accurate regardless of the separation of time scales in the reaction rates. Second, the method remains valid for systems with multiple degrees of freedom. Third, the method is accurately implemented for higher-order closures (e.g., 12th-order closure is successfully implemented for the Schlögl model).

Results and Discussion

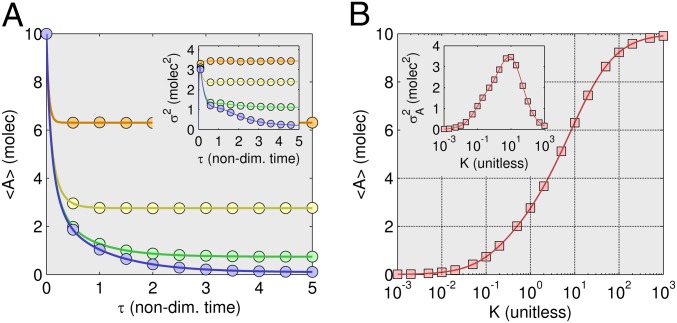
The time trajectory is shown in Fig. 1A for the average and the variance (Inset) of the number of A molecules in model 1, as calculated with ZI closure. The results are also shown for the stochastic simulation algorithm, as improved by Gibson and Bruck (21) and implemented in Hy3S, an open-license software package for simulating stochastic reaction networks (22). In all comparisons the results are shown for 10⁶ SSA trajectories, unless otherwise stated.

Fig. 1.

Dynamic trajectory and steady-state results for reversible nonlinear dimerization. (A) Evolution of the average and variance (Inset) of number of A molecules using fourth-order ZI closure. Different symbols represent various values of equilibrium constant K = k₂/k₁. The forward reaction rate is constant at k₁ = 1 (1/molecules-s). The initial distribution for the trajectory results is a Kronecker-delta function, 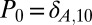. Solid lines are from fourth-order ZI closure and circles are results from 100,000 SSA trajectories. Colors refer to dissociation constants with orange (K = 10), yellow (K = 1), green (K = 0.1), and blue (K = 0.01). (B) Steady-state results for a range of K values using fourth-order ZI closure (line), compared with SSA results (squares). The 10,000 k₂ values were modeled ranging from 10⁻³ to 10³ (1/s) [k₁ = 1 (1/molecules-s) SSA results for 20 k₂ values, each with 100,000 trajectories. The variance results are shown in the Inset.

Four distinct dynamic trajectories are shown for different equilibrium constant values spanning four orders of magnitude. The comparison is favorable between the ZI-closure method and the SSA. It is interesting to find that although at the extremes of equilibrium constant K values, second-order closure is adequate, the match becomes relatively poor when k₁ is equal to k₂ (SI Appendix, Fig. S1). Despite the simplicity of model 1, fourth-order closure is necessary for accurate results across all studied kinetic values. This presents a major advantage of ZI closure over previous closure schemes, most all of which cannot be assumed to remain accurate as closure order is increased to an arbitrarily high order.

We note that the ZI-closure scheme is not as computationally efficient as the SSA is for simulating the dynamic evolution of reaction networks. This drawback is due to the computationally taxing optimization step present at each time step. There may be benefits in using the ZI-closure method for stiff reaction networks, but exploring these is beyond the scope of the present manuscript.

The steady state of model 1 is shown in Fig. 1B across seven orders of magnitude for the kinetic constant (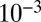 to 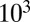). Again, fourth-order closure accurately describes the mean and variance for all constant values (SI Appendix, Fig. S2). Steady-state results are produced quickly, because only a single optimization step is needed. For demonstration purposes, we calculated 10,000 steady states varying the equilibrium constant value. Simply put, this is implausibly many points for SSA to compute. As such, these results suggest a use of ZI closure in accurately and efficiently performing steady-state and sensitivity analysis of stochastic reaction systems, important topics that have only seen slow progress in the past.

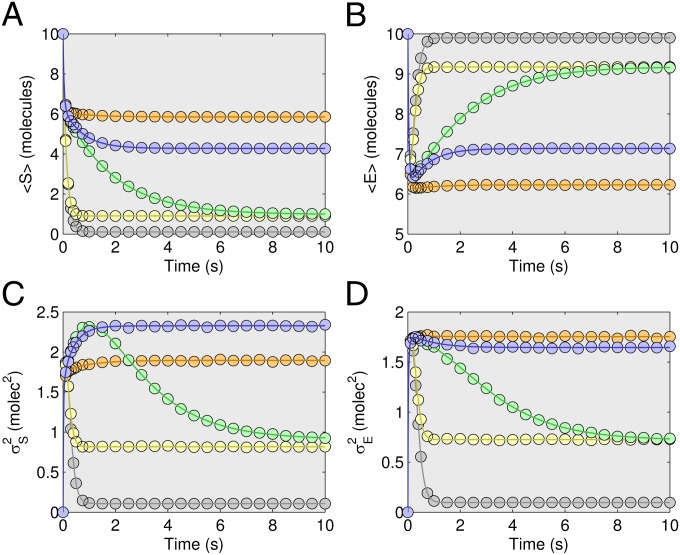
We also tested the ZI-closure scheme for the Michaelis–Menten model. In Fig. 2, the evolving average and variance for molecules S and E are shown for a range of kinetic constants. Additional results are provided in the SI Appendix for kinetic constants across three orders of magnitude (SI Appendix, Fig. S3).

Fig. 2.

Michaelis–Menten trajectory results. For the Michaelis–Menten model, 27 combinations of free parameters were simulated. Shown here are the average number of species E and species S (plots A and B, respectively), and the variance of species E and species S (plots C and D, respectively) for five of these combinations. Results from ZI closure in solid lines and from SSA as circles. Colors refer to different kinetic rates with gray ([k₂, k₃, k₄] = [1, 10, 0.1] 1/s); orange ([k₂, k₃, k₄] = [10, 0.1, 1] 1/s); yellow ([k₂, k₃, k₄] = [0.1, 10, 1] 1/s); green ([k₂, k₃, k₄] = [10, 1, 0.1] 1/s); and blue ([k₂, k₃, k₄] = [10, 1, 1] 1/s). The initial distribution is a Kronecker-delta function, .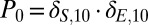

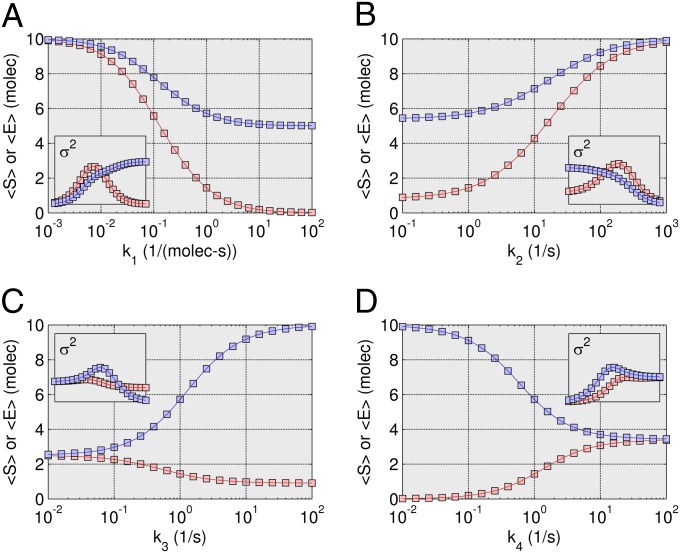
Steady-state results for the Michaelis–Menten model are presented in Fig. 3 for a wide range of the four kinetic parameters over multiple orders of magnitude. Evidently, the ZI-closure steady-state optimization algorithm is applicable to multicomponent systems. Again, the steady-state results were produced relatively quickly compared with the SSA. The Michaelis–Menten results in particular demonstrate that this type of optimization may be used efficiently to perform sensitivity analysis. The slopes of the trajectories are equivalent to sensitivities of the mean and variance of the steady-state distribution to the four kinetic constants. Here again we observe that although second-order ZI closure is for the most part adequate, it diverges slightly in several cases. In all cases fourth-order ZI closure is accurate (SI Appendix, Fig. S4).

Fig. 3.

Steady-state results for Michaelis–Menten model. The steady-state results for a wide range of kinetic parameter values [centered around k₁ = 1 (1/molecules-s), k₂ = 1 (1/s), k₃ = 1 (1/s), and k₄ = 1 (1/s)] for the Michaelis–Menten model (S₀ = 10; E₀ = 10). (A) Both the mean substrate (S, red) and enzyme (E, blue) count are shown for fourth-order ZI closure (solid lines) and compared with SSA simulations (squares) with one million trajectories. (B–D) Identical conditions as in A except for k₂, k₃, and k₄, respectively. Note that as each parameter is ranged in A–D the rest are held constant. Insets show variances for S (line for ZI closure, circle for SSA), and E (line for ZI closure, square for SSA).

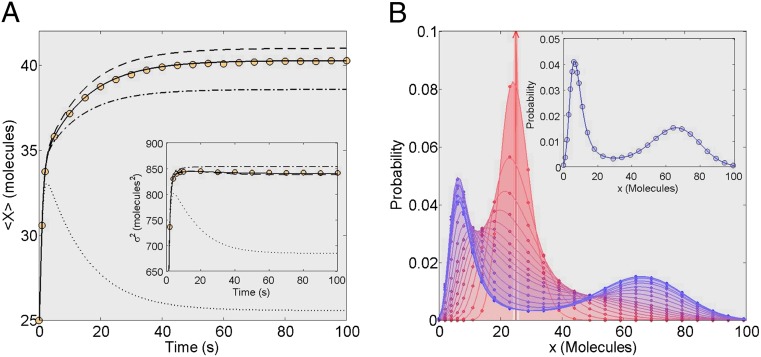
Fig. 4A shows the time trajectories for the Schlögl model with kinetic constants chosen to result in extreme bimodality (Fig. 4B, Inset). This complex network was chosen because many moments are necessary to accurately describe the system evolution. The results clearly demonstrate how ZI-closure can accurately capture even complex distributions. Fig. 4A shows 6th-, 8th-, 10th-, and 12th-order ZI closure compared with results of one million SSA trajectories. It is demonstrated that 12th-order closure is necessary to accurately match the mean of the SSA trajectories. These results show that the ZI-closure scheme is able to achieve accuracy even when high-order closure is necessary. SI Appendix, Fig. S5 provides additional time trajectory data.

Fig. 4.

Schlögl model trajectory results and steady-state distribution. The ZI-closure trajectory results for the Schlögl model [k₁ ⋅ A = 0.15 (1/molecules-s), k₂ = 0.0015 (1/molecules²-s), k₃ ⋅ B = 20 (molecules/s), and k₄ = 3.5 (1/s)]. The initial distribution is a Kronecker-delta function, 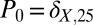. (A) The mean output of X through time; for 6th-order ZI closure (dotted line), 8th-order ZI closure (dot–dash line), 10th-order ZI closure (dashed line), and 12th-order ZI closure (solid line). The trajectories are compared with one million SSA trajectories (circles). Inset shows corresponding variance results. (B) To demonstrate how this method replicates the actual underlying distribution found using 12th-order ZI closure (lines) is plotted with the SSA-simulated distribution (circles). Time flows from red to blue, demonstrating good reproduction of the actual underlying distribution throughout time. Inset compares the steady-state 12th-order ZI closure (line) to the steady-state SSA distribution (circles).

Fig. 4B shows the probability distributions through time for both 12th-order ZI closure and the SSA. The distributions computed with ZI closure match the actual SSA distributions remarkably well throughout time. These results provide a most convincing argument for ZI closure as a powerful closure scheme. Indeed, the bimodal distribution of the Schlögl model is particularly challenging to simulate. SI Appendix, Fig. S6 shows steady-state probability distributions using lower-order closure, illustrating the poor fit of lower-order closures.

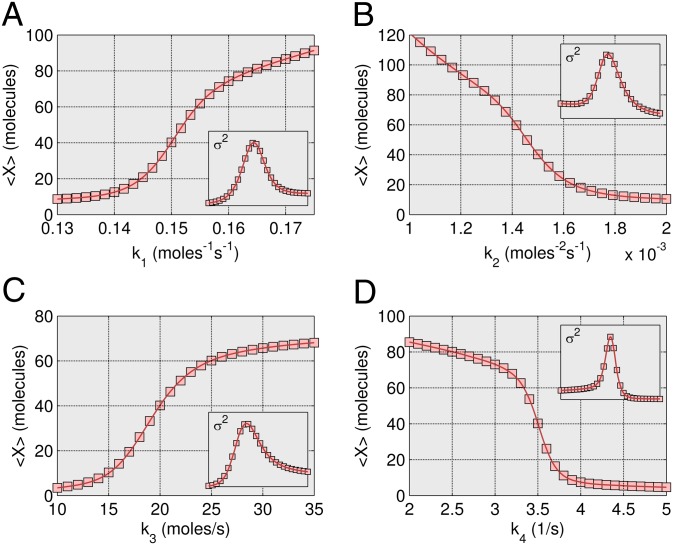
Steady-state results are presented in Fig. 5 for the Schlögl model over a wide range of values for the four kinetic constants. Only the 12th-order closure is shown for the mean and variance results compared with SSA results. A quantitative sensitivity analysis is now possible, investigating the impact of kinetic constants on the behavior of the network. The steady-state optimization method renders a thorough analysis feasible, where none was previously available. Sampling the probability distribution with SSA quickly becomes untenable because of the combinatorial explosion of necessary trajectories. (Additional lower-order closure data are provided in SI Appendix, Fig. S7).

Fig. 5.

Steady-state Schlögl model results. Sensitivity analysis where the four kinetic constants are varied around the values used in the trajectory simulation such that the entirety of the bimodal region is represented. (A) The mean steady-state output of X was simulated for 450 k₁ ⋅ A values between 0.13 and 0.175 (1/molecules-s) using a 12th-order ZI closure (line), and compared with 28 points simulated using an SSA (squares). (B) Results for 200 k₂ values between 0.001 and 0.002 (1/molecules²-s) using a 12th-order ZI closure (line), compared with 25 points simulated using an SSA (squares). (C) Results for 250 k₃ ⋅ B values between 10 and 35 (molecules/s) using a 12th-order ZI closure (line), compared with 25 points simulated using an SSA (squares). (D) Results for 300 k₄ values between 2 and 5 (1/s) using a 12th-order ZI closure (line), compared with 30 points simulated using an SSA (squares). Insets show variance comparisons.

For all of the appeal of the ZI-closure scheme, drawbacks exist. First, in its present form, the algorithm tends to be less efficient in producing trajectories through time than SSA. This is because optimization, the complexity of which scales with the state-space size, is needed in every time step. Second, the number of moment equations scales as 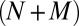choose M, although ODE or stochastic differential equation models for chemical networks scale with the number of components, N. This challenge inherently limits all moment closure schemes, and it likely limits the utility to relatively small networks until large-scale algorithms are developed. Finally, ZI closure, in its present form, faces numerical implementation challenges, in particular when delta functions best describe the probability distributions. At this limit the λ parameters diverge to infinity, although, in principle, starting from a multivariate Gaussian distribution addresses this drawback.

Conclusions

Since the days of Newton and Leibnitz, mathematical models have been at the heart of physical and engineering sciences. Founded on universally accepted physicochemical laws, these models capture the essential aspects of systems, phenomena, and processes, all in a way fit for analysis, explanation, understanding, and then for design, engineering, optimization, and control.

There are many reasons why mathematical models are not presently at the heart of biological sciences. To name a few: we are still discovering the parts that comprise living organisms; there are very many of these components; the kinetic parameters and thermodynamic strength of interactions are not known, or at least not known in all relevant contexts; there are environmental, exogenous dependencies that dictate biological behaviors; there are evolutionary, historical links that determine the nature of biosystems. They all impose significant epistemological hurdles, let alone the practical ones involved in reliable model development.

Another important challenge facing scientists is related to capturing random molecular events that determine all too frequently the fate of a living organism. It has been argued that probabilistic fluctuations are a defining feature of biomolecular systems, conferring necessary elasticity under environmental stresses. Living organisms can then explore a distribution of states with finite probability. As a result, stochastic outcomes become a double-edged sword: they equip a population of organisms with adaptation potential under evolutionary pressures, but they may also doom an individual organism.

The modeling framework for capturing probabilistic outcomes in evolving molecular populations has been cast for over seven decades with the work of Delbrück and McQuarrie on chemical master equations. However, a solution has been elusive thus far, when there are second- or higher-order reactions. It is inconceivable to describe biomolecular systems without the presence of interacting molecular partners. In consequence, master equations have not inspired biological discovery.

Here we presented the ZI closure scheme for master probability equations that govern the evolution of small molecular populations reacting with reaction rates of order higher than one. We demonstrate progress in three main areas. First, ZI closure works on single or multicomponent reaction networks. Second, ZI closure is applicable across a wide range of kinetic parameters in simple models. Third, ZI closure can be applied for high-order closure with commensurate accuracy gains.

ZI closure represents a closure scheme that renders the moment viewpoint a viable alternative to kinetic Monte Carlo methods for stochastic chemical simulation. Although beyond the scope of the current study, more efficient algorithms with improved or guaranteed convergence can be developed. ZI closure may then supplant the SSA for stochastic chemical simulations, especially for small reaction networks.

Importantly, ZI closure represents a unique method for determining steady-state distributions without having to simulate reaction networks through time. ZI closure requires only a single optimization step to determine steady-state distributions. This is significantly more efficient than kinetic Monte Carlo simulations. As such, ZI closure facilitates the use of many well-defined deterministic analysis tools previously considered impractical for stochastic systems. Even in its present form the method can be used to investigate eigenvalue problems, to determine more accurate bifurcation diagrams for small systems, and quickly analyze small networks.

We believe these results to be of special importance with utility in the biological sciences. For example, with a microscopic definition of irreversible processes, a wide range of experimental observations of biomolecular interactions may be mathematically conceptualized. As a result, general principles and laws that govern biological phenomena may ultimately be established.