Figure 3.

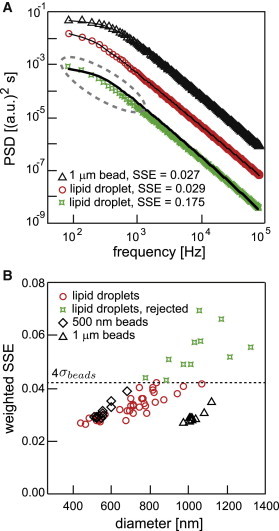
The goodness of fit to the PSD of the droplets reveals that most lipid droplets are spherical and homogeneous. (A) PSD plots of the thermal motion of an optically trapped 1-μm-diameter polystyrene bead (black triangles) and the thermal motion of optically trapped lipid droplets (red circles and green stars). Analytical fits of the full hydrodynamic theory for the diffusion of a spherical particle in a harmonic potential are shown as black lines. By visual inspection, it is clear that the theory fits the PSD of the bead (black triangles) and that of the first lipid droplet (red circles) very well, but it fails to fit the PSD of the second droplet (green stars). The PSD of an aspherical particle is elevated at low frequencies (dashed ellipse) and can no longer be correctly fit by the analytical theory. The traces indicate that the first droplet was as spherical and homogeneous as the polystyrene bead, whereas the second droplet was not. (B) The weighted SSE of the fit of the analytical theory to the PSD as shown in A is plotted versus diameter for lipid droplets (red circles and green stars) and reference beads of 500 nm diameter (black squares) and 1 μm diameter (black triangles), where the diameter was determined from the fit. Most droplets have SSEs comparable to the SSEs of the reference particles. The larger the droplet, the more likely it is to have a high SSE. We empirically set a cutoff at <SSE_beads> + 4σ_beads (dashed line). Droplets with SSEs above this cutoff were discarded and not used in further analysis.