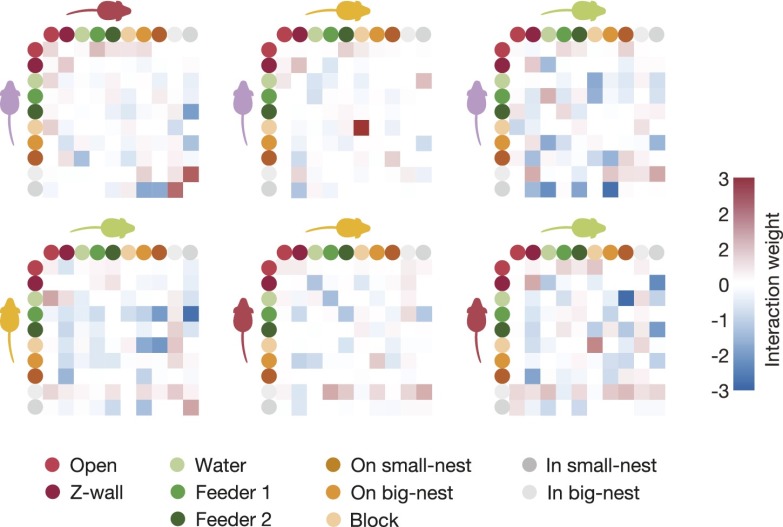
Figure 4. Functional social interaction maps between mice.

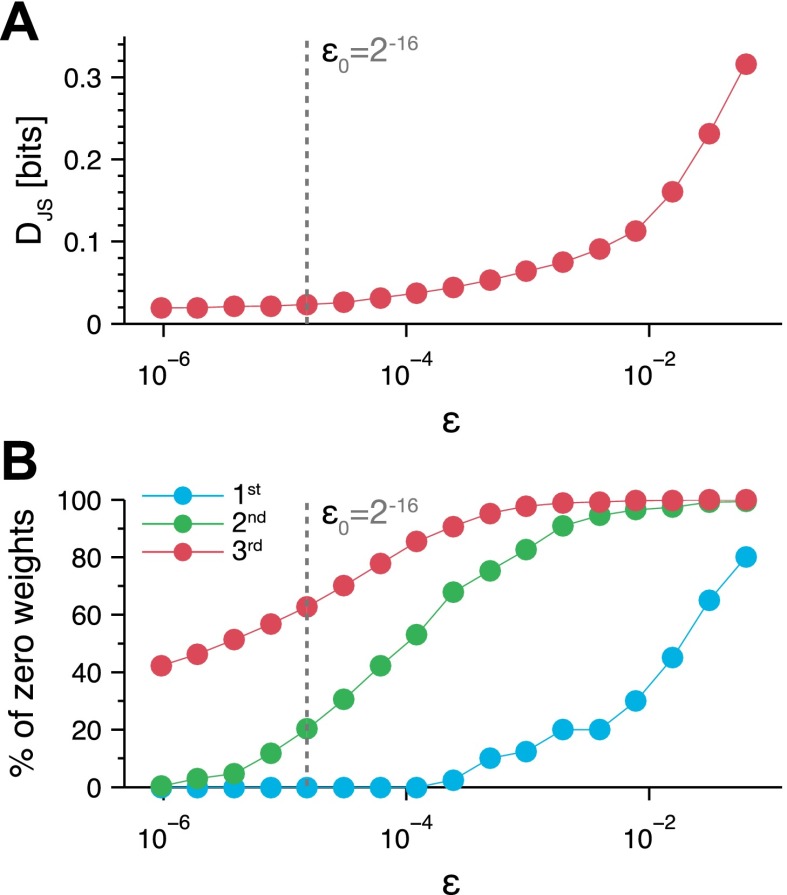
(A) Accuracy of a ‘regularized’ third-order maximum entropy model of the spatial configurations of the same groups of mice from Figure 3A. Model predictions are plotted against the empirical distribution. For details of parameter selections for the regularized model see Figure 4—figure supplement 1. (B) The distribution of ME parameters according to the order of interactions in the regularized p^* model (shown above the horizontal line), compared to the model without regularization (shown below the line). The distribution is over parameters of all eight groups of SE mice taken together. (C) Full pairwise interaction maps for four representative groups. (Group S2 is magnified as it is used in following panels.) In each of these maps, the colored dots represent the location of a mouse according to the color coding in the bottom of the figure. The colors of the mice are depicted near their corresponding locations. The color of a vertex shows whether the interaction is positive (red) or negative (blue) and its width reflects the interaction strength. An alternative presentation of all the pairwise interaction parameters is shown in Figure 4—figure supplement 2. (D) The dominant positive and negative pairwise interactions are shown overlaid on a diagram of the arena. ‘Filled mice’ show positive interactions, and ‘empty mice’ show negative interactions. A star denotes that the mouse is on the nest. The value of the corresponding interaction is shown on the bottom of each panel. (E) The dominant positive and negative triplewise interactions for the same group as in D, overlaid on a diagram of the arena.

DOI: http://dx.doi.org/10.7554/eLife.00759.008

Figure 4—figure supplement 1. Tradeoff between generalization and accuracy of the maximum entropy model.

We found the 3^rd order maximum entropy model for the mice configurations, with an additional penalty term that minimized the number of non-zero parameters (see Materials and methods). The balance between maximizing the model's entropy and minimizing the penalty is controlled by parameter ∈. (A) The effect of the tradeoff parameter on the accuracy of the model is shown as the Jensen–Shannon divergence (DJS) between the third order maximum entropy model with the penalty term and the model without the penalty term (as in Figure 3). The Jensen–Shannon divergence equals 0 when the two models are identical, and would be 1 at its maximal value—when the two distributions are distinct. The results are from the second day of the same group as in Figure 3a. (B) The fraction of parameters that equal zero is shown for each order (1^st, 2^nd and 3^rd order parameters of the maximum entropy model) is shown as a function of ∈. The chosen value ${\in }_0=2^{-16}$, which we used in Figure 4 is marked by a dashed line on the graphs.

DOI: http://dx.doi.org/10.7554/eLife.00759.009

Figure 4—figure supplement 2. All pairwise interactions of a typical group.

These interactions are the weights of the second-order interactions in the regularized third-order maximum entropy model. Each panel corresponds to one pair of mice, and its rows and columns correspond to the locations within the arena according to the legend at the bottom of the figure.

DOI: http://dx.doi.org/10.7554/eLife.00759.010