Protein Charge and Mass Contribute to the Spatio-temporal Dynamics of Protein-Protein Interactions in a Minimal Proteome

Abstract

We constructed and simulated a ‘minimal proteome’ model using Langevin dynamics. It contains 206 essential protein types which were compiled from the literature. For comparison, we generated six proteomes with randomized concentrations. We found that the net charges and molecular weights of the proteins in the minimal genome are not random. The net charge of a protein decreases linearly with molecular weight, with small proteins being mostly positively charged and large proteins negatively charged. The protein copy numbers in the minimal genome have the tendency to maximize the number of protein-protein interactions in the network. Negatively charged proteins which tend to have larger sizes can provide large collision cross-section allowing them to interact with other proteins; on the other hand, the smaller positively charged proteins could have higher diffusion speed and are more likely to collide with other proteins. Proteomes with random charge/mass populations form less stable clusters than those with experimental protein copy numbers. Our study suggests that ‘proper’ populations of negatively and positively charged proteins are important for maintaining a protein-protein interaction network in a proteome. It is interesting to note that the minimal genome model based on the charge and mass of E. Coli may have a larger protein-protein interaction network than that based on the lower organism M. pneumoniae.

Introduction

The cell is a collection of well-organized protein machines [1], with the biological processes working together to maintain life. Charge is necessary for protein solubility, ligand interaction, and essentially all protein functions [2]. Many cellular functions rely on the electrochemical structure in the crowded cytoplasm, and the distributions of charged macromolecules (proteins and RNAs) define the electrochemical macro-environment. Consequently, cellular metabolite concentrations are proportional to the magnitude of the charged surface areas and hydrophobicity [3]. Proteins have no net charge at their Isoelectric points (pI). Most of the proteins’ pI values are not near physiological pH (around 7). The distributions of the proteins’ pI values in proteomes are bimodal: one set for acidic proteins and another for basic proteins. The bimodal pI distribution in the proteome is universal for all organisms, probably due to either amino acid pKa values [4, 5] or to the organism function [6-8]. The relative abundances of acidic and basic proteins differ among species. It is interesting to note that for small proteomes, there is a negative correlation between the proteome size and the average pI of the proteins; i.e., small proteomes tend to have more basic proteins [6, 8].

Protein networks are spatially organized to save diffusion-collision times in the large cell. Proteins often cluster together to perform certain functions, for example, by forming transcriptional factories [9]. Signal transduction occurs in an organized microenvironment, where elements of a signaling pathway are connected functionally and spatially [10, 11]. Consequently, the organization of proteins with different charges and sizes can be important to allow fast cellular response in fluctuating environments. It is however still unclear how nature accomplishes the arrangement. At one end of the spectrum is gene fusion which links covalently two (or more) proteins; at the other are compartmentalization and protein-protein interactions. Here we focus on a possible role of charge distributions and how these can affect the spatio-temporal dynamics of proteins and the protein-protein interaction (PPI) network. The PPI network coordinates cellular functions. Signals travel through the membrane to the cell interior, and are typically relayed through interaction partners [12]; thus, the spatio-temporal dynamics of proteins in a proteome underlies signaling pathways and plays a key role in functional control [13]. Experimental investigation of the spatio-temporal dynamics of proteins progresses rapidly: the global expression of proteins in yeast has been largely characterized, including the concentrations of most proteins [14]. Cryo-electron tomography has reached a visual resolution of 4-5 nm, helping in the localization of macromolecules in the cell [15]. Nanoscopic features of cellular structures at 20-50 nm resolution can be probed by stochastic optical reconstruction microscopy [16]. The PPI network of conserved and essential proteins in E. coli has been characterized [17], along with quantitative data on the proteome abundance and noise at the single-cell level [18]. These help in understanding the spatio-temporal dynamics of proteins and their networks.

Computational studies have also provided insight into the spatio-temporal dynamics of proteins and the PPI network. Particles at various resolutions were employed to simulate cell-like environments, with or without physics-based interactions [19]. Cytoplasmic proteins have been grouped into beads with different masses in Ellison’s coarse-grained model [20] and in the work of Bicout and Field [21]. Ando and Skolnick studied a cytoplasm model comprised of 15 different macromolecules, using beads to represent proteins and nucleic acids [22]. McGuffee and Elcock [23] developed an atomistically detailed Brownian dynamics (BD) simulations for the bacterial cytoplasm, comprising of 50 different types of the most redundant macromolecules. Other atomistically detailed BD simulations have also been reported [18, 23, 24]. Similarly, Wade et al. reported a novel atomic-detailed methodology to simulate protein solutions [25].

In this work, we investigated the charge distribution in a minimal proteome and its effects on the spatio-temporal dynamics of proteins and their interaction network. Several small cells have been well characterized experimentally. Mycoplasma genitalium was the species with the smallest number of genes known, with 470 proteins [26, 27]. M. pneumoniae is also among the smallest known self-replicating bacteria [28]. M. pneumoniae has only 690 ORFs. The copy numbers of 413 proteins (59.9% of the total predicted proteome) have been quantified recently [29]. The growth rates of these smallest cellular systems were very slow. With a slightly larger genome, 1.08-mega-base pair Mycoplasma mycoides were successfully designed, synthesized, and assembled into new cells which are capable of continuous self-replication [30]. The above cellular systems can be excellent references to compare with the potential minimal proteome. In selecting the minimal proteome, we did not intend to reproduce specific prokaryotic or eukaryotic organisms. Instead, we focus on the characteristics of a polydisperse collection of a possible minimal proteome in a cellular environment. Ideally, the selected minimal proteome can capture the common features of different organisms. The smallest set of the proteome of a minimal genome can be compiled from the literature [31], which is comprised of 206 kinds of essential proteins. We map the protein concentrations from experimentally measured results in a complete yeast proteome [14] as well as in the E. coli proteome [18, 22]. Then, we develop a coarse-grained model to describe protein molecules using spherical nanoparticles with electronic and van der Waals interactions. By simulating the minimal proteome with Langevin dynamics, we are able to reveal that ‘proper’ distributions of negatively and positively charged proteins are important for the spatio-temporal dynamics of the protein-protein interaction network.

Methods

A: The virtual cytoplasm with minimum genome

206 proteins were selected following Gil et al. as a minimum set of proteins which can maintain bacterial cellular life [33]. In our model of a virtual cytoplasm, the number of copies of those 206 protein types were based on the global analysis of protein expression in yeast by Ghaemmaghami et al. [14]. Thus, our model is a theoretical construction of a possible minimal cell, without direct linkage to known species. The number of proteins used in this study is much larger than the 50 most abundant proteins [23] or the 15 selected macromolecules [22] in earlier studies.

Each protein is modeled as a rigid sphere particle. Protein molecular weight and volume (converted by average protein density 0.83 Dalton/ų) are based on the protein sequences from UniProt and calculated by Peptide Property Calculator. The isoelectric point and net charge (pH=7.0) of the proteins are estimated using the Henderson-Hasselbach equation, also based on protein sequence. The total net charge for a protein is:

$$\sum _{i=1}^{\mathit{negative}}\frac{-1}{1+{10}^{p{K}_n-pH}}+\sum _{j=1}^{\mathit{positive}}\frac{1}{1+{10}^{-\mathit{pKp}+pH}}$$ (1)

Where the pK_n is the acid dissociation constant of negatively charged amino acid, and the pK_p is the acid dissociation constant of positively charged amino acid. pKa values are critical to determine the isoelectric point and net charge at pH 7. There are several different criteria for amino acid pKa values. We chose EMBOSS.

The 70S ribosome is represented by two spherical particles, 50S and 30S, which are connected with a rigid bond. The mass of the 50S and 30S parts were taken from Table S2 of McGuffee and Elcock. The 5S RNA and 23S RNA parts of the 50S are the same mass as theirs, as well as the 16S RNA in the 30S; and the masses of the 29 L proteins in the 50S and the 20 proteins in the 30S are estimated based on their sequences. Due to the uncertainty related to the experimental ribosome effective charge, the net charges of the 50S and 30S are separately scaled by the average charge of the 206 proteins over their weights to be -50 and -25, because they were very low compared to their size.

B: Protein copy numbers in minimal proteome sets

We examine how many copies each protein should have in the minimal proteome. Protein copy number varies from cell to cell in an isogenic bacterial population, and the copy number for the low-abundance proteins fluctuates widely [18]. In addition, the 206 proteins in the theoretical minimal genome do not necessarily come from one kind of bacteria. Even for the E. coli, different experimental approaches provided totally different protein copy numbers. Ishihama and coworkers identified 1103 proteins from the cytosolic fraction of the E. coli strain MC4100, using a combination of LC-MS/MS approaches with protein and peptide fractionation steps [32]. Among the MC4100 proteins with known concentration, 164 are among the 206 proteins in the minimal proteome. Taniguchi at al., used a single molecule method and obtained the protein copy number for 1018 proteins in a single cell of E. coli strain DY330 [18], with only 92 of these matching the 206 minimal proteome set. In order to have a complete set of protein concentrations, we also searched the larger organism of yeast, for which the experimentally determined protein abundances for 6235 proteins is known [14]. Using the two E. coli sets and the single yeast set, we were able to match the 206 proteins in the minimal genome with proteins with similar functions.

Three sets of protein copy numbers for the minimal proteome were then constructed (Sup-Table 1). In the first yeast set, we assigned abundances to those 206 proteins by following the same ratios as in the experimentally observed yeast proteome [14]. For proteins without counterparts with similar biochemical functions in eukaryotes, we estimate the concentration based on the ratio from the McGuffee and Elcock work [23], or assign minimal concentration. Since we can not simulate the protein system with the actual observed copy numbers due to its large size, we scaled the copy number of the protein in the yeast by 1/2000 to simulate a proteome set of the 206 proteins. We maintain at least one copy for those proteins whose concentration is less than 2000 copies in yeast. In this way we created a ‘minimum proteome model yeast set’, totaling 4161 protein particles. Protein copy numbers in sets two and three are based on the E. coli MC4100 and E. coli DY330 experimental results [18, 32], respectively. The two experiments represent two extreme cases of ribosomal protein concentrations. The MC4100 protein concentration was dominated by 49 ribosome proteins. In the DY330 set, only ribosome protein S5 was found, probably due to the fact that protein production has to be minimized to carry the single molecule experimental characterization. In order to get balanced representations of all other proteins, we then scaled the concentration of the ribosomal proteins in the MC4100 by 1000, and the proteins in the MC4100 set with unknown copy number, were mapped from the DY330 set. The total protein particle number is also kept at 4161, with the protein concentration ratios maintained as in the MC4100 cell. Thus the MC4100 minimal proteome set was constructed. A similar procedure was followed to construct the minimal proteome set based on the DY330 cell, by mapping missing proteins from the complementary MC4100 cell. Again, the total protein particles were maintained at 4161. In the MC 4100 set and DY 330 set, if we were not able to obtain the concentration of a protein from both the MC4100 and DY300 experiments, the protein copy number was assigned to be a minimal value of one.

C: Simulations and Analysis

The interaction energies between two macromolecules are described by the Lennard-Jones potential and electrostatic interactions:

$$\mathrm{U}(\mathrm{X})={\sum _{\mathit{nonbonded}}^n\epsilon [{(\frac{R_{{\min }_{\mathit{ij}}}}{r_{\mathit{ij}}})}^{12}-(\frac{R_{{\min }_{\mathit{ij}}}}{r_{\mathit{ij}}})}^6]+\frac{q_i{q}_j}{D•r_{\mathit{ij}}}$$ (2)

where ε is the well-depth of Lennard-Jones potential, which is set to be 0.285 kcal/mol. The van der Waals radius R_i for each protein by is scaled by a factor of 1.25 of its rigid sphere radius to avoid steric overlaps between proteins. The dielectric constants D which have been tested range from 40 to 240, and the final value of 80 was used for most calculations. Due to the large size of the 70S ribosome, the non-bonding cutoff has been set to 355 Å, which is almost 3 times the radius of the 70S ribosome.

The particle movement is simulated with the Langevin dynamics:

$$M\ddot{X}=-\mathrm{\nabla }U(X)-\mathit{\gamma M}\dot{X}+\eta (t)$$ (3)

where U(X) is the interaction energy in equation 2, γ is the damping constant, and η(t) is the random force term. We used γ = 10/ps. All the Langevin dynamics simulations performed by NAMD were subjected at least 130 μs computations at 300 K with 1 ps step size, using periodic boundary conditions.

In order to validate our coarse grained model, we also carried out Langevin dynamics simulations on the system with the 50 most abundant proteins, using the proteins and the corresponding copies from Figure 1 of McGuffee and Elcock [23]. Three independent simulations were performed with different randomized initial configurations of the minimum proteome model. Finally, six random systems with different number of copies of the proteins were also investigated to compare the protein-protein interaction network with the minimal proteome model. The copies of proteins were generated randomly with at least one copy and the total individual number was kept at 4161.

Figure 1.

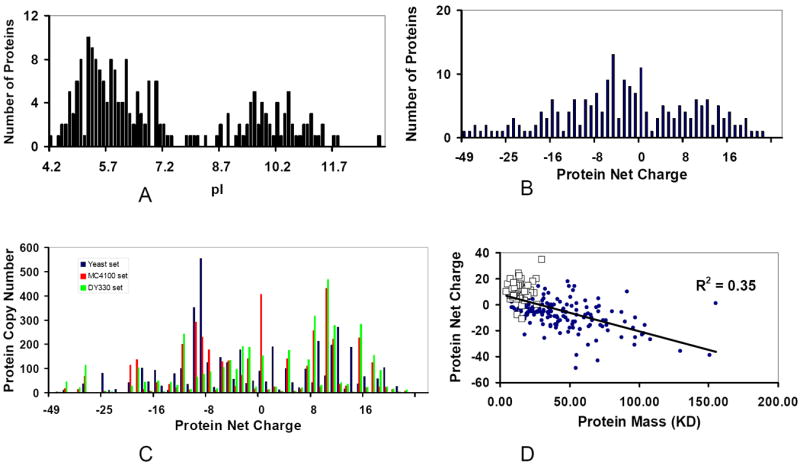
Characterization of the proteome in a minimal genome set reveals that the net charges and molecular weights for the proteins in the minimal proteome are not random. (A) Bimodal distribution of the Isoelectric point (pI) for 206 kinds of proteins agrees with other known proteomes. (B) The distribution of protein net charges for the 206 proteins. (C) The distribution of protein net charges for the 4161 protein particles used in simulation. Three sets of protein copy numbers of the minimal proteome are compared: Deep blue: yeast set; red: MC4100 set; Green: DY330 set. (D) Charge-Mass profile indicated that the net charge of a protein decreases linearly with its molecular weight. The squares are ribosomal proteins.

The length of the cubic box for the 50 most abundant protein models is 808 Å, and the lengths of the cubic box for the minimum proteome model and random models are 1090 Å. The overall specific volume for the 50 most abundant proteins and the minimal proteome model is 275 g/l. For the random models, due to the variability in protein concentration, the specific volumes of these six random systems vary from 250 g/l to 350 g/l.

The diffusion coefficients of all the macromolecules were evaluated by the Einstein equation:

$$\mathit{Diff}=\langle \mathrm{\Delta }{X}^2\rangle /6\mathrm{\Delta }t$$ (4)

where 〈ΔX²〉 is the mean square displacement and Δt is the interval. An interval of Δt = 30 ps was selected. The diffusion coefficients were the average values at 10 different periods of the simulations.

D: Clustering and intermolecular interactions analyses

Two molecules were assigned to be in a cluster and considered in contact with each other if the distance between them is under 12 Å, and all molecules in one cluster were connected with each other directly or indirectly. The clustering analysis was performed every 100 ns to investigate the interactions between macromolecules in the cytoplasm during the last 50μs simulations. According to the coordinates, the distance matrix was calculated every 100 ns and the size and the number of clusters were determined subsequently. The intermolecular contacts between unique molecules were also probed every 5 ns during the last 50 μs BD simulations.

Results

1. Characterization of the proteome in the minimal genome set

The minimal genome is an estimation of the minimal set of proteins sufficient for maintaining cellular life [33]. Here we study the properties of a minimal proteome corresponding to the minimal genome. We focus on two questions: (1) what are the abundances of the protein constituents, i.e., how many copies each protein should have; and (2) what is the charge distribution.

Based on experimental and genome conservation studies, it was estimated that a minimal bacterial genome that contains 206 protein-coding genes could provide all the functions necessary for self-maintenance and reproduction, including DNA/RNA metabolism, protein processing, and energy metabolism [31, 34]. These are listed in Sup-Table 1. The amino acid sequences of the 206 proteins were subsequently extracted from the UniProt database.

Based on the amino acid sequences of the 206 proteins, we calculated their theoretical pI values and net charges at pH 7. The distribution of these values in the minimal proteome appears to be bimodal (Figure 1A), with negatively charged proteins more populated. Such bimodal distribution is in agreement with previous observations for other proteomes [4-8]. Since now we have the protein copy numbers as well, we also examine the distributions of the protein copy number versus the protein pI values and net charges. We find that the distribution of copy numbers versus pI values similarly appears to be bimodal for all three models derived from experiments (Sup-Figure 1). However, the copy numbers of the proteins versus the protein net charges at pH 7 are not necessarily bimodal. In total, there are about thirty weakly charged (net charge -2 to 2) proteins. The distribution of the number of proteins in the minimal genome versus the net charges has two peaks around -5 and 10 (Figure 1B), and there are more protein copies with net charges around -8 and 10 (Figure 1C). But neither appears bimodal.

The protein net charge distribution in the minimal proteome is not random. The protein copy numbers in the three minimal proteome sets differ substantially; and the protein copy numbers in each individual charged state also differ (Figure 1C). However, if we examine the copy numbers in certain range, we see that there are good correlations among the three minimal proteome sets (Table 1 and Sup-Figure 1). It is interesting to note that the net charge of a protein decreases linearly with its molecular weight (Figure 1D). Most of the positively charged proteins in the minimal genome are small, with ribosomal proteins dominating (squares, Figure 1D). Large proteins tend to have large negative charges.

Table 1.

comparison of the charge distribution of three minimal proteome sets

Charge range	Protein copy number (Yeast set)	Protein copy number (MC4100 set)	Protein copy number (DY330 set)
-49, -40	5	4	5
-39, -35	11	19	47
-34, -30	3	15	21
-29, -25	122	82	128
-24, -20	67	122	40
-19, -15	275	206	214
-14, -10	577	562	399
-9, -5	975	682	424
-4, 0	414	667	657
1, 5	393	193	232
6, 10	446	840	980
11,15	711	521	645
16, 20	271	423	584
25, 35	30	27	32

Protein copy number can be defined by the specific function in a cell, which may also relate to charge and mass. In order to investigate the robustness of the protein copy number, we generated six random model sets. For each set, there are still 206 protein types and a total of 4161 protein copies, but the copy number for each protein is randomly generated. Since the protein types are the same for the native and the random sets, the distributions of the pI are still bimodal (Sup–Fig 2). However, the relative ratios of positively and negatively charged proteins are different for these model sets.

The average charges in the minimal proteome models are around -1.4 (yeast set), -0.6 (MC4100 set) and 1.1 (DY330 set), which are close to that of the complete yeast proteome (-3.6, Sup-Fig 3A). In comparison, the average charge for the 50 most redundant proteins in E. coli is highly negative (-14.4), and that from random sets varies from -0.6 to -9.4 (Sup-Fig 3). The small average charges for the minimal proteome models are consistent with the observation that smaller proteomes are more basic than larger proteomes [6, 8].

2. Calibration of the physical properties of modeled protein particles

In order to study the spatio-temporal dynamics of proteins in the minimal proteome, we simulate the minimal proteome and its random set controls. Each protein is represented as a spherical particle, with the mass being the molecular weight and the radius set to maintain a protein density of 0.83 g/ml. In all models, we added 30 ribosome particles and 8 copies of the GFP protein. The ribosome was represented by two spherical particles (one based on the mass of 30S and another based on 50S) connected by a rigid bond. The simulations were run using Langevin dynamics in a cubic box with a length of 1090 Å. Thus, the protein concentration in our simulated systems has a specific density of 275 g/l, consistent with McGuffee and Elcock’s work [23], but less than other estimation of 300-400 g/l [35].

We calibrate our simulation with published results of atomistic simulations of the 50 most abundant proteins [23] and experimental results [36]. If we compare the diffusion constants obtained for all 50 proteins, we can see that the constructed minimal proteome is more mass-dependent and agrees well with the value obtained from Brownian dynamics simulations [23] (Figure 2A). There are small differences between the protein masses used in our simulation and McGuffee and Elcock’s work [23]. We use the entire protein sequences to calculate protein mass; while McGuffee and Elcock used only the structures available either in the PDB or obtained by homology modeling, which often have missing residues. The diffusion constant for the GFP protein from our simulations is 9.31 μm²/s, which is very close to 9.1 μm²/s and 9.0±2.1 μm²/s from McGuffee and Elcock’s work [23] and in vivo experiments [36], respectively.

Figure 2.

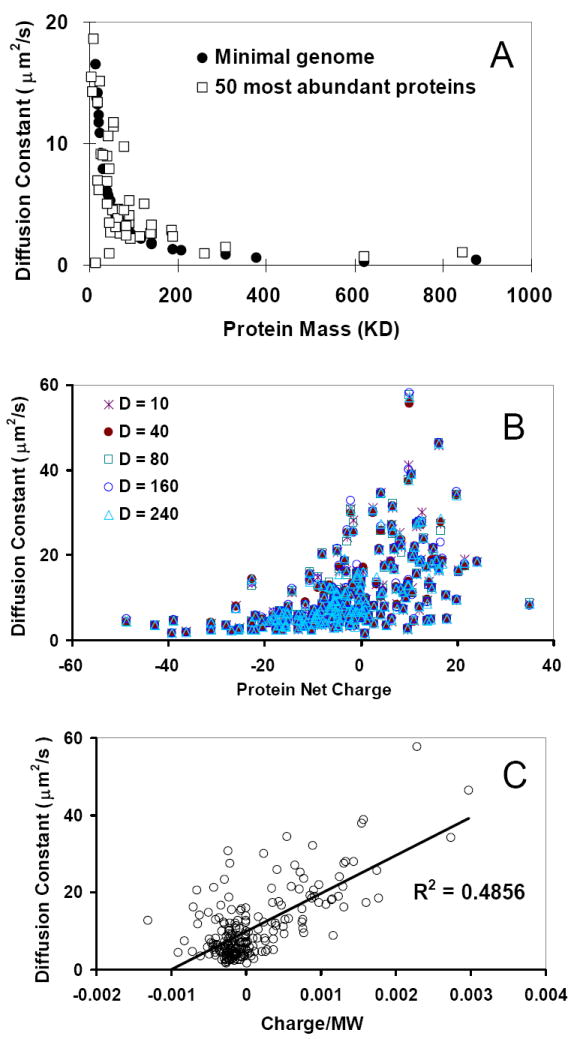
(A) Comparison of the diffusion constants obtained from the simulations (black dots) with published work for the 50 most abundant proteins (squares). (B) Diffusion constants are not dependent on the dielectric constant used in simulations. (C) Diffusion constants are correlated with the ratio of protein net-charges/mass.

Our simulations tested a range of dielectric constants. The dielectric constant in the cytoplasm could change from 50 to 200 [37, 38]. As can be seen in Figure 2B, for dielectric constants ranging from 10 to 240, the diffusion constants in our simulations change only slightly. This observation indicates that the electrostatic screen may not have a large influence on the overall diffusion behavior of the whole proteome. Thus, we used the dielectric constant of the water (80) and the friction coefficient of 10 in all simulations when no specific dielectric constant is mentioned.

Since the diffusion constant is inversely dependent on the weight of a particle, smaller proteins always have higher diffusion constant. As can be seen in Figure 1D, positively charged proteins are usually small. Therefore, they have higher diffusion constants (Figure 2B). We found that in a negatively charged environment, the diffusion constants for charged particles increase linearly with the ratio of charge and mass. As can be seen in Figure 2C, the smaller positively charged particles (higher charge/mass ratio) move quickly. As we show in the next section, the distribution of proteins with different diffusion rates, combined with their charge states, may have a profound effect on the protein-protein interaction network.

3. The spatial distribution of the protein-protein interaction network depends on the balance of charged proteins

The process of protein-protein interaction can be classified into three steps: (1) spatial clustering through diffusion/collision; (2) formation of a complex via conformational selection and population shift [39-44]; and (3) optimization of side chains and slight backbone movements via induced fit, to form the bound complex [44-46]. Here we focus on the formation of protein clusters of the minimal proteome. We analyze the collision rate of each protein and the spatial distributions of the protein clusters.

We define protein clusters to be any proteins within 12 Å from each other, a value which corresponds to about two solvation layers for each protein (Figure 3). In order to analyze the spatial distributions of the interacting proteins, all proteins within this range are merged into one cluster. The size and location of the clusters may reflect the spatial distributions of the network. We also follow the stability of the cluster by monitoring 10 snapshots in the simulation with 5 μs intervals. If a protein particle appears in the cluster in all 10 snapshots, regardless of its geometrical location, it is classified to be in that cluster (Figure 3).

Figure 3.

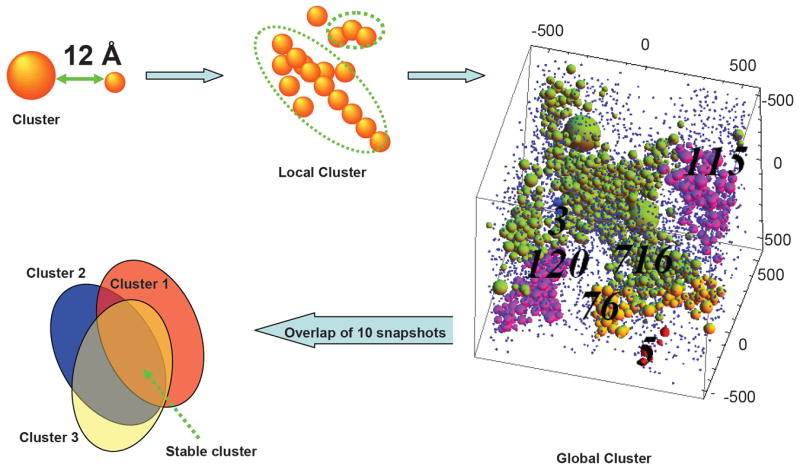
The clustering procedure used to study the spatial protein-protein interaction network. The cluster was defined to constitute of any proteins within 12 Å from each other. All proteins within this range were classified to be in one cluster which extended to the whole simulation box. In the box, the numbers (120 for the bottom purple; 76 for the orange; 716 for the green; and 115 for the top purple cluster) indicate the cluster size. The stable cluster is defined by overlapping 10 snapshots taken from the simulation, at 5 μs intervals. If a protein particle appears in the cluster in all 10 snapshots, regardless of its geometrical location, it is classified to be in the stable cluster.

After counting the number of collisions for each protein with other kinds of proteins, we found that the protein collision rate increases linearly with the absolute charge (the net positive or negative charges) of the proteins (Figure 4A). As a result, proteins with near neutral charge have the lowest collision rates. This interesting observation is the outcome of interplay between the collision cross section and diffusion speed. The sizes of negatively charged proteins are large (Figure 1D). These provide a large target collision cross-section, which leads to higher collision rates. On the other hand, the higher diffusion speed of positively charged proteins (Figures 2B and 2C) leads to frequent, and quicker movements within the crowded cellular environment, which translate into higher collision rates with other proteins.

Figure 4.

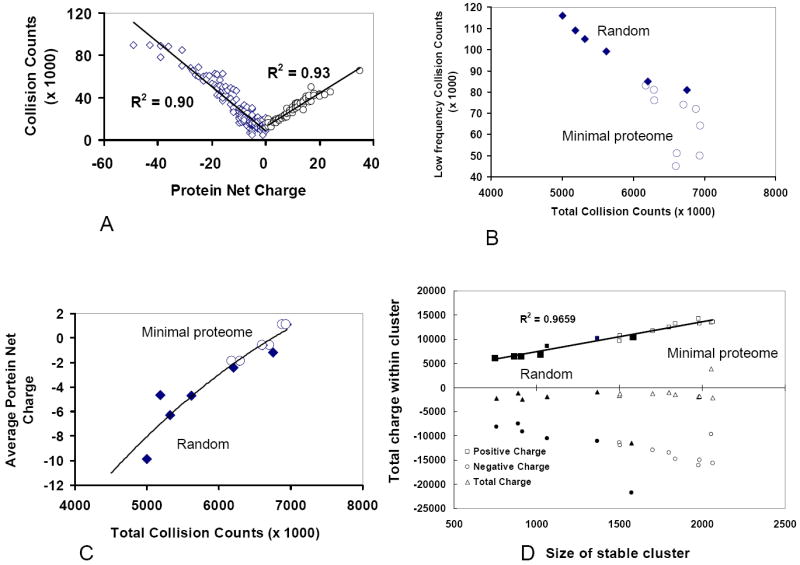
Net charge controls protein interaction network. (A) Collision rate increases linearly with the absolute charges on the proteins, i.e. it increases with the net positive and negative charges. The result from minimal proteome yeast set is shown; similar results were obtained from the simulations of MC4100 and DY330 sets. (B) The minimal proteome models have high total collision count because there are fewer proteins with low collision frequencies, which are the summation from the lowest 10 proteins. The diamonds are for the simulations of the random proteomes, and the circles represent the minimal proteome models (each with three runs). (C) The total collision counts within a proteome increase with the number of positively charge proteins. (D) The size of the stable cluster depends on the ratio between negatively and positively charged proteins with different masses. The minimal proteome models have larger stable cluster size.

We compare the collision behavior of the six random control sets with the minimal proteome model. The random sets also obey the linear relationship between the collision rate and protein charge, except for random set 4 (Sup-Fig 3B). However, comparing with the minimal proteome model, the random sets have lower collision rates (Figure 4B), except random set 3 which could be due to too many negatively charged proteins. Indeed, we found that there is a strong correlation between the total number of collisions and the average charge of the proteomes. As shown in Figure 4C, the total collision counts increase when the average protein net charges within proteomes decreases (moves toward neutrality).

The proteins in the minimal proteome model form larger clusters than the random control sets. Among clusters of different sizes, we monitor the largest cluster size along the Langevin dynamics simulation trajectories. The dominant (largest) clusters in the minimal proteome models are comprised of more than 3000 individual molecules and span the periodic simulation box, which indicates that there is an interaction network between the proteins across the cytoplasm. As shown in Figure 5, the size of this cluster fluctuates slightly over time, indicating that the cluster is dynamic. It is important to notice that three minimal proteome models (the yeast, MC4100, and DY330 sets) have similar behavior, even though the protein concentrations in the three models differ substantially. In contrast, the cluster sizes for all random sets are smaller than those of the minimal proteome models. The cluster sizes for random set 4 are close to those of the minimal proteome model. Comparisons of the stable (across time) cluster sizes of the PPI (Figure 4D), indicates that for the minimal proteome model, the stable clusters are also the largest.

Figure 5.

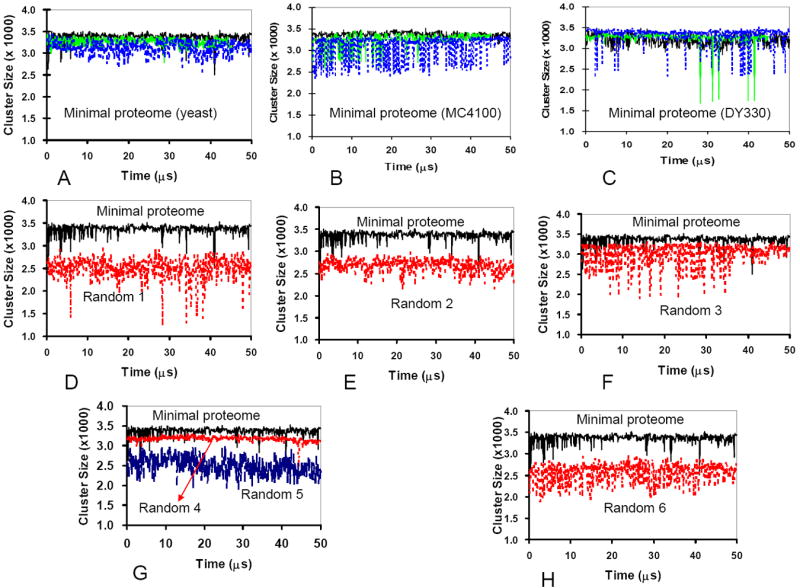
Proteomes with random populations of negatively and positively charged proteins form smaller clusters than the minimal proteome models, whose protein populations were derived from experimentally observed protein copy numbers. (A-C) The changes in the cluster size during the simulations in three independent runs of minimal proteome models. (D-H) Comparison of the cluster sizes for the minimal proteome versus random proteomes. The comparison indicates that the minimal proteome models have larger cluster sizes during the simulations.

Figure 4D also reveals that the total charges for the stable clusters are constant (dashed line), regardless of the cluster size. Random set 4 which has the most negative average charges is an exception. Essentially, the number of charged proteins controls the size of the stable cluster, with a linear increase of the size with the number of positively and negatively charged proteins in the cluster. It should be noted that it is not the overall number of positively charged proteins that controls the size of a stable cluster. This can be illustrated by counting the positively charged proteins in each set, with five of the six random sets having more positively charged proteins than the minimal proteome set (the number of positively charged proteins in the minimal proteome yeast set: 2300; in the random 1 set: 2611; random 2: 2487; random 3: 2233; random 4; 2802; random 5: 2478; random 6: 2637). However, the random sets have a stable cluster which is smaller than that formed in the minimal proteome model. Thus, the balance between the number of positively charged and negatively charged proteins in the minimal proteome model appears to influence the size of the stable protein-protein interaction cluster.

4. M. Pneumoniae has less protein-protein interactions

Mycoplasma pneumoniae is one of the smallest known self-replicating bacteria [28]. M. pneumoniae has only 690 ORFs. It is interesting to examine if the M. pneumoniae has similar protein-protein interactions properties as those we observed for the minimal proteome model.

The copy numbers of 413 proteins (59.9% of total predicted proteome) have been quantified recently [29]. Comparing these 413 proteins with the minimal proteome set, we identified 172 that have the same functions; we call these 172 proteins in M. pneumoniae the MP172 set. The correlation coefficient of the protein mass of the MP172 set with the corresponding proteins in the minimal proteome model is very high (R² = 0.74); however, the correlation of protein charge between the two sets is much lower (R² = 0.29).

Using the experimentally characterized copy numbers ratios of the MP172, we run the simulations with the same conditions as we did for the minimal proteome model (4161 protein particles, 8 GFP and 30 Ribosome). We found that the protein-protein interaction network of the MP172 is much smaller than in the minimal proteome model. As can be seen in Figure 6A, the cluster size of the MP172 set fluctuates only around 2000. The results could indicate that there are fewer protein types in the MP172 set than required to maintain a minimal proteome.

Figure 6.

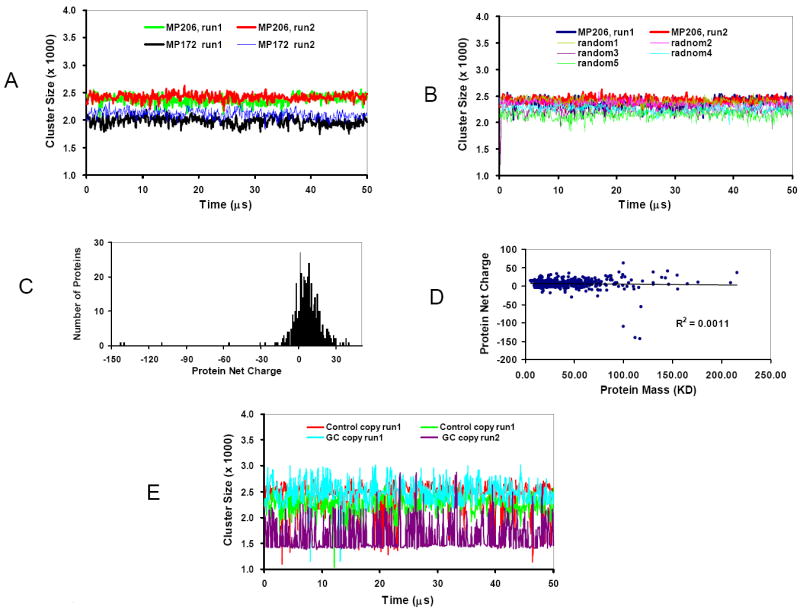
M. pneumoniae has less protein-protein interaction than E. Coli based minimal proteome. (A) The changes in the cluster size during the simulations with 172 and 206 types of proteins in the M. pneumoniae. (B) The gap between the cluster size of the MP206 set with experimental protein copy numbers and randomized protein copy numbers is small. (C) The distribution of protein net charges for the 206 proteins in the MP206 set. (D) Charge-Mass profile indicated that there is no correlation between the net charge of a protein with its molecular weight in the M. pneumoniae proteome. (E) The cluster size obtained in the simulations of 206 proteins using the charge and mass of E. coli proteins, but with the protein copy numbers obtained from M. pneumoniae proteome.

To check these results, using less strictly matching criteria we expand the MP172 set to 206 kinds of proteins, the same number as in the minimal proteome. We call these 206 proteins in the M. pneumoniae the MP206 set. The correlation between the MP206 set and minimal proteome model decreased (R² = 0.59 and 0.12 for protein mass and charge, respectively). However, the subsequent simulation indicated that the MP206 set has a larger protein-protein interaction network than the MP172 set, but still smaller than that of the minimal proteome model (Figure 6A). Further simulations with all 413 proteins with known copy numbers in the M. pneumoniae (the MP413 set) reveal that the protein-protein interaction cluster size in the MP413 set is similar to that of MP206 set. These results confirmed that a minimal number of protein types in a proteome are required to maintain efficient protein-protein interactions.

We examined the effects of randomized protein copy numbers in the MP206 set. Five random sets were generated and simulated. As can be seen in Figure 6B, while the MP206 still has the largest cluster, the gaps between the random sets and the experimentally observed MP206 set are marginal. Similar results were obtained using all 413 proteins.

Unlike the proteomes of E. coli and higher organism of yeast, the proteome of M. pneumoniae is highly positively charged (Figure 6C), and there is no correlation between protein mass and charge (Figure 6D). The uncoupling of protein mass and charge in the M. pneumoniae proteome could be responsible for the smaller protein-protein interaction cluster. To check this possibility, we run the simulations of 206 proteins using the charge and mass of E. coli proteins, but with the protein copy numbers obtained from M. pneumoniae proteome. Interestingly, we found that the protein-protein interaction cluster using the combinations of E. coli proteins and M. pneumoniae copies are not stable. As shown in Figure 6E, the cluster sizes observed during the simulations fluctuate from 1500 to 3000, which is the range observed in random simulations for the minimal proteome model (Figure 5).

The above simulation results are consistent with the experimental characterizations of the M. pneumonia network [47, 48]. While there is little difference between the M. pneumoniae, E. coli, and yeast for individual protein-protein interactions [48], the network in M. pneumoniae is less interconnected [47]. Consistently, we have shown that the M. pneumoniae cluster size is smaller than that in the minimal proteome model, which is based on E. coli proteins. The smaller gap between the cluster sizes of the random sets and MP206 (and MP413) indicates that the protein-protein interactions networks in the M. pneumoniae could be less organized than in more complex organism.

Discussion

Understanding the behavior of fundamental cellular processes is important. Various experimental and computational methods have been used to study the dynamic locations of proteins in the cell to understand protein functions and network complexity [13, 49]. Signals enter the cell via some perturbation event taking place on the extracellular domain of a receptor; or via diffusion of small molecules through the cytoplasm. Signaling propagates through dynamic conformational changes and population shift of the network which takes place through direct protein-protein interactions. Eventually, these lead to cellular response, often by turning on/off genes. Efficient signaling and metabolic responses are critical for cellular health. To prevent delays which may occur if proteins and metabolites would diffuse in the cell, the protein network is spatially organized, such that proteins fulfilling similar functions are near each other.

To study large scale protein-protein interactions, here we represent protein molecules as charged spherical particles. The simplification allows us to investigate the dynamic behavior of a complete proteome of a minimal genome. Proteins are not spherical; and their dimensions could change upon interaction, as in intrinsically disordered proteins [43, 50, 51]. Further, the charges are not homogeneously distributed across the molecular surface. Estimation of net protein charges is also challenging [52], and dual-targeted proteins can have different net charge at different locations [53, 54]. Solvation effects also change protein electrostatic interactions [55]. Moreover, crowding was shown to modulate the kinetics of diffusion-limited processes, and can increase the association rate several fold, with a non-monotonic trend of the rate as a function of the bulk density of the particles [56, 57]. In addition, simulation times are always shorter than biological time scales. Nevertheless, using our representation of protein charge and mass distribution, our simulations revealed several fundamental features governing protein-protein interactions on the proteomic scale.

First, our study enhanced and extended the previous minimal genome compilations [31, 34] by assigning protein sequences and copy numbers to all 206 proteins in the minimal genome, leading to a complete workable model. We found that net charges and molecular weights for the proteins in the minimal genome are not random. The net charge of a protein decreases linearly with its molecular weight, with small proteins mostly positively charged and large proteins negatively charged. The diffusion constants for charged protein particles increase linearly with the ratio of charge and protein mass.

Secondly, we found that the protein copy numbers in the minimal genome have the tendency to maximize the size of the protein network. Our models are theoretical construction of essential proteins for a possible minimal cell. The assignment of protein copy number to the theoretical minimal proteome introduced certain inevitable distortion of intrinsic ratio of protein copy numbers, mainly due to two sources. First, there is no complete experimentally characterized protein copy number for an E. coli proteome. The combination of protein copy number from different experimental approaches and E. coli strains may have some inconsistencies. Second, to be able to carry out simulation, we have to reduce the real protein copy number to a practical level. Proteins with low concentrations may have large ratio change due to the copy number reduction. For example, the experimental copy numbers of ycfF and ycfH show a 10-fold difference, whereas in the MC4100 dataset used for simulation, the difference is only 4-fold. Nonetheless, these changes of the intrinsic ratio of several individual proteins do not distort the overall charge distributions in the minimal proteome. As can be seen in Table 1 and Supplementary Material Figure 1, the protein numbers in similar charge distribution regions are correlated, even though the actual protein numbers from different experimental datasets differ due to either experimental observation or our dataset scaling. Furthermore, we found that the protein copy number ratios have certain fluctuation tolerance, since all three datasets sets of protein copy numbers derived from different experiments converged to similar simulation results, which are different from those of randomly generated protein copy numbers. The tolerance of protein number fluctuations is probably due to the pressure to accommodate protein concentration change during cellular life cycle.

Our study revealed the importance of the relative populations of negatively and positively charged proteins in a proteome. Negatively charged proteins have large sizes and can provide large collision cross-sections which facilitate interaction with other proteins; and positively charged proteins have high diffusion speed and higher collision frequencies with other proteins. Thus, with proper ratio, negatively and positively charged proteins can form stable clusters spanning large area. Proteomes with random populations of negatively charged and positively charged proteins form less stable clusters than those with protein populations derived from experimentally observed protein copy numbers. Using E. coli proteins as the model for the protein charge and mass in a minimal proteome model, it is interesting to see that protein concentration mapped from yeast provided a better framework for protein-protein interactions than that mapped from M. pneumoniae, which is among the smallest organisms. There are two reasons that might account for the outcome. Firstly, the compilation of minimal proteome was based on selection from many organisms. As a result, it is easy to map the correct protein concentration from a larger organism than from a smaller organism, which cannot match all protein in the theoretical minimal proteome. Second, both yeast and E. coli are much more complex than M. pneumoniae. While both these proteomes are negatively charged, the M. pneumoniae proteome is positively charged.

Proteins are clustered within inter-connected regions based on their physical properties such as charge, mass, size, geometry, topology and stability which have been optimized by evolution. Within a proteome, each protein has a unique characteristic ratio of net charge versus molecular mass which fit its functions in the cell. A study of human serum immunoglobulin along a pH gradient of ampholytes indicated that each isotype displays a specific pI range, with limited overlap [58], indicating the importance of net charge for finding the interacting partner within the local environment [59]. It has been observed that charge and size drive spontaneous self-assembly of oppositely charged globular proteins into microspheres [60], which may correspond to local arrangements of different proteins within a cell. Proteins typically cluster to perform their functions, for example, by forming transcriptional factories [9], or the assemblies of the general transcription factors and RNA polymerase II on promoters for transcription initiation/activation [61]. Therefore, the arrangement of proteins with different charges and sizes can be important for functional efficiency. In addition to the local organization, our observation of large stable clusters may also suggest how cells can maximize productive encounters. Nonspecific protein-protein interaction could limit the number of proteins in a cell [62]. Living cells need to form functional protein complexes while minimizing promiscuous nonspecific interactions [63]; this is important in metabolic and signaling pathways. Therefore, clustering at given sites in the cell would increase functional (and decrease non-functional) interactions.

Our study demonstrates the critical roles of positively charged proteins in maintaining the network. It has been found that small proteomes often have more positively charged proteins [6, 8]; an observation which is consistent with our finding of the fundamental roles of positively charged proteins. Many positively charged proteins are ribosomal or DNA-binding proteins, with clear biological functions; one example is the interactions between positively charged proteins and DNA phosphate backbones which are involved in a four-way Holliday DNA junction, an intermediate in homologous recombination and a central component in DNA recombination and repair [64]. However, proteins with extremely alkaline pI are often very poorly represented using traditional proteome technology [65-67], and the functions of positively charged proteins still need to be investigated. Ribosomal proteins are such examples. In addition to their roles in ribosome assembly, they also have important functions in cell signaling [68]. Analysis of the essential core of protein-protein interaction networks in E. coli also found that ribosomal proteins have additional important functional roles [69].

The requirement to maintain proper concentration of positively charged proteins in the cytoplasm can also be illustrated by the highly abundant lysozyme in egg-white. Lysozyme constitutes about 3.4% of the egg white proteins, and it is unusual among the major egg white proteins in being highly basic (pI =10.7) [70]. Lysozyme may also have an anti-bacterial role [70, 71] important for cell defense. Lysozyme is one of the smallest major egg white proteins. It is possible that lysozyme helps to maintain the architecture of protein-protein interaction network in egg-white, for example by forming complexes with ovomucin, ovalbumin and ovotransferrin [70].

The concept of the minimal genome provides insight into a fundamental genomic requirement to maintain cellular life. Our construction of the corresponding proteome which is based on the minimal genome allows direct simulation of the virtual minimal cell. Our observation that the minimal genome model has the highest number of interacting proteins reveals nature’s requirement: to fulfill its native function, a protein should maintain a certain combination of charge/mass/concentration. It is interesting to note that the minimal genome model based on the charge and mass of E. coli could have more extensive protein-protein interaction network than that based on the lower organism M. pneumoniae.