Figure 2.

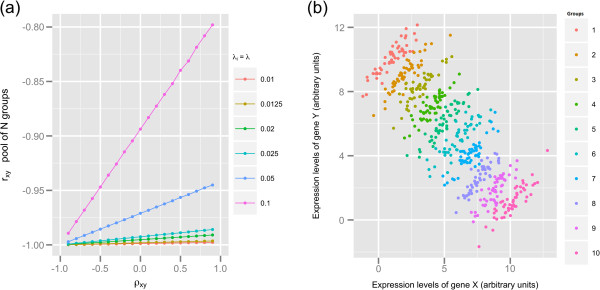
Mean differences across a pool of N groups causes Simpson’s paradox. (a)r_xy was obtained from combining N groups of simulated data; simulation parameter ρ_xy is the true correlation of the pair xy within each group i = 1,N for . All other simulation parameters are as follows: μ_xy,i = (i,N−(i−1)), −0.9 ≤ ρ_xy ≤ 0.9, n_i = 10, λ_i = λ, 0.01 ≤ λ ≤ 0.1, for i = 1,N, and 10 ≤ N ≤ 100. (b) Scatterplot of a pair xy obtained with the simulation parameters: μ_xy,i = (i,(11−i)), ρ_xy = 0.9 and n_i = 50 for i = 1,10 groups. This plot shows clearly that even though there is a positive trend within each of the 10 groups, the trend across the pool of 10 groups is negative (Simpson’s paradox).