Fig. 2.

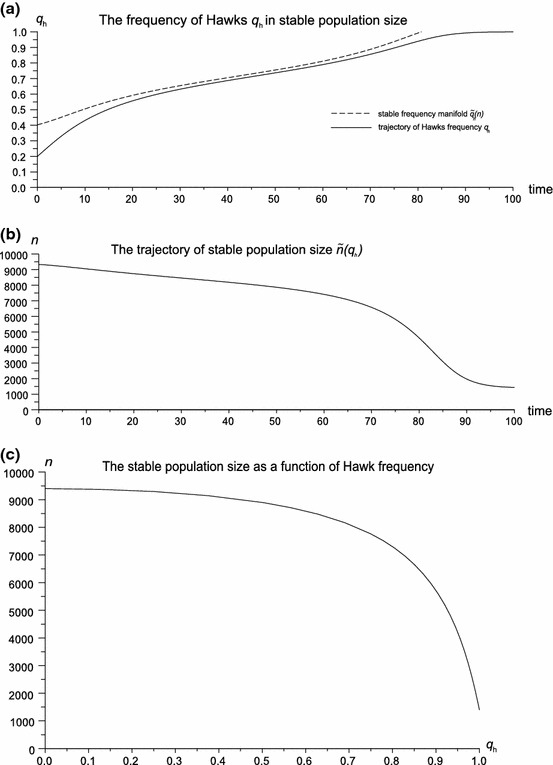
The stable population size is a dynamic equilibrium between mortality and fecundity. An increase of mortality caused by the spreading of Hawks can reduce the population size, even to extinction. a A plot of strategy frequencies. The attractor manifold \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\tilde{q}_{h}(n)$$\end{document} exceeds 1, causing the extinction of Doves. b The corresponding trajectory of the population size. c The stable population size as a function of Hawk frequency. Parameter values are \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$W=10,W_{b}=0,d=0.8,b=0.7$$\end{document}. In this case there are no mixed equilibria, Hawks outcompete Doves and the population size converges to \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\tilde{n}=1{,}400$$\end{document}