Computational Methods of Studying the Binding of Toxins From Venomous Animals to Biological Ion Channels: Theory and Applications

Abstract

The discovery of new drugs that selectively block or modulate ion channels has great potential to provide new treatments for a host of conditions. One promising avenue revolves around modifying or mimicking certain naturally occurring ion channel modulator toxins. This strategy appears to offer the prospect of designing drugs that are both potent and specific. The use of computational modeling is crucial to this endeavor, as it has the potential to provide lower cost alternatives for exploring the effects of new compounds on ion channels. In addition, computational modeling can provide structural information and theoretical understanding that is not easily derivable from experimental results. In this review, we look at the theory and computational methods that are applicable to the study of ion channel modulators. The first section provides an introduction to various theoretical concepts, including force-fields and the statistical mechanics of binding. We then look at various computational techniques available to the researcher, including molecular dynamics, Brownian dynamics, and molecular docking systems. The latter section of the review explores applications of these techniques, concentrating on pore blocker and gating modifier toxins of potassium and sodium channels. After first discussing the structural features of these channels, and their modes of block, we provide an in-depth review of past computational work that has been carried out. Finally, we discuss prospects for future developments in the field.

I. INTRODUCTION

Ion channels are ubiquitous in the human body. When a particular channel is over- or underexpressed, or contains a mutation which changes its conduction or gating characteristics, disease may result (12). There are many such channelopathies, including type I diabetes, epilepsy, cystic fibrosis, multiple sclerosis, long-QT syndrome, and migraines. Treatment of these diseases can be effected by introducing ion channel modulator drugs that regulate the function of the channels. For example, Ziconotide, the synthetic form of the ω-conotoxin MVIIA, which is a voltage-gated calcium channel blocker, has been approved to treat severe pain (216). These modulators may be agonists, which increase the conductance of the channels, or inhibitors, which reduce their conductance. Channel blockers are inhibitors that operate directly, by binding in the ion conducting pore. The block may be extracellular, as is the case for pore blocker toxins, or intracellular, for example, internal block of potassium channels by tetraethylammonium. Modulation may also be accomplished indirectly, by affecting the activation or inactivation gating of the channel. For example, the gating modifier hanatoxin binds to the voltage sensor of voltage-gated potassium channels and moves the activation curve of the channel to the right, thus requiring a greater depolarization to open the channel. Quinidine, on the other hand, is proposed to bind to the intracellular face of the Kv1.4 channel and allosterically promote the onset of C-type inactivation (243). Batrachotoxin has been proposed to bind in the pore of voltage-gated sodium channels (246) but does not block the flow of ions; instead, it locks the channel in a permanently open conformation. Thus there are a variety of modes by which channel modulators may function.

Nature has devised a plethora of ion channel blockers and modulators, in the form of toxins that occur in the venoms of poisonous creatures such as scorpions, cone snails, sea anemones, spiders, and snakes. We have already mentioned two gating modifier toxins: hanatoxin and batrachotoxin. Many other toxins act by directly blocking the pore, usually by inserting a basic lysine or arginine side chain into the selectivity filter from the extracellular side. These toxins tend to be extremely potent. Often, they are relatively unselective, affecting several members of a whole family of ion channels. However, some are known to discriminate extremely well between similar members of an ion channel family; for example, modified sea anemone ShK channels bind to Kv1.3 voltage-gated potassium channels with at least 100-fold selectivity over other Kv channels. This kind of selectivity, along with the general structural complexity of these toxins, gives hope that they may be used as a starting point to develop potent and selective drugs. Such toxins form a particular focus of this review, although much of the theoretical discussion in the earlier parts of the review applies more generally.

A great deal of effort goes into the study and development of ion channel modulator drugs, due to the range of conditions which may be treated and the promising possibilities for treatment. To be potent, such drugs should bind strongly to their receptors. To avoid unwanted side effects, they should not bind to antitargets. Finally, when bound to receptors, they should bring about the desired effect, for example, by actually blocking or inhibiting current through the channel. Drug development is a costly and time-consuming process. Typically, thousands of compounds are initially screened. The most promising leads are then modified, and various stages of further characterization and testing are carried out. State-of-the-art experimental technology automates many of the tasks involved in testing new compounds (73), but despite the high cost and sophistication of the techniques, only crude clues about the mechanisms of modulation or block may be gained.

These limitations have given rise to an intense interest in the use of computational modeling as a complementary means to investigate the binding modes, binding affinities, and modulation mechanisms of channel modulators. Ideally, one would like to study the effects of channel modulators on channel function, using a model assembly composed of an ion channel embedded in a lipid bilayer, ions, and water molecules. Computational modeling can in principle reproduce many or all the experimental observables, such as the binding affinity and specificity of a given modulator on various subfamilies of ion channels. Additionally, and perhaps more importantly, modeling has the potential to reveal in exquisite detail the interactions, mechanisms, and structural contacts involved in modulator binding. This is important because such information is not easily deduced from electrophysiological experiments. Currently, no single available computational method is able to achieve all these idealized aims. There are, however, a number of computational techniques that can perform some of these tasks with varying degrees of efficiency. Each of these methodologies has advantages and disadvantages. At various points in the drug development cycle, it is necessary to make compromises between computational speed and accuracy. For example, lead discovery typically requires a very fast, less accurate assessment of binding affinity, since thousands of potential lead compounds may need to be screened. The techniques discussed in this review can be ranked according to whether they are crude but fast, or slow but accurate. Different techniques will be appropriate at different points in the drug development cycle. The aim of devising a technique that is both fast and accurate remains the holy grail of the field.

In this review, we will discuss three commonly used techniques: molecular dynamics, Brownian dynamics, and docking. Molecular dynamics simulates all or many of the atoms in the system using a classical force field. Brownian dynamics is similar, but always uses implicit water, and makes extensive use of rigid and fixed molecules to achieve greater speed. Docking employs various algorithmic search strategies, and scoring functions to attempt to predict the binding modes between a ligand and a receptor and to estimate the binding affinity. A fourth approach, QSAR, makes use of multidimensional regression on various properties of drugs and targets. Although we consider QSAR to be somewhat outside the scope of this review, we mention it due to its importance and potential usefulness as a tool for drug discovery.

We will begin the review by detailing the computational techniques listed above: molecular dynamics, Brownian dynamics, and docking. We will then go into more theoretical detail about the tasks that computational modeling and simulation can help to solve. Binding affinity is a key determinant of modulator effectiveness. For example, if a channel blocker always fully blocks the channel upon binding, then binding affinity will be directly related to the degree of block. We shall consider the theoretical basis of binding affinity and relate it to the free energy of binding for the blocker. Although calculating the free energy of binding is far easier than directly calculating binding affinity from simulations, it is nonetheless a formidable computational task. Therefore, having laid the theoretical groundwork, we will consider some of the techniques that have been devised to calculate free energies of binding. We will next look at specific computational studies of interactions between ion channels and their modulators. Starting with an overview of ion channel diseases and pharmacology, and aspects of ion channel structure, we will go on to review examples of computational studies involving different mechanisms of block, namely, pore block in potassium and sodium channels and gating modifiers in these channels. Finally, we will conclude the review with a discussion of future prospects for computational modeling. Due to the difficulty of the problems faced, it is clear that much important theoretical and computational work still lies ahead, and hence, we predict important and revolutionary developments in the future.

A. Scope of This Review

The subject of ion channel modulators is broad, and the literature is large. Computational studies of ion channel block may employ a raft of techniques from physics, chemistry, biology, bioinformatics, and computer science. Due to the size and complexity of the subject, we have chosen to concentrate on certain topics at the expense of others. The reader should, however, be aware that there are other interesting computational techniques that may be applicable, from the realms of statistics, bioinformatics, and machine-learning. We touch on some of these techniques in passing: for example, QSAR and knowledge-based potentials rely on bioinformatics, and certain docking force fields, for example, AUTODOCK VINA, have only a loose connection to physical principles, relying instead on machine learning approaches to parametrization.

In the latter sections of the review, where we look at specific computational studies of ion channel block, we have not attempted to cover the full range of channels and modulators. Instead, we concentrate mainly on toxin-derived pore blockers and gating modifiers of potassium and sodium channels. Potassium and sodium channels were chosen due to their importance and widespread occurrence in all manner of tissues, for example, they are primarily responsible for all nerve and muscle impulses, and because they are implicated in a large number of channelopathies. Our focus on toxins is due to their prominence in current research effort and the hope they appear to offer for developing new drugs that will selectively target individual types of channels.

II. COMPUTATIONAL MODELS AND METHODS

A. Ion-Channel Specific Issues

Much of the theory of ion-channel modulators deals with the generalities of protein-protein or protein-ligand binding. However, ion channels do exhibit several peculiarities that may need special consideration, and which the reader should keep in mind.

The pores of ion channels focus electric fields, due to the geometry of the dielectric boundary (135). One effect of this is to increase the interaction between resident ions in the channel, and blockers that enter the pore. For example, Park and Miller (185) found that a modest but significant interaction of around 3 kT¹ exists between the Lys27 residue in charybdotoxin and resident ions in the pore; this would correspond to a factor of 20 in the binding affinity. Tetraethylammonium block in potassium channels is also known to depend on ionic concentration (134). Another related effect of the dielectric boundary of ion channels is that they exhibit a sharp voltage drop through the pore due to the membrane potential, particularly across the selectivity filter. The membrane potential can thus affect the binding of blockers. The most notable examples of this are for small ionic molecules such as tetraethylammonium that bind in the internal vestibules of ion channels. Positively charged tetraethylammonium was found to have a binding affinity to KcsA that increased with membrane depolarization (108, 134), which is simply explained by the fact that a negative membrane potential creates a potential hill for the molecule as it moves upward into the pore, towards its binding site. Polypeptide toxins are also known to have voltage-dependent affinities (72, 83). Because the electric fields found in ion channel pores are large, a careful computational treatment is needed if errors are to be avoided.

Another complication arises from the fact that ion channels are membrane proteins. The presence of the lipid bilayer modifies the electrostatic environment. More importantly, certain toxins, such as the gating modifier hanatoxin, act from within the bilayer (221) in a complex manner, complicating computational modeling (17, 109, 153, 154, 179, 251).

The pores of ion channels also provide a more fully enclosed receptor environment than is usual in docking studies; thus care needs to be taken in making sure that the conformation of the pore allows the blocker to correctly bind. In practice, this means that either a fully flexible treatment of the channel may need to be employed, that a careful choice needs to be made for the conformation of the channel model, or that an ensemble of channel models might need to be employed (144, 161, 198, 199).

Ion channels undergo significant conformational changes that are associated with (in)activation and gating. The binding of many blocker molecules depends on the state or conformation of the channel. For example, many small-molecule local anaesthetic blockers of sodium channels exhibit state-dependent block (67). This may also manifest as a use-dependent block, where blocking efficiency is enhanced when channels cycle more frequently between closed, open, and inactivated states. Another example concerns the apparent state-dependent binding of small-molecule blockers in the inner cavity of Kv11.1/hERG channel (189). State dependence of channel block presents an additional complication that may need to be taken into account when carrying out computational work.

In the following section, we shall discuss the main computational methods used in the study of ion channel modulators: molecular dynamics, Brownian dynamics, and docking. Each of these computational methods employs one or more force fields in combination with a simulation or docking protocol. Because the force fields are to some degree interchangeable between the computational methods, for example, molecular mechanics force fields are deployed in both molecular dynamics simulations as well as certain docking systems, we shall begin the section with a look at force fields, and then move on to consider the four computational methods themselves.

B. Forces and Force Fields

In the study of biomolecules, force fields can be roughly ranked according to the degree of approximation and coarse graining that is applied. Thus, at the lowest level, we have quantum mechanical force field protocols, as used in ab initio molecular dynamics. At increasing levels of abstraction are the fully atomistic classical molecular mechanics force fields, united atom molecular mechanics force fields, implicit solvent force fields, and various types of coarse grained force fields, such as the so-called “knowledge-based” PMFs. Since quantum calculations are too slow to be practical for most questions directly relevant to modulators and ion channels, we shall begin by looking at classical molecular mechanics.

1. Atomistic molecular mechanics

In fully atomistic molecular mechanics, there are three types of potentials to consider: the electrostatic potential describing the Coulomb forces in the system, van der Waals terms describing the nonpolar interactions between pairs of atoms, and covalent, or strain, potentials describing the effects of covalent bonds between the atoms in the simulation.

Electrostatic Coulomb potentials act between pairs of atoms and contribute to the internal and interaction energies of the channel and the channel modulator. The potential between two charges q₁ and q₂ separated by a distance r in a vacuum is

$$U\left(r\right)=\frac{1}{4\pi {\epsilon }_0}\frac{q_1{q}_2}{r}$$ (1)

where ε₀ is the permittivity of free space. Coulomb potentials act at both long and short ranges and play a direct role in binding. The long range part of the Coulomb potential can attract charged blockers into oppositely charged vestibules of ion channels, and the short range part causes charged groups to form salt bridges or hydrogen bonds, locking the blocker into place in the binding pocket.

van der Waals potentials are short range potentials that describe both short range repulsive steric forces between atoms as well as longer range attractive dispersive interactions. They are usually modeled using the Lennard-Jones (6–12) potential

$$U\left(r\right)=ϵ\left\{{\left(\frac{r_{\min }}{r}\right)}^{12}-2{\left(\frac{r_{\min }}{r}\right)}^6\right\}$$ (2)

where r is the distance between two atoms, ϵ is the depth of the attractive well, and r_min is the separation between two atoms for minimum potential energy. van der Waals potentials play a role in binding by balancing attractive Coulomb interactions (thereby regulating hydrogen bonding) and in the forces that arise when the surface of the modulator contacts the channel, such as the hydrophobic force.

Covalent, or strain, potentials describe the resistance of a molecule to deformations of the relative positions of the atoms relative to one another. The actual many-body force field is complicated and depends on the quantum chemistry of the molecule. Classical molecular mechanics force fields employ a simplified treatment that considers forces between bonded pairs, triplets, and quadruplets of atoms, along with cross-term corrections. The precise implementation of these terms will vary depending on which molecular dynamics force field is chosen. Here, as a typical example, we give details of the covalent potentials in the CHARMM force field (156). Covalent bonds are first defined for the molecule, as per the “ball and stick” models used in chemistry. Five kinds of covalent potentials are then assigned to the bond network.

1) Bond stretching potentials act between pairs of neighboring atoms and take the form

$$V_{\text{bond}}=k_b{\left(b-b_0\right)}^2$$ (3)

where k_b is twice the harmonic spring constant, b is the distance between the atoms, and b₀ is the equilibrium bond distance.

2) Angle bending potentials act between adjacent triplets of atoms and take the form

$$V_{\text{angle}}=k_{\theta }{\left(\theta -{\theta }_0\right)}^2$$ (4)

where k_θ is again twice the spring constant, θ is the angle subtended by the adjacent bonds, and θ₀ is the equilibrium angle.

3) Dihedral potentials act between groups of four linearly connected atoms, and take the form

$$V_{\text{dihed}}=k_{n,\varphi }\left[1+\cos \left(n\varphi -\delta \right)\right]$$ (5)

The dihedral angle ϕ represents a torsion around the B-C bond in the group A-B-C-D as the angle formed between the planes defined by triangles A-B-C and B-C-D. k_n,ϕ gives the strength of the potential, n gives its periodicity, and δ controls the angle at which the minimum potential occurs.

4) Improper dihedral potentials are defined for groups of four atoms consisting of a central atom C to which is connected three other atoms A, B, and D. They are used primarily to maintain planarity for the group, and take the form

$$V_{\text{improp}}=k_{\omega }{\left(\omega -{\omega }_0\right)}^2$$ (6)

where k_ω is twice the spring constant; ω is the angle between the plane containing atoms A, B, and C and that containing B, C, and D; and ω₀ is the equilibrium angle.

5) Urey-Bradley potentials represent an additional way of maintaining angles: they are simply a bond potential that is defined between atoms A and C in a connected group A-B-C.

Cross terms, such as the CHARMM CMAP backbone correction (157), may also be defined to represent, for example, the interaction between adjacent dihedrals in the protein backbone.

2. Implicit solvent force fields

Water molecules account for a large proportion of atoms in biomolecular systems. By treating water molecules as a continuum, we are able to gain computational speed at the cost of accuracy. Implicit solvent force fields are used in both implicit solvent molecular mechanics and other techniques such as Brownian dynamics and various docking protocols. Below, we will give some background to the physical role played by water, and outline the techniques used for treating it implicitly as a mean field. Water has two important physical effects on biomolecular systems. First, it strongly modifies the electrostatic forces experienced by the ions and biomolecules, and second, it gives rise to short-range nonpolar forces due to van der Waals interactions and entropic effects. We shall consider these two effects in turn.

The most important effect of water, when considered as a mean-field, is that it approximates a linear dielectric medium with a high dielectric constant. This means that when two charges are surrounded by water, the Coulomb potential, given in Equation 1, will be modified so that ε₀ → ε_rε₀, where ε_r is the relative dielectric constant of water, approximately equal to 80. Coulomb forces are therefore reduced by a factor of 80. Furthermore, when water surrounds a low dielectric protein or lipid environment, a dielectric barrier is created between the water and the low dielectric region. Charges in the water are repelled from this barrier due to image forces. Other more complicated interactions involving two or more charges can also occur, especially in the pores of ion channels, where the narrow aqueous pore is completely surrounded by the protein. The physics of these effects is described by the Poisson-Boltzmann equation

$$\nabla ·\left[\epsilon \left(r\right)\nabla \varphi \left(r\right)\right]=-{\rho }_f\left(r\right)-\lambda \left(r\right){\displaystyle \sum _i{\rho }_i^0\exp \left(-\frac{{\rho }_i^0\varphi \left(r\right)}{kT}\right)}$$ (7)

In this equation, ρ_f is the solute charge distribution (i.e., the fixed charges in the ion channel and channel modulator), i represents the different ion species in the solution (e.g., Na⁺ and Cl⁻), and ρ_i⁰ are their number densities in uniform solution that is far from the channel. The term in the exponential scales these densities by their Boltzmann factor. Note that the presence of ϕ in this term makes the equation nonlinear. λ is a position-dependent scaling factor that represents the accessibility of different regions to ions, for example, ions will not physically be able to penetrate the interior of the channel protein, and thus λ would be zero in this region. The equation may be linearized to more easily solve it.

In the Poisson-Boltzmann equation, the mobile ions in the system are treated as a mean field. This approach has been shown to have limitations when dealing with the narrow pores that are often present in ion channels (173). Therefore, it is often preferable to model the ions explicitly, by treating them as part of p_f in the above equation, and setting the mean-field ion densities to zero. We then have Poisson's equation

$$\nabla ·\left[\epsilon \left(r\right)\nabla \varphi \left(r\right)\right]=-{\rho }_f\left(r\right)$$ (8)

which is a linear partial differential equation.

Since direct solutions of both the Poisson-Boltzmann and Poisson's equation are time consuming, approximations are often used. The simplest approximations use Coulomb potentials between charges, with a distance-dependent dielectric such as ε(r) = 4r (111). The dielectric constant increases linearly with increasing r, which represents the fact that, for greater r, there is likely to be more solvent between and around the charges. However, details of the geometry are not taken into account.

A more sophisticated method is the generalized Born approach (15). Generalized Born electrostatics represents the free energy of the polarization of the solvent as

$$F=\frac{1}{8\pi }\left(\frac{1}{{\epsilon }_0}-\frac{1}{\epsilon }\right){\displaystyle \sum _{i,j=1}^N\frac{q_i{q}_j}{\sqrt{r_{ij}^2+a_{ij}^2\exp \left(-r_{ij}^2/4a_i{a}_j\right)}}}$$ (9)

where q_i is the atomic partial charges of the ith atom, r_ij is the distance between atoms i and j, and a_i is a parameter known as the generalized Born radius of atom i. There are various methods of computing the generalized Born radii, and their optimal determination lies at the heart of the method. The precise form of Equation 9 is to some extent arbitrary, but is required to give the correct result for certain limits. For large r_ij, the method gives the Coulomb force for two point charges in a dielectric medium. As the interatomic distance decreases, additional solvent screening and image charge effects become manifest. For a single atom, with a_ij set to the atomic radius, the method gives the analytical Born solvation energy. The correct expression is also obtained for the limit of a point dipole.

The electrostatics inside the pore of ion channels present extra challenges, due to the presence of highly focused electric fields, and other problems with the mean-field approximation due to the quantization of water and ions in narrow pores. This may be important to the study of channel-blocker interactions, including those where binding involves the insertion of a blocker lysine or arginine into the channel pore. For example, tetrodotoxin is known to block voltage-gated sodium channels in a voltage-dependent manner (72, 83), suggesting that the pore electrostatics play a large role in the block. Because of the electrostatic focusing effect, the pores of ion channels increase the strength and range of charge-charge interactions in a position-dependent manner. Another way of looking at this is that there is less surrounding water to shield charges from one another. Furthermore, the membrane voltage drop occurs almost entirely over the length of the channel pore and is greatest where the pore is narrow. It is possible that general purpose docking programs and the like, which may be optimized for the docking of a ligand or protein onto a receptor located on the surface of another protein, may not perform well under the highly enclosed conditions of ion channel pores. However, very little work has been done to quantify these issues.

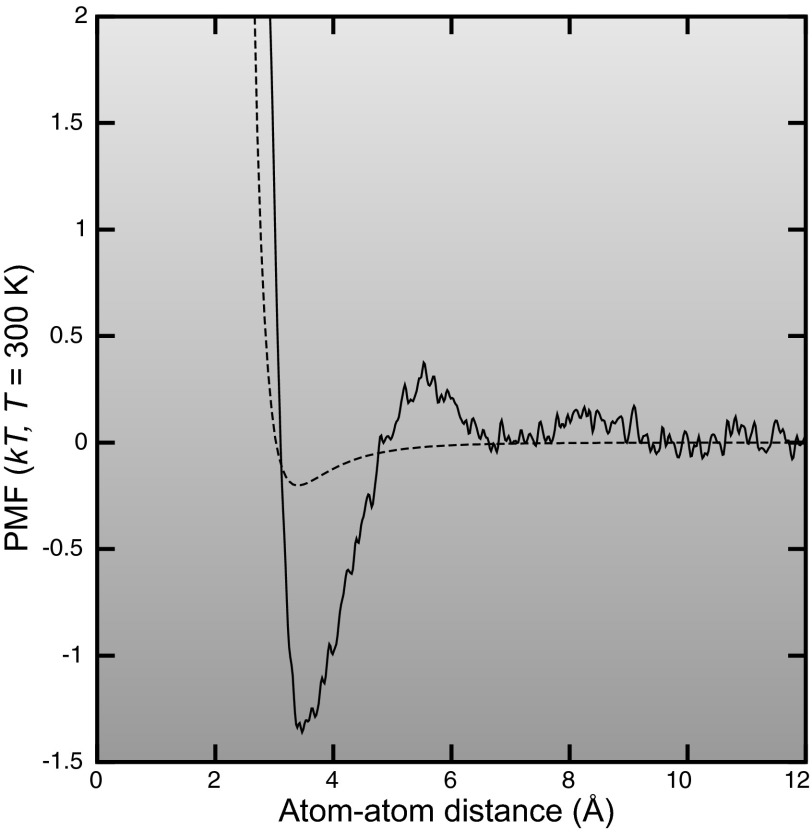
Water also plays an important role in effectively mediating nonpolar interactions between the atoms in ion channels, channel modulators, and ions. In the absence of water, such nonpolar interactions are described by van der Waals forces, and can be adequately modeled using Lennard-Jones potentials as described in the previous section. When water is present, it interacts in a complex manner with the solute molecules and strongly mediates the effect of the nonpolar forces. This is largely due to two factors. First, water exhibits strongly attractive van der Waals interactions with itself and other molecules. Therefore, when two solute atoms approach each other closely, some water is displaced, and there is an energetic cost to this displacement that needs to be taken into account when determining the nonpolar interactions between the two molecules. Second, water is not a perfect linear dielectric: its molecules have a finite size and exhibit a strong hydrogen bonding structure. When water is displaced by the presence of solute atoms, the hydrogen bonding network is modified. Water tends not to form hydrogen bonds with hydrophobic atoms. Adjacent to a hydrophobic surface, the water will compensate for lost water-solute hydrogen bonds by forming extra water-water hydrogen bonds, thereby creating a semi-rigid “cage” of surface tension around the atoms. The entropy of the water is lowered, which translates to a raising of the free energy. To minimize this free energy penalty, groups of hydrophobic atoms will therefore clump together so as to minimize their solvent exposed surface area. This is known as the hydrophobic effect and can be as important as hydrogen bonding in understanding the binding forces between channel modulators and ion channels. An example of water-mediated nonpolar interactions is shown in FIGURE 1.

Figure 1.

The potential of mean force between two neutral carbon atoms in the presence of water, calculated using 10 ns of metadynamics simulation. The dotted line shows the bare Lennard-Jones potential for comparison. The Lennard-Jones parameters are those of a carbonyl or guanadinium carbon atom, type C in the CHARMM27 force field. Since both atoms are neutral, the only direct forces between them are van der Waals forces. The presence of water is seen to greatly modify these van der Waals interactions, due to the hydrophobic effect and the varying effect of van der Waals forces between the atoms and water molecules as the atoms approach each other.

It is difficult to accurately take into account the effects described above when implementing implicit solvent force fields. The most common approach relies on linearly correlating the nonpolar hydration free energies of the solute with its solvent-exposed surface area. In some treatments, the hydrophobicity is taken into account by defining different scaling constants for different atom types; typically only a very small number of atom types are used. In more sophisticated treatments, a volume-dependent cavity term may also be included (81, 87, 86, 143). A surface area nonpolar hydration energy can be combined with the generalized Born approach to solvation, to give the often used generalized Born/surface area (GBSA) model of solvation.

3. Coarse graining and knowledge-based potentials

Coarse graining, the practice of treating groups of atoms as a single entity, represents a further level of abstraction in the hierarchy of force fields. The least radical form of coarse graining is to treat nonpolar hydrogens as being an implicit part of their parent atom, the so-called “united atom” approach seen in the CHARMM19 (202) and GROMOS force fields (209). More radical versions of coarse graining are also possible. The MARTINI force field (159), which was developed with the aim of modeling lipids and has been extended to proteins (169), is one example that has been used for ion-channel gating modifier studies (249). Each interaction center in the MARTINI force field represents approximately four actual atoms.

The parametrization in MARTINI was undertaken using similar principles to other all atom force fields such as GROMOS or CHARMM. In contrast, the so-called knowledge-based potentials (212, 227) are coarse-grained potentials that represent a very different, empirical approach to the general problem of free energies in protein binding. The basic idea is to use data obtained from sources such as the protein data bank to derive coarse-grained potentials, based for example on the distance between different types of residues. In the approach taken by Sippl (212), the distribution of various residue pairs as a function of distance is assumed to follow a Boltzmann distribution, and hence, knowledge-based potentials also tend to be called potentials of mean force, although there has been a good deal of theoretical debate about whether they do indeed represent rigorous potentials of mean force (18, 129, 172, 175, 231), and therefore whether they describe genuine free energies. Most relevant to the study of ion channel modulators are the various specializations of knowledge-based potentials to protein-ligand docking problems (e.g., see Refs. 90, 91, 168, 174, 214), some of which take a consensus scoring approach, with the knowledge-based potential score comprising only part of the docking score.

C. Computational Techniques

1. Molecular dynamics

Molecular dynamics has now become one of the most important computational tools for simulating biomolecular systems. The availability of several user-friendly packages such as AMBER (31), CHARMM (26), GROMACS (106), and NAMD (190) has made the method accessible to any researcher. With the increasing speed of modern computers, it will become increasingly possible to study in real time the interactions between polypeptide and ion channels at a microscopic level and relate the mechanisms of blockade to its underlying molecular structure.

In molecular dynamics simulations, we follow the trajectories of N particles interacting via a many-body potential using Newton's equation of motion. The equation is numerically solved using algorithms such as the Verlet (241) or velocity Verlet (224) algorithms. Such algorithms display the desirable properties of being time reversible and “symplectic.” In other words, the motion is derivable from some unknown Hamiltonian. This results in desirable stability properties, for example, energy is approximately conserved.

In addition to fully atomistic molecular dynamics, implicit solvent and coarse graining are sometimes used, as explained in the preceding section. To maintain computational speed, implicit solvent simulations usually use the generalized Born model of solvation rather than Poisson calculations. Various models may be used for the nonpolar hydration forces; surface area (SA)-based potentials are common.

Periodic boundary conditions are frequently employed in molecular dynamics; this can be convenient in biophysical systems which contain a lipid bilayer (since an endless bilayer can then be approximated by the periodic boundary) and water (since an infinite reservoir can be approximated). Because the Coulomb potential is a long-range pair potential, the time needed to compute the forces would, without special treatment, scale as the square of the number of particles. Fortunately, the electrostatics in periodic systems can be very efficiently treated using a technique known as particle mesh Ewald (60), which approximates the periodic potential using fast Fourier transforms. Furthermore, modifications to the propagation algorithm can be used to give constant pressure and temperature dynamics (19, 235).

A typical molecular dynamics simulation of a channel-blocker system would first contain the ion channel model. Frequently, this will be truncated to include only the pore-forming domain and might contain close to 10,000 atoms. This would be embedded in a lipid bilayer containing a couple of hundred lipid molecules, or around 20,000 atoms. There might be a further 20,000 water molecules surrounding the system. The complete system might contain close to 100,000 atoms and have a size of around (100 Å),² of which only ∼10% would relate directly to the channel/blocker system, the rest being made up of lipids and water.

Typical molecular dynamics simulations are too computationally intensive to directly observe events such as ion channel conduction and block and the binding dynamics of modulators. For the system described above, and using a modern supercomputer, it might be possible to perform several dozen nanoseconds of continuous simulation in a reasonable timeframe, whereas the dynamics of a channel modulator interacting with a channel would evolve on timescales of microseconds or perhaps much longer. Costly purpose-built hardware can increase the simulation timescale to microseconds (116). Thus simulations are usually employed to explore the stability and energetics of bound complexes, sometimes with the help of the free energy techniques described in section IIID, and to observe details of docked complexes such as atom-atom and contacts, hydrogen bonding, and so on. Another use for molecular mechanics is to refine docked poses that may have been produced by docking programs or manually.

2. Brownian dynamics

Brownian dynamics simulations of ion channels use two key assumptions to speed up the simulation: the ion channel is assumed to be a rigid or mostly rigid structure, and the solvent is assumed to be implicit. The cell membrane is usually represented as an idealized dielectric slab. Implicit solvent electrostatics is usually employed, and frictional and random forces are introduced to model the Brownian motion induced by the solvent and other atoms in the system (50). In most ion permeation studies, therefore, the only moveable objects are the ions, which are usually simulated using the Langevin equation or first-order Brownian motion. In studies involving blocker molecules, additional mobile blockers also need to be simulated.

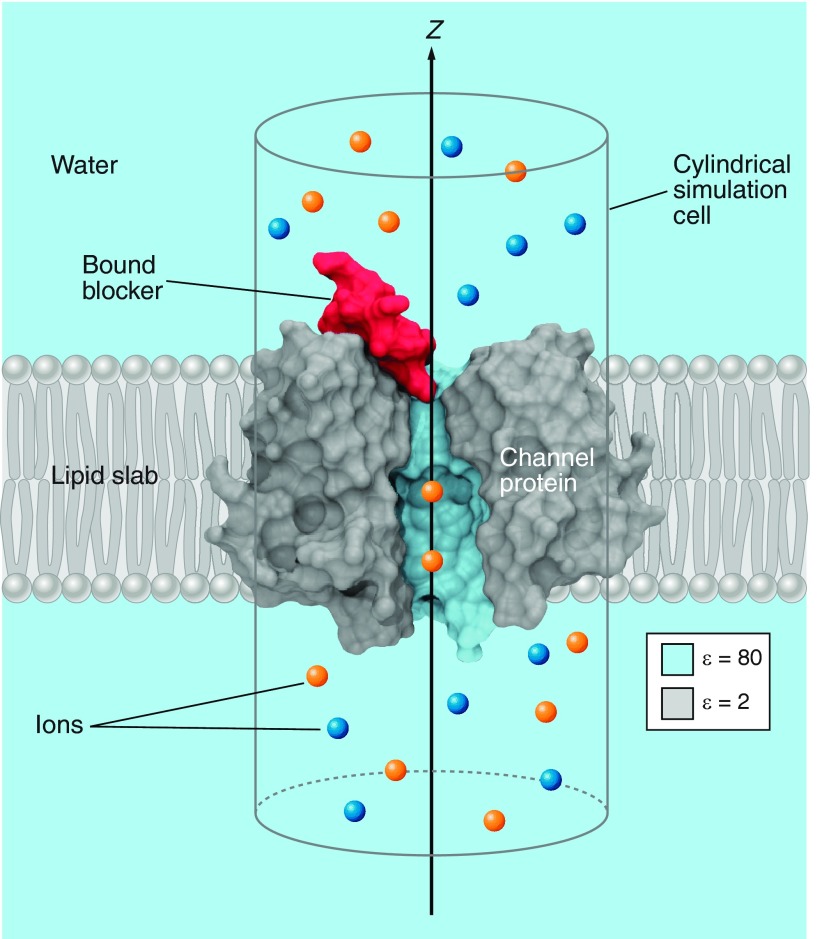
The electrostatics of the channel may be handled efficiently by presolving Poisson's equation for various configurations of mobile charges (50). Other forces, for example, steric repulsion, are handled in a variety of ways depending on the particular model. Alternative ways of deriving the forces exist, often based on prior molecular dynamics PMF calculations, or other molecular dynamics sampling (21, 27, 74, 92). Compared with molecular dynamics and docking, the use of Brownian dynamics for ion channel blocker studies is in its infancy. A typical Brownian dynamics simulation cell (such as that used by Gordon et al., Ref. 97) is shown in FIGURE 2.

Figure 2.

A typical Brownian dynamics simulation cell. The channel, shown in gray, is embedded in an idealized lipid slab. Water surrounds the channel and lipid, and also permeates the pore of the channel. A low dielectric constant (2 here) is assigned to the channel and lipid region and a high dielectric constant to the water-filled region. A cylindrical simulation cell is defined as shown. Simulation bodies are the rigid-body blocker, shown in red, and the ions, shown in blue and orange.

The simplest application of Brownian dynamics to the study of ion-channel block relates to ionic block, since only monatomic ions need be considered (55, 56, 57, 242). In studies involving molecular ion channel blockers, which are more relevant to the development of treatments for diseases, the rotational motion of the blocker molecules needs to be taken into account. It is possible to treat the blocker either as a single rigid body, a set of coupled rigid bodies, or as a fully flexible object using a molecular mechanics force field. In the first two cases, a rigid-body motion algorithm will need to be employed (16, 77, 95, 182). There exist very few Brownian dynamics studies of channel-blocker interactions (59, 58, 84, 97). To date, these have employed fully rigid models for the channel and blocker and therefore suffer from many of the same problems as rigid-body docking. Recently, Brownian dynamics has been proposed as a docking protocol (163).

While it is relatively easy to implement rigid body rotational motion algorithms (95), the treatment of force fields is much more challenging. The same problems that exist in all implicit solvent systems, the accurate and fast representation of the electrostatics and the treatment of nonpolar hydration forces, also apply to rigid body Brownian dynamics. Unlike implicit solvent molecular dynamics, the assumption of relatively rigid channels and blocker molecules introduces the possibility to use lookup tables for the electric field instead of resorting to approximations such as the generalized Born approximation, although the treatment of electrostatic self energies is difficult (98). As has been remarked previously, the strong electric fields that run through the pores of ion channels may perhaps render the usual (e.g., GBSA) approaches to solvation inaccurate. In the future, it would be advantageous to extend Brownian dynamics studies of blocker channel interactions by first taking into account some degree of flexibility in the blocker and perhaps the channel. A careful treatment of the electrostatics, nonpolar and solvation forces will also be needed to correctly model the energetics.

The use of rigid body blockers with fixed channels in Brownian dynamics presents a serious obstacle to achieving the correct docking poses of the blocker. This is particularly so in the case of large polypeptide blockers, which usually have a very rigid backbone but bind with the aid of flexible basic side chains that form salt bridges to acidic residues on the channel. The flexibility enables several sidechains to locate closely at favorable sites on the channel, while also avoiding unfavorable electrostatic interactions or steric clashes. It is also likely that channel flexibility will also play some role in efficient binding. For example, the narrow selectivity filters of voltage-gated potassium channels must make subtle adjustments to accommodate the insertion of blocker lysine residues. Another example is the possibility that the outer vestibules of channels may also undergo changes to accommodate the shape of the blocker molecule, increasing hydrophobic binding and eliminating steric clashes. Finally, a more problematic example concerns the presence of highly mobile “turret” loops in the outer vestibule of many channels. These turrets may contain interaction sites for the blocker; their conformation can affect binding. Note, however, that this latter example creates problems not only for Brownian dynamics and docking, but also for molecular dynamics, since the conformational movement of the turret regions can be very slow.

In principle, a number of steps may be taken to alleviate the problems mentioned above. The most radical solution would be to introduce a large degree of flexibility with the aid of implicit solvent molecular mechanics. This approach would blur the division between Brownian dynamics and molecular dynamics. The use of lookup tables would be made problematic in such an approach, and might need to be replaced by the use of generalized Born electrostatics, for example. Simulation speed would become a serious consideration in this approach.

The ability of selectivity filters to make subtle adjustments to accommodate the insertion of side chains might be improved by allowing single atoms, such as the carbonyl oxygens that line the filter in Kv channels, to move in a harmonic potential. This was in fact tried by Chung and Corry (51) for modeling ion permeation in the KcsA potassium channel.

Finally, the blockers and channels might be modeled using multiple coupled rigid bodies. For example, lysine and arginine side chains in blocker molecules could be coupled to the core of the blocker via various types of “hinge” constraint. This latter approach is reminiscent of the treatment of flexibility in many docking programs. The authors of this review have in fact implemented this approach and are currently quantifying its effect.

3. Docking

Docking is a computational procedure that aims to produce docked “poses” representing complexes between the receptor and the docked ligand or protein. It is a rapidly growing and complex field. Compared with the other theoretical methods discussed in this review, there is a high degree of arbitrariness and pragmatism in the various combinations of theoretical and heuristic techniques that are employed to rapidly dock candidates into receptors. In terms of ion-channel research, the primary aim is to find and rank docked complexes of a channel modulator molecule with the channel protein, with an emphasis on speed. To achieve this aim, docking programs need both a search algorithm that explores the available configuration space of the channel-ligand system to identify favorable complex geometries, and a scoring function that applies various considerations to rank the complexes in line with their free energies of binding.

Original docking systems such as DOCK (133) employed only rigid docking, where both the ligand and receptor are rigid bodies. In rigid docking, the search can operate in an approximately exhaustive manner, by attempting to explore all possible docked positions and orientations of the ligand. To speed up the search, it is common to use precalculated scoring grids. For each type of atom in the ligand, chemical and physical data (e.g., electrostatic energy, hydrogen bonding, etc.) and geometric data (steric clashes, etc.) relating to that type of atom is calculated on a grid of atom positions relative to the receptor. These grids are then consulted during the subsequent search, to rank the candidate poses. The search itself may be performed by a number of methods, including fast Fourier transform techniques, as employed in ZDOCK (36), GRAMM (238), and DOT (158).

As was the case for rigid body Brownian dynamics, rigid docking presents serious difficulties for the study of ion-channel modulators, as the modulator, especially the large peptide toxins, or the channel, as in the case of potassium channels with their unordered loop turret regions, can exhibit substantial flexibility. Careful alignment of the key functional groups is frequently needed to achieve strong binding. A flexible docking approach is usually required. Most modern docking programs include some means of treating flexible docking, and there are several ways in which this might be done.

One simple approach, which is really just an extension of rigid-body docking, is “soft docking,” where the force field is modified to reduce the effects of steric clashes and slight misalignments. This approach is very common in rigid docking, and in the initial stages of many docking programs in general. For example, the GRAMM docking software (238) uses a smoothed energy function to consider docking at a low spatial resolution; it has been used in protein-protein docking studies involving ion channels (186, 219).

Another approach, ensemble docking (110), considers an ensemble of ligand or receptor conformations. The ensemble could be obtained from unbound simulations of the ligand and/or receptor, or from multiple conformations found in databases such as the protein data bank. The assumption here, which has been shown to be reasonable, is that unbound simulations of receptors and ligands will tend to approximately sample bound conformations (24, 144, 198), and therefore using such ensembles can effectively take account of induced conformational fit of the ligand and/or receptor. Ensemble docking can be performed in an ad hoc manner, simply carrying out multiple rigid docking runs using different conformations of the molecules (198, 199), or using more efficient structured algorithms (53, 82).

A more direct but computationally intensive approach to flexibility directly explores the conformational space of the ligand and possibly the receptor site. This is often done on a restricted basis by defining bonds around which rotations can be made, such as rotations of side chains around their C_α bond. To accommodate the increased dimensionality of the problem, it will in most cases no longer be possible to perform a systematic search over the configurational space. Instead, techniques such as genetic algorithms [employed in AUTODOCK (170) and GOLD (239)], simulated annealing [employed in HADDOCK (44, 70)], or Monte-Carlo sampling [employed in GLIDE (204) and MCDOCK (150)] are required.

Lastly, there is the “anchor and grow” approach to ligand flexibility. Initially, a rigid “core” of the ligand is docked into the receptor site. The flexible parts are then incrementally added to the core in a manner that minimizes the free energy function and avoids steric clashes. Anchor and grow is implemented in the latest versions of the DOCK software (136).

Protein-protein docking, which is relevant to polypeptide channel modulator toxins, is considered to be far more difficult than protein-ligand docking (8, 24, 99, 198), due to the need for a large degree of flexibility, including backbone flexibility in many cases. Docking programs specialized to protein-protein docking, or used in protein-protein docking studies, include BiGGER (184), DOT (158), HADDOCK (70, 62), GRAMM (238), and ZDOCK (36).

The docking protocols used in most of the docking programs mentioned above can be complicated and may involve multiple stages of increasing refinement. For example, it is common to perform an initial crude docking stage, after which candidates are ranked using more exact force fields. The most promising candidates may then be refined further, and so on.

Along with search and refinement algorithms, the scoring functions used by docking programs form a key determinant of their success or failure. There are myriad approaches to scoring, and it is common for docking programs to give the user a choice of scoring function, or to employ several different scoring functions at different stages of search and refinement. Scoring functions may be classified according to whether they are force-field based, using molecular mechanics type physics based force fields, empirical, using scoring functions for complex forces such as hydrogen bonding that are derived from regression analysis against known affinities, or knowledge based, where the scoring function is based on large-scale coarse-grained structural information gleaned from protein databases.

Entropy presents a particular complication to scoring. Using rigid or partially rigid molecules means that entropic contributions to the free energy that result from the internal degrees of freedom of the molecule are not present. Furthermore, most docking algorithms will also tend to ignore the entropic penalty that arises when a ligand that is free to move and rotate in solution is confined by a binding site. Empirical or semiempirical scoring functions may in part implicitly compensate for this fact through the optimization of their parameters to a training set. Explicit entropic contributions, such as penalties arising when rotatable bonds are frozen by the formation of a contact, are also frequently employed (75).

As an example of a typical approach to rapid scoring used for rigid docking, the scoring algorithm used by the ZDOCK algorithm can apply three scoring components: shape complementarity, desolvation, and electrostatics. Shape complementarity penalizes steric clashes and rewards surface-surface contacts. It is implemented by defining functions of the atomic coordinates on grids. Two variations for the grid functions have been devised (36, 37). The scoring function is then defined as a sum involving terms bilinear in the receptor and ligand grid functions. Electrostatics is carried out using scaled Coulomb potentials, and therefore, the complexities of the dielectric structure of the system are only taken into account in a very approximate manner. Desolvation is treated in a similar simplified manner, using empirically derived estimates of the free energy of forming pairwise atom-atom contacts. More recent versions of ZDOCK may employ a slower, but more accurate, statistical potential (167).

An example of an empirically derived scoring function is ChemScore (75), used by GOLD (239). This scoring function defines only six atom types and considers simple pairwise contact and longer range free energy terms for hydrogen bonding, metal contacts with donors or acceptors, lipophilic interactions, and entropic penalties for frozen rotatable bonds. The parameters are set based on regression analysis using a training set. The rationale behind this kind of force field is that precise functional forms are not important, as the regression will tend to compensate for the particular features of the chosen functions, and will tend to average out the effects of insufficiently precise data, for example, in the use of very general atom types. Autodock Vina (234) is another example of an empirical potential, containing terms for steric repulsion, hydrophobic bonding terms, and hydrogen bonding terms. The force field parameters are optimized to the training set using a stochastic global optimization algorithm.

Autodock4 (113) uses a semiempirical approach to scoring. Pairwise atom-atom potentials are defined, using van der Waals potentials based on the Amber force field, a hydrogen bonding term, screened Coulomb electrostatics with a distance-dependent dielectric constant, and a desolvation term. Each of these terms is further multiplied by an empirical weighting factor optimized based on a training set, which allows the scoring function to implicitly compensate for factors, such as entropic penalties, not taken explicitly into account.

DOCK6 (136) allows a variety of scoring functions to be employed, including a full force-field based scoring function, Amber Score that more or less implements the full AMBER molecular mechanics force field (30, 244) with generalized Born solvent-accessible electrostatics and desolvation. This allows flexibility of the ligand and receptor to be dealt with in a natural manner, and structure refinement to be carried out.

Knowledge-based potentials have also been fruitfully applied to the problem of scoring. As discussed earlier in this review, knowledge-based potentials are based on the assumption that in a library of proteins or ligands, structural determinants such as the observed distance between atoms of various types are distributed according to Boltzmann factors, allowing potentials of mean force to be defined that accurately reflect the free energy of the system. For example, the DrugScore scoring function (90) uses knowledge-based distance-dependent pair-potentials along with single-atom potentials describing the preference of atoms to be solvated or buried.

A rather different approach, used in the HADDOCK program (43, 70, 62), uses experimental data about the distance between functional groups (which might be taken from analysis of NMR studies, or from mutant cycle analysis) to define distance restraints, which are then applied in the force field.

There are dozens or more studies of ion-channel modulators that employ docking software; the following references provide a sample of these: 1, 4, 6, 7, 20, 28, 43, 49, 66, 80, 85, 89, 102, 131, 149, 155, 161, 181, 186, 192, 193, 196, 197, 199, 201, 219, 233, 257, 260, 266.

4. Quantitative structure-activity relationships

Although quantitative structure-activity relationships (QSAR) are somewhat out of the scope of this review, we mention it here due to its potential usefulness in drug discovery, especially at the early lead screening stages where thousands of compounds may need to be considered. QSAR studies represent a very high level of modeling that is often applied in the drug design world. A number of attributes of different candidate drugs are defined. Attributes can be quantities such as hydrophobicity, polarizability or refractivity, or spatial structural information. The attributes are tabulated along with their activity (for example, in ion channel studies the activity could refer to the inhibitory constant, IC₅₀). Then, essentially, a regression analysis is performed. The results can be used to predict the activities of as yet untested compounds. Numerous QSAR studies have been performed on ion channels (see, for example, Refs. 11, 176, 206, 226).

III. ENERGETICS AND BINDING THEORY OF MOLECULAR COMPLEXES

In the preceding sections, we introduced several types of force fields and computational techniques that are used in computational studies of ion channel modulators. In the following section, we will take a more detailed look at some of the theory and applications used in the computational studies that employ these techniques. In particular, we will discuss the theory of binding affinity, a key metric by which blockers and other modulators may be assessed, and computational methods by which it may be calculated.

Binding affinity measures the strength with which a channel modulator is bound to an ion channel. Its inverse, the dissociation constant, predicts the propensity of complexes to break up. Statistical mechanics shows us that this key experimentally measurable quantity is directly related to the free energy of binding of the complex, the work needed to unbind the complex in a reversible manner. Because it is easier to compute free energies than to directly perform measurements of binding affinity, the free energy of a complex is perhaps the single most important theoretical quantity to consider when computationally assessing the effectiveness of a candidate channel modulator. Unfortunately, calculating the free energy of a biomolecular complex is not an easy matter. It depends in principle not just on a single complexed state, but also on all possible configurations of water and other extraneous parts of the system, as well as all possible bound, unbound, and intermediate states of the channel modulator.

We will begin our treatment of energetics and binding with a discussion of free energy. We will then define the dissociation constant and show how the free energy and dissociation constant are related. Finally, we will look at the computational methods used for calculating or estimating free energies of binding and, hence, the dissociation constant. The following sections are quite theoretical, and the reader may choose to skip ahead if desired.

A. Free Energy and Potentials of Mean Force

Suppose that we have a canonical (N, V, T) ensemble, with fixed particle number N, volume V, and temperature T. The most important quantity, from the point of view of ligand binding experiments, is the Helmholtz free energy³ of the system, F = E − TS, where E is the average total energy, T is the temperature, and S is the entropy. Free energy has a direct relationship with the probability of the system being in a given macrostate, whereas such a relation does not hold for, say, the average potential energy of a macrostate.

Suppose we have a system, whose state space is Γ₀, the set of all possible microscopic configurations of particles. We are interested in the probability of finding the system in a macrostate Γ_b, which we will take to consist of the blocker bound to the channel. We first calculate the free energy Γ_b relative to Γ₀

$$\Delta F=E_b-E_0-T\left(S_b-S_0\right)$$ (10)

Here, E_b and E₀ are the average total energy for the bound macrostate and the whole state space, respectively, and S_b and S₀ are the corresponding entropies. We can write down the probability of the blocker being bound as

$$P\left(b\right)=\exp \left(-\Delta F/kT\right)$$ (11)

Note that this probability contains an energetic contribution, from E, as well as an entropic contribution, from S. The entropy, S, of a macrostate is, broadly speaking, a measure of the number of possible microstates that belong to the macrostate. The higher the entropy, the higher the probability of the system being in that macrostate.

The discussion given above refers only to macroscopic quantities such as entropy and total energy. Statistical mechanics shows us how these concepts can be related to microscopic states of the system. According to statistical mechanics, the probability of the system being in the bound macrostate Γ_b is

$$P\left(b\right)=\frac{Z_b}{Z_0}$$ (12)

where the (configurational) partition function Z_s for a state s (with s = b or 0) is

$$Z_s={\displaystyle {\int }_{{\Gamma }_s}\exp \left(-U/kT\right)}$$ (13)

where U is the potential energy of the system, with the integral being taken over all microstates in either the bound or total macrostates. Since we are just concerned with probabilities, which always hinge on ratios of partition functions, we have omitted some constant factors in front of the partition functions. The free energy of binding can then be defined as

$$F_b=-kT\hspace{0.17em}\text{ln}\left(\frac{Z_b}{Z_0}\right)$$ (14)

so that the binding probability is always exp(−F_b/kT). This makes the link between the definition of F in terms of energy and entropy, Equations 10 and 11, and the statistical mechanical definition in terms of integrals over microstates.

The concept of free energy allows us to separate the degrees of freedom of the system that are directly relevant to the binding process, such as the positions of the blocker and channel, from those that are not directly relevant, such as the configuration of all water molecules. This is possible because the relevant degrees of freedom can be used to define the macrostates while irrelevant degrees of freedom are ignored, as for example when center of mass distances are used to define bound and unbound states independently of the positions of water molecules. Suppose we measure the center of mass of the blocker relative to the channel. This quantity is a continuous (vector) parameter which selects subsets of the configuration space; in this case, these subsets are the macrostates where the blocker lies at a certain position r_COM relative to the channel. The free energy w(r_COM) of each of these macrostates, as a function of the reaction coordinate, is termed the “potential of mean force” (PMF). The symbol w, rather than F, is typically used to denote that the free energy is expressed as the function of a continuous set of reaction coordinates. The PMF is important because its gradient gives the average force along the reaction coordinate, just like a real potential. In the example here, the average force on the blocker is −∇w.

The PMF in the example above is defined on a three-dimensional domain, but it is also common to define one-dimensional PMFs. For an ion channel with approximate cylindrical symmetry running along the z-axis, it is common practice to take the projection of r_COM on the z axis, or alternatively on an instantaneous axis of the channel, as the reaction coordinate z_COM for a one-dimensional PMF. The PMF for the blocker unbinding from the channel is then the free energy, as a function of z_COM. When the blocker is a long way from the channel, it is free to wander to infinity in the x-y plane, and hence its free energy relative to the bound state will be negative infinity. Recall that we are working in a framework where there is a single channel and blocker, rather than concentrations of each. If the blocker is free to wander infinitely far from the channel, this will physically correspond to zero concentration of blockers, and binding will never be observed. To have a well-defined one-dimensional PMF, therefore, some kind of restraining potential is necessary. It is common to confine the blocker using a cylindrical flat bottomed harmonic potential

$$U\left(r\right)=\{\begin{array}{lll}\frac{1}{2}k{\left(r-R\right)}^2\hfill & :\hfill & r>R\hfill \\ 0\hfill & :\hfill & r\le R\hfill \end{array}$$ (15)

such that the blocker is free to move around within the interior of a cylinder of radius R but is prevented from moving out of this cylinder by a strong harmonic force. Adding the cylindrical restraining potential means that the one-dimensional PMF will be calibrated to the blocker concentration set by the cylinder.

The process of actually obtaining potentials of mean force and free energies will be explored in a later section, but it is clear from the discussion above, and in particular from Equations 13 and 14, that free energies are a function not of single microstates, but rather of large ensembles of microstates, and for this reason their calculation can be very difficult.

B. Dissociation Constants

In the discussion above, we have explained how the concept of free energy is relevant to binding probability, and how it relates to channel-blocker systems. Binding probability is usually observed experimentally by performing assays which measure the percentage of bound blockers in a solution containing blockers and channels, or indirectly by measuring the actual block of current caused by the blockers. In such experiments, values such as the binding affinity or its inverse, the dissociation constant, are most relevant.

Assume we have a solution containing concentrations of unbound channels [C], unbound blockers [B], and channel-blocker complexes [CB], at equilibrium, we find that the quantity

$$K_d=\frac{\left[C\right]\left[B\right]}{\left[CB\right]}$$ (16)

is a constant, independent of the concentrations. We call this quantity the dissociation constant, as it measures the propensity of [CB] to separate into components [C] and [B]. If half the total channels are bound, then [C] = [CB] and hence K_d can be interpreted as the concentration of free blockers [B] at which half the channels are bound. The fact that K_d is in fact constant is not immediately apparent from the equation above, but can be justified on microscopic grounds, at least in the limit of low binding probability.

C. Statistical Mechanical Treatment of Binding

Binding assay experiments measure dissociation constants. To relate the results of such experiments to theoretical calculations, we need a way to relate the dissociation constant to the microscopic details of the channel-blocker interaction. Not surprisingly, the key quantity turns out to be the free energy of channel-blocker binding. The reason this is the case is that both the free energy of binding and the dissociation constant are directly related to the binding probability.

Suppose we have a large volume V containing c channels and b blockers. Further suppose that the channels and blockers do not interact, except when a blocker enters a small binding pocket located on the channel. Because the channels are assumed not to interact with each other, the energy of the system does not depend on their positions, only on the positions of the blockers relative to the channels. Thus, although the problem can be formulated more rigorously to arrive at the same result, we can assume that all channels occupy fixed positions. Taking the reference energy for an unbound blocker to be zero, each blocker then contributes an amount equal to the volume V to the partition function, Equation 13, as it ranges over the free space between the channels. Furthermore, in forming the partition function, the blockers also range over the binding pockets of the channels, contributing an amount

$$I={\displaystyle {\int }_{\text{binding}\hspace{0.17em}\text{site}}\exp \left(\frac{-w\left(x,y,z\right)}{kT}\right)\text{d}x\hspace{0.17em}\text{d}y\hspace{0.17em}\text{d}z}$$ (17)

to the partition function per interaction, where w is the blocker-channel PMF. We can now write the partition function as a sum over the number of complexes i. The maximum number of complexes that can be formed is the minimum of b and c. We need to multiply each term in the sum by a multiplicity factor that counts the number of ways of forming i complexes using c channels and b blockers: this is

$$\text{multiplicity}=\frac{c!b!}{i!\left(c-i\right)!\left(b-i\right)!}$$ (18)

Putting all of this together, we can finally write down the partition function

$$\begin{array}{c}{Z}_{c,b}={\displaystyle \sum _{i=0}^{\min \left(c,b\right)}{Z}_{i;c,b}}\\ ={\displaystyle \sum _{i=0}^{\min \left(c,b\right)}\frac{c!b!}{i!\left(c-!\right)\left(b-i\right)!}{V}^{b-i}{I}^i}\end{array}$$ (19)

We can then find the average number of complexes as

$$\begin{array}{c}<i>=\frac{1}{Z_{c,b}}{\displaystyle \sum i{Z}_{i;c,b}}\\ =\frac{cbI}{V}\frac{Z_{c-1,b-1}}{Z_{c,b}}\end{array}$$ (20)

This equation shows how the average number of complexes depends on the properties of the sum Z. Here, we analyze only very dilute solutions, where the binding probability will be small and thus we can throw away all terms but the leading terms Z_0;c,q in the sums above. Doing so gives

$$<i>=\frac{cbI}{V}$$ (21)

The binding probability is simply the average number of complexes divided by the number of channels

$$\begin{array}{c}{P}_{\text{bind}}=\frac{<i>}{c}\\ =\frac{cbI/V}{c}\\ =\left(\left[B\right]+\left[CB\right]\right)I\end{array}$$ (22)

where we measure concentration in units of number density. But we can also express the binding probability directly using the bound and unbound channel concentrations

$$P_{\text{bind}}=\frac{\left[CB\right]}{\left[C\right]+\left[CB\right]}$$ (23)

and thus, from Equations 22 and 23,

$$\begin{array}{c}I=\frac{\left[CB\right]}{\left(\left[C\right]+\left[CB\right]\right)\left(\left[B\right]+\left[CB\right]\right)}\\ \approx \frac{\left[CB\right]}{\left[C\right]\left[B\right]}\left(\text{dilute},\hspace{0.17em}\text{low}\hspace{0.17em}\text{binding}\hspace{0.17em}\text{prob}.\right)\\ =K_d^{-1}\end{array}$$ (24)

The importance of this equation is that the dissociation constant K_d is directly related to the standard free energy of binding, which is defined as −kT ln(C₀I), where C₀ is the standard concentration of 1 M. The binding probability itself is proportional to I. The fact that I does not depend on the channel and blocker concentrations shows that K_d really is constant, at least in the limit of low binding probability.

It remains to relate this equation to the typical geometry used in calculations involving ion channels (see FIG. 3). I represents the integral of the probability density over the binding pocket (Eq. 17), which is somewhat arbitrary. However, in typical cases involving binding in ion channels, the binding pocket is a deep potential well, and the presence of the exponential in the integral ensures that by far the dominant contribution comes from bound states even if the integral is taken over a region slightly larger than the actual binding pocket. We only need to make sure that the region is large enough to include the entire binding pocket. Due to the approximate cylindrical symmetry of ion channels and for convenience of calculation, normally I is calculated using a cylinder of radius R whose axis runs along the axis of the channel, with one end of the cylinder z₀ extending past the location of the binding pocket on the channel side, and the other end z₁ extending far enough into the bulk region that the PMF is close to its value in the bulk. The radius of the cylinder is chosen based on two competing considerations. We wish to avoid excluding any interactions contributing to the binding process (meaning R should be large), and we wish to avoid making our sample space too large in order that the simulation may converge (meaning R should be small).

Figure 3.

Typical geometry for 1-dimensional PMFs. In this figure, the channel is depicted in gray and the blocker in red. The z-axis runs along the axis of the pore. The blocker is confined within a cylinder of radius R_cy1. The z coordinate of the blocker center of mass, relative to the channel, defines the reaction coordinate z_com.

As defined in Equation 17, I involves a three-dimensional integral over the binding pocket. This can be achieved using a one-dimensional potential of mean force. Suppose the PMF w₃(x, y, z) is defined on the cylindrical region discussed above, where the z coordinate runs along the axis of the channel and the cylinder. Then the one-dimensional PMF w₁(z) is defined by

$$\pi R^2\exp \left[-w_1\left(z\right)/kT\right]={\displaystyle {\int }_{\text{circle}\hspace{0.17em}R}\exp \left[-w_3\left(x,y,z\right)/kT\right]\text{d}x\hspace{0.17em}\text{d}y}$$ (25)

Integrating πR² exp[−w₁(z)/kT] over z is equivalent to integrating exp[−w₃(x, y, z)/kT] over the whole cylinder. The factor πR², which acts as an energy offset for w₁, is inserted for convenience so that, in the bulk (z = z₁), w₁ can be defined to be at zero energy; its purpose is to set the conversion between number density and linear number density. We then have, from Equation 24,

$$K_d^{-1}=\pi R^2{\displaystyle {\int }_{z0}^{z1}\exp \left[-w_1\left(z\right)/kT\right]\text{d}z}$$ (26)

Finally, note that for ease of calculation we have been expressing concentrations in number density: to convert K_d from SI number density to the more normally used moles per liter, we need to insert a factor of 1,000 N_A into the equation

$$K_d^{-1}=1000\pi R^2{N}_A{\displaystyle {\int }_{z0}^{z1}\exp \left[-w_1\left(z\right)/kT\right]\text{d}z}$$ (27)

A similar, but slightly less general, analysis can be found in Woo and Roux (256).

D. Free Energy Methods

Since the free energy of binding is the ultimate determinant of binding affinity, it is perhaps the most important goal of theoretical and computational studies to predict this quantity. Unfortunately, its prediction is extremely difficult, even for small blocker molecules. For large molecules such as polypeptide toxins, binding free energies have been computed (39, 41, 42, 44, 45, 47, 48, 94), but such calculations use simulation times that are smaller than ideal, and hence their accuracy is still open to question.

In all free energy calculations, we wish to calculate the change in free energy as the state of the system is changed from one macrostate to another. We take the first macrostate, state A, to be the state where the blocker is bound, and the second, state B, to be the unbound state. The change in free energy can be expressed as

$$\begin{array}{c}\Delta F=-kT\hspace{0.17em}\text{ln}\hspace{0.17em}\left(Z_A/Z\right)+kT\hspace{0.17em}\text{ln}\left(Z_B/Z\right)\\ =-kT\hspace{0.17em}\text{ln}\hspace{0.17em}\left(Z_A/Z_B\right)\end{array}$$ (28)

where Z_A and Z_B are the partition functions for states A and B, respectively, and Z is the total partition function. Because the partition functions involve integrals over microstates, we can see that the free energy of binding involves integrals over all bound and unbound states of the system, and is therefore likely to be very computationally costly to compute. Furthermore, it is not feasible to directly compute the partition functions Z_A and Z_B, meaning we cannot just simulate the bound and unbound states and directly derive the free energy difference. Instead, other means must be used to compute the free energy. The most rigorous methods attempt to calculate the free energy according to Equation 28 by calculating free energy differences along a continuous path connecting the bound and unbound states. Other approximate methods exist, where only the endpoints of the path (the bound and unbound states) are sampled, and other approximations of the physics, such as using implicit solvent, or regression methods, are employed. The most approximate methods rely on coarse graining, where only a limited subset of the binding data is used to estimate the free energy, with parameters developed based on extensive data from the protein data bank. Starting at the most rigorous end of this hierarchy, we shall discuss the main methods for calculation of free energy of binding in turn.

1. Free energy perturbation and thermodynamic integration

We can write the free energy ΔF as

$$\begin{array}{c}\Delta F_{A,B}=-kT\hspace{0.17em}\text{ln}\left(\frac{Z_A}{Z_B}\right)\\ =-kT\text{ln}\left(\frac{Z_A}{Z_1}\frac{Z_1}{Z_2}\cdots \frac{Z_{n-1}}{Z_n}\frac{Z_n}{Z_B}\right)\\ =-kT\text{ln}\left(\frac{Z_A}{Z_1}\right)-kT\text{ln}\left(\frac{Z_1}{Z_2}\right)\cdots -kT\text{ln}\left(\frac{Z_{n-1}}{Z_n}\right)-kT\text{ln}\left(\frac{{\text{Z}}_{\text{n}}}{{\text{Z}}_{\text{B}}}\right)\\ =\Delta F_{A,1}+\Delta F_{1,2}+\cdots +\Delta F_{n-1,n}+\Delta F_{n,B}\end{array}$$ (29)

If we now assume that state A is close to state 1, state 1 is close to state 2, and so on, this shows that the free energy can be written as a sum of small free energy differences between a sequence of states connecting A and B in a nearly continuous manner. It is possible to define these various states as the equilibrium states of different potential energy functions; so, for example, the potential energy function for the unbound state B would contain terms making it energetically unlikely for the system to be in the bound state A.

The first main idea behind the free energy perturbation technique is that the intermediate states 1, 2, … in the equation above need not represent physical states of the system. Thus, to make the transition from the bound blocker to the unbound blocker, we can employ two blocker molecules, one bound and one in bulk. Initially, the potential energy is defined so that the blocker in the bulk does not interact with the other molecules in the simulation at all: it is “turned off” and has zero potential energy. With each successive term in the sum above, the interactions between the bound blocker and the rest of the system can be gradually turned off while the interactions between the unbound blocker and the rest of the system are gradually turned on. In other words, the bound blocker is gradually made to “disappear” while the unbound blocker is made to “appear.” The free energy differences at each step are added, and the result is, in theory, the free energy of binding.

The second idea behind these methods is that, if successive terms in the sum above are sufficiently close, then the free energy difference can be calculated as, e.g.,

$$\Delta F_{1,2}=-kT\hspace{0.17em}\text{ln}{\langle \exp \left[-\beta \left(U_2-U_1\right)\right]\rangle }_1$$ (30)

where the average is taken by evaluating the potential energy difference U₂ - U₁ over an ensemble generated using U₁ alone. Note that the potential energy, rather than the total energy, can appear in the expression above for ΔF because the kinetic energy dependence will cancel out in the canonical ensemble when states 1 and 2 depend on position alone.

The technique just described is known as the free energy perturbation technique: the terms in Equation 29 represent discrete jumps of the potential energy function. If we instead smoothly vary the potential energy function according to a parameter λ, and integrate du/dλ instead of summing ΔU at each step, then we arrive at the related technique of thermodynamic integration.

In practice, these techniques have practical difficulties when calculating the absolute binding affinities of blockers. For example, the Lennard-Jones and electrostatic potentials need to be softened to overcome their infinitely large cores, and entropy effects that arise just before the states vanish, or have just started to appear, can also create problems. More seriously, the “disappearing” and “appearing” blocker paradigm means that the free energy is expressed as the difference between two extremely large energies. The error in such a difference might be on the order of many kT. On a somewhat stronger footing is the use of either technique to calculate the relative free energy difference between two similar blockers: the bulk of the blocker remains the same, while one functional group is mutated into another (88).

2. Potential of mean force via umbrella sampling

The potential of mean force represents the free energy of a system relative to a reaction coordinate, which, for example, can be the center of mass of a blocker relative to a channel. The free energy of binding can be calculated from the PMF by straightforward integration.

The most direct means to find free energy differences is to just simulate the system and calculate the ratios of observed probabilities. For example, the free energy of binding is

$$\Delta F_{\text{bind}}=-kT\hspace{0.17em}\text{ln}\left(P_{\text{bound}}/P_{\text{unbound}}\right)$$ (31)

The problem with directly observing these probabilities is that only the most likely probabilities will be adequately sampled, making it hard to determine the entire potential energy function: only the bottoms of potential wells will be accurately determined, and the system will furthermore tend to remain in whatever potential well it started in.

Umbrella sampling is a means of overcoming the difficulty of sampling rare events. Suppose we simulate the system using the actual physical potential U₀ as well as an additional biasing potential U_1, where U₁ is chosen so that the system is forced into a region of configuration space that would otherwise not be seen in simulations. Suppose we wish to measure the thermodynamic average <A(r)>₀ in the unbiased system. We simulate in the biased system. The desired average is then <A exp(βU₁)>₁/<exp(βU₁)>₁ (the subscript 0 or 1 on the angle brackets indicates whether the average is taken in the unbiased or biased system), as we show below:

$$\begin{array}{c}\frac{{\langle A\hspace{0.17em}\exp \left(\beta U_1\right)\rangle }_1}{{\langle \exp \left(\beta U_1\right)\rangle }_1}=\frac{{\displaystyle \int A\hspace{0.17em}\exp \left(\beta {\text{U}}_1\right)\exp \left[-\beta \left(U_0+U_1\right)\right]{\text{d}}^{3N}r}}{{\displaystyle \int \exp \left(\beta {\text{U}}_1\right)\exp \left[-\beta \left(U_0+U_1\right)\right]{\text{d}}^{3N}r}}\\ =\frac{{\displaystyle \int A\hspace{0.17em}\exp \left(-\beta {\text{U}}_0\right){\text{d}}^{3N}r}}{{\displaystyle \int \exp \left(-\beta {\text{U}}_0\right){\text{d}}^{3N}r}}\\ \text{=}{\langle \text{A}\rangle }_0\end{array}$$ (32)

We therefore have obtained a means of unbiasing averages calculated using the biased potential.

Normally, U₁ is chosen to be a harmonic potential for the reaction coordinate z that confines it to be near a fixed value z₀. Then the biased system will sample configurations close to z₀, even when these would not be sampled in the unbiased system. To obtain the potential of mean force, we perform multiple simulations using different values z_0i for the harmonic force center. Each simulation is known as an umbrella window. The mean force, as a function of position, is calculated in each window, and potentials are derived for each window using the unbiasing procedure given above. Because each potential contains an arbitrary constant offset, we then need to glue the potentials together. This is done by a statistical procedure, the weighted histogram analysis method (WHAM) (132) that minimises the discrepancy between each umbrella window, in regions where the windows overlap.

Umbrella sampling is one of the most commonly used means of obtaining potentials of mean force. It has been used to obtain approximate PMFs for large polypeptide toxins unbinding from ion channels. Such computations are, however, still extremely computationally expensive, and convergence to the true PMF over practical computational timescales is uncertain, due to the extreme difficulty of sampling over the full configurational space of the system.

3. History-dependent bias methods

Like umbrella sampling, methods that employ history-dependent bias potentials aim to force the system to sample unlikely regions of the reaction coordinate, rather than simply staying near the local minimum of a potential well. However, while umbrella sampling proceeds by running multiple simulations with fixed and predetermined bias potentials, history-dependent bias methods instead adaptively modify the bias potential of a single simulation such that the system is forced out of potential wells as the simulation progresses. The advantage is that more complicated and abstract reaction coordinates could be easily employed, since, unlike umbrella sampling, there is no need to consider in advance the location and spacing of the umbrella windows or to generate initial configurations for each window.

This strategy was first applied to molecular dynamics simulation in the local elevation method of Huber et al. (112). To force the system out of the most commonly visited macrostates, Gaussian hills are added at discrete locations close to the current reaction coordinate. The height of these potentials depends on how often the current conformation has been visited relative to other conformations. Conformational flooding (101) is a similar idea that aims to speed the rate of transitions between conformational states by “flooding” the local free energy minima with single Gaussian potentials whose parameters depend on the shape of the local minimum. Initially, these methods were proposed as a means of performing a conformational search, but they can be used as a basis by which to calculate PMFs. For example, local elevation umbrella sampling (105) uses the local elevation bias potential as an umbrella potential in a subsequent PMF calculation. Below, we discuss two other commonly used methods; other variations on this idea exist.

Metadynamics (114) is a popular application of history-dependent biasing approach. The system is initially simulated in an unconstrained state, and a dwell histogram is progressively built up over the reaction coordinate. As the system evolves, biasing potentials, in the form of Gaussian potential hills, are applied so as to flatten the potential landscape by filling in the potential wells. Eventually, the biased system is driven to uniformly sample the entire configuration space, at which point the original PMF can be obtained as inverse of the bias potential.

The adaptive biasing force method (61) is another similar method that accumulates the average force system force, rather than occupation probability, in each bin; the bias potential is thus the negative of this average force. The average system force itself corresponds to the gradient of the free energy, and because force is continuous, the free energy can be pieced together using several simulations carried out in nonoverlapping windows.

We are not aware of such methods being used to derive free energies for blocker-channel systems. Such methods should be roughly as effective as umbrella sampling for this purpose, but less sensitive to the choice of parameters (e.g., umbrella spring constants and window spacing are not an issue). One problem is that, unlike umbrella sampling where many windows can easily be run in parallel, the simulation needs to be run as a single serial simulation, unless special steps are taken. For typical blocker channel systems, however, this latter requirement is not really a problem.

4. Potential of mean force via Jarzynski's equality

This computational technique belongs to a different class to the techniques discussed above, as it calculates the free energy from nonequilibrium simulations. Jarzynski's equality is a remarkable equation which states that

$$\Delta F_{A,B}=-kT\hspace{0.17em}\text{ln}{\langle \exp \left[-\beta W_{A,B}\left(x_0\right)\right]\rangle }_A$$ (33)

F_A,B is the free energy difference between states A and B and 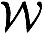_A,B(x₀) is the work performed along the reaction coordinate that takes the system from state A to B along a microscopic trajectory that starts at the coordinates x₀. There is only one such trajectory for each point x₀ because the equations of motion are deterministic. Note, though: the Hamiltonian is often taken to be time dependent. The angle brackets <…>_A denote an averaging over the initial conditions x₀ taken from the macrostate A.

Translating this into the problem of calculating the free energy of binding of a blocker-channel system, we can define a time-dependent Hamiltonian in which the reaction coordinate is pulled from the bound state A to the unbound state B. Typically, this could be done by constraining the center of mass distance between the blocker/channel system using a time-dependent harmonic potential U(z,t) = −(1/2)k[z − z₀(t)]². The distance z₀ could be made to increase more with constant velocity from its initial value towards a value where the blocker is in the bulk. The ensemble of initial conditions may be generated by taking frames from a free simulation of the bound blocker-channel system. For each initial point, the time-dependent pulling potential is applied, and the average above is calculated to derive the free energy between the end points of the path. Various complications arise around the problem of sampling the low probability trajectories, which are given a larger weight in the sum.

The use of this method as a practical means of treating blocker-channel systems was in fact considered by Baştŭg et al. (13), who concluded that, for complex biomolecular systems, umbrella sampling is more efficient.

5. Hybrid FEP/PMF method

The methods that we have discussed above were not specially formulated to deal with the problems of ligand binding and are perhaps more easily applicable to simple situations such as the calculation of the free energy of a single ion. Because blockers are complex molecules, able to undergo conformational change and to orient themselves along any axis, the configurational space that must be sampled to obtain ligand binding PMFs is large, and hence the degree of difficulty involved in accurately determining their binding free energy is much greater. Woo and Roux (256) have proposed a hybrid FEP/PMF method that is designed to overcome some of these difficulties.

The essence of their method is to define a pathway between the bound and unbound states. The blocker is first constrained to its bound orientation and conformation, and to a given axis, while in the binding site, is then pulled out of the binding site along a straight line path, and is finally released from the conformational, orientational, and axial constraints while in the bulk. The authors derive an expression for the binding constant in terms of the free energies associated with the various constraints, as well as a term which involves the potential of mean force of the constrained blocker being pulled out of the binding site, and which does not correspond to a free energy. The free energy terms are calculated using free energy perturbation, and the PMF is calculated using umbrella sampling.

6. Linear interaction energy method

The preceding methods have all attempted, more or less, to calculate the exact value of the free energy from atomistic simulations. The next two methods we shall consider still make use of atomistic simulations, but estimate the free energy based on regression, in the first case, and an approximation of the physics in the second.

The difficulty of the preceding methods is that they require extensive simulations of all intermediate states between the bound state and the unbound state. The linear interaction energy (LIE) method (9) was developed to overcome this computational bottleneck. Two simulations are only performed, one on the bound state and one on the unbound state. Both the van der Waals interaction energy (U_VdW) and the electrostatic interaction energy (U_elec) between the ligand and its environment are averaged for each simulation, and the differences computed. The free energy is then estimated as

$$\Delta F_{\text{bind}}=\alpha \Delta \langle U_{\text{VdW}}\rangle +\beta \Delta \langle U_{\text{elect}}\rangle$$ (34)

where α and β are phenomenological parameters, determined by fitting to known data. The use of the van der Waals interaction energy occurs not because this is the main contributor to the free energy (for example, hydrophobic forces may be more important) but rather because it is an easily computed proxy for the solvent-exposed surface area of the ligand, and therefore varies approximately linearly with other surface area-dependent effects such as the hydrophobic effect.

The linear interaction method appears to offer a reasonable halfway house between the hugely computationally intensive methods discussed above and more approximate or ad hoc methods. There is an issue around the transferability of the parameters α and β between different types of blocker systems; for example, while the standard values may be applicable for small, neutral drug like molecules, a different set of parameters may need to be employed for large, charged polypeptide toxins. Several ion channel blocker studies exist for the case of small ligands (6, 155, 183, 199), but little or nothing has been done for polypeptide blockers or indeed any protein-protein complexes (10).

7. Implicit solvent methods

Moving to a further level of approximation, we shall now consider implicit solvent methods, in which the molecular dynamics simulation is done away with altogether. Such simulations are typically seen in docking applications, where an extremely rapid evaluation of the free energy (or a scoring function that acts as a proxy to the free energy) is required.

As discussed earlier, there are two primary contributions to the free energy: the electrostatic contribution and a nonpolar contribution that consists of van der Waals forces and hydration effects such as the hydrophobic force. The first of these is dealt with by solving the Poisson-Boltzmann equation, often using an approximation such as the generalized Born approximation, and the second is normally dealt with using a surface area-dependent potential. The main point to note is that the free energy can be easily calculated from a single configuration in both cases.

8. Molecular mechanics/Poisson-Boltzmann surface area method

The molecular mechanics/Poisson-Boltzmann surface area (MM/PBSA) method (54, 128, 215) shares some conceptual ideas with the LIE method discussed above. In both methods, atomistic simulations are performed on the bound and unbound systems, and then some approximation is used to calculate the free energy difference between these two states. However, while regression is used for LIE, MM/PBSA instead seeks to apply the sampled conformations of the molecular dynamics simulation to an implicit solvent model (see above) in which the free energy can be more easily calculated. The advantage of this over LIE is supposed to be the fact that fitted parameters (which may not be applicable over the full gamut of ligand/receptor types) are not used; on the other hand, pitfalls in applying continuum electrostatics may lead to other inaccuracies.

The free energy of the bound complex is first decomposed into contributions, which are assumed to be additive.

$$\Delta F=\Delta F_{\text{MM}}+T\Delta S_{\text{MM}}+\Delta F_{\text{PBSA}}+T\Delta S_{\text{MM}}$$ (35)

The bound and unbound systems are simulated using standard (usually explicit solvent) molecular dynamics. The term ΔF_MM, which represents the molecular mechanics bonded energies, is calculated by straightforward averaging over the trajectory. The term TΔS_MM is the entropic contribution to the binding free energy and may be estimated using quasi-harmonic analysis or normal mode analysis. The term ΔF_PBSA represents the contribution to the free energy made by electrostatic and nonpolar nonbonded terms. This term is difficult to derive directly from the molecular dynamics simulations. Instead, representative structures taken from the simulation are evaluated using a continuum model. The electrostatic contribution is calculated by solving the Poisson-Boltzmann equation. The nonpolar contribution is given by the change in the solvent exposed surface area of the ligand, scaled by a fitted constant γ; thus it is not completely true to say that this method is parameter free.

This concludes our general discussion of computational techniques and theory. In the rest of the review, we look at specific examples of computational studies of ion channel block and modulation.

IV. ION CHANNEL PHARMACOLOGY

Various ion channels, such as the voltage-gated K⁺ (Kv) channels (210, 258), the calcium-activated K⁺ (K_Ca) channels (252, 259), voltage-gated Na⁺ (Na_V) channels (68), Ca²⁺ channels (213), and Cl⁻ channels (240), have been shown to be involved in pathology or to act as drug targets. TABLE 1 lists several Kv channels whose malfunction may cause a range of human diseases such as immune disorders and cardiac diseases. The pharmacological and pathological significance of the Kv channels has been reviewed comprehensively elsewhere by Shieh et al. (210) and Wulff et al. (258). Similar to K⁺ channels, Na_V channels are also of high pharmacological importance. For example, several subtypes of Na_V channels including Na_V1.3, Na_V1.7, Na_V1.8, and Na_V1.9 are potential targets of novel analgesics (68, 211). The Na_V1.5 channel, expressed primarily in the heart, may be related to arrhythmias such as long QT syndrome and atrial fibrillation (2). Other less selective ion channels, such as transient receptor potential (TRP) cation channels, have also been shown to be involved in the pathology of various diseases including pain, systemic diseases, aging, and cancer (178). Thus the pathological roles of a variety of ion channels have been discovered.

Table 1.

Pharmacological significance of Kv channels

Subtype	Current	Disease
Kv1.3	IKN	Autoimmune
Kv1.5	IKur	AF
Kv4.3	IKto	Arrhythmia
Kv7.1	IKs	AF, LQTS
Kv7.2	IKM	Epilepsy
Kv10.1	IKdr	Cancer
Kv11.1	IKr	Arrhythmia, cancer

AF, atrial fibrillation; LQTS, long QT syndrome.

V. ION CHANNEL STRUCTURES

The structure of the Kv1.2 channel (40, 151), as illustrated in FIGURE 4, shows that the channel is composed of four identical subunits, with each subunit containing a voltage-sensing domain, a pore domain, and a cytoplasmic domain. The voltage-sensing domain is comprised of four helices S1-S4, which move in response to membrane depolarization and open the channel, while the pore domain contains the S5-S6 helices that form the conduction pathway for ions and the inactivation gate. This voltage-sensing domain does not exist in the bacterial K⁺ channel KcsA (FIGURE 5). Otherwise, KcsA is very similar to the pore domain of Kv1.2. The crystal structure of the bacterial voltage-gated sodium channel Na_VAb is displayed in FIGURE 6A. Na_VAb is also formed by a pore domain and a voltage-sensing domain. The voltage-sensing domain of Na_VAb formed by S1–S4 helices is similar to that of Kv1.2, consistent with the proposal that the general architecture of the voltage-sensing domain is conserved among different channels (35).

Figure 4.

The structure of Kv1.2 (PDB ID 3LUT; Ref. 40) viewed perpendicular to (A) and along (B) the channel axis. The three domains, voltage-sensing domain, pore domain, and cytoplasmic domain, are highlighted in yellow, red, and blue, respectively. In A, the position of membrane is indicated with horizontal bars.

Figure 5.

The structure of KcsA (PDB ID 1BL8; Ref. 71) viewed from the periplasmic side along the channel axis (A) and perpendicular to the channel axis (B). The green spheres represent the K⁺ in the selectivity filter. In A, the four channel subunits are highlighted with different colors. In B, only two channel subunits are shown for clarity.

Figure 6.

The structure of Na_VAb viewed from the periplasmic side along the channel axis (A) and perpendicular to the channel axis (B). In A, the four channel subunits are shown in blue, orange, gray, and red, respectively. In B, the yellow sphere represents a sodium ion.

VI. ION CHANNEL MODULATORS

Numerous molecules, ranging from small ligands to large polypeptide toxins, that occlude the ion-conducting pathway of ion channels (pore blocker), or interfere with the movement of the voltage-sensing domain of voltage-gated ion channels (gating modifier), have been identified. These molecules are useful probes of the structure and function of ion channels, as well as having potential as drugs or drug scaffolds. Knowledge of the detailed mechanisms by which these molecules interfere with channel gating should prove useful for developing novel modulators with lower toxicity and higher efficacy, which may be of clinical use.

To understand the detailed interactions between a channel and its modulators, knowledge of the channel structure is essential. Fortunately, since the first crystal structure of the K⁺ channel KcsA was published in 1998 by Mackinnon and co-workers (71), structures of various cationic channels have been reported, such as the calcium-activated K⁺ channel MthK (117), the voltage-gated K⁺ channel KvAP (118), the voltage-gated K⁺ channel Kv1.2 (151), the Kv2.1-Kv1.2 chimera channel (152), the inward-rectifier K⁺ channels Kir2.2 (228) and Kir3.2 (255), the two-pore domain channels K2P1.1 (166) and K2P4.1 (25), and the voltage-gated Na⁺ channel Na_VAb (187). The available structures of diverse channels have enabled experiments that probe the functional surface of channel modulators and their receptor sites. While the functional surface of the modulators and the location of their receptor sites on channels can be inferred with fair confidence from experimental measurements, the exact binding modes such as the orientation of the toxin upon binding and the modulator-channel interacting residue pairs, which are important for the rational design of novel channel modulators, are only indirectly observable with currently available experimental techniques. Although the interatomic distances inferred from NMR experiments can be used to construct ligand-channel complexes, as demonstrated by Yu et al. (263) and Lange et al. (137), the distances represent ensemble averages and may be misleading if distinct conformations exist. In addition, such experiments suffer from practical difficulties such as the slow tumbling of the large modulator-channel complex in solution and high mobility of transmembrane helices of the channel leading to broadening of proton signals, and thus have not found routine use. Theoretical approaches such as molecular docking and molecular dynamics (MD) simulations, in which the interactions between channels and modulators can be examined in atomic detail, have been used as an aid to experiment. In this section, we look at examples where computational methods have been used to understand the mechanism of action by channel modulators. We will focus on potassium and sodium channels only, whose structures are better understood than other ion channels.

A. Pore Blockers

1. Pore blockers of K⁺ channels

A large number of polypeptide toxins that act on K⁺ channels by occluding the ion conduction pathway have been isolated from venomous creatures such as scorpions, snakes, cone snails, and sea anemones. These toxins, usually containing 30–40 amino acids tightly packed by three or four disulfide bonds, can block the K⁺ current across K⁺ channels with nanomolar or picomolar affinity. Several subtypes of K⁺ channels, such as the voltage-gated K⁺ channel Kv1.3, which is a target for the therapy of autoimmune diseases, have particularly high binding affinities to various polypeptide toxins. Kv1.3 and similar channels exhibit one or several rings of acidic residues lining the wall of the extracellular vestibule. The positively charged toxins, which are abundant in basic residues, are drawn towards the outer vestibular wall of the channel and the entrance of the selectivity filter, where they physically occlude the conducting pathway (137, 138, 185, 263). For example, the NMR structure of the bound complex between charybdotoxin (ChTx) and KcsA (263) reveals that the toxin residue Lys27 wedges into the selectivity filter (FIGURE 7), in line with previous mutagenesis experiments (185). On the other hand, Kv1.5 and Kv4.3 channels carry several basic residues on the outer vestibule, which are repelled by the positively charged toxins. Therefore, Kv1.5 and Kv4.3 are not sensitive to these toxins. For example, charybdotoxin (ChTx), dendrotoxin, and kaliotoxin have been shown to block Kv1.5 with an IC₅₀ of >100 nM, >1 μM, and >1 μM, respectively, compared with the values of 2.6 nM, 250 nM, and 0.65 nM for Kv1.3 (100).

Figure 7.

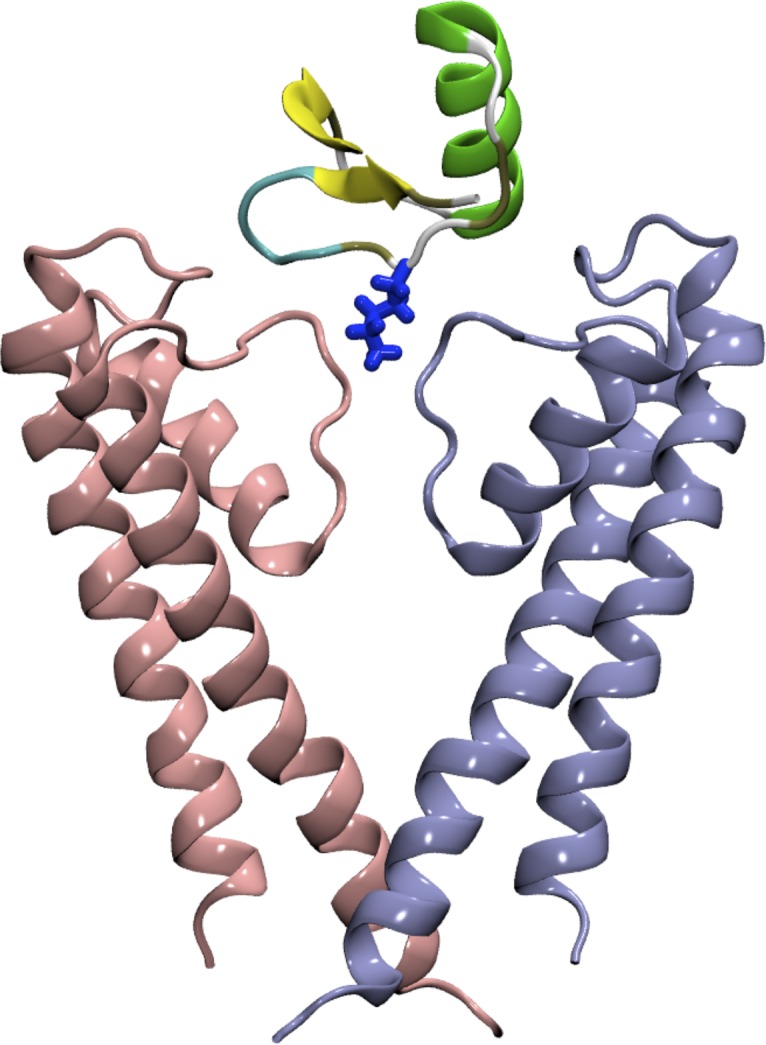
The NMR structure of ChTx in complex with KcsA (PDB ID 2A9H; Ref. 263). The side chain of the Lys27 residue of ChTx which occludes the selectivity filter is highlighted in blue. Two channel subunits are shown in pink and light blue, respectively.

Some of the most well studied toxins are ChTx, margatoxin (MgTx), agitoxin (AgTx), maurotoxin (MTx), α-kaliotoxin (KTx), and ShK which is isolated from a sea anemone. The structures of these toxins are very similar, as illustrated in FIGURE 8. One or two acidic residues are commonly found at the opposite side of the key lysine residue, which occludes the selectivity filter on binding. These acidic residues may be involved in orienting the toxin as it approaches the channel, such that the key lysine residue is pointing to the filter (44).

Figure 8.

The structures of the six polypeptide toxins: AgTx (PDB ID 1AGT; Ref. 130), ChTx (PDB ID 2CRD; Ref. 23), KTx (PDB ID 2UVS; Korukottu et al., unpublished data), MgTx (PDB ID 1MTX; Ref. 120), MTx (PDB ID 1TXM; Ref. 22), and ShK (PDB ID 1ROO; Ref. 236). The side chain of one key lysine residue is highlighted in blue. The side chains of all acidic residues are shown in red. α-Helix is shown in green and β-sheet strand in yellow.

There also exist small K⁺ channel blockers of nonpeptidic nature, such as PAP-1, 4-aminopyridine (4-AP), and tetraethyammonium (TEA). In general, the affinities of these small blockers for K⁺ channels are in the micromolar to millimolar range, significantly lower than that of peptide toxins (104).

Computational studies of ion channel blockers typically involve two steps. First, binding modes of the toxin and channel are predicted, often with the help of existing knowledge from experiment. During this step, different methods, such as Brownian dynamics simulations, molecular docking, and molecular dynamics simulations, with experimental knowledge being used to define restraints, may be used. Then, the predicted binding modes are validated, and unrealistic or incorrect binding modes ruled out. This can be done by calculating experimentally observable quantities such as interaction energies and relative or absolute free energies of the binding modes, which can then be compared with experiment.

Without taking into account any existing knowledge from experiment, it may be possible to use Brownian dynamics simulations to predict toxin-channel interactions. For example, Cui et al. (59, 58) investigated the binding of the scorpion toxin Lq2 to KcsA, and another scorpion toxin P05 to the calcium-activated K⁺ channels of small conductance (SK_Ca). Brownian dynamics calculations were performed to sample the binding modes by each toxin and channel. Subsequently, triplet contact analysis was used to identify the most frequent interacting residue pairs from the Brownian dynamics trajectories. It was found that three arginine residues of P05 form electrostatic interactions with two aspartate residues on the outer vestibular wall of SK_Ca (58, 59). Different binding modes predicted were ranked by calculating the potential energy of each bound toxin due to the electrostatic field created by the channel protein (58, 59). Using similar methodology, Yu et al. (262) examined the binding of six toxins, AgTx2, ChTx, KTx, MgTx, NTx, and Pi2, to Kv1.3. They used Brownian dynamics algorithms to survey the possible binding modes by each toxin and molecular dynamics simulations to measure the structural flexibility of the proteins. It was shown that two basic residues, one lysine and one arginine, of each toxin were in frequent contact with the outer vestibule of the channel, suggesting the important roles of these two residues in binding (262). The potential energies of the toxins due to the electrostatic field of the channel were computed as a measure of the binding affinities. Moderate agreement between the predictions and experiment (correlation coefficient r² = 0.6) was obtained (262), indicating that the binding modes predicted may be reasonable.

Given experimental knowledge of interaction pairs in the bound state, one can use biased molecular dynamics simulations to dock the toxin onto the outer vestibular wall of the channel. For example, in the work by Eriksson and Roux (76), harmonic restraints were applied to maintain the distances between certain toxin-channel residue pairs within certain ranges inferred from mutagenesis experiment. With the restraints applied, the toxin AgTx2, when released in water ∼20 Å from the binding site, was gradually drawn to the outer vestibule of the Shaker (Kv1.0) channel. Depending on the number of restraints applied, four different binding modes were obtained (76). Two of the four binding modes predicted appeared to be unstable in explicit water in unrestrained molecular dynamics simulations, and thus were ruled out. The continuum solvation approximation method was used to calculate the changes in binding free energies due to point mutations of the toxin and channel (76). The binding free energies calculated for the two binding modes agreed equally well with experiment, suggesting that there may be two possible binding modes or the method used was not accurate enough to discriminate between the two binding modes (76). Nevertheless, the two binding modes predicted can be validated by specifically designed experiments (76). Recently, a similar docking method was used by Chen and Chung (46) to examine the binding modes between MTx and three closely related channels, Kv1.1-Kv1.3. A distance restraint was applied between the side-chain nitrogen atom of the Lys23 residue of MTx and the carbonyl groups of a ring of four glycine residues in the selectivity filter. The upper bound of the distance restraint was gradually reduced from 15 to 3 Å, such that the Lys23 residue of MTx was gradually drawn into the channel selectivity filter (46). To verify the robustness of the biased molecular dynamics used as a docking method, each simulation was repeated a second time with different random initial velocities, and a third time with a different toxin orientation at the start of the simulation (46). In addition, the binding mode of MTx to Kv1.2 was also examined using a rigid-body docking method. It was found that the three simulations predict identical binding modes for all the three channels, and the docking calculations of Kv1.2 was in good agreement with the MD simulations. Thus biased molecular dynamics may be used to rapidly predict the binding modes between the toxin and channel, if experimental data are available for at least one distance restraint to be defined.

A third approach to predict toxin-channel binding modes is to combine molecular docking calculations and molecular dynamics simulations. For example, this method has been used by Yi and co-workers (260, 261) and Jin et al. (119) for the blockade of Kv1.2 by MTx and Kv1.3 by ShK, respectively. In all these studies, the docking calculations were used to generate various toxin-channel complexes, which were subjected to cluster analysis. The clustering allowed the distinct binding modes to be identified from the docking calculations. In the case of ShK-Kv1.3, two distinct binding modes were identified (119). Subsequently, molecular dynamics simulations were used to relax the bound complexes in implicit solvent. The MM/PBSA method (128) was applied to derive the change in binding free energy due to point mutation for each binding mode. The predicted relative free energies were compared with experiment, and the binding mode most consistent with experiment was considered as being correct. Alternatively, unrealistic binding modes predicted by docking calculations can be eliminated with available experimental data (42, 44, 45).

Although continuum solvation approximation methods such as MM/PBSA allow the binding free energies to be derived at low computational cost, several difficulties are associated with these methods. For example, the calculations of the enthalpic component of the free energy involve the subtraction of large numbers, resulting in an inherent error in the order of about ±20 kT (127). In addition, the entropic component of free energy is limited to conformational entropy, which cannot be estimated accurately without extensive calculations either (253). In fact, in various previous works such as the ones of Jin et al. (119) and Yi and co-workers (260, 261), the entropic component of free energy was assumed to cancel out between the wild-type and mutant proteins. However, this assumption does not necessarily hold because mutant toxins can have different structural folds (79) and can bind with distinct modes (138). Moreover, the wild-type toxin may bind in alternative binding modes (44). Thus it is desirable to calculate the absolute free energy of binding and directly derive the dissociation constant K_d, which is experimentally observable.

To determine the absolute free energy of binding, the PMF profile as a function of the position of the toxin along a reaction coordinate such as the central channel axis, can be constructed. However, direct sampling of the probabilities of the toxin along the reaction coordinate is impractical with the current molecular dynamics simulation techniques, because of the limited time scale accessible. Thus methods that enhance the sampling of low probability configurations are required for reliable PMF profiles to be constructed (see sect. IIID). The umbrella sampling technique is considered as the most reliable method for constructing the PMF profile for complex ligands such as polypeptide toxins (13).

Chen and Kuyucak (39, 41), starting from the NMR structure of ChTx complexed with KcsA (263), constructed with umbrella sampling techniques the PMF profiles for the dissociation of ChTx from KcsA. Initially, the PMF profile was at a depth of −33 kT, corresponding to an absolute free energy of binding of −28 kT. This value was substantially lower than the value of −14 kT expected from experiment (39). It was found that the structure of the toxin was significantly deformed in bulk (39). The energy associated with the conformational changes of the toxin was estimated to be about −15 kT (39). Once the energy due to the toxin deformation was subtracted from the PMF, the resulting value of −13 kT, corresponding to a K_d value of 2 μM if an R value of 10 Å is assumed in Equation 27, would be in reasonable agreement with the experimental K_d value of 0.9 μM (39). In the subsequent work (41), the toxin structure was maintained rigid with restraints. The PMF profile constructed was in a depth of 19 kT, corresponding to a K_d value of ∼0.9 μM assuming a R value of 0.7 Å in Equation 27. Although it is unclear why two vastly different R values (10 and 0.7 Å) have been used by Chen and Kuyucak (39, 41), their work demonstrates that in principle it is possible to construct reliable PMF profiles for the dissociation of the toxin from the binding site, with molecular dynamics simulations and umbrella sampling. Similar techniques have been used by Khabiri et al. (124), Chen and co-workers (42, 44), and Gordon and co-workers (93, 94).

Recently, Chen et al. (42) have applied a molecular docking method, molecular dynamics simulations, and umbrella sampling to understand the structural basis of the binding of three toxins, ChTx, ShK, and OSK1, to Kv1.3. A crude binding mode between each toxin and Kv1.3 was selected from various poses generated by rigid body docking. Experimental data were taken into account in selecting the binding modes; the residue Lys27 of ChTx and OSK1, and Lys22 of ShK were assumed to enter the selectivity filter (42). Each crude binding mode was then allowed to evolve to a low energy state with molecular dynamics simulations in the absence of any restraints, allowing favorable binding interactions to be formed (42). The binding modes revealed that all three toxins form two strong electrostatic interactions with the channel, one in the entrance of the selectivity filter and the other at the outer vestibular wall (42). The binding mode of OSK1 to Kv1.3 is shown in FIGURE 9A as an example. In addition, the longest principal axis (FIGURE 9B), and not the dipole moment of the toxins, was aligned with the channel permeation pathway in the bound states (42). With the use of umbrella sampling, the PMF profiles for the unbinding of the three toxins from Kv1.3 were constructed (FIGURE 9C). The dissociation constants K_d of toxin unbinding calculated were 25 nM for ChTx, 0.17 nM for ShK, and 0.02 nM for OSK1. The K_d values determined experimentally are 0.71–2.6 nM for ChTx (3, 100), 0.011–0.133 nM for ShK (123, 188), and 0.014 nM for OSK1 (171). Therefore, the K_d values calculated for the three toxins were within one order of magnitude of experimental values, suggesting that the binding modes predicted are of reasonable quality (42).

Figure 9.

A: the position of OSK1 relative to the Kv1.3 channel predicted from docking and molecular dynamics simulation (42). The backbones of the basic, acidic, and other residues of OSK1 are shown in blue, red, and green, respectively. The side chains of OSK1 residues that protrude into the channel selectivity filter (Lys27) or form salt bridges (Arg24) with the channel are highlighted in blue. Two channel subunits are shown in gray. The carbonyl groups of the channel residues forming the selectivity filter are highlighted in red. The side chain of the channel acidic residue (Asp433) that forms salt bridges with the toxin is highlighted in red. Toxin residues are labeled in blue and channel residues in black. B: the principal axes (yellow arrows) and the dipole moment (red arrow) of OSK1. The sizes of the toxin along the longest and shortest axes are given. C: the PMF profile for the unbinding of OSK1 from Kv1.3 along the channel axis (z). [Modified from Chen et al. (42), with permission from Elsevier.]

In conclusion, the studies mentioned above have shown promises in predicting the absolute binding free energy and K_d for the toxin blockers with computational methods. Such calculations allow the predicted binding modes to be directly validated against experiment. In the view of the authors, computational methods will play growing importance in understanding the mechanisms of action by pore blockers of K⁺ channels.

2. Pore blockers of Na⁺ channels

Voltage-gated sodium channels (Na_V), responsible for the rising phase of action potential, are widely distributed in muscle and neuronal cells (33). In addition to mammals, Na_V channels have also been discovered in bacteria (126, 203). Bacterial Na_V channels are homo-tetramers; each monomer is comprised of six transmembrane helices (S1–S6), as revealed by the crystal structure of the Na_V channel from Arcobacter butzleri (Na_VAb) (187). The four helices S1–S4 form the voltage-sensing domain, whereas the S5–S6 helices form the pore domain that lines the ion permeation pathway. Mammalian Na_V channels, on the other hand, are integral proteins containing four nonidentical subunits.

Neurotoxins bind to different receptor sites on Na_V channels and interfere with the gating mechanism (217). The receptor site 1, formed by the selectivity filter and the outer vestibular wall, provides the binding site for two classes of toxins, guanidinium toxins and μ-conotoxins. Once bound, these pore blocker toxins are believed to physically occlude the ion permeation pathway. Two widely recognized guanidinium toxins, tetrodotoxin (TTX) and saxitoxin (STX), are illustrated in FIGURE 10. Both TTX and STX carry one or two guanidinium groups. In contrast to guanidinium toxins, which are relatively small molecules compared with the size of one or two amino acids, μ-conotoxins are polypeptides containing typically 22–25 amino acids (229). The backbone of μ-conotoxins is stabilized by three disulfide bridges and therefore very rigid. This rigid backbone may be important for maintaining the functional surface of μ-conotoxins.

Figure 10.

Chemical structure of the cationic forms of TTX and STX.

Due to the unavailability of the crystal structure of mammalian Na_V channels, which is required for reliable results to be derived from structured-based theoretical methods such as molecular docking, Brownian dynamics, and molecular dynamics simulations, much of the computational work on the binding of pore blocker toxins to Na_V channels has been focused on homology modeling and molecular docking. Typically, the crystal structure of a potassium channel such as KcsA (71) and MthK (117) is used for generating a model of a Na_V channel (147, 148, 232). Despite the fact that the homology models of the Na_V channels were generated based on the assumption that the selectivity filter of Na_V channels is similar to that of Kv channels, such models allowed some molecular docking (147), Monte Carlo sampling (232), and molecular dynamics simulations (162) to be performed. Several models for the mechanism and binding modes of TTX and STX (147, 232) and μ-conotoxins (162) to Na_V channels have been proposed. However, the exact binding modes between these blockers and Na_V channels have yet to be elucidated.

In 2011, the first crystal structure of Na_V channels, Na_VAb (187), was reported. Although the structure of Na_VAb shares many features with potassium channels such as KcsA (71) and MthK (117), there are also significant differences, especially in the selectivity filter region. For example, the diameter of the selectivity filter of Na_VAb is 5 Å, ∼2 Å wider than that of potassium channels. This highlights the fact that the binding modes of the Na_V channel blockers predicted using homology models based on the structure of potassium channels need to be reassessed.

The crystal structure of Na_VAb provides a structural basis for understanding the mechanism of action by Na⁺ channel blockers, such as TTX, STX, and μ-conotoxins. Although Na_VAb is resistant to TTX (203), it has been demonstrated that the channel is inhibited by a subtype of μ-conotoxins, PIIIA (44). The selectivity filter includes a ring of glutamate residues (E177), and a ring of glutamate residues (E189) is located on the outer vestibule of the channel (see FIGURE 11A). With the use of molecular dynamics simulations, it was found that the positively charged toxin PIIIA, released in water 15 Å above the binding site, spontaneously bound to the channel outer vestibular wall and occluded the ion permeation pathway with the side chain of either a lysine or an arginine residue (FIGURE 11B), indicating that PIIIA is capable of inhibiting Na_VAb (44). The results also indicated that PIIIA may block Na_VAb with multiple binding modes, which was confirmed by free energy calculations (44). The free energy calculations showed that different binding modes share similar free energies of binding, suggesting that the binding modes are equally probable. This interpretation was also confirmed experimentally by Stevens et al. (218). Thus certain toxins may block Na_V channels with alternative binding modes, rather than the single binding mode generally assumed.

Figure 11.

A: structure of the pore domain of the NaVAb channel, viewed perpendicular to the channel axis. Only two subunits are shown for clarity. B: PIIIA blocks the ion conduction pathway of the Na_VAb channel with the side chain of the residue Arg2. Green ribbon represents the toxin backbone, and the yellow sphere represents a sodium ion. [From Chen and Chung (44), with permission from Elsevier.]

In addition to TTX, STX, and μ-conotoxins, drug molecules like local anesthetics may also act as pore blockers of Na_V channels. The receptor site of local anesthetics has been shown to be in the inner vestibule (177), rather than the outer vestibule for μ-conotoxins. Recent docking calculations suggest that local anesthetics may block the current by creating a positive electrostatic field in the inner vestibule, which repels cations (148).

B. Gating Modifiers

1. Gating modifiers of K⁺ channels

A number of polypeptide toxins that interfere with the gating mechanism of voltage-gated K⁺ (Kv) channels have been isolated from spider venoms. These tarantula toxins bind to the voltage-sensing domain of Kv channels within the membrane and hinder the conformational changes that occur during channel opening (141, 165, 164, 220). Once the voltage-sensing domain is bound with toxins, a stronger depolarization is required to activate the channel, thus shifting the activation-voltage curve to the right (220).

Tarantula toxins are typically of 25–40 amino acids in length. The structure of tarantula toxins is rigid, as the toxin backbones are cross-linked by three or four disulfide bonds forming the inhibitor cysteine knot motif, which is also commonly found in pore-blockers (180). Some of the most well-characterized tarantula toxins are hanatoxin (HaTx) (221), Scodra griseipes toxin (SGTx1) (160), heteropodatoxin (HpTx) (207), phrixotoxin (PaTx) (69), and the voltage sensor toxin (VSTx) (205). The solution structure of these toxins suggests that a hydrophobic surface is conserved across tarantula toxins (225, 121, 140), although the size and shape of this surface varies. The critical role of this hydrophobic surface in toxin function has been demonstrated experimentally (165, 220, 245). The toxins may use this hydrophobic patch to interact with the voltage-sensing domain. Once bound to the voltage-sensing domain, they may stabilize it in the closed conformation so that the channel is harder to open. The functional surface of tarantula toxins on the voltage-sensing domain of Kv channels has been examined extensively with mutagenesis techniques (64, 65, 145, 146, 191, 222, 223, 264). These showed that the periplasmic half of the S3 helix forms part of the receptor site. However, the exact binding modes by tarantula toxins have not been resolved by experiments.

To date, most molecular dynamics simulations have been concerned with the energetics associated with partitioning tarantula toxins into membranes. For example, using atomistic molecular dynamics simulations, Bemporad et al. (17) examined the preferred location of VSTx1 within lipid membranes. The simulations showed that VSTx1, when placed within the hydrophobic core or the aqueous phase, spontaneously moves to the surface region containing the lipid headgroups. When bound to the surface region, about half of the toxin remains buried within the hydrophobic core of the lipid bilayer, whereas the other half is interacting with the head groups of lipids (17). Contrastingly, in the work of Nishizawa and Nishizawa (179), HaTx1 was observed to penetrate deeply to near the center of the bilayer, but not to form a stable complex with the bilayer when bound to the surface region. In subsequent studies, the PMF profiles of VSTx1 along the bilayer normal reveal that the preferred binding location of VSTx1 is ∼20 Å from the center of a lipid bilayer (248, 250). Thus all the simulations illustrated here are in support of the earlier proposal which states that tarantula toxins bind to the voltage-sensing domain within membranes. Molecular dynamics simulations have also been used to understand the binding modes between VSTx1 and the isolated voltage-sensing domain of K_VAP (249). VSTx1, which is in the water phase at the simulation start, spontaneously binds to the voltage-sensing domain of K_VAP in multiple coarse-grained simulations each on a time scale of 3 μs (249). The receptor site on the voltage-sensing domain was found to be primarily formed by residues from the S1 and S4 helices (249).

2. Gating modifiers of Na⁺ channels

Eukaryotic Na_V channels are integral proteins consisting of four homologous subunits (I–IV); each subunit contains a voltage-sensing domain and a pore domain. A large number of polypeptides isolated from venoms of scorpions, spiders, and sea anemones have been shown to interfere with the gating mechanism of Na_V channels (32, 217). For example, scorpion α-toxins bind to the periplasmic side of the voltage-sensing domain of the subunit IV and slow or inhibit channel inactivation (96). Scorpion β-toxins, on the other hand, bind to the voltage-sensing domain of the subunit II, trap the voltage-sensing domain in an outward position, resulting in the channel to open at less depolarized voltages (103). Scorpion α- and β-toxins are typically of 60–80 residues in length and have rigid backbone cross-linked by four disulfide bridges (195). Although α- and β-toxins have distinct functional effects on Na_V channels, their shape and secondary structure are rather similar, as illustrated in FIGURE 12. As scorpion α- and β-toxins are believed to be potential leads for developing novel insecticides (96, 103), numerous experiments have been carried out to understand their functional surface and binding modes to Na_V channels. However, despite the fact that several models have been constructed with molecular docking methods for the bindings of the α-toxin LqhII (247) and the β-toxin Css4 to Na_V1.2 (34, 265), the binding modes of scorpion α- and β-toxins to Na_V channels have not been fully resolved by experiments. In addition to scorpion α-toxins, various δ-conotoxins isolated from marine cone snails have also been shown to inhibit the fast inactivation of Na_V channels (14, 78, 254). The receptor site of δ-conotoxins overlaps with that of scorpion α-toxins (142), suggesting that the two families of toxins may inhibit channel inactivation with similar mechanisms.

Figure 12.

The secondary structure of two α-toxins, AahII (107) and LqhαIT (237) (A), and two β-toxins, Css4 and Cn2 (194) (B). The structure of Css4 is modeled on Cn2. The two toxins are 83% identical in sequence. Helices are shown in purple, β-sheet strands in yellow, and others in gray. The side chains of residues at positions 8, 18, and 64 are highlighted. Basic residues are colored in blue, acidic in red, and others in green. [Modified from Chen and Chung (48).]

Using a molecular docking method and molecular dynamics simulations, Chen and Chung (47) have examined in detail the binding of two β-toxins, Css4 and Cn2, to the isolated II voltage-sensing domains of rat Na_V1.2 and rat Na_V1.6, respectively. Experimentally, Css4 has been shown to interfere with the gating mechanisms of both Na_V1.2 and Na_V1.6, whereas Cn2 selectively targets Na_V1.6 (208), at nanomolar toxin concentrations. Yet, Css4 and Cn2 share a sequence identity of 83%, being significantly different at only three positions, 7, 8, and 64, which are in spatial proximity due to the disulfide bridge between Cys12-Cys65. As the difference in these three residues apparently gives rise to the distinct sensitivity of Css4 and Cn2 to Na_V channels, it is likely that they are involved in binding (208). Following the assumption that residues 7, 8, and 64 form part of the functional surface, a docking method was used to search for a plausible binding mode between Css4-Na_V1.2 and Cn2-Na_V1.6 (47). For each toxin-channel pair, a unique structure that is consistent with the assumption was selected out of 300 docking poses. Each selected structure was then embedded in a lipid bilayer and a box of explicit water, and run for 20 ns with molecular dynamics simulations without the presence of any restraints, allowing the complex to evolve to a stable state in a membrane-like environment. The toxin-channel interacting residue pairs were identified and validated by comparing with mutagenesis experiments and previous models (47). The K_d values derived with umbrella sampling were 20 nM for Css4 and 70 nM for Cn2, which were in reasonable agreement with the experimental values of 1 and 40 nM, respectively (47). The simulations revealed that both Css4 and Cn2 wedge into the receptor site with a loop between positions 8 and 18 (FIG. 13, A AND B), which is referred to as the Linker domain (47). In this loop, two charged residues, Lys13 and Glu15, are commonly found in anti-mammalian β-toxins. These two charged residues and a critical glutamate residue (Glu28) were observed to form hydrogen bonds and salt-bridges with the receptor site (FIGURE 13C), stabilizing the toxin-channel complex. Thus the simulations suggest that the functional surface of anti-mammalian β-toxins is conserved, centered on the Linker domain (47). Interestingly, the crystal structure of Cn2 bound to its antibody also shows that the Linker domain plays a central role in the binding (29).

Figure 13.

A: the position of Css4 bound to the IIS1-S4 voltage-sensing domain of Na_V1.2, relative to the lipid bilayer. The surface of the voltage-sensing domain is shown in transparent silver. Toxin backbone is in yellow. Horizontal lines indicate the average position of the phosphate groups of the lipids. The loop between positions 8 and 18 of the toxin is highlighted in red. B: Css4 bound to the voltage-sensing domain of Na_V1.2. The side chains of two key residues of the toxin, Lys13 (blue) and Glu15 (red), are highlighted. The S2 and S4 helices of Na_V1.2 are highlighted in pink and lime, respectively. C: Css4 bound to the voltage-sensing domain of Na_V1.2 showing three of the key contacts. Toxin backbone is shown in yellow. The complexes shown in B and C are rotated by ∼90° counterclockwise from that of A. [From Chen and Chung (47).]

The functional surface of β-toxins uncovered by Chen and Chung (47) appears to overlap with the functional surface of α-toxins determined experimentally, consisting of the NC-domain around residues 7, 8, and 64, and the Core domain around the residue 18. These two domains are interconnected by the Linker domain, which wedges into the receptor site in β-toxins. Given the similarity between the structure of α- and β-toxins, it seems that the functional surface may be conserved not only in β-toxins, but also between α- and β-toxins. Following this assumption, Chen and Chung used molecular dynamics simulations with distance restraints as a docking method to examine the binding of two α-toxins, the anti-mammalian toxin AahII, and the anti-insect toxin LqhαIT, to the IV voltage-sensing domain of rat Na_V1.2 (48). The distance restraints were determined assuming that the Linker domain of the two α-toxins wedge into the receptor site in a similar orientation to that of β-toxins. With the distance restraints applied, the toxins were drawn to the receptor site rapidly within a few nanoseconds. It was found that both AahII and LqhαIT were able to form several favorable electrostatic and hydrophobic interactions with the receptor site, demonstrating that toxin-channel complex is stable with the Linker domain wedging into the binding groove. The K_d values derived were 17 nM for AahII and 1 μM for LqhαIT, which agree well with experiment which shows that AahII is about three orders of magnitude more potent than LqhαIT for Na_V1.2 (122). Computational mutagenesis calculations were performed on two channel mutants (48), E1551R and R1626E. Experimentally, these two mutations did not have any measurable effects on toxin binding affinities (247). However, both E1551 and R1626 were observed to form salt bridges with the toxin in the models, which casts doubts on the consistency between the models and experiment. The computational mutagenesis calculations eliminated this doubt. It was found that AahII was able to form an equivalent salt bridge when the one due to E1551 or R1626 was broken due to the mutation, such that each of the mutations did not change the binding affinity of AahII significantly. For example, the K_d value calculated for the E1551R mutant channel compared favorably with that of the wild type (48). This highlights the importance of interpreting mutagenesis data with caution. In support of the binding modes predicted for AahII-Na_V1.2, the δ-conotoxin EVIA was observed to bind to the VS domain of Na_V1.2 spontaneously in 50 ns, forming similar salt bridges as that observed in the AahII-Na_V1.2 complex (48).

In conclusion, the computational studies of Chen and Chung (47, 48) demonstrated the key role of the Linker domain in the binding of α- and β-toxins to Na_V channels. In all the models of α- and β-toxins bound to Na_V channels predicted (47, 48), at least one salt bridge between the toxin and the S4 helix of the VS domain was observed. It remains to be elucidated whether or not such a salt bridge is vital for the action of the toxins.

VII. FUTURE PROSPECTS

We have first outlined some theoretical principles underlying state-of-the-art computational tools currently being used for studying biological macromolecules. We then summarized some of the salient features uncovered using computational methods of the actions of channel blockers, concentrating on polypeptide toxins extracted from venomous animals, on voltage-gated cationic channels. In the future, computational modeling of ligand-channel interactions may play a prominent role, providing physical explanations of the mechanisms underlying modulations of channel properties by large polypeptides and intermediate-sized drug molecules. For example, detailed knowledge of the bioactive conformations of polypeptide toxins to specific channel subtypes may lead to a host of novel pharmaceutical products.

In theory, one should be able to gain important knowledge of ligand-channel interactions using computational techniques. For example, in silico studies should enable us to identify the ligand binding site, reveal pairs of interacting ligand-channel residues, and determine the binding affinity. Many efficient algorithms and computational tools have been devised over the past decades, designed to unveil the modes of interactions between macromolecules. Undoubtedly, these tools will be further refined and improved, such that they will rapidly provide insights into how small or large molecules modulate the conductance properties of biological ion channels.

To date, computational studies of blocker-channel interactions mainly rely on two-step procedures. First, with the use of molecular docking programs, Brownian dynamics, or biased molecular dynamics simulations, a toxin is complexed to the external vestibule or the voltage-sensor of a specific channel. If a docking program is used for this step, one or two docking poses among a large number of possible poses generated by the program are selected based on prior experimental knowledge. Many state of the art docking programs do not currently appear to be accurate enough to routinely derive correctly docked bound states of polypeptide toxins on ion channels without a degree of operator input and prior knowledge. This would be a problem for a truly high-throughput screening and ranking system, which in any case we believe is some way away. When experimental information is available, this can be incorporated into the docking procedure using distance restraints (43). Biased molecular dynamics also works well for this purpose (46, 48). Toxin pore blockers, which block the channel by inserting a lysine or arginine residue into the pore, are an easier case, because each toxin has only a small number of such residues available to be inserted into the pore, and inserting a residue into the pore vastly constrains the number of available poses. Thus, in these cases, the problem appears to simply be one of finding the correct protocol and tools rather than a deficiency in current algorithms.

Following the generation and selection of docked poses, the free energy of binding and binding affinity, which are experimentally observable quantities, may be calculated. Also, the bioactive surface of a specific toxin can be identified by examining the residue pairs forming hydrogen bonds in the toxin-channel complex. Moreover, it is possible to carry out theoretical site-directed mutagenesis to enhance its sensitivity and selectivity (45, 123) or prune the molecule to render it smaller and more durable (52, 63, 125). In recent studies, the K_d values derived using the umbrella sampling technique and explicit representation of water appear to be within one to two orders of magnitude of that measured experimentally in various toxin-channel systems (41, 42, 46, 94, 200). These approaches, however, cannot be routinely used to search for lead candidates of channel blockers from large numbers of available compounds, because of prohibitively high computational costs. Typically, it takes between 50,000 and 75,000 CPU hours of a modern supercomputer to construct a profile of potential of mean force of one toxin, using molecular dynamics umbrella sampling methods with simulation times that are barely sufficient. As discussed in the review, other, approximate, free energy methods are available, but it is harder to assess their accuracy in predicting the binding affinity of toxins to ion channels, due to a lack of computational studies. The LIE method did not work well in predicting the relative binding affinities of MTx to Kv1.1, Kv1.2, and Kv1.3 in one study (46), possibly because the entropic component of the free energy which is ignored by the method cannot be cancelled out between the channels. The MM-PBSA method, on the other hand, appears to offer a plausible means of calculating the changes in free energy due to a single mutation to the toxin (119, 260, 261). But clearly more work needs to be done to achieve a more generally applicable methodology.

It will therefore be desirable to devise a computational algorithm, either an improved version of molecular docking programs, a more sophisticated Brownian dynamics technique incorporating the flexibility of ligands and channels, or a clever modification and specialization of standard molecular dynamics, that can rapidly determine the binding mode between the ligand and the channel and accurately calculate the free energy of the binding. Such an algorithm might have the following features, all of which are found in various existing programs and techniques but which will need to be further synthesized and improved.

Implicit water, and possibly lipids, will probably be needed. Modeling all of the water molecules in the assembly takes us into the realms of standard molecular dynamics, which is too slow for our desired purpose. Note that not all the water needs to be implicit. Explicit water could in principle be employed around the channel pore and blocker, with implicit water being used further away.

Large portions of the simulation assembly could be fixed, treated using rigid body approaches or otherwise treated in a simplified manner. The purpose is again to increase computational efficiency. It is probably too ambitious to take an approach where all possibilities of large-scale conformational change are taken into account. Instead, the conformations of large parts of the channel and blocker should be taken to be invariant, thus allowing fixing to take place.

The long-range electrostatics should be reasonable. This is particularly important for ion channel blockers that bind in the pore. Such blockers are usually highly charged and are attracted to the oppositely charged outer vestibule of the channel by long-range electrostatic forces that contribute a significant portion of the total binding affinity. The channel pore itself is a region where strong, highly focused electric fields are present, and thus getting the electrostatics right in this region may be important.

Hydrogen bonding and salt bridges need to be correctly dealt with. These short range forces contribute a large percentage of the binding affinity of typical ion channel modulator toxins.

Nonpolar hydration forces, such as the hydrophobic force, need to also be reasonably well modeled, because these forces are also important to binding.

Flexibility should be taken into account. We have spoken above about fixing parts of the system. When protein toxins bind to an ion channel, we would require that the residues involved in key contacts be able to attain the necessary geometric configuration. We would also require, where necessary, that the selectivity filter of the channel should be flexible enough to allow basic side chains to be inserted into the filter, as is seen in many ion channel blocker toxins.

Implicit water, lipids, and the fixing of the interior of the protein and lipid regions necessitate the use of some kind of macroscopic electrostatics treatment. We have discussed various approaches to macroscopic electrostatics in the earlier sections of this review. Presolving Poisson's equation or the Poisson-Boltzmann equation and then storing the results in lookup tables is an extremely fast approach often taken by Brownian dynamics and docking programs. Approximations are necessary to deal with the interactions between two or more molecules or ions in such an approach, due to considerations of dimensionality of the lookup tables. Generalized Born electrostatics are able to deal with nonrigid bodies, and are also able to deal with all interactions between simulation bodies, but are slower and potentially less accurate. A combination of the two might be worth trying. If explicit water were to be employed only inside the channel and around the binding interface, then it might be possible to get away with a very fast and simplified version of macroscopic electrostatics.

The treatment of hydrogen bonding and salt bridges is also difficult. Hydrogen bonds exist as a delicate balance between attractive Coulomb forces involving small, mobile hydrogen atoms, repulsive steric forces, attractive dispersive forces due to the van der Waals potential, and the mediating influence of the surrounding solvent. Atomistic molecular mechanics often deal with this by explicitly modeling all elements of the above, using a carefully calibrated parametrization. Changing any of the elements, for example, fixing hydrogens or combining them with parent atoms or using an implicit solvent force field, will seriously disrupt this delicate balance. It seems likely that either of two approaches might be taken. The first approach models the binding interface and other important parts of the system using fully atomistic, explicit solvent molecular dynamics while retaining more approximate representations in more distant regions. The second approach introduces special empirical forces for hydrogen bonding and salt bridges. The latter treatment is common in docking programs.

The treatment of nonpolar forces faces problems similar to that of hydrogen bonds. Implicit solvent force fields often rely on a surface area-based approach, where the nonpolar energy of a group of one or more molecules scales with the solvent accessible surface area. Scaling constants are parametrized based on the calculated solvation free energies of libraries of molecules. There is some danger that the parameterizations may not lead to accurate binding forces due to the simplified nature of the model. More sophisticated treatments exist, but at the time of writing it is hard to pick a clear winner. Again, the approach of including explicit water molecules around the binding region may help to ameliorate the problems.

In general, state-of-the-art implicit solvent force fields seem to be able to predict the solvation energies of biomolecules to within several kcal/mol (115, 139). Careful parameterizations (38) seem to be able to derive potentials of mean force for small molecular fragments that have a comparable error scale. Ideally, we would like to be able to compare and rank the binding free energies of similar toxins, where an accuracy of a few kilocalories per mole might still give useful information. Therefore, it appears that current algorithms are probably somewhere on the cusp of success versus failure in this regard. A good treatment of solvation will therefore be a critical part of any new tool.

The other critical requirement is flexibility, which was discussed in the sections on Brownian dynamics and docking. While flexible side chains and a limited degree of flexibility in the channel can be designed into computational tools without incurring too much overhead, there are areas, such as the treatment of unordered turret loops in the outer vestibules of ion channels, that are inherently hard to deal with, and will probably remain so for some time. Results might therefore need to be interpreted carefully in the light of these kinds of uncertainties.

The discussion above tends to view the problem from a physical perspective, referring as it does to various types of physical forces. It will also be interesting to see how more abstract force fields, based on machine learning, such as that used in Autodock Vina (234) will perform in the future, and whether such approaches will prove useful for studying channel-toxin binding.

Thus there are difficult, but surely not insurmountable, problems to be overcome. The authors of this review are involved in investigating the use of Brownian dynamics to study ion channel modulator systems. Our system employs a fixed channel, lookup-based electrostatics, and blocker molecules that consist of coupled rigid bodies. Phenomenological pair potentials are used for hydrogen bonding, salt bridges, and also for modeling hydrophobic forces. The calibration of the parameters of the model is in general difficult, largely because the parameters tend to have a high degree of interdependence. The calibration methodology will therefore need a good deal of thought and research. We believe that it might be worthwhile to develop a set of specialized parameters aimed squarely at ion channels and toxin blockers. We are hopeful that this approach might allow a program that is accurate enough to predict binding modes of toxins and can correctly rank different toxins or mutations of toxins. This kind of specialized approach would also be worth investigating from the point of view of developing existing molecular dynamics free energy techniques, such as LIE or MM-PBSA. Even a very specialized, but fast and accurate, methodology would find important clinical applications.

There are numerous polypeptide toxins yet to be discovered and characterized from venoms of arachnids, reptiles, and marine invertebrates. For example, it has been estimated that there are 500 Conus species, each of which has ∼100 different conotoxins (230). Only a handful of conotoxins to date have been characterized and tested. The advent of a new, powerful algorithm will enable us to rule out rapidly a very large number of untested toxins with inferior blocking characteristics so that in vitro or in vivo experimental testing can be more focused. These approaches will also render computational and theoretical approaches to be useful for the design of modern drugs targeting biological ion channels.

GRANTS

This work is supported by grants from the National Health and Medical Research Council and the MAWA Trust.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.