Fig. 4.

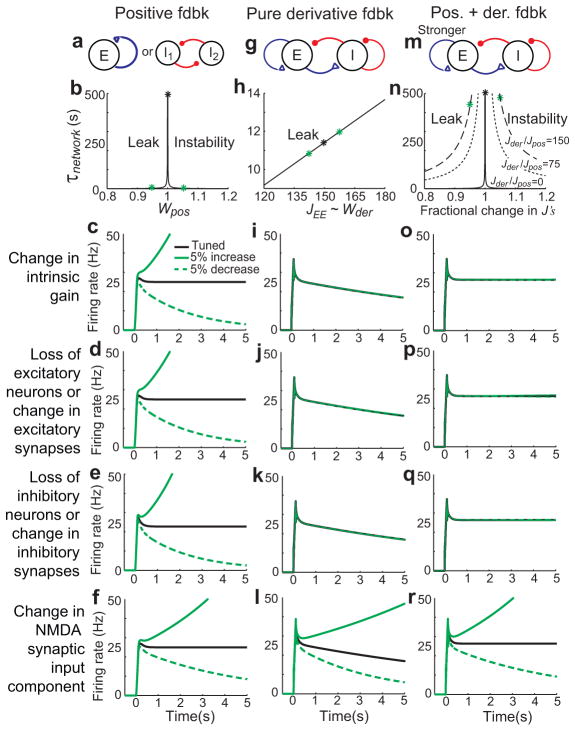
Robustness to common perturbations in memory networks with derivative feedback. a–f, Non-robustness of persistent activity in positive feedback models. a, Positive feedback models with recurrent excitatory (left) or disinhibitory (right) feedback loops. b, Effective time constant of network activity, τ_network, as a function of connectivity strength. Green asterisks correspond to 5% deviations from perfect tuning. c–f, Time course of activity in perfectly tuned networks (black) and following small perturbations of intrinsic neuronal gains (c) or synaptic connection strengths (d–f). g–k, Robust persistent firing in derivative feedback models. To clearly distinguish the hybrid models with derivative and positive feedback, purely negative-derivative feedback models with no positive feedback are shown. All excitatory synapses are mediated by both NMDA and AMPA receptors as in Fig. 3, with parameters chosen to coincide with experimental observations [13]. h, τ_network increases linearly with the strength of recurrent feedback J. i–k, Robustness to 5% changes (green asterisks in h) in neuronal gains or synaptic connection strengths. l, Disruption of persistent activity in derivative feedback models following perturbations of NMDA-mediated synaptic currents. m, Hybrid model with positive and derivative feedback. n–q, As the strength of negative-derivative feedback is increased, τ_network decreases less rapidly with mistuning than in purely positive feedback models (n) and the network becomes robust against perturbations (o–q, shown for J_der/J_pos=150). r, Disruption of persistent activity in the hybrid model following perturbations of NMDA-mediated currents.