Functional characteristics of a double negative feedback loop mediated by microRNAs

Abstract

MicroRNAs (miRNAs) are a class of small, noncoding RNAs that play crucial roles in almost all cellular processes. As key post-transcriptional regulators of gene expression, miRNAs mainly induce mRNA degradation or translational repression. Recently computational and experimental studies have identified an abundance of motifs involving miRNAs and transcriptional factors (TFs). Here, we study the functional characteristics of one such motif, a two-node miRNA-mediated double negative feedback loop (MDNFL) in which a TF suppresses an miRNA and the TF itself is negatively regulated by the miRNA. Several examples of this motif are described from the literature. We propose a general computational model for the MDNFL based on biochemical regulations and explore its dynamics by using bifurcation analysis. Our results show that the MDNFL can behave as a bistable switch. This functional feature is in agreement with experimental observations of the widespread appearance of miRNAs in fate decisions such as differentiation during development. Importantly, it is found that under the interplay of a TF and an miRNA, the MDNFL model can behave as switches for wide ranges of parameters even without cooperative binding of the TF. In addition, we also investigate how extrinsic noise affects dynamic behavior of the MDNFL. Interestingly, it is found that when the MDNFL is in the bistable region, by choosing the appropriate extrinsic noise source, the MDNFL system can switch from one steady state to the other and meanwhile the production of either miRNA or protein is amplified significantly. From an engineering perspective, this noise-based switch and amplifier for gene expression is very easy to control. It is hoped that the results presented here would provide a new insight on how gene expression is regulated by miRNAs and further guidance for experiments.

Introduction

Living cells can continuously react to their environment with specific biochemical responses. At the core of this functionality are the interaction networks of biochemical molecules, such as genes, proteins, metabolites, and small molecules. Over the past decade, the structures of a great deal of such networks, including protein–protein interaction, metabolic, signaling, and transcription regulatory networks, have been mapped out. For the transcriptional regulation networks and protein–protein interaction networks of different organisms, large-scale statistical analysis has uncovered that these networks are far from random and contain significantly recurring nontrivial patterns of interconnections termed network motifs, such as negative autoregulation, feed-forward loops, and feedback loops (Shen-Orr et al. 2002; Lee 2002; Wuchty et al. 2003). In addition, several motifs of mixed interaction, including two types of interactions: those between transcription factors and their target genes and those between proteins, have also recently been found in integrated cellular networks of transcription regulation and protein–protein interactions (Yeger-Lotem and Margalit 2003; Yeger-Lotem et al. 2004). Understanding the functionality of these network motifs can help elucidate the design principle and provide insight into the behavior of regulatory networks. Previous work in transcriptional regulatory networks of several species has discovered that each motif has a specified structure and capacity to perform specific information-processing functions (Alon 2007).

Gene expression is under tight regulation at many levels (Shimoni et al. 2007). In the past, it was widely recognized that the regulation of gene expression is a task of regulatory proteins in all organisms. Thus, most research focused mainly on transcriptional and post-translational regulations. However, recent studies have implicated that microRNAs (miRNAs), a family of about 22-nucleotide small noncoding RNAs that regulate stability or translation of mRNA transcripts at the post-transcriptional level, may play crucial roles in modulating almost all cellular processes ranging from development and metabolism to apoptosis, signaling pathways, and diseases such as cancer (Ambros 2004; Bushati and Cohen 2007; Stefani and Slack 2008). As post-transcriptional gene suppressors, miRNAs regulate gene expression by base pairing to target mRNA molecules at conserved sites in the 3′ untranslated regions of the mRNAs, ultimately leading to a reduction in the levels of protein encoded by the target mRNAs (Filipowicz et al. 2008). Extensive evidence suggests that this suppression can occur by either translational repression or mRNA cleavage (Filipowicz et al. 2008; Bartel 2004; Valencia-Sanchez et al. 2006; Guo et al. 2010). In the former, miRNAs act as catalytic factors, preventing the initiation of translation, suppressing the production of proteins. In the latter, miRNAs act in a non-catalytic fashion, leading to the degradation of the target mRNA and the miRNA itself (Wang and Raghavachari 2011). Through either mechanism, miRNAs can keep gene products at extremely low copy numbers. The regulatory roles of miRNAs have been a subject of research for the last several years, both experimentally and theoretically (Shimoni et al. 2007; Wang and Raghavachari 2011; Levine et al. 2007; Levine and Hwa 2008; Mehta et al. 2008; Osella et al. 2011; Mitarai et al. 2009; Bumgarner et al. 2009; Iliopoulos et al. 2009). Although some of the miRNAs have been well studied, the mechanisms of various functions and biological significance of miRNAs are still not well understood (Bumgarner et al. 2009; Iliopoulos et al. 2009; Tsang et al. 2007; Shalgi et al. 2007; Re et al. 2009; Martinez et al. 2008; Martinez and Walhout 2009; Yu et al. 2008; Inui et al. 2010; Ivey and Srivastava 2010; Johnston et al. 2005; Kim 2007; Fazi 2005; Juan et al. 2009; Bracken 2008; Li and Carthew 2005; Visvanathan et al. 2007; Xu et al. 2009; Zhao et al. 2009; Pospisil 2011).

Recently several studies have shown that the transcriptional regulation by transcription factors (TFs) and post-transcriptional regulation by miRNAs are often highly coordinated (Shimoni et al. 2007; Tsang et al. 2007; Shalgi et al. 2007; Re et al. 2009; Martinez et al. 2008; Martinez and Walhout 2009; Yu et al. 2008; Inui et al. 2010; Ivey and Srivastava 2010). Of particular relevance is the accumulating evidence that the interplay of miRNAs and transcriptional regulators such as activators and repressors regulates key developmental events and cell fate decisions (Johnston et al. 2005; Kim 2007; Fazi 2005; Juan et al. 2009; Bracken 2008; Li and Carthew 2005; Visvanathan et al. 2007; Xu et al. 2009; Zhao et al. 2009; Pospisil 2011). These observations imply that the existence of considerable crosstalk between the transcriptional and post-transcriptional layers. Therefore, miRNA functions can be fully understood only by addressing TF and miRNA regulatory interactions together in “mixed” networks. Interestingly, recently computational and experimental studies have identified several recurrent network motifs contained in these mixed networks (Shimoni et al. 2007; Tsang et al. 2007; Shalgi et al. 2007; Re et al. 2009; Martinez et al. 2008; Martinez and Walhout 2009; Yu et al. 2008; Inui et al. 2010; Ivey and Srivastava 2010), such as miRNA-mediated single-input modules in which an miRNA regulates a group of target genes (Shimoni et al. 2007), and miRNA-mediated feedback and feed-forward loops (Tsang et al. 2007; Shalgi et al. 2007; Re et al. 2009; Martinez et al. 2008), as has been observed in transcriptional regulation networks of bacteria and yeast (Shen-Orr et al. 2002; Lee 2002). The simplest motif is a two-node miRNA-mediated double negative feedback loop (MDNFL) in which a TF suppresses an miRNA and the TF itself is negatively regulated by the miRNA.

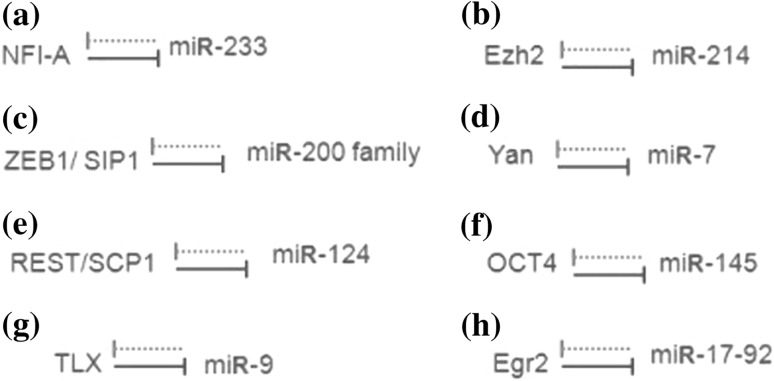
In this paper, we focus on this particular network motif, the MDNFL. The major motivation for this studying is that this specific motif has been reported in several recent experimental studies (Fazi 2005; Juan et al. 2009; Bracken 2008; Li and Carthew 2005; Visvanathan et al. 2007; Xu et al. 2009; Zhao et al. 2009; Pospisil 2011). For example, in human hematopoietic cells, NFI-A and miR-233 function in a double negative feedback loop to control granulocytic differentiation (Fazi 2005; Fig. 1a). In undifferentiated cells, miR-233 level is low and NFI-A level is high; however, upon retinoic acid signaling, miR-233 level increases due to the activation by the TF C/EBPa and NFI-A is then repressed, facilitating the differentiation to the myeloid lineage. This double negative feedback loop ensures mutually exclusive expression of miR-233 and NFI-A, thereby generating a bistable system, i.e., undifferentiated versus differentiated hematopoietic cells (Fazi 2005). Similarly, during skeletal muscle development, Ezh2 and miR-214 form a double negative feedback loop to regulate skeletal muscle cell differentiation (Juan et al. 2009; Fig. 1b). In undifferentiated myoblasts, Ezh2 is highly expressed and represses miR-214. Upon differentiation, MyoD/myogenin expression is activated and promotes transcription of miR-214, which in turn negatively regulates Ezh2 by inhibiting translation of its mRNA and thus reducing Ezh2 expression, ensuring complete differentiation of skeletal muscle cells (Juan et al. 2009). Moreover, in embryologic development, a double negative feedback loop between ZEB1-SIP1 and the miRNA-200 family controls epithelial-mesenchymal transition (Bracken 2008; Fig. 1c). In epithelial cells, a stable state is maintained by a high miR-200 level, which inhibits ZEB1/SIP1 and hence increases the expression of ZEB-repressed epithelial genes. The transition to a mesenchymal state can be induced by TGF-h, which increases the ZEB1-SIP1 level. A high ZEB1-SIP1 level in turn instigates and maintains a mesenchymal state through the repression of miR-200 by ZEB1-SIP1 (Bracken 2008). Likewise, in Drosophila eye development, the reciprocal repression between miR-7 and Yan ensures their mutually exclusive expression pattern: Yan is expressed in progenitor cells and miR-7 is expressed in photoreceptor cells (Li and Carthew 2005; Fig. 1d). The transition can be induced by the EGFR signaling, which transiently triggers Yan degradation. A decrease in Yan level relieves miR-7 from transcriptional repression, subsequently leading to the depletion of Yan in photoreceptor cells (Li and Carthew 2005). Moreover, during embryonic central nervous system development, a double negative feedback loop between the anti-neural REST/SCP1 and proneural miR-124 pathways contributes to a rapid and efficient transition of cellular phenotypes between neural progenitors and post-mitotic neurons (Visvanathan et al. 2007; Fig. 1e). In nonneuronal cells including neural progenitors, the REST/ SCP1 complex transcriptionally represses expression of miR-124 and other neuronal genes. As the REST level decreases during neurogenesis, miR-124 expression is derepressed, and subsequently, miR-124 post-transcriptionally suppresses multiple anti-neural factors including SCP1, resulting in further inhibition of the anti-neural pathway by REST/SCP1. This regulatory loop may represent key mechanisms to sense the intricate balance between proneural and anti-neural cues during development, to coordinate robust neuronal gene expression, and to confer neuronal identity in a timely manner (Visvanathan et al. 2007). In addition, upon initiation of embryonic stem cell differentiation, reciprocal inhibition of miR-145 and OCT4 contributes to irreversible silencing of self-renewal and pluripotency programs (Xu et al. 2009; Fig. 1f). Similar MDNFL motifs are also found in regulating the balance between neural stem cell proliferation and differentiation (Zhao et al. 2009; Fig. 1g), and PU.1-directed macrophage differentiation (Pospisil 2011; Fig. 1h). These experimental observations imply that this basic module may function as a bistable switch to regulate cell fate decisions such as differentiation during development. Actually, it has been shown that double negative feedback loops can act as bistable switches both experimentally and theoretically (Gardner et al. 2000; Ferrell 2002; Ferrell and Xiong 2001; Chatterjee et al. 2008). However, it is not clear whether the MDNFL can behave as a bistable switch. It is also not known the possible functions and biological significance of the miRNA in the MDNFL.

Fig. 1.

Biological examples of the MDNFL motif. a MDNFL controls granulocytic differentiation in human hematopoietic cells (Fazi 2005). b MDNFL regulates skeletal muscle cell differentiation during skeletal muscle development (Juan et al. 2009). c MDNFL regulates epithelial-mesenchymal transition during embryological development (Bracken 2008). d MDNFL promotes photoreceptor differentiation in the Drosophila eye (Li and Carthew 2005). e MDNFL contributes to a rapid and efficient transition of cellular phenotypes between neural progenitors and post-mitotic neurons during embryonic central nervous system development (Visvanathan et al. 2007). f MDNFL contributes to irreversible silencing of self-renewal and pluripotency programs upon initiation of embryonic stem cell differentiation (Xu et al. 2009). g MDNFL controls the balance between neural stem cell proliferation and differentiation (Zhao et al. 2009). h MDNFL regulates PU.1-directed macrophage differentiation (Pospisil 2011). The solid and dotted lines denote transcriptional and post-transcriptional regulations, respectively

To address these questions, we propose a general computational model for the MDNFL based on biochemical regulations and explore its dynamics by using bifurcation analysis. Our results show that the MDNFL can indeed behave as a bistable switch. This functional feature is in agreement with experimental observations of the widespread appearance of miRNAs in fate decisions during development. Importantly, it is found that under the interplay of a TF and an miRNA, the MDNFL model can behave as switches for wide ranges of parameters even without cooperative binding of the TF. It thus provides a novel mechanism to induce bistability through this combinatorial regulation even without cooperativity in the regulation. In addition, we also investigate how extrinsic noise affects dynamic behavior of the MDNFL. Interestingly, it is found that when the MDNFL is in the bistable region, the MDNFL system can switch from one steady state to the other and meanwhile the production of either miRNA or protein is amplified significantly by choosing the appropriate extrinsic noise source. From an engineering perspective, this noise-based switch and amplifier for gene expression is very easy to control because carefully tuning noise strength is not needed.

Deterministic model and bifurcation analysis for the MDNFL

Deterministic model for the MDNFL

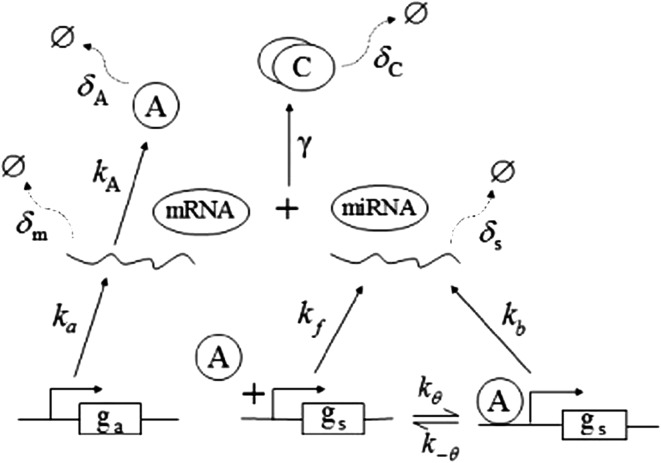
In this paper, we are mainly interested in analyzing the dynamics of the MDNFL and see what can be achieved in the simplest setting. Thus, different cellular compartments and separate concentrations for the nucleus and cytoplasm are not considered and biochemical regulations are modeled by simple rate equations. The proposed MDNFL model is depicted schematically in Fig. 2. It involves two genes g_a, g_s, their corresponding transcripts, mRNA, miRNA, and a protein A encoded by g_a. The protein A regulates transcription of gene g_s and the miRNA base pairs with the mRNA to forms the complex C.

Fig. 2.

The proposed model of the MDNFL motif. The Greek letters denote different parameters of the model and their meanings are explained in the text

Extensive evidences suggest that the mechanisms of microRNA-mediated gene regulation can be translational repression or destabilization of its target mRNAs (Valencia-Sanchez et al. 2006), i.e., miRNAs can either decrease the rate of translation or increase the degradation of its target mRNAs. Here, we choose to model the effect of miRNA regulation by taking the degradation rate of the target mRNA as a function of miRNA concentration. However, we note that the alternative choice of a translation rate of the target mRNAs as a function of miRNA concentration does not qualitatively alter the results below. The time evolution of the concentrations of the species in the MDNFL can be described by the following four deterministic rate equations:

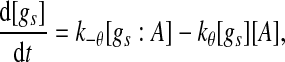1

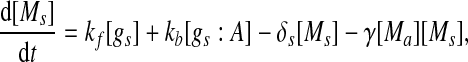2

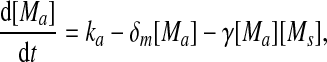3

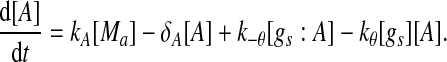4

In the above equations, [g_s], [g_s : A ], [M_s], [M_a], and [A], respectively, denote the concentration of free gene g_s, gene g_s with A bound to its promoter, miRNA, mRNA, and protein A. As in Francois and Hakim (2005), here the cellular volume is taken as volume unit and thus the concentrations and the number of the species are equivalent. It is assumed that there is only a single copy of gene g_s in the cell, i.e., [g_s] + [g_s : A] = 1 mol. Therefore, [g_s] can also represent the probability that gene g_s is free without A bound to its promoter. Particularly, A proteins bind to the promoter of gene g_s at a rate k_θ and when bound they dissociate at a rate k_−θ. The miRNA M_s is transcribed at a rate k_b when A binds to gene g_s or at a rate k_f otherwise. Thus, k_b > k_f corresponds to transcriptional activation by protein A and k_b < k_f to transcriptional repression, which will be focused on in this paper. Since regulation of gene g_a is not considered, it is simply assumed that mRNA M_a is produced at a given basal rate k_a. The mRNA M_a is translated into protein A at a rate k_A. δ_s, δ_m, and δ_A are the degradation rates for M_s, M_a, and A, respectively. γ is the base pairing rate of the miRNA with the mRNA. Here we assume that the base pairing is irreversible, consistent with the fact that the complex formed by miRNA and mRNA is extremely stable or rapidly degraded, and thus the complex needs not to be treated as a dynamical variable. Throughout this paper except if otherwise stated, we fix parameters as follows: 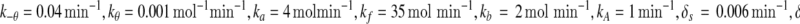and 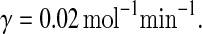In general, the range of each parameter value above is rather wide and here it is chosen to be typical in vivo value. It should be noted that all the above parameters were either directly taken from literature or estimated based upon analogous biological systems (Shimoni et al. 2007; Levine et al. 2007; Levine and Hwa 2008; Francois and Hakim 2005; Khanin and Vinciotti 2008; Aguda et al. 2008).

Steady states, bistable switches, and one-way switches

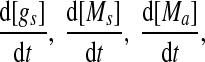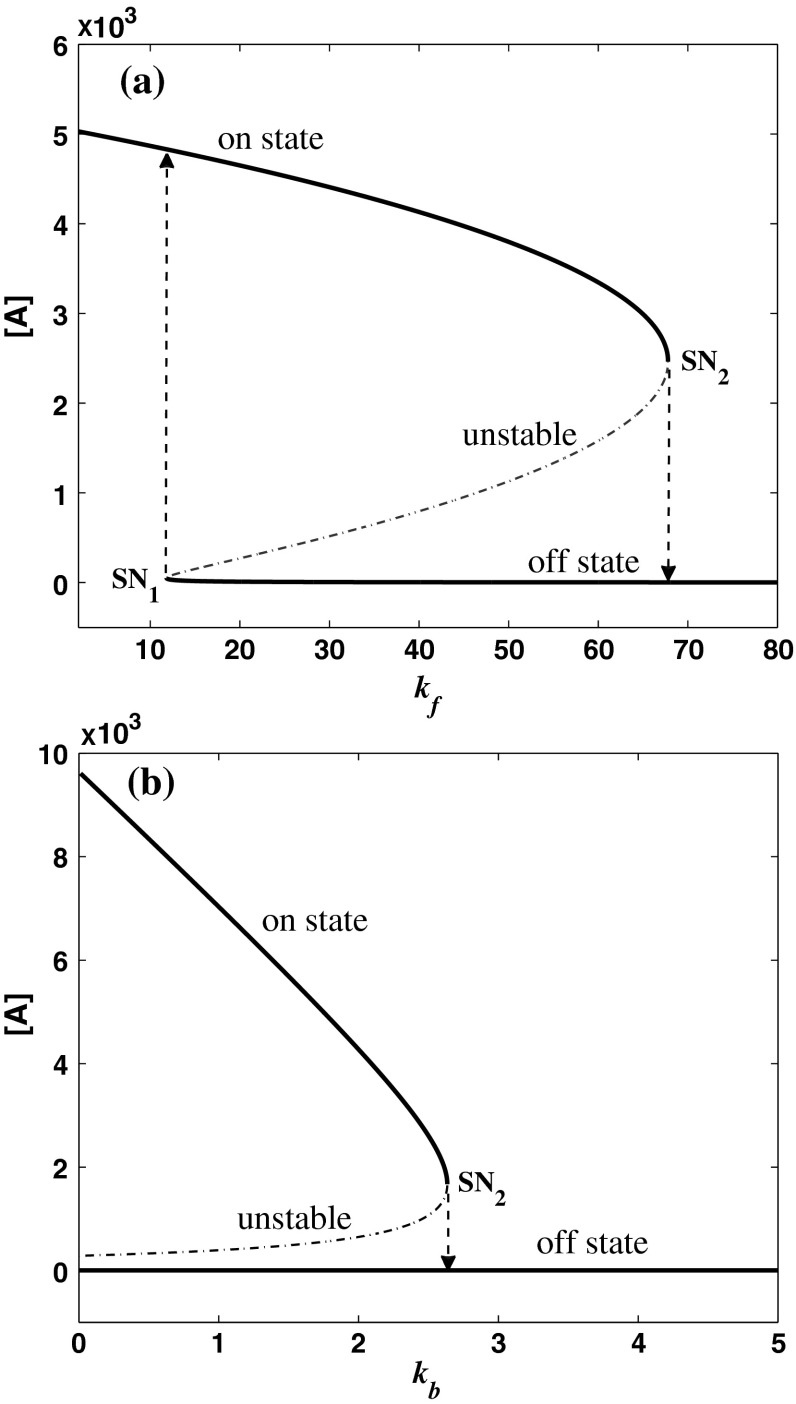
To probe the dynamics of the MDNFL, we first investigate how the steady-state value of [A] changes as a function of the different parameters in Eqs.(1)–(4) by performing bifurcation analysis. In the steady state, the rates of change of and 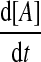are zero. A system behaves as a bistable switch if it has two stable equilibria in the appropriate parameter regime. Figure 3a shows the bifurcation diagram of system (1)–(4) as a function of the free g_s promoter transcription rate k_f. The two saddle-node bifurcation points 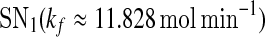and 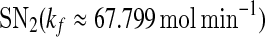enclose a bistable region. For any k_f within this region, the system has two stable equilibria and one unstable equilibrium, which are represented by solid and dash-dotted lines, respectively. The two stable equilibria in the bistable region correspond to low and high values of [A], respectively. For convenience, we denote the low/high protein concentration as the off/on state. It can be seen that a region of bistability separates two regions of monostability, bistability exhibits only for intermediate k_f values. The two stable state branches monotonically decrease with k_f because the miRNA concentration increases with k_f and thus the unpaired mRNA concentration decreases and further the production of the protein is reduced. At a specific value of k_f in the bistable region, the choice between the stable equilibria is history-dependent, i.e., the final state depends on initial conditions (Ferrell 2002). If the value of k_f is initially small, the system ends up in the on state. As k_f increases along the upper stable branch, A remains to be in the on state until the bifurcation point 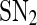is reached. When k_f is further increased, the on state vanishes, and the system moves towards the lower stable branch, corresponding to the off state. Then, if we decrease k_f, the system proceeds along the lower stable branch until 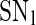is reached and another transition occurs, which brings the system back to the upper stable branch, an on state. The system therefore exhibits some hysteresis. Hysteresis is a property of bistable systems and of the potential importance in biological switching. First, it reduces the probability that a switch will repeatedly flip back and forth between two states when the bifurcation parameter is hovering near its threshold value, thereby providing an unambiguous threshold switching mechanism and buffering against the noise (Ferrell and Xiong 2001). Second, it provides a potential mechanism for biochemical memory (Zhang et al. 2007). During the maturation of Xenopus oocyte, for example, the p42 MAPK/Cdc2 system can keep a long-term memory of a transient differentiation stimulus (Xiong and Ferrell 2003). There are now several known systems in which bistability and hysteresis have been observed experimentally (Gardner et al. 2000; Xiong and Ferrell 2003; Acar et al. 2005; Ozbudak et al. 2004; Sha et al. 2003; Pomerening et al. 2003).

Fig. 3.

Bifurcation diagrams of the MDNFL model. a The bifurcation diagram as a function of k_f. b The bifurcation diagram as a function of k_b. Solid and dash-dotted lines denote stable and unstable equilibria, respectively. SN₁ and and SN₂ represent the saddle-node bifurcation points

Biologically speaking, the above results indicate that when the free transcription rate of the miRNA lies outside the region enclosed by the two saddle-node bifurcation points, a smaller/larger free transcription rate will lead to a higher/lower protein concentration. When the free transcription rate lies in the region, however, a smaller/larger free transcription rate may lead to a lower/higher protein concentration, depending on the initial conditions. As the free transcription rate of the miRNA increases gradually from a small value, the protein concentration will decrease gradually but remain in high level until 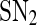is reached, where it switches to a low level. After that, the protein concentration will stay in the low level unless the free transcription rate is reduced and exceeds 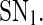This is consistent with the experimental observations that in human hematopoietic cells, the increase of miR-233 level due to the activation by the TF C/EBPa upon retinoic acid signaling, similar to the increase of the free transcription rate, can facilitate undifferentiated hematopoietic cells where miR-233 level is low and NFI-A level is high differentiate to the myeloid lineage (Fazi 2005; Fig. 2a), and the experimental observations that during skeletal muscle development, the increase of miR-214 level promoted by MyoD/myogenin which is activated upon differentiation, ensure undifferentiated myoblasts where Ezh2 is highly expressed complete differentiation (Juan et al. 2009; Fig. 2b). Similarly, as the free transcription rate decreases gradually from a large value, the protein concentration will increase gradually but stay at low level until 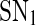is reached, where it switches to a high level. After that, the protein concentration will remain in the high level if the free transcription rate is not increased.

The bifurcation diagram of system (1)–(4) with k_b as a control parameter is shown in Fig. 3b. It indicates that as k_b increases along the upper stable branch, A continues to be in the on state until some critical value, 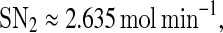is exceeded, at which a discontinuous jump to the off state occurs and the system become monostable. Then, if k_b decreases, A stays at the off state indefinitely, i.e., the transition is irreversible. Such kind of switches is termed irreversible or one-way switches (Tyson et al. 2003). The one-way switch is an extreme manifestation of hysteresis, i.e., its lower stable solution branches into the negative domain but is actually eliminated due to a physically meaningful restriction. Based on such hysteresis and irreversibility, bistable switches can make a reliable decision in many physiological processes, as in the yeast galactose-utilization network (Acar et al. 2005; Ramsey 2006), the MAPK/PKC signaling network (Bhalla and Iyengar 2001; Bhalla et al. 2002), and the p42 MAPK cascade in Xenopus oocytes (Ferrell and Machleder 1998).

The effect of parameter variations on the bistable regime

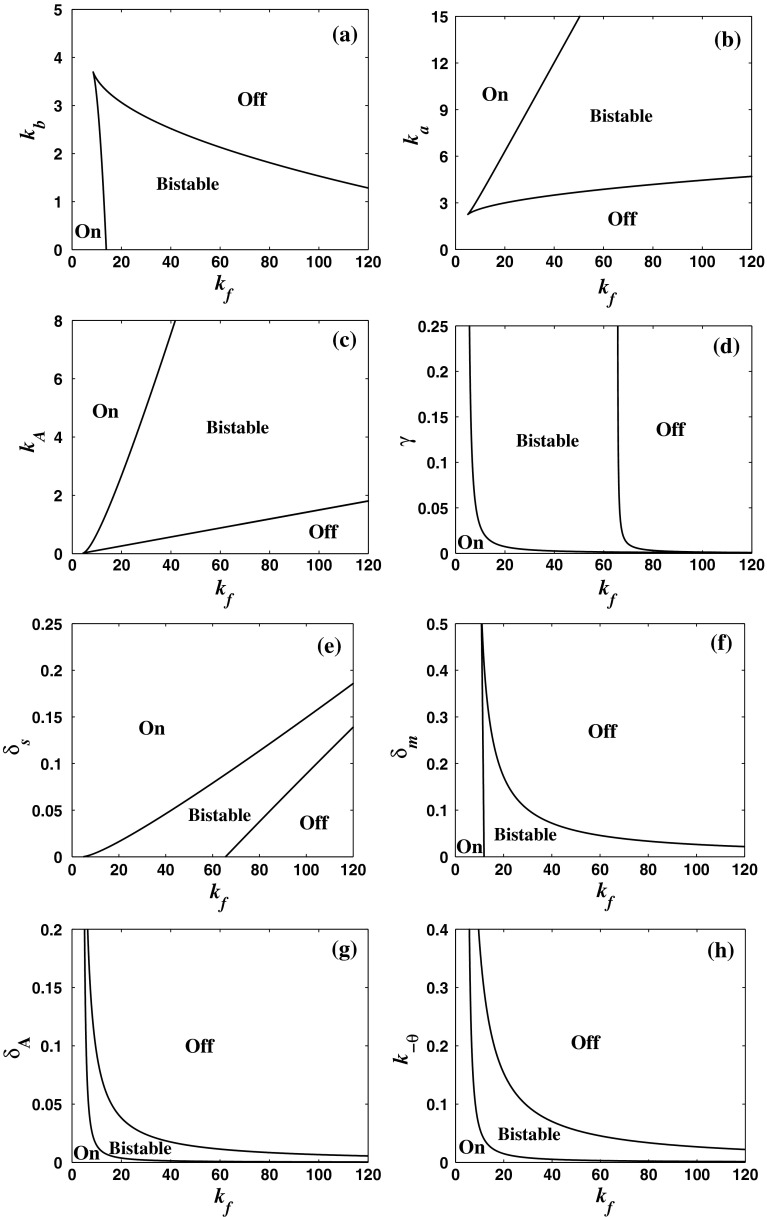
In order to see whether the MDNFL model can behave as switches for wide ranges of parameters, the codimension two bifurcation diagram of system (1)–(4) is constructed for all the important parameters to determine the range of bistable regime. Figure 4a shows the bifurcation diagram of system (1)–(4) with k_f and k_b as the bifurcation parameters. It can be seen that the region of bistability becomes wider and the upper threshold of k_f increases as k_b decreases due to the fact that a larger k_f is needed to compensate inefficiency of the miRNA level at a smaller k_b so as to produce bistability. Figure 4b illustrates the bifurcation diagram of system (1)–(4) with k_f and k_a as the bifurcation parameters. It is shown that with increasing k_a, the region of bistability becomes wider and the lower and upper thresholds increase moderately because a larger k_f is required to compromise efficiency of the mRNA level at a larger k_a in order to induce bistability. For a fixed k_f, when we increase the basal transcription rate k_a, the system undergoes a transition from a monomodal off state to a bistable region and then to a monomodal on state. This is consistent with the experimental observations that increasing the ZEB1-SIP1 level activated by TGF-h, similar to increasing k_a, can induce a transition from a epithelial state maintained by a high miR-200 level and a low ZEB1-SIP1 level to a mesenchymal state where the ZEB1-SIP1 level is high and the miR-200 level is low (Inui et al. 2010; Bracken 2008; Fig. 2c). The bifurcation diagram of system (1)–(4) with k_f and k_A as the bifurcation parameters is shown in Fig. 4c. It can also be seen that with increasing k_A, bistable regime becomes wider and the lower and upper thresholds increase moderately. In addition, decreasing the production rate k_A from a large value for a fixed k_f will shift the system from a monomodal on state, across a bistable region, to a monomodal off state. Figure 4d shows the bifurcation diagram of system (1)–(4) with k_f and γ as the bifurcation parameters. It indicates that when there is no the negative post-transcriptional regulation, i.e., at γ = 0, the system is monostable. However, moderately increasing γ from zero can shift the system into bistable regime. Therefore, the negative regulation mediated by the miRNAs can induce bistability. In addition, the region of bistability becomes wider with increasing γ. A larger miRNA-mRNA base pairing strength γ drives the system to the off sate and so enlarges the bistable parameter range. Figure 4e shows the bifurcation diagram of system (1)–(4) with k_f and δ_s as the bifurcation parameters. With increasing k_f, bistability emerges, depending on the values of δ_s. In addition, the bistable regime becomes narrow while the lower and upper thresholds increase moderately with increasing δ_s. For a fixed δ_s, when we increase k_f, the system undergoes a transition from a monomodal on state to a bistable regime and then to a monomodal off state. The bifurcation diagram of system (1)–(4) with k_f and δ_m as the bifurcation parameters is shown in Fig. 4f. Since decreasing the degradation rate of the mRNA δ_m has similar effect with increasing the basal transcription rate of the mRNA k_a, the region of bistability becomes wider and the upper threshold of k_f increases as δ_m decreases. While the value of δ_m is fixed, increasing the value of k_f from zero will shift the system from a monomodal on state, across a bistable region, to a monomodal off state. The bifurcation diagram of system (1)–(4) with k_f and δ_A as the bifurcation parameters is shown in Fig. 4g. By increasing the degradation rate of the protein δ_A from a small value, the transition begins with a monomodal on state to a a bistable region then to a monomodal off state. This is consistent with the experimental observations that the degradation of protein Yan transiently triggered by the EGFR signalling, similar to the increase of δ_A, can induce a transition from a progenitor cell state where Yan is expressed to a photoreceptor cell sate where miR-7 is expressed (Li and Carthew 2005; Fig. 2d). The parameter k_−θ exhibits a similar influence as the parameter δ_A. When we increase k_−θ, the system undergoes a transition from a monomodal on state to a a bistable region then to a monomodal off state, as seen in Fig. 4h.

Fig. 4.

Codimension two bifurcation diagrams of the MDNFL model. ak_f and k_b as the bifurcation parameters. bk_f and k_a as the bifurcation parameters. ck_f and k_A as the bifurcation parameters. dk_f and γ as the bifurcation parameters. ek_f and δ_s as the bifurcation parameters. fk_f and δ_m as the bifurcation parameters. gk_f and δ_A as the bifurcation parameters. hk_f and k_−θ as the bifurcation parameters. The regions enclosed by the solid lines are bistable regions, outside of which the model is monostable

In summary, the above codimension two bifurcation diagrams indicate that in the MDNFL model each parameter can be varied individually for a wide range, while preserving bistability. This means that the MDNFL model can behave as switches for wide ranges of parameters. Moreover, it should be pointed out that here we assume that the production of miRNA, M_s, is regulated by protein A, through binding of a single protein A to its promoter, g_s, that is, without cooperative binding of the TF to its promoter. In this case, the system is always monostable if the miRNA-mediated regulation does not exist (Ferrell and Xiong 2001; Lipshtat et al. 2006) [ also see Fig. 4d]. On the other hand, the miRNA-mediated regulation, if works solely, also leads to monostability (Levine et al. 2007). Interestingly, under the interplay of the TF and miRNA, it is found that the MDNFL model can behave as switches for wide ranges of parameters even without cooperative binding of the TF. It thus provides a novel mechanism to induce bistability through this combinatorial regulation even without cooperativity in the regulation, which is fundamentally distinct from the generation of bistability by intrinsically nonlinear positive feedback regulation, such as protein dimerization and cooperative formation of heterodimers (Ferrell 2002; Ferrell and Xiong 2001; Zhdanov 2009; Liu et al. 2011). The evidence for use of the MDNFL motif as switches has been reported recently, especially on cell fate decisions (Fazi 2005; Juan et al. 2009; Bracken 2008; Li and Carthew 2005; Visvanathan et al. 2007; Xu et al. 2009; Zhao et al. 2009; Pospisil 2011). It is hoped this novel mechanism can be realized in artificial genetic networks in the future.

Stochastic model and noise-induced dynamics for the MDNFL

The deterministic analysis above successfully demonstrates how the steady-state values of the MDNFL system shift as parameter values change. However, cellular processes at the molecular level are inherently stochastic (Balàsi et al. 2011). Numerous studies have revealed the importance of stochastic or probabilistic effects in biological systems where the number of molecules is low enough for noise to be important, and the deterministic chemical kinetic descriptions are limited (Lipshtat et al. 2006; Hasty et al. 2000; Vilar et al. 2002; Rao et al. 2002; Wang et al. 2007; Li and Li 2008). In addition, noise can also have significant effects on the stability and synchronization of genetic regulatory networks as well as neuronal networks (Shi et al. 2008; Wang et al. 2009; Guo 2011; Wu et al. 2012). There are two sources of noise in biological systems: intrinsic noise and extrinsic noise. Intrinsic noise originates from discrete nature of biochemical events such as transcription, translation, multimerization, and protein/mRNA decay processes (Raj and van Oudenaarden 2008). On the other hand, extrinsic noise results from perturbations in the extrinsic environment or the random variations in one or more of the externally set control parameters, such as the rate constant of the transcription of a specific gene (Hasty et al. 2000). In addition, extrinsic and intrinsic noise often exist in biological system simultaneously. In this section, we mainly focus on how extrinsic noise affects the dynamic behavior of the MDNFL. The effect of intrinsic noise on the dynamic behavior of the MDNFL will be analyzed systematically elsewhere.

Stochastic model for the MDNFL

As shown in Fig. 2, the two transcription rate of gene g_s, k_b and k_f, influence the dynamics of the MDNFL. Although the transcription is described as a single biochemical reaction in our model, it actually consists of a complex sequence of reactions (Hasty et al. 2000). It is natural to assume that this part of the gene regulatory sequence is likely to be affected by fluctuations of many internal or external parameters, and it is interesting to study the effect of such noise on the dynamics of the MDNFL. In order to introduce such extrinsic noise into system (1)–(4), we adapt an approach in the spirit of Ref. (Hasty et al. 2000). We vary the transcription rates by allowing the parameters k_b and k_f in system (1)–(4) to vary stochastically, that is, 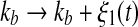and 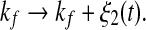In such a manner, we obtain the following stochastic model:

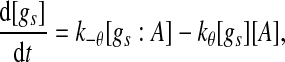5

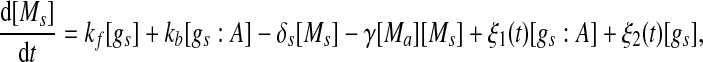6

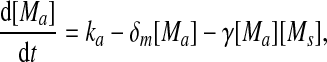7

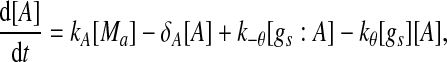8

where ξ₁(t) and ξ₂(t) are random terms with zero means 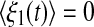and 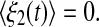In order to encapsulate rapid random fluctuations, we make the standard requirement that the autocorrelation be “δ-correlated”, i.e., the statistics of ξ_i(t) are such that 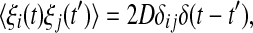where δ_ij is the Kronecker delta, δ(t − t′) is the Dirac function and D is the constant that characterizes the strength of the perturbation. The above stochastic model is numerically simulated using the Euler–Maruyama scheme with the integration time step 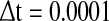(Higham 2001).

Noise-induced switching and amplifying

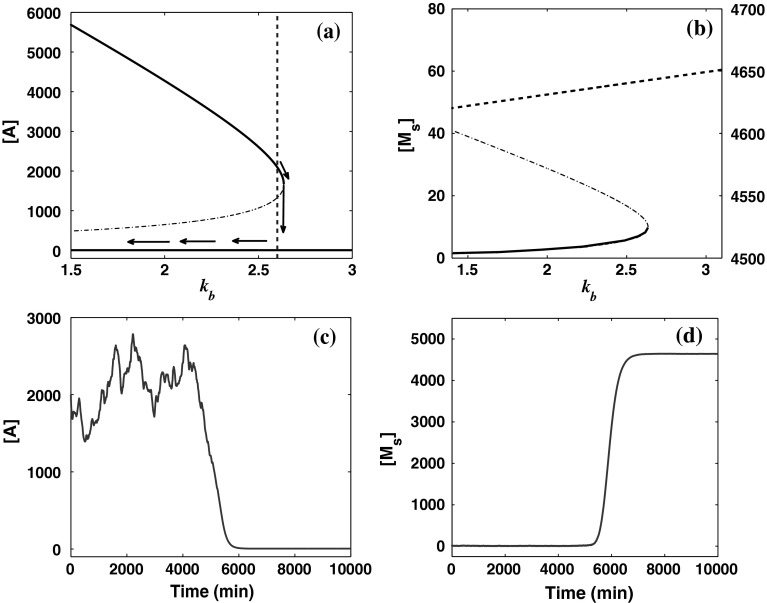
To obtain the qualitative effect of the external noises on the dynamics of system (1)–(4), we first use the bifurcation diagram to anticipate the effect of fluctuations allowed in the transcription rates. For the deterministic system, the steady-state values of the concentration of protein A and miRNA M_s for different values of parameter k_b are shown in Fig. 5a and b. It can be seen that the system undergoes a saddle-node bifurcation at 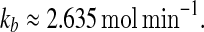For the values of k_b larger than the saddle-node bifurcation point, the system has one unique stable equilibrium with low A and high M_s concentrations, whereas for other values of k_b, the system has three equilibria: one is unstable and the other two stable, where one stable equilibrium corresponds to low A and high M_s concentrations, and the other corresponds to high A and low M_s concentrations. In the absence of noise, the concentrations of protein A and miRNA M_s will converge to one of the two stable equilibria completely determined by the initial state of the system. A comparison of Fig. 5a and b shows that the upper stable branch in Fig. 5a is steep, while the lower stable branch in Fig. 5b is flat. Therefore, we can anticipate that when the system is in the bistable region and has high A and low M_s concentrations, if the parameter k_b varies, the variations in the concentration of protein A will be notably large, while the fluctuations in the concentrations of miRNA M_s will be small. If the system lies in the other stable equilibrium with low A and high M_s concentrations, however, only a mild change in both the concentrations of A and M_s takes place due to the flat lower stable branch in Fig. 5a and the flat upper stable branch in Fig. 5b.

Fig. 5.

Results for external noise affecting k_b with parameter values 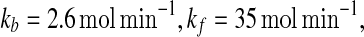and D = 0.75. a Bifurcation diagram for the concentration of protein A as a function of k_b. The dotted vertical line is the parameter for which stochastic simulation was carried out. b Bifurcation diagram for the concentration of miRNA M_s as a function of k_b. The steady state with a high M_s concentration is plotted in the dashed line and corresponds to the right Y axis. The other two states are in the solid line and dash-dotted line, respectively, and corresponds to the left Y axis. c The time evolution of the concentration of protein A. d The time evolution of the concentration of miRNA M_s. Stable and unstable states are represented by solid (or dashed) and dash-dotted lines, respectively

In order to verify the above observation quantitatively, we next incorporate extrinsic noise to make k_b stochastically vary and investigate the temporal behavior of the system under the fluctuations. We simulated the stochastic model for the MDNFL [Eqs. (5)–(8)] with a large noise intensity, D = 0.75. Initially, we fix the parameter value 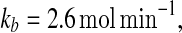as indicated by a broken vertical line in Fig. 5a, such that the system is in the bistable region. The simulation results beginning with the concentration of protein A equal to its upper value of approximately 2,000 and miRNA M_s concentration about 0 are presented in Fig. 5c and d. At first, the fluctuations in the concentration of protein A are quite large while the concentration of miRNA M_s is nearly unchanged as we expected. Then, at around 5,500 min, the concentration of A quickly drops to the lower value. Meanwhile, the concentration of M_s quickly jumps to its upper value and remains in there with quite small variations, as anticipated. This phenomenon indicates that the extrinsic noise introduced into the transcription rate is sufficient to induce the system to switch from one stable state to the other by crossing the unstable state. When the number of miRNA M_s is randomly fluctuated to a comparable value with that of mRNA M_a, most of the mRNA molecules are expected to base pair rapidly with the miRNA molecules and degraded, which will result in a low expression of protein A and thus leave the gene g_s unregulated. In this case, the concentration of miRNA M_s will soon build up to a rather high values if k_f is large enough, i.e., the transition occurs.

On the other hand, a large fluctuation in the concentration of protein A before the switching implies that the amount of the protein is quite sensitive to the variation in the parameter k_b if much more protein A exists in the system than miRNA M_s. But after the fast transition occurs at around 5,500 min, flat curves in both Fig. 5c and d means that the other steady state is nearly unaffected by the fluctuations in the value of k_b and thus is impossible to switch back unless noise intensity increases. This suggests that dynamic behavior of the MDNFL can be either sensitive or robust to the same perturbation affecting k_b depending on the specific state at which the MDNFL initially stays (Stelling et al. 2004), and under such perturbation with large enough strength, the MDNFL is very likely to switch to or remain in the robust state with low A and high M_s concentrations. It is also noticed that in the fast transition, the concentration of miRNA M_s increases abruptly by over three orders of magnitude in a very short time if k_f is large enough. This character suggests that the extrinsic noise affecting k_b might be used to amplify miRNA M_s’s production.

Similar results can be obtained for the extrinsic noise affecting k_f when the value of the parameter k_f is initially set to 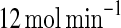except that the state with high A and low M_s concentrations that is sensitive to the fluctuations in k_b discussed above is robust to the random variation of k_f, and the other state with low A and high M_s concentrations which is robust to the fluctuations in k_b is sensitive to the random variation of k_f, as suggested in Fig. 2a. As a result, if the MDNFL is affected by the perturbation affecting k_f, contrary to the above result, the MDNFL is very likely to switch to or remain in the state with high A and low M_s concentrations. Likewise, the concentration of protein A may increase significantly during the switching process. This interesting feature of the MDNFL allows us to obtain the desired state switch and amplifying in the MDNFL easily by choosing the appropriate extrinsic noise source. From an engineering perspective, this character makes this type of switch easy to control because accurately tuning the strength and timing of noise has been done in Hasty et al. (2000) is not needed here.

Discussion and conclusion

The importance of post-transcriptional regulation by miRNAs has recently been recognized in diverse biological processes in animals and plants (Ambros 2004; Bushati and Cohen 2007; Stefani and Slack 2008; Inui et al. 2010; Ivey and Srivastava 2010). Moreover their profiles are altered in several human diseases (Alvarez-Garcia and Miska 2005; Esquela-Kerscher and Slack 2006), making miRNAs a major focus of research in nowadays molecular biology. Recently, possible functions and biological significance of miRNAs have been the subject of both experimental and theoretical studies (Shimoni et al. 2007; Wang and Raghavachari 2011; Levine et al. 2007; Levine and Hwa 2008; Mehta et al. 2008; Osella et al. 2011; Mitarai et al. 2009; Bumgarner et al. 2009; Iliopoulos et al. 2009). Some special functional features of miRNAs have been indicated by mathematical modeling and dynamical simulations, e.g., a tunable threshold-linear expression pattern and repression of fluctuation in the silence regime (Levine et al. 2007; Levine and Hwa 2008), better than TF-based regulation at filtering input noise but suffers higher intrinsic noise arising from transcriptional bursting (Mehta et al. 2008), and fine-tuning of a target protein level and an efficient noise control (Osella et al. 2011). However, most of the previous works focus only on how miRNAs post-transcriptionally regulate the target protein levels, work solely, and induce monostability. Recently, several double negative feedback loops involving miRNAs and TFs have been found experimentally in a variety of organisms (Martinez et al. 2008; Johnston et al. 2005; Kim 2007; Fazi 2005; Juan et al. 2009; Bracken 2008; Li and Carthew 2005; Visvanathan et al. 2007; Xu et al. 2009; Zhao et al. 2009; Pospisil 2011). It has been shown that such composite double negative feedback loop (MDNFL) occurs frequently, and hence constitutes a network motif (Tsang et al. 2007; Martinez and Walhout 2009). To our knowledge, the issue about possible functions of this basic motif and the effects of combinational regulation by TFs and miRNAs have not yet been well addressed. To better understand the dynamical properties of this basic motif, we have presented a general computational model for the MDNFL and explored its dynamics by using bifurcation analysis. Our results show that there exist wide ranges of parameters where the MDNFL can behave as switches. These functional features are consistent with the widespread appearance of miRNAs in fate decisions such as differentiation during development. In addition, positive feedback and cooperativity in the regulation of gene expression are generally considered to be necessary for obtaining bistable expression states (Ferrell and Xiong 2001; Lipshtat et al. 2006). Interestingly, here it is found that under the combinatorial regulation by a TF and an miRNA, the MDNFL model can behave as switches for wide ranges of parameters even without cooperative binding of the TF. It thus provides a novel mechanism to induce bistability through this combinatorial regulation even without cooperativity in the regulation. We hope this mechanism can be realized in artificial genetic networks in the future.

On the other hand, cellular processes at the molecular level are inherently stochastic (Balàsi et al. 2011). The origin of stochasticity can be attributed to internal and external noises. It is well known that noise can have great impacts on biological systems’ dynamical properties (Lipshtat et al. 2006; Hasty et al. 2000; Vilar et al. 2002; Rao et al. 2002; Wang et al. 2007; Li and Li 2008), for example, noise can induce sustained stochastic oscillation even though the corresponding deterministic system only yields steady state (Li and Li 2008). In this paper, we have also studied the effect of extrinsic noise on the dynamic behavior of the MDNFL. It is found that if the noise is considered, the MDNFL system can generate some different phenomena not observed in the corresponding deterministic model. More specifically, when the MDNFL system is in the bistable region, extrinsic noise fluctuating the two transcription rates of the miRNAs gene can induce the system quickly switch from one steady state to the other. In addition, any one of the two steady states is robust to one type of the two different extrinsic noises but sensitive to the other. This feature makes this type of switch easy to control because the requirement of carefully tuning noise strength is not considered. Moreover, during the transition process, the concentration of the miRNA (or the protein) is quite low before the switch can be amplified significantly.

The control of cellular functions through the design and manipulation of gene regulatory networks is an intriguing perspective in applications (Wang et al. 2007). Current gene therapy techniques are limited in that transfected genes are typically either in an “on” or “off” state (Hasty et al. 2000). For the effective treatment of many diseases, however, the expression of a transfected gene needs to be regulated in a systematic fashion. Thus, the development of extrinsically controllable noise-based switches and amplifiers for gene expression could have significant clinical implications and the results in this paper suggest that the MDNFL might be quite useful for that. To make this feature of MDNFL clinically applicable, it is important to look for an appropriate noise source. Sets of chemical reactions that affect the transcription of gene g_s might be used as the noise input of this switch. Moreover, it has recently been shown that manipulation of miRNAs is readily achievable in vivo and thus holds exciting promise for potential therapeutic applications for diseases associated miRNAs (krützfelt 2005; Elmèn 2008).

It has been widely recognized that a complicated living organism cannot be fully understood by merely analyzing individual components, and that interactions of those components or biomolecular networks in terms of structures and dynamics are ultimately responsible for an organism’s form, rhythms, and functions (Wang et al. 2008). But the intrinsic complexity of biomolecular networks inhibits us to understand them as a whole. Instead, researchers turn to study the building block, or motif, of these networks. Elucidating these motifs’ dynamics and functions would shed light on the whole networks’ behaviors. Computational models based on experimental data have been proven to be quite useful to solve these problems (Alon 2007). In this paper, we have proposed a simple computational model for the miRNA-mediated double negative feedback loop (MDNFL) motif and studied its functional characteristic motivated by this motif appears in regulation fate decisions in a variety of organisms (Martinez et al. 2008; Johnston et al. 2005; Kim 2007; Fazi 2005; Juan et al. 2009; Bracken 2008; Li and Carthew 2005; Visvanathan et al. 2007; Xu et al. 2009; Zhao et al. 2009; Pospisil 2011). Besides the minimal architecture discussed here, miRNA-mediated network motifs with other architectures can be similarly analyzed, such as miRNA-mediated feed-forward loops (Tsang et al. 2007; Shalgi et al. 2007; Re et al. 2009). It is expected that the insight gained from the study of these simple motifs could provide a basis for investigation of more complex networks assembled by simple building blocks. A more clear understanding of the miRNA-mediated motifs is also important for bio-engineering or artificial control of specified components, interactions, and even network functions. It is hoped that the results presented here could provide a new view on how gene expression is regulated and further guidance for experiments.

Finally, it is worth mentioning that a plausible method whereby a system may be experimentally probed for bistability has been proposed in (Hasty et al. 2000). The main idea is that in a bistable system, the threshold value of the control parameter required for the system to be switched from off to on state is different from that for transitioning in the reverse direction [also see Fig. 2]. Since the degradation parameter δ_A is easier to manipulate externally (Hasty et al. 2000), according to the suggestion given in (Hasty et al. 2000), one can perform an experiment for the MDNFL system by slowly increasing the degradation rate δ_A from a low initial value to see whether the concentration of protein A can abruptly jump to a lower value at some moment after a slow decrease. If so, one then reverses the direction of the experiment to observe whether the concentration of protein A can suddenly switch to a higher value at some point after a slow increase. If it occurs and the downward threshold value differs from that of the upward, then one can conclude that the MDNFL system is a bistable system. Similar methods have been used to probe for bistability in previous experimental studies (Gardner et al. 2000; Xiong and Ferrell 2003; Ozbudak et al. 2004). In addition, it should be pointed out that simple genetic network motifs are always embedded in a larger and more complex network, under some circumstances, it thus might be not easy for us to observe in vivo the phenomena predicted here due to the fact that the MDNFL no longer functions independently, but as pointed out in (Alon 2007) in many cases the functions can be preserved.