A unified model of autopolyploid establishment and evolution

Abstract

The prevalence of polyploidy among flowering plants is surprising given the hurdles impeding the establishment and persistence of novel polyploid lineages. New polyploid lineages are doomed to extinction through minority cytotype exclusion except in cases of strong assortative mating, reproductive assurance through selfing or vegetative reproduction, or large intrinsic fitness advantages. Thus, much work has focused on a search for adaptive advantages associated with polyploidy, such as increased competitive ability, enhanced ecological tolerances, or increased resistance to pathogens. Yet, no consistent adaptive advantages of polyploidy have been identified. Here we develop a model of a diploid population which sporadically gives rise to novel polyploids to investigate the potential for polyploid establishment and persistence in the absence of any intrinsic fitness advantages, and with only very small levels of initial assortative mating or niche differentiation generated by dosage effects of genome duplication. Our results show that by allowing assortative mating and competitive interactions to evolve, establishment of novel polyploid lineages becomes common. Additional scenarios where adaptive optima change over time reveal that rapid environmental change promotes the fixation of polyploid lineages. These results help to explain recent empirical findings that suggest many contemporary polyploid lineages arose during the Cretaceous-Tertiary extinction without invoking adaptive advantages of polyploidy.

Introduction

Polyploidy is ubiquitous among plants, with most flowering plants thought to be of polyploid origin and up to 31% of speciation events in ferns attributable to polyploidy (Masterson 1994; Otto and Whitton 2000; Soltis et al. 2007; Soltis 2005; Wood et al. 2009). In addition, molecular evidence demonstrates that polyploids frequently arise multiple times within single species (Ness et al. 1989; Segraves et al. 1999; Soltis and Soltis 2000). Together, these observations suggest that neopolyploids must be formed and become established at an appreciable rate.

The relatively frequent establishment of polyploid populations is surprising in light of the considerable forces opposing the establishment of neopolyploids. For instance, the minority cytotype in a randomly mating population will experience strong negative frequency dependent selection due to a large proportion of ineffective matings with the majority cytotype. Simply put, a neopolyploid has no one to mate with. This phenomenon, known as minority cytotype exclusion (MCE)(Levin 1975), is arguably the single largest hurdle to polyploid establishment. When accompanied by an initial decrease in fertility (Ramsey and Schemske 2002), and competition with well-adapted diploid progenitors (Otto 2007), establishment of neopolyploids would seem to be extremely unlikely.

Models developed to understand how polyploids could overcome MCE have identified several important possibilities. For instance, selfing or vegetative reproduction can offset the effects of being the minority cytotype (Kao 2007), and indeed species that reproduce by selfing have higher rates of polyploidy (Barringer 2007; Otto and Whitton 2000). However, most polyploids do not exclusively self or reproduce asexually; indeed the majority of autopolyploids may rely primarily on a mixed mating system (Husband e t al. 2008). Another possibility is assortative mating (Husband and Sabara 2004; Rodriguez 1996). If neopolyploids mate primarily amongst themselves, MCE is reduced or eliminated (Husband and Sabara 2004). However, studies of synthetic neopolyploids suggest that initial phenotypic divergence may not be sufficient to eliminate inter-cytotype pollen transfer (Husband et al. 2008). Finally, it has been suggested that polyploids may simply have a fitness advantage over their diploid progenitors, perhaps because a duplicated genome offers opportunities for novel adaptation (Chen 2007; Osborn et al. 2003). For instance polyploids may exhibit increased tolerance to drought and extreme temperatures (Levin 1983; Otto and Whitton 2000), increased resistance to pathogens (Oswald and Nuismer 2007), increased competitive ability (Levin 1983), and in the case of allopolyploids, hybrid vigor (Otto and Whitton 2000). However, even if polyploids do have these advantages, models still predict the polyploid lineage will be suppressed through minority cytotype disadvantage (Felber 1991), and perhaps more importantly, no general trend toward adaptive superiority has been demonstrated in extant polyploids (Burton and Husband 2000; Munzbergova 2007).

Another approach to understanding why polyploids are evolutionarily ubiquitous was put forward by Meyers and Levin (2006). Specifically, Meyers and Levin argued that even if polyploidy does not result in significant increases in adaptability, because it is irreversible, a polyploid ratchet ensues that accounts for the high frequency of polyploidy. Therefore, the polyploid ratchet can be thought of as a null model for the evolution of polyploidy. However, the polyploid ratchet hypothesis simply assumes that establishment occurs at a small rate and thus avoids the issue of establishment altogether.

Thus, we currently have a collection of models that identify specific scenarios favoring the establishment of individual polyploid populations, but lack broad empirical support, and a neutral model that explains the overall ubiquity of polyploidy but fails to explain how novel polyploid populations ever succeed in becoming established in the first place. In addition to these weaknesses, no existing models identify conditions favoring coexistence vs. replacement. In other words, why do polyploid lineages coexist with their diploid progenitors in some well studied systems (Segraves et al. 1999; Burton & Husband 1999; Halverson et al. 2008; Husband & Schemske 1998; Kao 2008; Felber-Girard et al. 1996; Hardy et al. 2000), yet replace their diploid progenitors in others, as appears to have been the case around the time of the Cretaceous-Tertiary extinction (Fawcett et al. 2009)?

We hypothesize that the establishment and subsequent evolutionary trajectory of polyploid lineages can largely be explained by the rapid evolutionary divergence of newly formed polyploid lineages. Because evolutionary divergence for key traits, such as flowering time, is likely to reduce the frequency of intercytotype matings and reduce the intensity of intercytotype competition, it provides the potential for novel polyploid populations to become established in the absence of any unique features of polyploidy per se. In order to investigate the possibility that evolutionary divergence for key reproductive traits such as flowering phenology or floral morphology is sufficient to explain the establishment, coexistence, and occasional dominance of polyploid populations, we developed and analyzed a genetically explicit model of a diploid population, which sporadically produces neopolyploid individuals. We used this model to answer three key questions: 1) under what conditions will polyploids arise and become established within the diploid population? 2) what conditions promote coexistence between cytotypes? and 3) when will a new polyploid lineage replace its diploid progenitor?

The Model

We modeled a population of an annual monoecious plant living in a habitat with a carrying capacity of K individuals. We assumed that individuals were characterized by their ploidy (2×, 3×, 4×) and a single phenotype, p, which was determined by multiple loci, each of which could have several possible alleles. This single phenotype, p, was assumed to 1) be subject to stabilizing selection, 2) mediate competitive interactions, and 3) determine the likelihood of mating with other individuals. This might be the case for a trait such as flowering time, which could be subject to stabilizing selection toward some physiologically optimal flowering time, mediate competition for pollinators, and determine the likelihood of mating with other individuals with different flowering time.

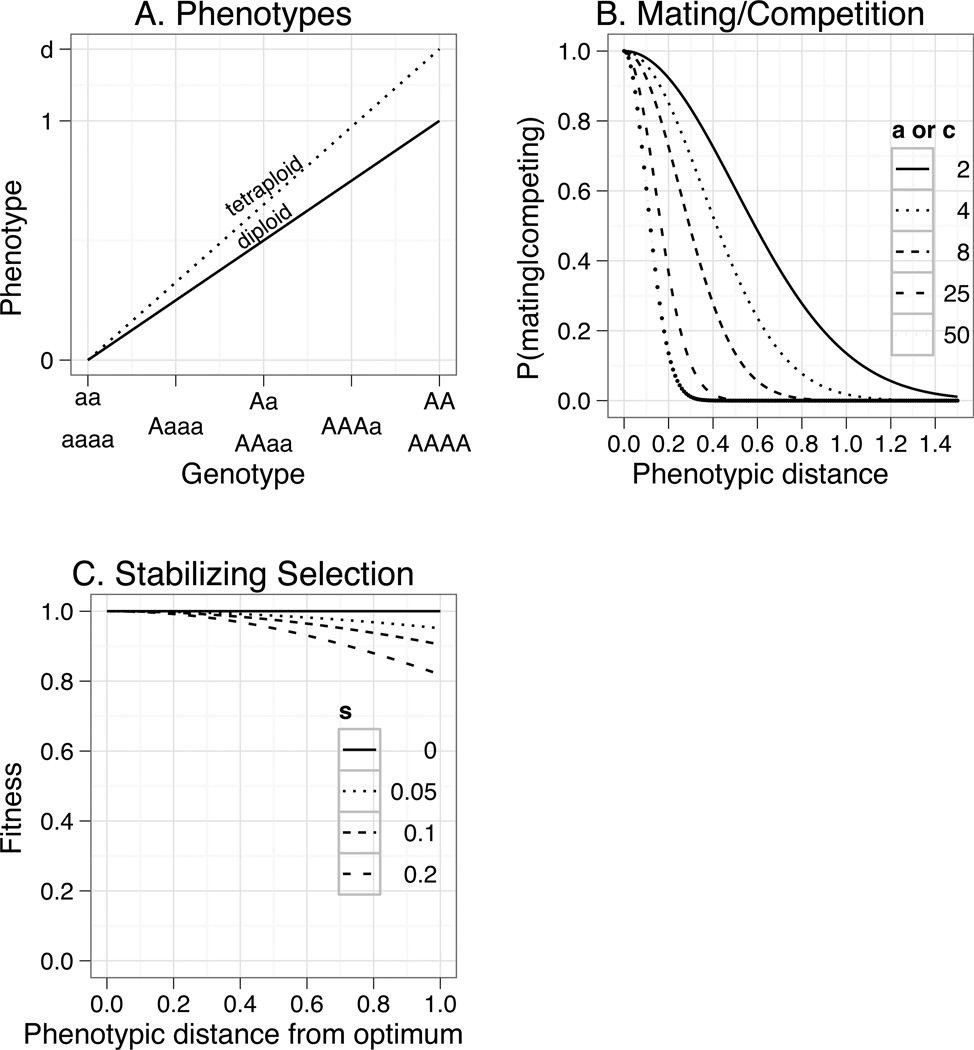
Because tetraploids have twice as many alleles as diploids for a given number of loci, determining the phenotype, p, of an individual in a strictly additive fashion would allow the maximum phenotype of a tetraploid individual to be twice that of a diploid individual. Although this may be the case in some circumstances, the nuances of gene regulation may yield alternative scenarios. To accommodate different mechanisms for gene expression in polyploids (Chen 2007; Osborn et al. 2003), we introduce a parameter d, which lies between one and two (Figure 1A). If d is set to one, the maximum phenotype of a tetraploid individual is equal to that of a diploid individual corresponding to a case of allele-dosage effects without increased phenotypic range (Osborn et al. 2003). If d is set to two, the maximum phenotype of a tetraploid is twice that of a diploid, corresponding to a case of strict additive effects. Intermediate values of d are also plausible where allele-dosage effects do lead to increased phenotypic range or where gene expression is regulated by more complex mechanisms such as gene repression (Chen 2007; Osborn et al. 2003).

Figure 1.

Panel A depicts the phenotypes as a function of the genotypes. In the case of multiple loci, the phenotype for each locus is calculated and averaged with the phenotypes at other loci to form the individuals expressed phenotype. Increasing the number of alleles simply partitions the phenotypic space more finely. Panel B shows the probability of mating with another individual that is a given phenotypic distance away. Since a similar function is used for competition, panel B also depicts the likelihood of competing with another individual that is a given phenotypic distance away. Panel C shows the strength of stabilizing selection for a given phenotypic distance from the optimum.

Within each generation, we assumed that the events of the life cycle proceeded in the following order: 1) population assembly from seeds from the previous generation; 2) stabilizing selection towards an optimal phenotypic value; 3) competition within and between ploidies; and 4) gamete formation and mating within and between ploidies. In the sections below, we provide a detailed explanation of each event in the life cycle.

Population Regulation

The first step in each generation was the assembly of a population of size K from the random selection of seeds from the previous generation. Specifically, a seed was drawn at random from the pool of seeds produced by the previous generation. If the chosen seed was a diploid or tetraploid, it was always added to the population. In contrast, if the chosen seed was a triploid, it was added to the population with probability t <=1 allowing us to model cases of reduced triploid viability.

Stabilizing Selection

Following population regulation, stabilizing selection was assumed to act. Stabilizing selection is thought to be an important explanation for many long term evolutionary patterns (Estes and Arnold 2007), though its frequency and intensity within natural populations remains somewhat uncertain (Kingsolver et al. 2001). In our model, stabilizing selection reduced each individual’s female fitness in proportion to its phenotypic distance from the optimum, such that:

$$W_i=e^{-s{(P-p_i)}^2}$$ (1)

where p_i is the phenotype of individual i, P is the phenotypic optimum, and the parameter s controls the strength of stabilizing selection. We held the phenotypic optimum constant at a value of P=0.5 in our initial simulations.

Competition

Following stabilizing selection, individuals experienced competition. Competition in both inter-and intra-specific forms has been long recognized to be a significant stress for plants (Craine 2009). In our model we assumed that each cytotype was an equally good competitor, and that the strength of competition was determined by the relative phenotypes of the individuals involved. Each individual competed with h randomly selected individuals in the population, with the focal individual having its female fitness reduced proportionally to its phenotypic distance from the interacting individuals according to:

$$W_i^{\text{'}}=W_i\frac{1}{h}\sum _{j\in H}(1-g{e}^{-c{(P_i-P_j)}^2})$$ (2)

In equation (2), H is a randomly selected subset of the population of size h, and the parameters g and c control the strength of competition (Figure 1B). Dividing by h renders the fitness consequences of competition independent of the number of competing individuals, and thus increasing the value of h simply reduces variance in competition effects. The parameters g and c control the strength of competition. Specifically, c determines the probability that two individuals compete as a function of their phenotypes. When c is zero, the probability of competing is independent of phenotype, but when c is large, an individual effectively competes only with identical phenotypes (Figure 1B). The parameter g determines the fitness consequences of competition when it occurs, and takes values between 0 (competition has no fitness consequences) and 1 (competition eliminates female fitness).

Gamete formation and Mating

We assumed that the phenotypic distance between individuals determined the likelihood of a successful mating between them. This might be the case if the phenotype, p, is a trait like flowering time such that individuals with similar flowering times are more likely to mate with one another than are individuals with dissimilar flowering times (Husband and Sabara 2004; Nuismer and Cunningham 2005; Segraves and Thompson 1999). Specifically, we assume that each individual attempted to mate with M randomly selected individuals, with the probability of a successful mating P(S) given by:

$$P(S)=e^{-a{(P_f-P_m)}^2}$$ (3)

where p_f is the phenotype of the focal female individual, and p_m is the phenotype of the randomly selected male individual, and a determines how "choosy" individuals are with respect to the phenotype of potential mates. Specifically, large values of a mean that individuals mate only with individuals whose phenotype is very similar to their own; small values of a mean that individuals mate approximately equally with all individuals, irrespective of their phenotype (Figure 1B). In a successful mating, the focal individual received pollen from the other individual and fertilized one of its ovules.

Within successful matings we assumed that each individual produced gametes in two forms: M ovules, and an effectively unlimited amount of pollen. Each gamete produced was subject to a per chromosome, per locus mutation rate of 1 × 10⁻⁶. Diploid individuals produced unreduced gametes at rate u, and this was the only way for triploids or tetraploids to enter the population. Tetraploid individuals exhibited tetrasomic inheritance and produced only 2× gametes. Triploids produced 2× gametes and 1× gametes in equal proportions.

After all individuals had outcrossed, each individual then self-fertilized any remaining ovules it had with probability r. Mixed mating systems such as this are common (Barrett 2002; Goodwillie et al. 2005; Kalisz et al. 2004; Schemske and Lande 1985), and our model produced selfing rates consistent with published estimates in flowering plants (Barringer 2007; Husband and Schemske 1995) (Supplementary Figure S1). Since outcrossing was included, this reproductive model did not eliminate minority cytotype exclusion, and in the absence of phenotypic diversification would lead to the inevitable extinction of the minority cytotype in all but the smallest of populations.

Finally, fertilized ovules developed into seeds at a rate equal to the focal individual’s female fitness; because we assumed pollen was cheap relative to ovules/seeds (Charnov 1979), individual fitness affected only female fertility. These seeds were stored for the next generation.

Model Parameterization

Due to the number of parameters in the model and the resulting complexity in analysis, we restricted our exploration of parameter space to biologically reasonable values. The rate of unreduced gametes u, was estimated by Ramsey and Schemske (1998) to be 0.0056. Since examples of greater rates of unreduced gamete formation have been reported (Ramsey 2007), and because the rate of unreduced gamete formation can vary considerably with environmental conditions (Otto and Whitton 2000), we used two rates in the simulations, 0.005 and 0.01. Because there are few studies which have estimated the effects of autopolyploidy on gene expression in natural systems (Osborn et al. 2003), we included a wide range of values for the parameter d: 1.1, 1.2, 1.3, 1.5, and 1.7. The sensitivity of mating probabilities to the phenotypes of the individuals could also vary widely, and so we used a broad range of values for the parameter a. These values ranged from zero (equal likelihood of mating regardless of phenotype) to 50 (effectively only mate with your own phenotype) (Figure 1B).

Two parameters, c and g, control the strength of competition and these parameters are also likely to vary substantially among natural systems. For this reason, we used a wide range of values for c (zero to 50) (Figure 1 B) and g (zero to 0.4). Although estimates do exist for the strength of stabilizing selection gradients in natural populations (Kingsolver et al. 2001), little information is available on the values likely taken by the individual stabilizing selection parameter, s, used here. For this reason, we used a range of values for this parameter ranging from zero to 0.2 (Figure 1 C). Finally, we considered triploid viabilities, t, of 0.0, 0.01, 0.05, and 0.1, as these rates are consistent with published estimates (Baack 2005a; Husband 2004; Ramsey and Schemske 1998). With the ranges of the focal parameters established, we performed preliminary simulations that allowed us to trim the non-focal parameter space without losing generality (Supplementary Online Methods).

Sensitivity to environmental fluctuations

Because there is evidence that polyploid lineages may be favored when environmental conditions change rapidly (Fawcett et al. 2009; Parisod et al. 2010), we examined the case of a shifting phenotypic optimum. Simulations proceeded as described above, except that at generation 3000 the phenotypic optimum favored by stabilizing selection, P, was perturbed. Specifically, a new phenotypic optimum was drawn at random from a normal distribution with a mean of 0.5 (the old optimum) and a standard deviation of one, and the old optimum was incrementally shifted to this new value over 100 generations. For a limited subset of parameters (2880 combinations), we evaluated the effect of the magnitude of the random shift by choosing new phenotypic optima from distributions with mean 0.5 and standard deviations of 0.1, 0.5, 1, and 2.

Simulation data set

The majority of the conclusions in this study are based on a set of simulations consisting of 20 replicate simulations lasting 5000 generations for each of 46,080 parameter combinations (Table 1), for a total of 921,600 individual simulations. Additional simulations were performed on more limited parameter sets in order to explore some specific questions (details in supplementary materials and figure legends). Simulations were run on the IBEST supercomputing cluster facilities at the University of Idaho.

Table 1.

Summary of parameters

parameter	description	equation	values
d	gene expression effect, determines the range of phenotypes expressed by tetraploids (Figure 1a)		1.1, 1.2, 1.3, 1.5, 1.7
s	determines both the shape and strength of stabilizing selection (Figure 1c)	1	0, 0.05, 0.1, 0.2
P	phenotypic optimum for stabilizing selection	1	0.5, ∈ N(0.5,1)
c	sensitivity of competition, controls the ange of phenotypes that an individual competes with	2	2, 4, 8, 50
g	strength of competition (Figure1b), determines the affect of competition on fitness	2	0, 0.2, 0.4
h	number of competitors per plant per generation	2	10
a	sensitivity of assortative mating, determines the probability of mating with an individual with a different phenotype (Figure 1b)	3	2, 4, 8, 50
r	rate of reproductive assurance, determines the rate at which unfertilized ovules are self-fertilized		0.85, 0.9, 1.0
M	number of ovules per plant per generation		4
t	triploid viability		0, 0.01, 0.1
K	carrying capacity of the population		1000

Results: Stable Environment

Establishment

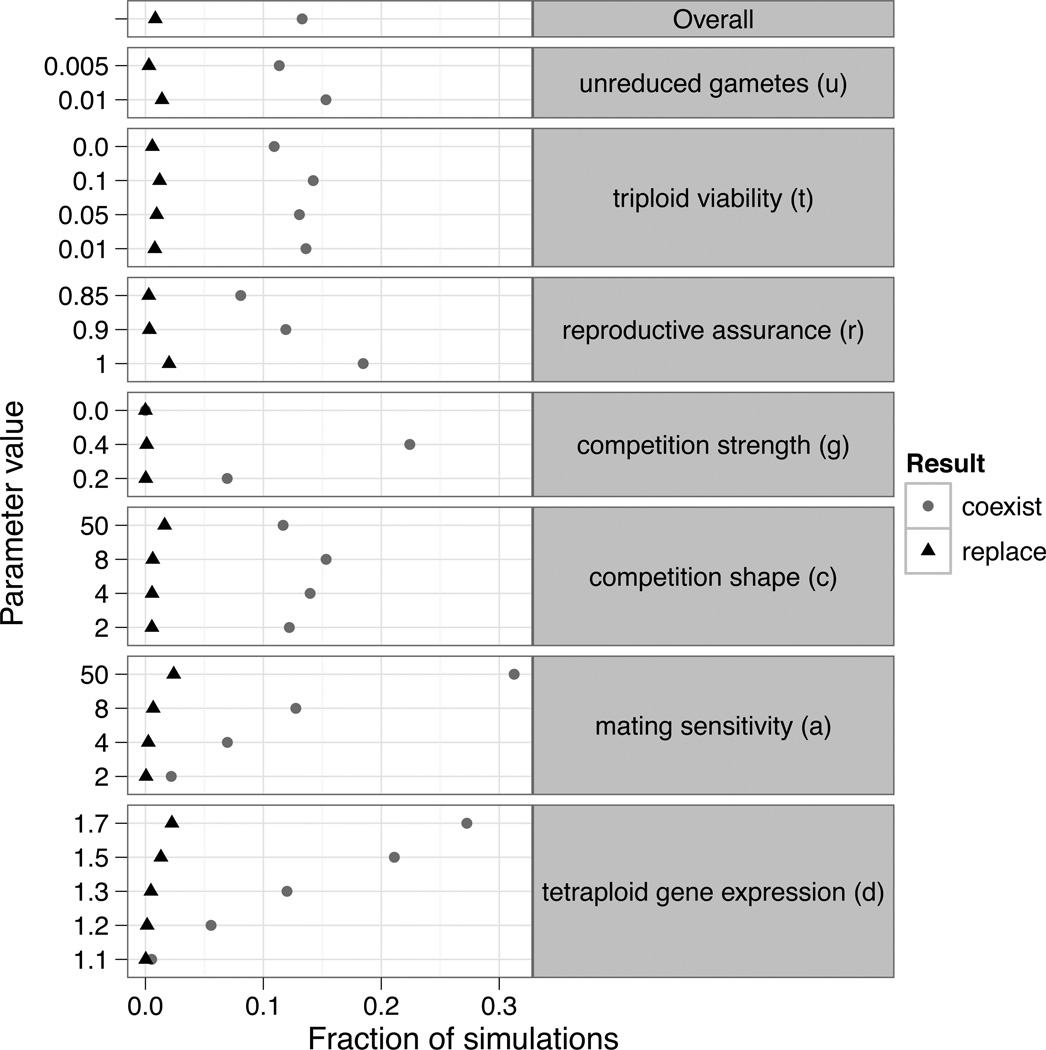
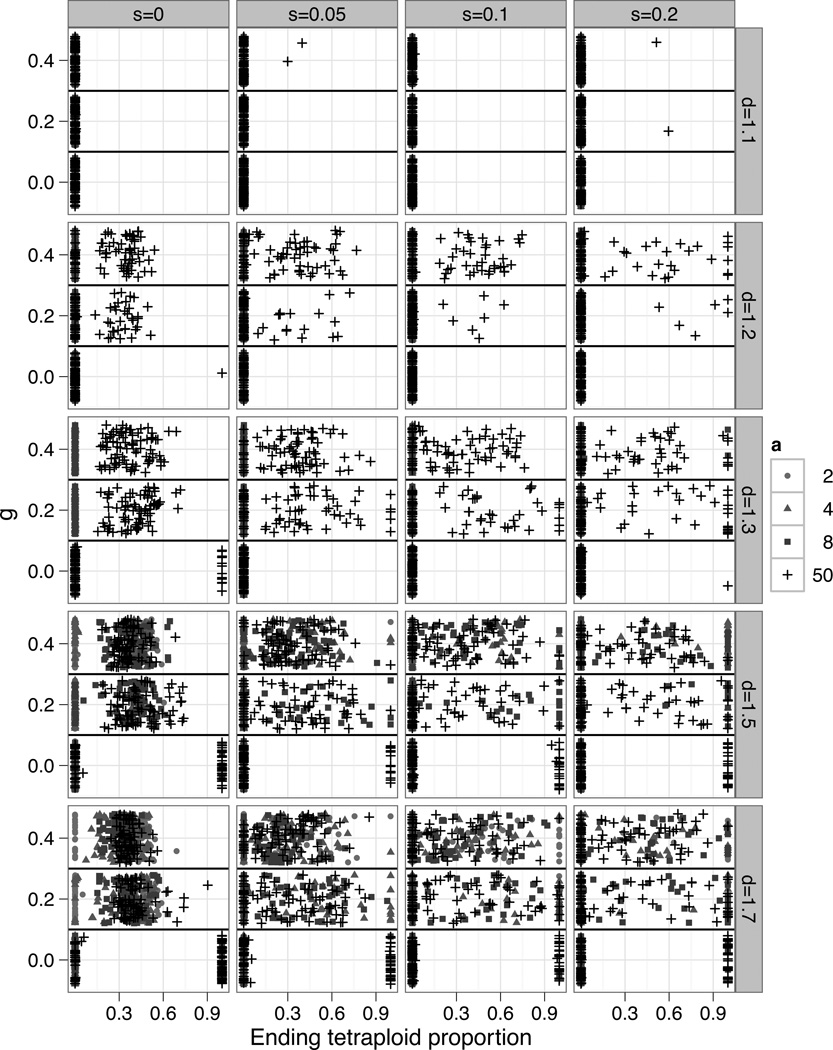
Tetraploid establishment occurred in 13.3% of simulation runs when the phenotypic optimum was stable (Figure 2). Establishment was most likely to occur when the strength of competition and assortative mating depended strongly on individual phenotype (large values of g, and a), because under such conditions, even the evolution of only a small amount of phenotypic divergence allowed the tetraploid population to escape minority cytotype exclusion and competition with diploid progenitors (Figure 3). Establishment was further facilitated by large values of d (d > 1.2), because under such conditions the pattern of gene expression in tetraploids facilitates their evolutionary divergence by allowing tetraploids to achieve greater maximal phenotypes than their diploid progenitors.

Figure 2.

The overall rates of the coexistence of both cytotypes (circles), and replacement of diploids by tetraploids (triangles). For each parameter listed on the right, the fraction of simulations that resulted in each of the possible outcomes is shown for all values of the parameter tested.

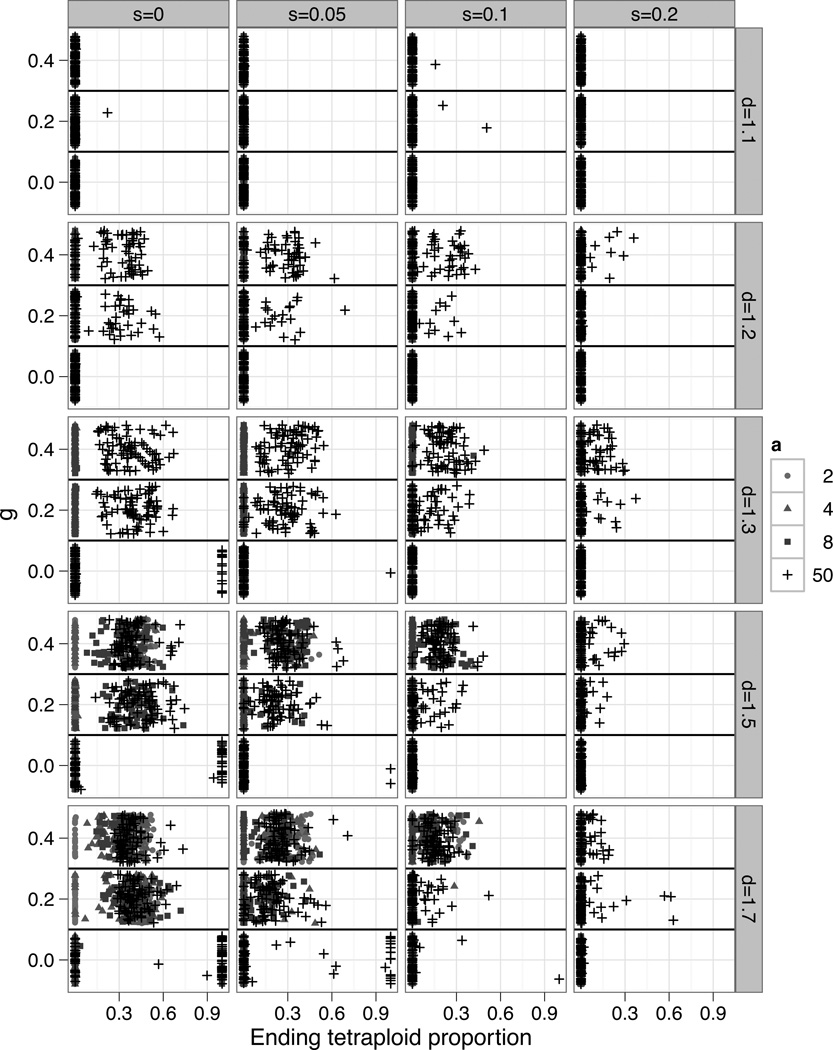
Figure 3.

Each point represents the result of one individual based simulation, with the ending proportion of tetraploids plotted against the parameter g (the affect of competition on fitness). The points are shaded and shaped according to the parameter a, which measures the sensitivity of mating to phenotype. Stabilizing selection (s) increases across horizontal panels. The parameter d, which measures dosage effects, increases across vertical panels. The sensitivity of competition relative to phenotype (c) varied from 2 to 50. Other parameters were fixed (u=0.005, t=0.01, r=1, loci=2, alleles=10, K=1000, P=0.05).

Even in those cases where competition and assortative mating were very sensitive to individual phenotypes (large a and g), and phenotypes of tetraploids were free to diverge (large d), some amount of selfing was also necessary for polyploid establishment. Specifically, establishment was very rarely observed for values of r below 0.6 and increasing values of r increased the probability of establishment (Supplementary Figure S4), and the rate of realized selfing (Supplementary Figure S5).

Relative to the strong effects of competition, assortative mating, and gene expression, the rate of unreduced gamete formation (u) and the viability of triploids (t) had weaker effects on polyploid establishment (Figure 2). Specifically, increasing the effects of competition on fitness (g) increased the probability of establishment by 27% and increasing a from 2 to 50 resulted in 29% increase in the probability of establishment. In contrast, the probability of polyploid establishment was only 4% higher when the rate of unreduced gamete formation was 0.01 rather than 0.005. Similarly, the probability of establishment was only increased by 0.6% when triploid viability was increased from 0.01 to 0.1.

Coexistence

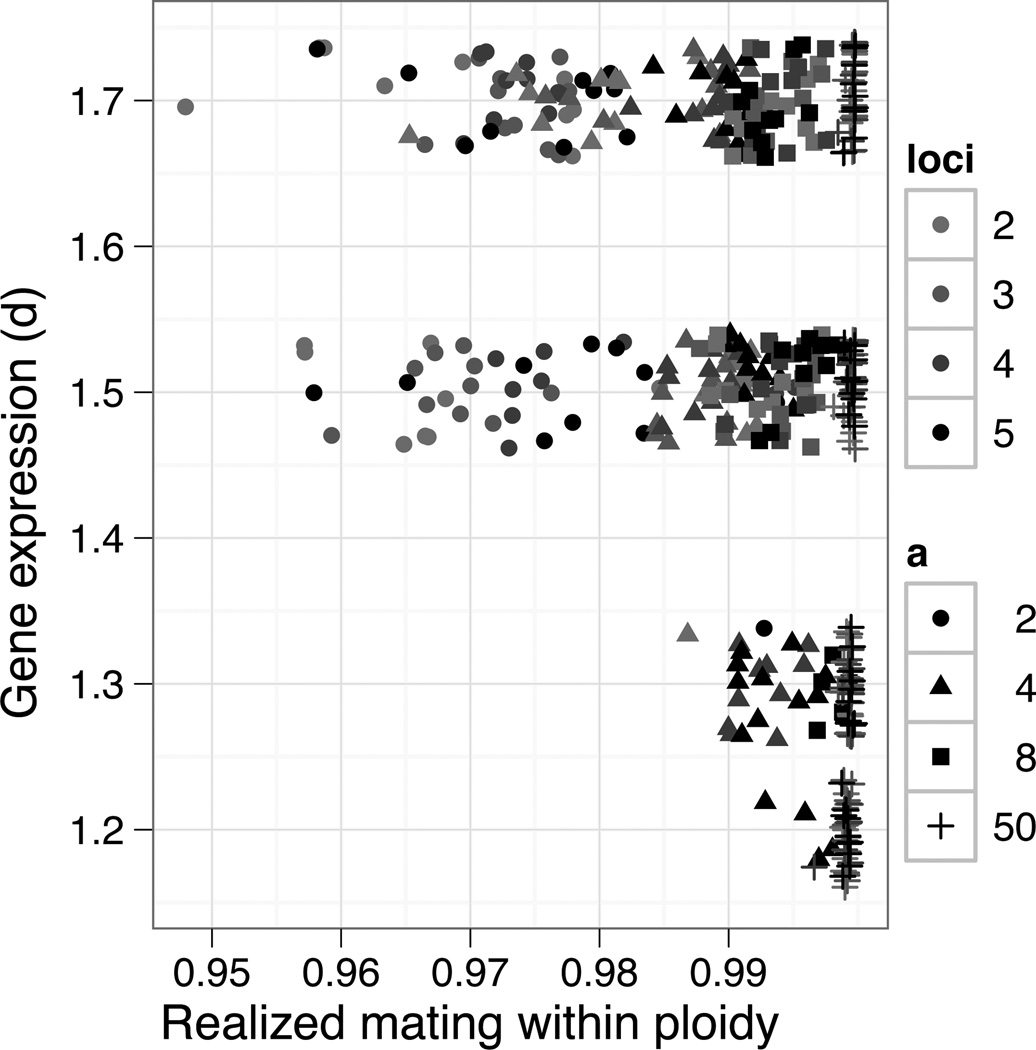
When polyploids became established, they generally coexisted in sympatry with their diploid progenitors (Figure 3). Specifically, of the 13.3% of cases where polyploids became successfully established, coexistence occurred with diploids in 93.2% of cases. Coexistence was most frequent when stabilizing selection was absent or weak, and when d was large. In these cases, tetraploids escaped minority cytotype exclusion by evolving phenotypes sufficiently divergent from their diploid progenitors for assortative mating to be nearly complete (prezygotic isolation >95%, Figure 4). This is very similar to values of prezygotic isolation observed in Chamerion angustifolium (97.6%) (Husband and Sabara 2004), and somewhat higher than in Heuchera grossulariifolia (85%) (Nuismer unpublished).

Figure 4.

Each point represents the average realized rate of assortative mating within ploidy over the course of a simulation for the given values of d. Points are only shown for simulations that resulted in coexistence of diploids and tetraploids. Other parameters were fixed (c=4, g=0.4, u=0.01).

In contrast, when stabilizing selection was present and d small, tetraploid phenotypes were so constrained that substantial divergence from their diploid progenitors generally failed to evolve. Under such conditions, coexistence required that assortative mating and competition be very sensitive to differences in individual phenotypes such that tetraploids could escape competition and MCE with only slightly divergent phenotypes.

Replacement

In a constant abiotic environment, tetraploids replaced diploids in only 0.9% of total simulations, or 6.8% of cases where the tetraploid was able to establish. All of these cases were characterized by an absence of competition. When stabilizing selection was weak and competition absent, the tetraploids were able to replace the diploids if assortative mating was very sensitive to differences in individual phenotypes. This was possible due to the constant formation of unreduced gametes and little intercytotype mating. However, even a moderate amount of stabilizing selection prevents replacement except a few cases when d was large (d = 1.7). Replacement of the diploid population was also limited by d itself, with tetraploids never replacing the diploids when d was less than 1.3.

Results: Shifting optimum

When the optimum phenotype favored by stabilizing selection shifted, the rate of tetraploid establishment remained similar to the case of a constant abiotic environment. Specifically, tetraploids established in 14.1% of simulations. Although the overall rate of tetraploid establishment did not differ, it did allow a broader range of parameters to result in the coexistence of cytotypes (Figure 5). In addition to having little effect on the rate of polyploid establishment, environmental change had only a very slight effect on the overall rate of coexistence, with coexistence occurring in 11.4% of simulations.

Figure 5.

Each point represents the result of one individual based simulation, with the ending proportion of tetraploids plotted against the parameter g (the affect of competition on fitness). In this case the phenotypic optimum P was shifted at generation 3000 during the simulation. The new phenotypic optimum was randomly sampled from a normal distribution with mean 0.5 and standard deviation of one. The points are shaded and shaped according to the parameter a, which measures the sensitivity of mating to phenotype. Stabilizing selection (s) increases across horizontal panels. The parameter d, which measures dosage effects, increases across vertical panels. The sensitivity of competition relative to phenotype (c) varied from 2 to 50. Other parameters were fixed (u=0.005, t=0.01, r=1, loci=2, alleles=10, K=1000).

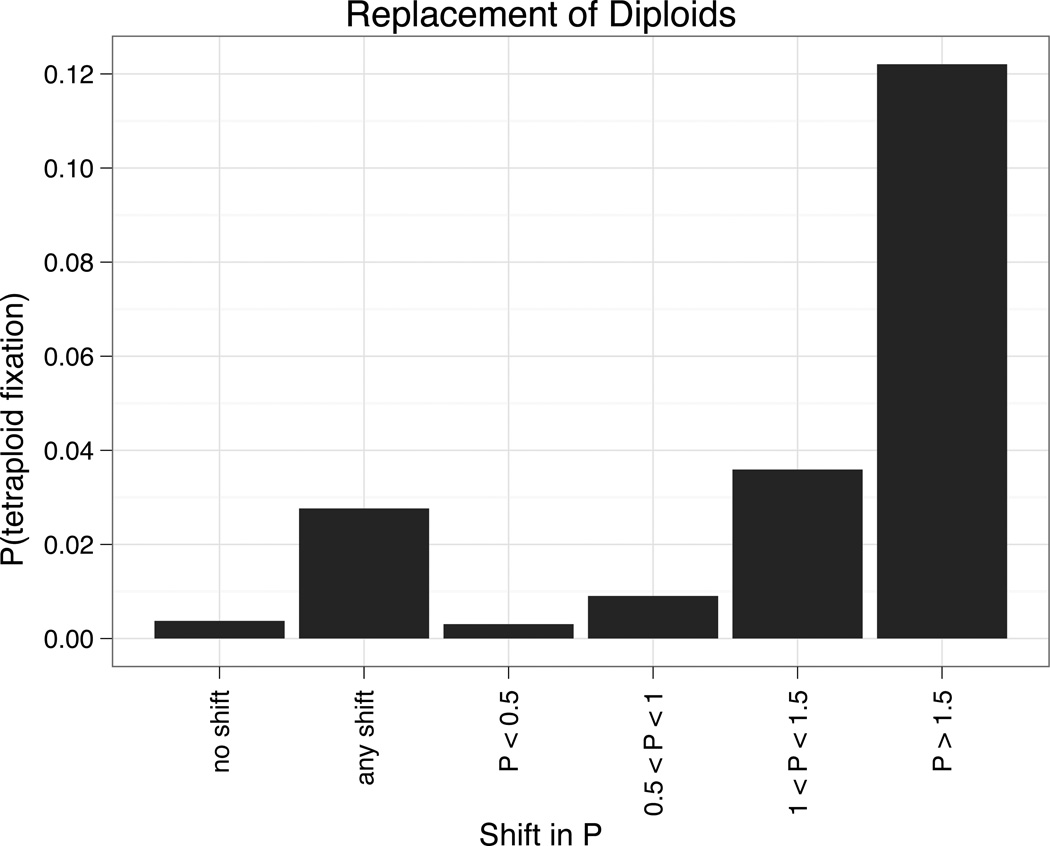
Although our simulations revealed that rates of polyploid establishment and coexistence were similar in both constant and changing environments, replacement of diploids by tetraploids was much more likely when the environment changed. Specifically, in those simulations where the environment shifted, tetraploids replaced diploids in 2.6% of all simulations and 18.4 % of simulations where tetraploids established (Figure 6). Thus, replacement of diploids by tetraploids was twice as likely in a shifting environment as in a constant one. As expected, the more the optimum shifted in the direction of tetraploid divergence, the greater the probability of tetraploid replacement, though any shift in the optimum at all lead to more frequent replacement. In addition, when larger environmental shifts were considered (by increasing the variance of the distribution from which new phenotypic optima were drawn) tetraploids replaced the diploids with higher frequency (Supplementary Figure S6).

Figure 6.

Each bar represents the proportion of individual based simulations (over all parameter combinations) where the tetraploids established and replaced diploids. The shifted phenotypic optimum P was randomly drawn from a normal distribution with a mean of 0.5 and a standard deviation of one.

Although the rate of unreduced gamete formation had only a weak effect in a constant environment, this is not the case when the environment changes. Specifically, the rate of unreduced gametes had a much stronger effect on the probability of tetraploid fixation because when the optimum shifted, the tetraploids may not have composed a significant portion of the population. In such cases, the increased rate of formation made it more likely that tetraploids formed in time to capitalize on advantageous shifts in the phenotypic optimum. Supplementary Figure S7 depicts the results of one example simulation where the phenotypic optimum was shifted in the direction of tetraploid divergence and resulted i n replacement of the diploid population.

Discussion

Whether polyploidy is just a common mutation that can lead to distinct lineages or whether it directly promotes diversification through increased adaptability remains an open question (Otto 2007). These two views could be seen as opposite ends of a spectrum of possibilities, and neither extreme view is likely to be correct for all polyploid taxa. Our results support the idea that polyploids do not need to be more adaptable to explain their prevalence. We found that a polyploid lineage needs no distinct advantages in order to establish within a diploid population and coexist stably. We also found that when there is a shifting phenotypic optimum, polyploids can occasionally replace their diploid progenitors. During periods of rapid environmental changes such as the Cretaceous-Tertiary extinction (Fawcett et al. 2009), or retreating glaciers (Brochmann et al. 2004), polyploids may have survived and replaced their diploid ancestors simply because of their divergent phenotypes, which by chance were closer to the shifting phenotypic optima of the time. No special properties of genomic duplication per se need to be invoked.

Establishment

In general we found that neopolyploid establishment will occur with much higher probability than previous models predicted. Whereas previous models predicted that the rate of formation of polyploids was key to their establishment (Felber 1991), we found that rates of formation were not the primary factor determining whether the tetraploid lineage was successful in becoming established. Specifically, our results demonstrate that the rate of unreduced gametes, and the viability of triploids, which both affect the rate of formation of neopolyploids, are of secondary importance. In contrast, our results show that the most important factors influencing whether or not polyploids establish are the effects of dosage in gene expression of neopolyploids (d), and the sensitivity of competition and assortative mating to phenotype (a, g).

Although our results contradict previous work with regard to the importance of unreduced gamete formation and triploid viability, they support work suggesting that reproductive assurance is important for polyploid establishment (Otto 2007; Otto and Whitton 2000). When the first few neopolyploids were formed from the diploid population, their likelihood of successfully outcrossing with the diploids was relatively small, which caused them to reproduce through self-fertilization. As soon as a small number of neopolyploids formed, their realized rate of selfing dropped to the levels found in the diploid (Figure 7c). Previous models have also found that selfing aids, and may even be necessary for, neopolyploid establishment (Rausch et al. 2005; Rodriguez 1996).

In general our model is conservative in estimating the evolutionary success of polyploids, as there are additional factors that may aid tetraploid establishment that we do not include in our model. For example, pure selfing or vegetative reproduction would further enhance the likelihood of the polyploid lineage establishing (Otto and Whitton 2000), though the long term consequences of selfing, such as inbreeding depression, may limit the evolutionary success of these polyploids. Iteroparity would also likely benefit the polyploid lineage, allowing a small population to persist longer while awaiting the formation of another polyploid (Otto and Whitton 2000). Spatially distributed populations would also benefit neopolyploid establishment, by allowing pockets of polyploids to form and increase assortative mating (Baack 2005b). Additionally, smaller population sizes have been found to favor polyploid establishment (Rausch et al. 2005). Finally, fitness advantages such as increased resistance to pathogens (Oswald and Nuismer 2007), would further increase the likelihood of polyploid establishment. Taken individually, each of these possible mechanisms is unable to overcome the minority cytotype disadvantage, but in combination with the model described here, a compelling case for establishment can be made.

Coexistence

Competition, both inter-and intra-cytotype, is a key component in coexistence between cytotypes. Intercytotype competition based on phenotype causes the two ploidies to evolve into slightly different niches, and thus facilitates assortative mating. Because, intercytotype matings produce largely inviable triploids, reinforcement for mating within ploidy occurs as well. Together competition and reinforcement lead to divergence and coexistence of the diploid and tetraploid lineages. Two previous models found that a polyploid lineage and its diploid progenitor could coexist (Fowler and Levin 1984; Rodriguez 1996). Both of these previous models were competition models that treated the diploids and polyploids as separate species with a fixed amount of niche overlap. Using classical competition models such as these can make parameter estimation and empirical testing difficult. In addition, Fowler and Levin (1984) gave the polyploid species a competitive advantage that is not required in our model. When both ploidies coexisted, we found rates of assortative mating within cytotype to be relatively high, indicating each ploidy was essentially a species. This rate of assortative mating is quite similar to the rate of assortative mating observed in tetraploid Chamerion angustifolium (Husband and Sabara 2004), suggesting our model is parameterized correctly.

Replacement

Our model also predicts that replacement of the diploid ancestor by neopolyploids should in general be quite rare, with coexistence being much more likely. This may explain why most angiosperms have a polyploidization event in their evolutionary history (Masterson 1994), yet do not appear to diversify at greater rates (Wood et al. 2009) as would be expected from increased adaptability. Our model suggests that there is a “right place at the right time” effect of polyploidy, that is: most of the time there is little to no advantage for polyploids, but occasionally, when the environment changes rapidly, polyploid lineages may have an evolutionary advantage. This is consistent with the observation that many polyploid events date to the time of the Cretaceous-Tertiary extinction (Fawcett et al. 2009), and with the observation that polyploids may be favored when the environment changes rapidly (Parisod et al. 2010).

Conclusion

Through extensive exploration of a wide parameter space we have found that the establishment of neopolyploid lineages is not dependent on any fitness advantages that may or may not be characteristic of polyploids. Instead, we find that the evolution of phenotypic divergence, in conjunction with moderate levels of reproductive assurance allow neopolyploids to establish themselves, coexist with their diploid progenitors, and sometimes replace them. During periods of environmental change, such as the Cretaceous-Tertiary extinction and possibly our current state of global climate change, polyploid lineages are even more likely to be favored.