PhosphoChain: a novel algorithm to predict kinase and phosphatase networks from high-throughput expression data

Abstract

Motivation: Protein phosphorylation is critical for regulating cellular activities by controlling protein activities, localization and turnover, and by transmitting information within cells through signaling networks. However, predictions of protein phosphorylation and signaling networks remain a significant challenge, lagging behind predictions of transcriptional regulatory networks into which they often feed.

Results: We developed PhosphoChain to predict kinases, phosphatases and chains of phosphorylation events in signaling networks by combining mRNA expression levels of regulators and targets with a motif detection algorithm and optional prior information. PhosphoChain correctly reconstructed ∼78% of the yeast mitogen-activated protein kinase pathway from publicly available data. When tested on yeast phosphoproteomic data from large-scale mass spectrometry experiments, PhosphoChain correctly identified ∼27% more phosphorylation sites than existing motif detection tools (NetPhosYeast and GPS2.0), and predictions of kinase–phosphatase interactions overlapped with ∼59% of known interactions present in yeast databases. PhosphoChain provides a valuable framework for predicting condition-specific phosphorylation events from high-throughput data.

Availability: PhosphoChain is implemented in Java and available at http://virgo.csie.ncku.edu.tw/PhosphoChain/ or http://aitchisonlab.com/PhosphoChain

Contact: john.aitchison@systemsbiology.org or jchiang@mail.ncku.edu.tw

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Protein post-translational modifications (PTMs) enable proteins to rapidly switch from one state to another. Signaling networks exploit this feature to transmit information from the cytoplasm and outside the cell to the genome by interfacing with transcription factors, which themselves form complex gene regulatory networks. In comparison with gene regulatory networks, our understanding and prediction of signaling networks is undeveloped, yet critical to a systems view of complex regulatory dynamics.

Protein phosphorylation is by far the most commonly studied and predominant post-translational modification of signaling networks. Moreover, phosphorylation of signaling proteins is fundamental to cellular responses, health and disease (Gotz et al., 2010; van Berlo et al., 2011). Kinases and phosphatases, which are responsible for adding and removing phosphates from proteins, are common drug targets (Imming et al., 2006).

The vast majority of existing tools for predicting phosphorylation events tend to focus on predicting phosphorylation sites from amino acid sequences (Ingrell et al., 2007; Xue et al., 2008). This approach is limited because kinases and phosphatases tend to act on many of the same sites, and thus it is not clear which factors are active under which conditions (Schwartz and Madhani, 2004; Stark et al., 2010). Therefore, we sought to include activity data to improve the predictability of phosphorylation events and to reconstruct signaling networks.

Studies of signaling networks in both yeast (Prinz et al., 2004; Roberts et al., 2000) and mammalian (Avignon et al., 1995; Kusari et al., 1997) cells reveal that the expression of genes encoding kinases often increases with the activation of the signaling pathway, suggesting that expression might be a predictor of signaling network activities. Similarly, high-throughput phosphoproteomics studies using biochemical enrichment and mass spectrometry have led to large experimentally validated proteomic databases annotating phosphorylation on target proteins (Khoury et al., 2011). These data map the potential changes of protein activities and can be used to predict new phosphorylation events and phosphorylation-driven regulatory networks.

Therefore, we developed a tool, called PhosphoChain, which includes condition-specific regulatory information (i.e. kinase and phosphatase activities or proxies thereof) to predict PTM regulatory events and signaling network activities. In comparison with 70 other phosphorylation prediction tools (Supplementary Table S1), only RegPhos (Lee et al., 2011) and HeR Module (Wang et al., 2012) included activity data, and RegPhos only used it to verify their predictions.

PhosphoChain works by constructing an alternating decision tree (ADTree) containing nodes that predict whether a kinase or phosphatase is active as well as the activities of target proteins based on protein activity patterns and phosphorylation sequence motifs that occur in multiple experiments. Here, we apply PhosphoChain to the yeast MAPK (mitogen-activated protein kinase) network as a test case and on a genome-wide scale to predict the entire kinase-phosphatase-transcription factor regulatory network in yeast. The decision tree provides three biologically relevant predictions: (i) given the measured activity for a few factors, it predicts the activity levels for many targets; (ii) it predicts the target sequence for factors (kinases or phosphatases); and (iii) it predicts the chain of post-translational modifications (such as in the MAPK pathway) that are responsible for downstream transcriptional changes.

2 METHODS

PhosphoChain builds a post-translational modification regulatory network by constructing an ADTree (Freund and Mason, 1999) for each target protein in a genome or subset thereof. It is based on the Motif Element Discrimination Using Sequence Agglomeration (MEDUSA) algorithm (Bozdag et al., 2010; Kundaje et al., 2008), a tool that combines mRNA expression with transcription factor binding motifs to predict gene expression. MEDUSA is a highly accurate regulatory network detection tool that identifies regulation by simultaneously considering transcription factor (TF) mRNA expression events, target gene mRNA expression events and the existence of a TF binding motif on the target genes. We developed PhosphoChain by modifying the core MEDUSA concepts to detect post-translational modification events. Specifically, we simultaneously consider post-translational modification factor activation events, target protein activation events and the existence of a factor binding motif on the target protein. We augment this with an optional prior association matrix based on gene deletion studies, a concept borrowed from the HeR algorithm (Wang et al., 2012).

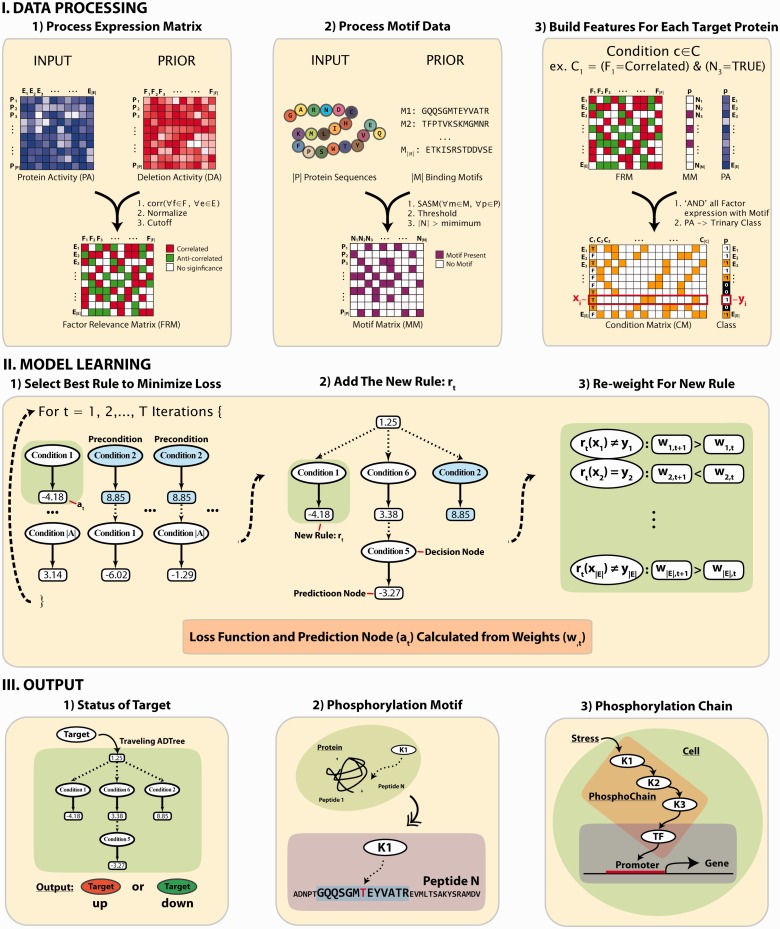
As shown in Figure 1, PhosphoChain combines the input protein activity (PA) data with prior information to generate two sets of features: a factor relevance matrix (FRM) and a motif matrix (MM). FRM is calculated using the Pearson correlation coefficient (PCC) between the experimental activity data and a prior activity matrix consisting of mutants with the genes encoding the protein factors (e.g. kinases/phosphatases) deleted (van Wageningen et al., 2010). In this way, prior information from factor deletions is taken into consideration to favorably weight known relationships among factors and targets. If a factor deletion matrix is unavailable, then PhosphoChain will use the input PA matrix directly instead of the FRM. The MM contains a set of candidate peptide motifs calculated based on the similarity to known phosphorylation motifs (Stark et al., 2010) as measured by an amino acid similarity matrix, structural similarity matrix (SASM) (Goonesekere, 2009), which is a structure-derived matrix used for detecting protein homologs. All possible pairs consisting of FRM and MM features are combined to create condition matrix (CM). Descriptions of variables are shown in Supplementary Table S2.

Fig. 1.

Overall strategy to identify phosphorylation network for PhosphoChain. DATA PROCESSING: PhosphoChain constructs three matrices from the input data to generate the model: an FRM, a binding MM and a CM. FRM is calculated using the PCC between the input PA profile and factor DA profile. MM is generated from a list of template peptide motifs calculated based on the similarity to known phosphorylation motifs as measured by the structure-derived amino acid substitution matrix, SASM. CM is generated by combining the FRM and MM. MODEL LEARNING: For each target protein, an ADTree composed of decision nodes and prediction nodes is generated from the CM. Decision nodes specify the predicate condition that (i) the kinase/phosphatase has a high correlation/anti-correlation with the experiment; and (ii) the phosphorylated motif is present on the protein sequence. Each prediction node contains a score associated with a decision node. By traversing all satisfied nodes on the ADTree, target activity is predicted. OUTPUT: The PhosphoChain model predicts (i) target activity; (ii) phosphorylation sites; and (iii) protein phosphorylation chains

To learn the PhosphoChain model, we try to predict the class (i.e. the activity level: +1 or −1) of each target protein from the CM by generating an ADTree. The ADTree is composed of decision nodes and prediction nodes. Decision nodes specify the predicate condition that (i) the factor has a significant correlation/anti-correlation in the FRM, and (ii) the phosphorylated motif is present on the target protein sequence in the MM. Prediction nodes contain a score associated with decision node. The final network is generated by traversing all nodes in the final ADTree. Once completed, the PhosphoChain model provides three contributions: (i) a predicted class for a target protein, (ii) a predicted factor binding site on the target protein and (iii) a predicted chain of phosphorylation events.

Figure 1 and Supplementary Table S2 provide additional information that is intended to make the PhosphoChain algorithm as clear as possible.

2.1 Datasets used to predict MAPK networks

We used two lists of factors considered as possible regulators when testing out PhosphoChain: (i) the kinase/phosphatase (KP) dataset contained 144 factors deleted by (van Wageningen et al., 2010), and (ii) the kinase/phosphatase/transcription factor (KPT) dataset contained 345 factors. This list contained 233 kinases/phosphatases and associated proteins taken from yeast kinome (Breitkreutz et al., 2010; van Wageningen et al., 2010) and 112 TFs from YEASTRACT (Abdulrehman et al., 2011).

2.2 Data processing

PhosphoChain takes as input a matrix of expressed PA for a set of proteins 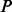across a set of experiments 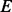(e.g. mRNA expression experiments). Each protein 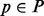is associated with a protein sequence s ∈ S. These input data are paired with prior information. The PA is paired with a deletion activity (DA) matrix containing activity levels for proteins that include 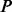in experiments where factors f ∈ F are perturbed. The protein sequences 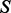are scored against known phosphorylation motifs .

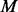2.2.1 Identification of FRM

In this study, the PA matrix for PhosphoChain is based on the mRNA expression. These datasets are noisy, and the information relevant to PTMs may be masked by larger signals. Therefore, it was desirable to weight the input matrix so that known relationships among modifiers and targets are enhanced. As shown in Figure 1, panel I.1, the FRM makes this possible. Input data are transformed into the FRM by calculating the PCC between a DA matrix (van Wageningen et al., 2010) and the PA matrix:

where 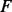contains protein factors for which genes are deleted in mutants, and the 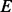denotes experiments in which the activity profiles are measured. Positive 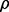s are normalized by

Negative 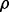s are normalized by

To include only significantly correlated kinases/phosphatases in the FRM, we quantized using a threshold of 0.3. Thus, the FRM becomes trinary according to the following logic:

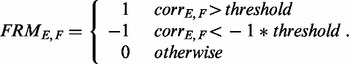2.2.2 Identification of factor binding MM

PhosphoChain generates a set of new template binding motifs N from the set of known phosphorylation motifs 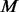[as reported by PhosphoGRID (Stark et al., 2010)] and the set of protein sequence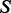s . As 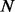is calculated using a SASM-based similarity score matrix on the known motifs, it may contain ‘new’ binding motifs, similar to protein binding sequences that have not yet been observed. SASM is a structure-based substitution matrix for detecting protein homologs that is expected to be more accurate for our purposes than BLOSUM62 (Goonesekere, 2009). The similarity is calculated as:

where s is a k-mer (a k length peptide) generated from a protein sequence using a sliding window. Our scheme more heavily weights those residues closest to the center (i.e. modified) residue. By default, we use k = 13, where the 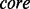is within +/− 3 residues from the center, and the side is the remaining six residues (Supplementary Fig. S1 for a visualization). The parameter weights how important the current core fragment is relative to the side. Here, 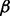is set to 0.9 as shown in Supplementary Figure S2. To generate candidate motifs, the similarity score matrix is quantized using the following criteria:

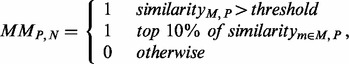where threshold is set to 0.5 to make sure the model has good generalization. Similarly, the 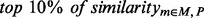provides an alternative criteria to ensure that 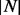is sufficiently large.

2.2.3 Identification of CM

PhosphoChain generates rules with the following form: if factor f ∈ F is correlated and motif n ∈ N is present, then f affects a target protein p. These rules create a binary CM containing all pairs of correlations f and motifs n for all experiments E. The CM is associated a class vector (protein activities rounded to +1, 0 or −1) as shown in Figure 1, panel I.3. The CM combined with the class vector creates a canonical feature matrix with feature vector/class pairs 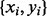, where 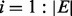and is the number of experiments in the input PA matrix. Thus 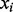refers to a row in the CM, and 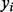refers to the activity of 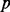in experiment . Because CM is generally sparse and the PhosphoChain algorithm does not consider experiments where y_i = 0, x_i and y_i are calculated on the fly directly from the FRM and MM as well as a pre-trinarized PA matrix.

2.3 Model learning

PhosphoChain constructs an ADTree to predict the activity level for each target protein p ∈ P. The detailed pseudo-code for the PhosphoChain is presented below and in Figure 1, panel II. In this study, we ran the algorithm for 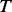iterations, where 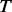is approximately 2.5 times the number of kinases/phosphatases in the set of factors F.

Initialization:

PhosphoChain extracts training data from the CM as inputs {x_i, y_i}, where 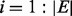. As previously stated, x_i is a condition vector drawn from a row of the CM, and y_i is the activity level of the target protein in those experiments where it significantly changes (rounded to −1 or 1). Experiments where the target PA does not significantly change are excluded from consideration, and the algorithm is initialized as follows:

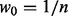• , where w is matrix of weights.

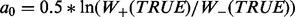• , where a is set of prediction values, 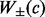is sum of the weights of all positively (+) and negatively (−) labeled examples that satisfy condition c.

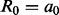• , where R is a set of rules, R₀ refers to root in the ADTree. A rule 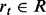consists of zero or more condition nodes and one or more prediction nodes containing values such as a₀.

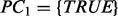• , where PC is a set of preconditions associated with the rules R.

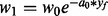• , re-adjust weights.

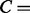• conditions corresponding to the columns in the CM.

Execution:

• For

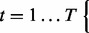
  1. Generate preconditions 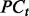from the current rules .
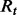  2. For each precondition 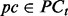and each condition 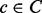, determine the c and p that minimize the boosting loss function:

     
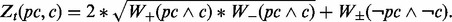
  3. Given the pc and c that minimize Z_t (pc, c), create the new rule set: 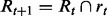, where r_t is a rule with precondition pc, condition c and prediction value a_t such that

     
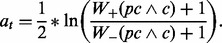
  4. Update weights such that

     

     where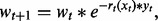 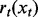is the predicted activity for the current protein based on the new rule r_t and the condition-specific truth values in x_t. //End for loop.

Although each target protein may be correctly said to have its own ADTree, this algorithm computes all such ADTrees simultaneously. Thus, all ADTrees share a common head node, and ADTrees for proteins that have a particular binding motif will share common nodes with that motif.

Output:

PhosphoChain makes three predictions as outlined in Figure 1, panel III: (i) the predicted activity for each protein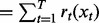; (ii) the binding sequences on that protein; and (iii) the regulatory network for that target protein. To traverse the ADTree and reconstruct the network, PhosphoChain uses PA values that may be part of the PA or may come from new experimental data. PhosphoChain evaluates the activity-based preconditions specified in the decision node. If the tree for p contains a satisfied decision node specifying factor f and motif n, then we say that f binds to p at the residues in protein sequence s that most closely matches n. Finally, we determine whether the binding of f activates or deactivates p in a given experiment e by evaluating the activity levels of f and p. If f is activated and p is activated, then f activates p. If f is activated and p is deactivated, then f deactivates p. Similarly, if f is deactivated and p is activated, then we say that f deactivates p. If f is deactivated and p is deactivated, then we say that f activates p. Thus, the PhosphoChain ADTree structure allows a factor to activate or deactivate the same target depending on the available data. Once regulation is determined for all proteins (e.g. A activates B, B deactivates C), then these can be chained into a network (e.g. A activates B deactivates C).

2.3.1 Scoring the models

To score models using the undirected graph, we counted all known relationships between factors as an edge, and scored based on the percentage of edges correctly predicted by the model. To score models using the directed graph, we counted it as a correct answer if the model correctly identified an activating/deactivating relationship and an incorrect answer if such a relationship was missed. For example, if X was known to activate Y, it would count as wrong if a model found that X interacts with or deactivates Y. If a relationship was known to exist, but no direction (i.e. activation/deactivation) was known, then an activation, deactivation or relationship with no direction predicted was counted as a correct answer; the answer was counted as wrong only if the relationship was missed entirely (see the scoring scheme in Supplementary Table S3). The MAPK pathway presented here was taken from the Kyoto Encyclopedia of Genes and Genomes (KEGG) database and previous studies (see Supplementary Table S4). P-values were calculated using a binomial test.

To estimate an upper bound on the false discovery rate (FDR), we assume that interactions between factors that do not appear in the literature do not exist. In specific, we treat each of the three MAPK sections presented in Figure 2 as an independent entity. If a model predicts an interaction between factors within these MAPK sections and no interaction exists in the literature, we count that as a false positive (e.g. if a model predicts that Hog1 activates Ptp3). As an alternative method, we estimate the false positive rate (FPR) by repeatedly shuffling the training data and then building a model of the MAPK pathway. Known relationships that match the model are counted as false positives; known relationships that do not match are counted as true negatives.

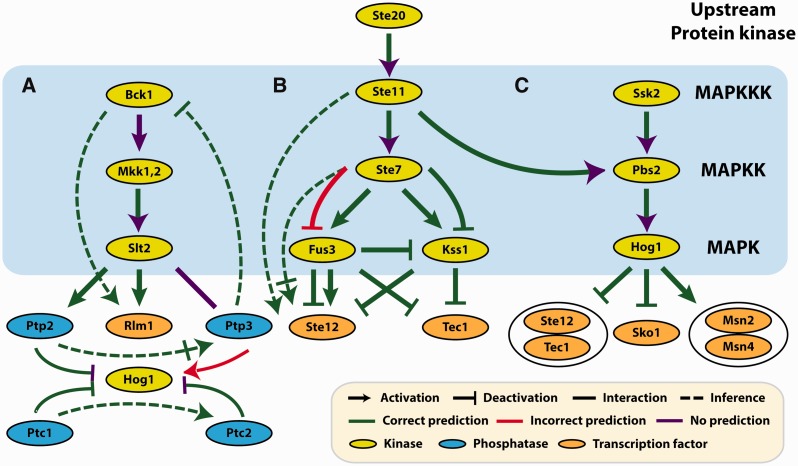
Fig. 2.

PhosphoChain MAPK reconstruction. The MAPK pathway separated into (A) the Bck1-Slt2 and Hog1 pathways, (B) the Ste20-Fus3 and Ste20-Kss1 pathways and (C) the Ssk2-Hog1 pathway. A dashed green line means that PhosphoChain predicts a known undirected interaction to be activation or deactivation. A solid green line with a purple arrowhead means that PhosphoChain predicts an interaction with no direction. These predicted interactions are the same regardless of whether or not the GRA algorithm (Section 2.3.2) is run

2.3.2 Greedy reduction algorithm

PhosphoChain decision trees simultaneously include predictions for all conditions represented in the training set resulting in many predictions. To remove less likely KPT interaction predictions, we implemented a greedy reduction algorithm (GRA) to reduce the number of predictions. If an ADTree can produce correct predictions using only known protein–protein interactions (PPIs), then all novel PPIs are excluded. However, if the novel interactions are necessary for a good prediction, then they are left in. GRA runs as follows:

• For p ∈ P {

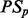•    = Prediction node scores taken from the ADTree built for p.

•   Class_p  = The trinary class vector for protein p.

•   Sort PS_p so the smallest contributing factors are first.

•   For f ∈ factors in PS_p that are not known to interact with p {

•     Calculate PS′ omitting contribution from f ;

•     Break if ;

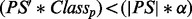•     Remove f from PS_p ;

•   } // End inner for loop.

•   Report all factors remaining in PS_p ;

• } // End outer for loop.

where (|PS|*α) is a way to adjust the number of expected false positives (FPs) and false negatives (FNs). In this study, we heavily penalized novel interactions by setting α = 0. GRA has been implemented only for PhosphoChain.

2.4 Reconstruction of the genome-wide kinome network

PhosphoChain predicted a global protein kinase–phosphates interaction (KPI) network using 162 gene DA profiles related to 144 kinase/phosphates proteins. After removing ambiguous PPIs with the GRA, we found that 37 kinase/phosphatase proteins, regulate other proteins in >15 experiments. These 37 were used to generate the KPI network shown in Figure 3. To compare coverage rates between different sets of phosphorylation events (e.g. PhosphoChain predicted interactions and interactions recorded in BioGRID), we used 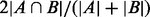as described in (Turinsky et al., 2010).

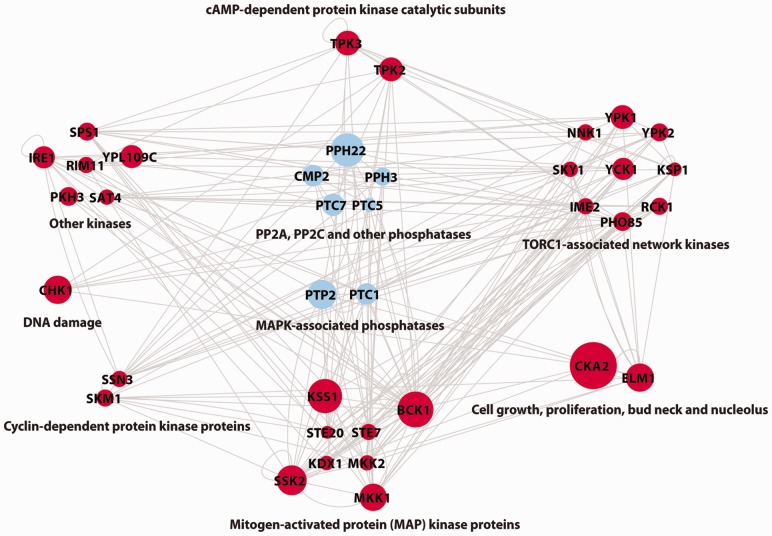
Fig. 3.

Reconstruction of the genome-wide kinome network. Shown are 37 kinases and phosphatases that were relevant in >15 experiments. Node size denotes the number of experiments under which the factor contributes to prediction scores (maximum size is 55 of 162). Arrowheads on edges are omitted to aid visual clarity. The full list of interactions (with direction) is available on the PhosphoChain web page

3 RESULTS

PhosphoChain is built on the hypothesis that proxies for PA can be used in conjunction with detection and prediction of phosphorylation motifs to reconstruct chains of phosphorylation events. PhosphoChain constructs an ADTree (Freund and Mason, 1999) that describes which kinases and phosphatases acting at specific binding sites affect the activity of a target protein. PhosphoChain generates rules based on PA measurements and the presence of putative template kinase and phosphatase binding motifs (e.g. Hog1 is activated, and a Hog1 binding motif is present) that predicts the activity level of a target protein (e.g. Ste12). PA levels are estimated from mRNA expression levels in genome-wide expression studies involving genetic perturbations. PhosphoChain works by iteratively adding good rules to a master list of rules that, together, lead to a single strong hypothesis.

PhosphoChain accepts as input a PA matrix that contains activity measurements for a set of proteins 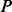across a set of experiments 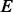(Fig. 1, panel I.1). For example, to reconstruct the MAPK pathway, P is a dataset containing 336 genes encoding KPT and E contains 28 mRNA expression experiments in which MAPK-related factors have been deleted including some experiments in which multiple genes were deleted (van Wageningen et al., 2010). Each experiment is correlated with DA measurements for the proteins when the factors 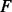(i.e. known kinases and phosphatases) are perturbed to produce an FRM. For these experiments, the DA matrix includes 6097 proteins and a dataset with perturbations of 144 kinases and phosphatases (KP). If a DA matrix is not available, then a subset of the PA matrix containing activity levels for all factors F may be used instead. However, including prior information through a DA matrix is particularly important when using mRNA expression data because it is not the ideal proxy for post-translational modification-related activity.

Similarly, PhosphoChain accepts as input protein sequences P. Figure 1, panel I.2, shows how an SASM is used to generate template (consensus) motifs 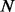that encapsulate all known target motifs 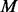present on these sequences. A Boolean MM is then generated that encodes which of the target proteins contain one or more of the 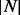motifs. PhosphoChain then generates a separate tree for each of the target proteins. As shown in Figure 1, panel I.3, the algorithm generates conditions that combine the FRM and MM to produce a CM that identifies which conditions are satisfied (e.g., factor 1 is active, and template motif 3 is present). These conditions are evaluated for each of the |E| experiments to produce the CM, which is paired with a Class vector. The Class vector represents the activity level for each target protein p during each experiment based on mRNA levels. PhosphoChain then iteratively constructs an ADTree by evaluating all |C| conditions (Fig. 1, panel II.1) and adding that rule that minimizes a weighted loss function. Thus, PhosphoChain selects the best rule for predicting p’s activity level across all experiments (Fig. 1, panel II.2). The experiments are then re-weighted so those misclassified by the previously added rule contribute more toward the subsequent rule selected in the next iteration (Fig. 1, panel II.3). After T iterations, the resulting ADTree predicts the activity level of a single protein across all conditions. Thus, each tree predicts the activity level for one protein (Fig. 1, panel III.1) and the factors and motifs that contribute to the final activity level (Fig. 1, panel III.2). This procedure is repeated for all target proteins in P, and a complete signaling network is reconstructed by chaining multiple trees together (Fig. 1, panel III.3). This is accomplished by simply ordering the predictions of each protein. The resulting network includes all predictions, thus emphasizing completeness and revealing potential complex network structure. Notably, during a given experiment, only some of the conditions may be satisfied; thus, PhosphoChain also predicts condition-specific regulation.

To test PhosphoChain’s performance and the relative importance of its components, we compared PhosphoChain to (i) PhosphoChain*, which is PhosphoChain without the DA matrix; (ii) MEDUSA, which is the inspiration for PhosphoChain and is designed to detect transcriptional regulation; and (iii) ADTree, which is essentially PhosphoChain without binding motifs. We tested these algorithms’ abilities to reconstruct the phosphorylation-related portion of the four well-studied yeast MAPK pathways shown in Figure 2 (Kanehisa and Goto, 2000) (Supplementary Table S4). PhosphoChain was trained using mRNA expression data as PA measurements for 28 gene deletion experiments (van Wageningen et al., 2010), which included deletions of genes that encode the 19 kinases and phosphatases present in the MAPK pathway. We used 10-fold cross-validation to evaluate the cutoff parameters for the FRM and MM and to compare PhosphoChain with other tools. The results demonstrate that PhosphoChain accurately predicts mRNA expression (Table 1) and that accuracy was stable for nearly all cutoffs (Supplementary Fig. S2).

Table 1.

Predicted activity of kinases, phosphatases and TFs when MAPK-related genes are deleted

Method	Recall (%)	Precision (%)	Accuracy (%)	P-value
PhosphoChain	84.39	85.22	83.87	1.40e-78
PhosphoChain*	84.99	84.52	83.59	1.36e-76
MEDUSA	86.92	83.06	83.53	4.23e-76
ADTree	73.97	62.39	62.23	—

Note: PhosphoChain* is PhosphoChain trained directly using the PA matrix without the DA matrix. Binomial P-values comparing accuracy to that for ADTree, n = 1549. No GRA (Section 2.3.2) was used here.

3.1 Reconstruction of MAPK Pathways

We then used PhosphoChain to reconstruct known MAPK pathways from experimental data. This is particularly challenging because (i) neither protein phosphorylation nor network structure data (apart from known binding motifs) were used as priors, and (ii) some factors in the pathway are known as both activators and deactivators depending on the experimental conditions, whereas other factors are known to interact, but it is not clear if one activates or deactivates the other (Supplementary Table S4).

The MAPK network as reconstructed by PhosphoChain is shown in Figure 2 (Supplementary Figs S3–S6 shows visualizations from other methods) and is scored in two different ways: (i) as a directed graph, and (ii) as an undirected graph. Table 2 shows that PhosphoChain reconstructed ∼78% of the known directed protein relationships in the MAPK pathways and ∼91% if those relationships are treated as undirected. We compared these results with MEDUSA and HeR module (Bozdag et al., 2010; Wang et al., 2012). MEDUSA is similar to PhosphoChain, but uses TF DNA binding motifs instead of kinase/phosphatase protein binding motifs. MEDUSA recapitulated ∼49% of the directed edges and ∼59% undirected. HeR module is a clustering algorithm that uses an FRM. HeR’s undirected predictions recapitulated ∼53% of the undirected edges. Because no experimental data are yet available to either substantiate or negate predictions not of the literature, it is difficult to determine whether these are false positives. If we reverse the edges revealed in the literature (Supplementary Table S4) to estimate the false positives and true negatives, then PhosphoChain has an ∼8% FPR and an ∼12% FDR for directed graphs (∼9% FPR and ∼9% FDR for undirected graphs), a better score than the those in other methods (Supplementary Tables S3 and S5). This scoring method informs the Table 2 control classifier, providing a baseline accuracy of ∼58% for the directed and 50% for the undirected graphs.

Table 2.

Performance on the reconstruction of MAPK pathway in comparison with other methods

Method	Directed graph (%)	Undirected graph (%)	P-value
PhosphoChain	77.78	91.18	4.10e-18
PhosphoChain*	56.94	67.65	1.48e-03
MEDUSA	48.61	58.82	2.77e-01
HeR Module	—	52.94	2.23e-01
ADTree	55.56	82.35	1.44e-05
Control	58.33	50.00	—

Note: PhosphoChain* is PhosphoChain trained directly using the PA matrix without the DA matrix. PhosphoChain run with only the MM predicts no MAPK interactions. PhosphoChain produces the same results regardless of whether or not the GRA algorithm (Section 2.3.2) is run.

As the available literature probably does not exhaustively list all interactions, assuming that the MAPK edges that do not appear in the literature truly do not exist would probably underestimate the classifier accuracy and be useful only for estimating an upper bound on the FDR. Regardless, if we apply this method, then we get the accuracies shown in Supplementary Table S6 where PhosphoChain generally outperforms other tested methods with a 45% FPR, a 57% FDR, a 64% accuracy and a correlation of 0.37.

To estimate PhosphoChain’s likelihood to make false-positive predictions another way, we shuffled the MAPK-related input data to mask the MAPK signal and assumed that any predictions matching known interactions are false positives. After applying this method 20 times, we estimated the FPR to be ∼3% for directed and ∼10% for undirected graphs (Supplementary Fig. S7).

3.2 Predicting phosphorylation sites

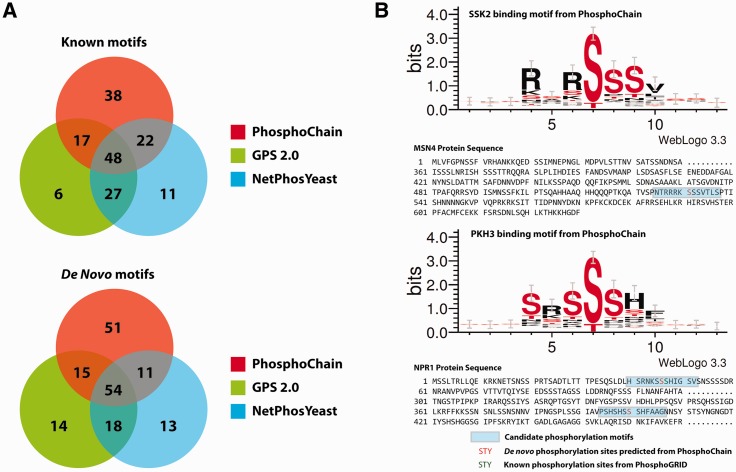
We next tested PhosphoChain’s ability to predict phosphorylation sites on a large scale using the same parameter values as in the MAPK experiments. As a reference, we used mass spectrometry mapped changes in yeast phosphorylation patterns after perturbing 97 kinases and 27 phosphatases (Bodenmiller et al., 2010). Although this dataset did not recapitulate many known phosphorylation events (e.g. in an ste7 deletion, the phosphorylation status of few known Ste7 targets changed), it did provide a good set of unique phosphorylation events. From this dataset, we selected 472 unique phosphorylation sites related to kinase, phosphatase and transcription factor proteins that had at least six residues on each side of the phosphorylation site. We trained PhosphoChain on 162 gene deletion microarray containing experiments corresponding to the 144 kinases and phosphatases (van Wageningen et al., 2010). PhosphoChain correctly identified 256 of the 472 unique phosphorylation sites present in the dataset (Fig. 4A, binomial test, P-value 3.63e-02). Strikingly, 131 of the 256 sites are phosphorylated at new motifs that were not present in the PhosphoGRID phosphorylation database (Stark et al., 2010), but were experimentally determined by Bodenmiller et al. (2010), thus demonstrating the power of PhosphoChain for discovering sites de novo (Fig. 4A). We compared these results with popular phosphorylation motif detection software packages NetPhosYeast and GPS 2.0 (Ingrell et al., 2007; Xue et al., 2008), which detected 204 and 199 of the 472 sites, respectively. Figure 4B shows two de novo motifs predicted only by PhosphoChain. Supplementary Table S7 shows motif patterns detected by PhosphoChain.

Fig. 4.

Predicting phosphorylation sites. (A) Overlap of phosphorylation binding motifs predicted by PhosphoChain, GPS2.0 and NetPhosYeast. (B) The de novo binding motif patterns for SSK2 and PHK3 proteins were detected by PhosphoChain but not by either GPS.20 or NetPhosYeast

3.3 Reconstruction of the genome-wide kinome network

We trained PhosphoChain on the 144 kinases and phosphatase deletion experiments to construct the entire KPI network shown in Supplementary Figure S8. Unfortunately, these are difficult to verify as databases of PPIs (Turinsky et al., 2010) and phosphorylation events are notoriously incomplete, generally showing poor overlap (Breitkreutz et al., 2010) even among computationally inferred networks (Bansal et al., 2007). Nevertheless, we compared the regulatory networks created by PhosphoChain with those interactions recorded in the STRING (Szklarczyk et al., 2011), BioGRID (Stark et al., 2011), KEGG (Kanehisa and Goto, 2000), YeastKinome (Breitkreutz et al., 2010), MPact (Guldener et al., 2006), MINT (Chatr-aryamontri et al., 2007) and IntAct (Kerrien et al., 2012) databases. We selected two types of interaction networks: (i) a KPT interaction network with 345 factors; and (ii) a kinase and phosphatase (KP) interaction network with 144 factors. These networks generated from PhosphoChain had a 21–29% overlap with known interactions, a better overlap than other methods tested (See Supplementary Fig. S9).

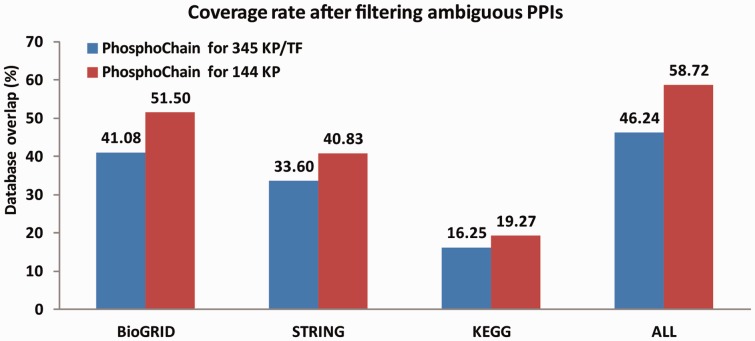
Because there is no database of KPIs that do not occur, a large number of (false positive) predictions would also yield high coverage of the known network, but give the false impression that PhosphoChain is performing well. To compensate for possible false-positive predictions, we implemented a greedy algorithm to reduce the number of predictions that PhosphoChain makes by using the following logic: If the final PA can be correctly predicted by the ADTree using only known PPIs, then we removed all other interactions from the tree. However, if the known PPIs could not account for the final PA, then we left the additional PPIs in the tree. By running this algorithm, we reduced the number of predicted interactions from 11 513 and 39 284 to 2823 and 1313 for the 345 factors and 144 factor networks, respectively. As shown in Figure 5, this increased coverage to 41%/52% with BioGRID, 34%/41% with STRING, 16%/19% with KEGG and 46%/59% overall when predicting the networks containing 345/144 factors. Overall, PhosphoChain predicted ∼52% of the KP and ∼38% of the KPT interactions as shown in Supplementary Table S8.

Fig. 5.

Analysis of interactions in PhosphoChain by overlap with interactions in previously reported datasets. The GRA was used to remove extraneous interactions. This resulted in 2823 and 1313 out of 39 384 and 10 440 maximum non-redundant interactions predicted for the 345 KPT and 144 KP datasets, respectively

Figure 3 shows 37 kinases and phosphatases [grouped by function as defined by (Breitkreutz et al., 2010)] predicted as interacting in at least 15 conditions after the GRA. These kinases and phosphatases are highly interconnected (hypergeometic test, P = 1.77e-30 compared with randomly generated networks) and thus may be key signaling hubs. This interconnectivity is consistent with a previous result that has >80% of the proteome interlinked by kinases (Breitkreutz et al., 2010).

4 CONCLUSION AND DISCUSSION

PhosphoChain predicts condition-specific phosphorylation-mediated signaling networks from high-throughput data. Specifically, it predicts the sequence of phosphorylation events, the binding sites at which phosphorylation occurs and the activity of target proteins. These predictions are based on PA measurements as approximated by mRNA expression data and consensus binding motifs generated from known phosphorylation motifs. The number of predictions is reduced using a greedy algorithm informed by known PPIs. Thus, PhosphoChain’s predicted network includes some well-established interactions and novel interactions that can be prioritized for experimental validation.

In this study, we focused on mRNA expression levels as proxies for PA. It is remarkable that mRNA can be used to predict post-translational modification status, but this is probably because signaling networks and gene regulatory networks are highly coordinated—as kinases and phosphatases become active, their gene expression levels often also increase (Avignon et al., 1995; Kusari et al., 1997; Prinz et al., 2004; Roberts et al., 2000). One possible mechanism is direct feedback. For example, in Saccharomyces cerevisiae, the TF Adr1 is activated by the kinase Snf1 (Ratnakumar and Young, 2010). Adr1-binding motifs exist in the promoter regions of both ADR1 and SNF1. (Abdulrehman et al., 2011; Chua et al., 2006). Thus, if a pathway involving Adr1 and Snf1 is activated, the expression levels of both may increase.

Regardless of the specific mechanism, the research conducted here provides strong evidence that phosphorylation and mRNA expression are linked. The ADTree presented in Tables 1 and 2 uses the FRM alone to produce an ADTree and thus is essentially PhosphoChain without the MM. In Table 1, adding the kinase/phophatase motifs to the ADTree (resulting in PhosphoChain) increases the accuracy by >20% (P < 10⁻⁷⁷). This demonstrates the effectiveness of these motifs for predicting mRNA expression, implying a link between mRNA expression phosphorylation. Table 2 uses the MAPK pathway to verify interactions predicted by PhosphoChain. The P-value for ADTree (PhosphoChain without motifs) is ∼1.44e-05, implying that mRNA data alone have information about phosphorylation. Taken together, we believe that this demonstrates that mRNA expression levels are a reasonable proxy for PA in PhosphoChain.

4.1 Extending PhosphoChain

PhosphoChain can run on other datasets by changing (i) the binding motifs, ; (ii) the DA matrix; (iii) the PA matrix; or (iv) the test data used to traverse the ADTree. The simplest way to use PhosphoChain is to traverse the network (i.e. the ADTree) using new mRNA expression data to evaluate which pathways are active. To build a new ADTree, the PA matrix would have to be changed. To run PhosphoChain on an organism other than S.cerevisiae, the DA matrix and binding motifs should be changed. As a proof-of-principle, we better reconstructed the cell wall (CW) pathway (Supplementary Fig. S10) by substituting the PA matrix and test data using 64 MAPK CW-specific experiments.

PhosphoChain also provides an extensible framework for studying other post-translational modifications and, with only relatively minor modifications, PhosphoChain could also (i) use high-throughput data other than mRNA expression; (ii) include additional biological information; and (iii) be applicable to human networks.

Because the mechanism connecting phosphorylation and mRNA expression is probably indirect, there are several other proxies for activation that might be more informative, or by inclusion could improve the predictive capabilities of PhosphoChain. These include, but are not limited to, changes in the phosphorylation status of kinases and/or phosphatases themselves and changes in protein localization, which, when combined with the motif analysis, can be used to infer temporal and causal regulation.

PhosphoChain might also be made more accurate by expanding the CM (by adding more rules or by making existing rules more complex) to accommodate the inclusion of additional biological information. Because the CM is formed using a logical conjunction of two criteria, it is conceptually simple to add additional criteria. This would be especially useful if those criteria limited the number of conditions that are true, thereby reducing the space of possible solutions. For example, kinase and phosphatase motifs conserved across species are more likely to be bona fide sites of action (Minguez et al., 2012); therefore, it should be useful to add a third criterion specifying whether or not a motif is conserved. Additionally, incorporating more information about experimental conditions (such as salt levels, pathogen exposure) could lead to models that are more predictive of network activities specific to environmental conditions.

To develop PhosphoChain, we took advantage of experimental perturbations that are most easily performed in model systems. However, the structure of PhosphoChain enables the same general approach to be applied in cases where direct perturbation data are not available as is typical for human disease networks. In these cases, genetic data, phosphoproteomic data, expression data, model organism data and so forth can all be incorporated into the same framework to predict signaling network activities.