Figure 3.

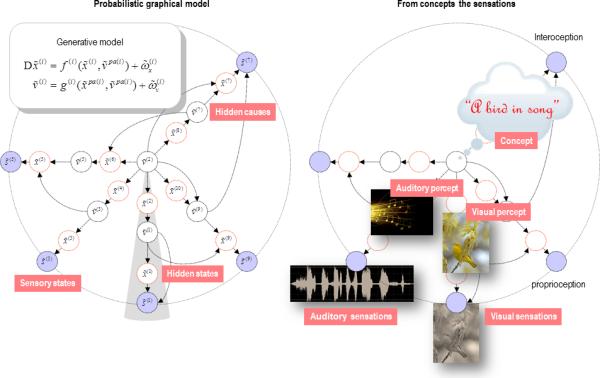
This schematic shows an example of a generative model. Generative models describe how (sensory) data are caused. In this figure, sensory states (blue circles on the periphery) are generated by hidden variables (in the centre). The left panel shows the model as a probabilistic graphical model, where unknown variables (hidden causes and states) are associated with the nodes of a dependency graph and conditional dependencies are indicated by arrows. Hidden states confer memory on the model by virtue of having dynamics, while hidden causes connect nodes. A graphical model describes the conditional dependencies among hidden variables generating data. These dependencies are typically modelled as (differential) equations with nonlinear mappings and random fluctuations ${\tilde{\omega }}^{\left(i\right)}$ with precision (inverse variance) Π⁽ⁱ⁾ (see the equations in the insert on the left). This allows one to specify the precise form of the probabilistic generative model and leads to a simple and efficient inversion scheme (predictive coding; see next figure). Here ${\tilde{v}}^{pa\left(i\right)}$ denotes the set of hidden causes that constitute the parents of sensory s̃⁽ⁱ⁾ or hidden x̃⁽ⁱ⁾ states. The ~ indicates states in generalised coordinates of motion: x̃ = (x, x′, x″,...). An intuitive version of the model is shown on the right: here, we imagine that a singing bird is the cause of sensations, which – through a cascade of dynamical hidden states – produces modality-specific consequences (e.g., the auditory object of a bird song and the visual object of a song bird). These intermediate causes are themselves (hierarchically) unpacked to generate sensory signals. The generative model therefore maps from causes (e.g., concepts) to consequences (e.g., sensations), while its inversion corresponds to mapping from sensations to concepts or representations. This inversion corresponds to perceptual synthesis – in which the generative model is used to generate predictions. Note that this inversion implicitly resolves the binding problem - by explaining multisensory cues with a single cause.