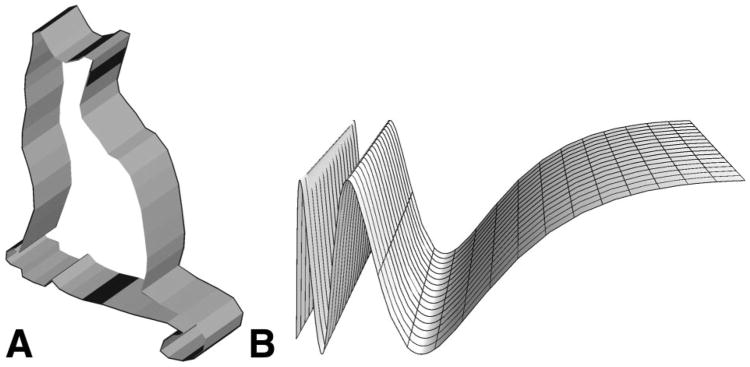
Figure 2.
Examples of 3D shapes with zero Gaussian curvature everywhere and thus—in Lim and Leek's (2012) account—constant, minimal, shape information everywhere. In both shapes, Gaussian curvature is zero everywhere because one of the two principal curvatures is zero. Under Lim and Leek's account, the cookie-cutter cat in A, unlike Attneave's (1954) cat, would have no variation in the concentration of shape information; similarly, in B, the variations in the strengths of the ridges and valleys would convey no variation in shape information. These predictions blatantly contradict intuition.