Abstract
The aims of the present study were: to identify the factors which are able to explain the performance in the 200 meters individual medley and 400 meters front crawl events in young swimmers, to model the performance in those events using non-linear mathematic methods through artificial neural networks (multi-layer perceptrons) and to assess the neural network models precision to predict the performance. A sample of 138 young swimmers (65 males and 73 females) of national level was submitted to a test battery comprising four different domains: kinanthropometric evaluation, dry land functional evaluation (strength and flexibility), swimming functional evaluation (hydrodynamics, hydrostatic and bioenergetics characteristics) and swimming technique evaluation. To establish a profile of the young swimmer non-linear combinations between preponderant variables for each gender and swim performance in the 200 meters medley and 400 meters font crawl events were developed. For this purpose a feed forward neural network was used (Multilayer Perceptron) with three neurons in a single hidden layer. The prognosis precision of the model (error lower than 0.8% between true and estimated performances) is supported by recent evidence. Therefore, we consider that the neural network tool can be a good approach in the resolution of complex problems such as performance modeling and the talent identification in swimming and, possibly, in a wide variety of sports.
Key points.
The non-linear analysis resulting from the use of feed forward neural network allowed us the development of four performance models.
The mean difference between the true and estimated results performed by each one of the four neural network models constructed was low.
The neural network tool can be a good approach in the resolution of the performance modeling as an alternative to the standard statistical models that presume well-defined distributions and independence among all inputs.
The use of neural networks for sports sciences application allowed us to create very realistic models for swimming performance prediction based on previous selected criterions that were related with the dependent variable (performance).
Key words: Evaluation, age group swimmers, individual medley, front crawl.
Introduction
Under the present conditions, talent identification represents a judgment about future performance levels based on the present individual skills and abilities. This fact brings some difficulties when it is necessary to make decisions in the present about the future talent in some specific area. The weakness of this prognosis may be conceptually due to: the contemporaneous cybernetic approach of sports sciences, where athletes are viewed as closed circuits and, thereby, an incoming training stimulus drives to an equivalent out coming response represented as an improved performance (Shestakov, 2000); difficulty to define the multi-factorial sports performance structure, due to the lack of consistent research and weak connection between the different scientific areas which support this kind of studies.
Some studies (Lees, 2002; Linder et al., 2003; Perl, 2004) tried to isolate, from a wide range of variables, those which determine mostly the success in competition. However, despite the series of assessment and types of analysis, the performance prediction is still imprecise, often pointing in different directions and making future analogy quite complex.
Several other studies based in the cybernetic model of sports performance have focused the adaptation processes as a result of different training parameters (Aminian et al., 1995; Busso et al., 1997; Herren et al., 1999; Kurz and Stergiou, 2005; Wu and Swain, 2002). In this cybernetic approach, the function of each athlete is similar to a closed circuit. Presently it is known that the robustness of this linear and simple model is not suitable to explain the dynamic system of the sportsmen behavior, which is highly influenced by the social environment, other than by the training process (Bartlett, 2006; Davids et al., 2003; Lees, 2002; Linder et al., 2003).
Based on this assumption it is necessary to change the training and adaptations concepts to a more synergetic perspective. Therefore, the interest in the versatility of non-linear methods to model sport performance arises. Presently, those non-linear methods can be used successfully in the field of complex processes as human behavior or, more specific, the human movement. Another field of application could be the sports performance analysis (Bartlett, 2006).
According to Perl, 2004, despite the different suitable applications, movements are time-dependent processes and, in this sense, they can be modeled by time - series of coordinates (e.g. each articulation has geometric coordinates). The set of the coordinates of the relevant articulations build a high-dimensional configuration. These configurations (patterns) provide reasons to analyze movement by means of neural networks (e.g. Kohonen Feature Map - KFM).
In performance analysis there are at least three methods frequently used for this purpose: Fourier analysis, Coherent State analysis and Neural Networks. Some authors have stated that artificial neural networks are a skilled and valid tool to model training process (Hahn, 2006; Liang and Liang, 2006; Shestakov, 2005).
In this context, the aims of the present study were three-fold: to identify factors which are able to explain the performance in the 200 meters individual medley (IM) and 400 meters front crawl (FC) events for young swimmers, to model the performance in those above referred events using non-linear mathematic methods by artificial neural networks (multi-layer perceptrons) and to assess the ability of neural network models to predict the swimming performance.
Methods
Subjects
A sample of 138 swimmers (65 males and 73 females) of National level was used in this study. The participants were age group swimmers and were selected to join technical and conditional evaluation. The participants provided their written informed consent and the procedures were approved by the institutional review board.
Although both boys and girls belonged to the same age group, the mean age of the males was 15.9 ± 0.4 years and the mean age of females was 13.2 ± 0.4 years. This age difference in the same age group is due to the LEN (European Swimming League) rules, which impose girls to be two years old backward comparing to boys because of an earlier biological maturation.
Evaluations
All subjects were submitted, during three days, to a test battery comprising four evaluation domains: kinanthropometric evaluation, functional evaluation (strength and flexibility), specific function evaluation (hydrodynamics, hydrostatic and bio-energetic characteristics) and semi qualitative swimming technical evaluation. In the first day, the testing included kinanthropometric and dry land functional evaluation. In the second day of testing, swimming functional and technical evaluations were performed (separated by 6- 8h).
In kinanthropometric domain, variables were selected among anthropometric measurements, body composition and somatotype. The anthropometric measures were registered according to the International Working Group on Kinanthropometry methodology described by Ross and Marfell- Jones, 1991. Body composition was assessed by bioelectrical impedance analysis (BIA 101 body fat analyzer, Akern Srl, Florence, Italy) using a four-point tactile electrodes with an alternating current of 50 kHz, 500 μA, after a overnight fast. The somatotype was determined according to the Heath and Carter (1966; 1967) technique. A total of six skin folds were taken with a skin fold caliper Slim Guide (Creative Health products, EUA). Endomorphism, mesomorphism and ectomorphism components were calculated by the equations proposed by Ross and Marfell-Jones, 1991. To evaluate body dimensions a stadiometer with a range scale of 0.10 cm was used and body weight was measured to the nearest 0.1 kg using a digital scale (Weight Tronix, New York, USA). The variables assessed in the kinanthropometric domain were: body dimensions (weight, height, span and sitting height), body longitudes (length and width of the hand, length and width of the foot, length of superior and inferior limbs), diameters: biiliocrista (hip width), bideltoid (shoulder width) and toroco-sagital (chest depth), body indexes (span/height and body mass index), body composition: fat-free mass and Somatotype (endomorphism, mesomorphism and ectomorphism).
In dry land functional evaluation, strength and flexibility tests were made (Carzola, 1993; Costill et al., 1992). For strength tests, abdominal muscular endurance (maximum repetitions in 60 seconds), back lumbar muscular endurance (maximum repetitions in 60 seconds), vertical impulse strength, Squat Jump (Ergo Jump, Bosco System, Globus, Italy), Handgrip strength (Jackson Evaluation dynamometer System, Texas Instruments, USA) and average isometric strength of upper limbs (Jackson Evaluation dynamometer System, Texas Instruments, USA) were implemented. For flexibility, the following measures were taken (Carzola, 1993; Costill et al., 1992) with a Gollehon extendable goniometer (Lafayette Instrument Co, USA): flexion and extension of the ankle, flexion and extension of the shoulder and flexion and extension of the trunk.
The swimming functional evaluation domain comprised three different categories registered as follow: hydrodynamic characteristics measured by the maximum distance achieved by the swimmer in ventral gliding, after a push off in the wall (Carzola, 1993; Costill et al., 1992), hydrostatic characteristics measured by vertical and horizontal buoyancy (Carzola, 1993) and bioenergetics characteristics assessed by the swim velocity at lactic threshold (LT) and maximum value of accumulated blood lactate. Lactate measurements were performed according to the procedure developed by Mader et al., 1976. The swimmers performed 2x200m front crawl, at 80% and at 100% of their maximum speed (according to their best time at 200m front crawl), with a 30 minutes recovery between bouts. One, three and five minutes after each bout blood samples were collected from the ear lob. Blood lactate was measured with an Accusport analyzer (Boheringer, Mannheim, Germany). Lactic threshold was considered to be corresponding to a blood lactate concentration of 4 mmol·l-1 and it was determined by linear interpolation of the points relating blood lactate and swimming speed.
Semi qualitative swimming technical evaluation was performed in order to evaluate technical efficiency. The detected errors were registered in a criterion observation check list. Each swimmer performed a maximal 4x25 m trial test in each one of the swimming techniques: butterfly, backstroke, breaststroke, front crawl. Recovery between trials was 30 min and the order of the swimming styles was randomly assigned. Each trial was videotaped both underwater and above the water in the sagital plane with JVC- SVHS synchronized cameras. Both images were mixed using a Panasonic WJMX50 mixing table. In order to obtain a dual media final image, the optical axis of each video camera was parallel between each other. Both video cameras provided images on the sagital plane since they were placed in the lateral wall of the pool, 30 cm underwater and 30 cm over the water surface. The cameras were placed at 7.5 m distance with the optical axis perpendicular to the swimmers plane of displacement. A third underwater fixed camera was placed in frontal plane, with the optical axis perpendicular to the optical axis of the others two cameras at 5 m distance. The third camera image was synchronized with the sagital cameras images using a traditional synchronized focus system, visible in the visual camp of each located camera (Vilas-Boas, 1996). A semi-qualitative swimming technical evaluation was made on the images that were recorded using an observation system (Chollet, 1990; Costill et al., 1992; Maglischo, 2003). Each observation was quantified based on relative criteria of technical faults (Reischle, 1993), where different points represent the swimming effectiveness. The variables measured for each one of the swimming techniques were subdivided in four main criterions: body balance, arm action, leg action and movement synchronization.
Performance
The best performance in 400 meters FC and 200 meters IM were used as dependent variables. The best time recorded in each event closest to the evaluation moment was considered. Those times were converted into points according to the “International Point Score System” (IPS) (www.swimnews.com, Canada). This system was used and validated for any kind of competition as demonstrated in the punctuation system of FINA 2003' World Cup Series. The system distinguishes values for each performance in a scale that varies from 0 to 1100 points, corresponding to world class performances.
Table 1 present average scores of performance in both events considered in this work.
Table 1.
verage scores of the subject's performance in 400 meter FC and 200 meter IM. Data are means (±SD).
| 400 meters FC | 200 meters IM | |||
|---|---|---|---|---|
| Average time (min:sec) |
IPS | Average time (min:sec) |
IPS | |
| Males (n = 65) | 4:29.56 (0:24.12) | 680 (54) | 2:24.45 (0:12.21) | 658 (60) |
| Females (n = 73) | 5:02.95 (0:35.37) | 652 (73) | 2:46.09 (0:19.92) | 613 (75) |
Data analysis
Mean and standard deviation (SD) were calculated for all variables. The Kolmogorov-Smirnov test of normality and Levine's test of homogeneity of variance were performed to verify the normality of the distribution. Pearson product-moment correlation coefficient or Spearman correlation coefficient were used, whenever appropriate, to verify the association between variables. Data was analyzed using SPSS 10.1 (Chicago, IL). The significance threshold was set at p < 0.05.
Considering internal validity (intra and inter observer validity) of semi qualitative technical evaluation, a randomize selection of 75% swimmers were re-evaluated. Each one of these swimmers was evaluated two times by the same observer and a third time by another expert. The first two evaluation moments (same observer) were undertaken with one month interval. The third evaluation period (different observer) was made at the same time of the second moment (first observer). After the semi qualitative technical evaluation, the intra and inter observer agreement were performed, using the Kappa Cohen Index for ordinal variables and the R of Spearman correlation coefficient for ratio variables.
The performance modeling was accomplished by a feed forward neural network with three neurons in a single hidden layer, as shown in Figure 1.
Figure 1.
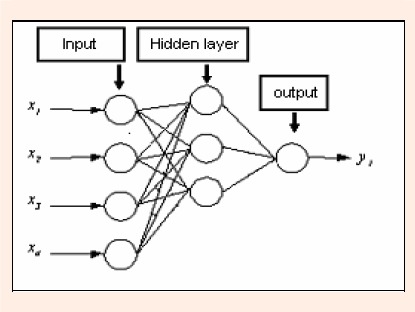
Feed forward neural network with one hidden layer.
Hornik et al. (1989) demonstrated that this Multilayer perceptron (MLP) net type with one hidden layer is a universal approach element. Though, it may be used to approach any typical function f, with acceptable accuracy trough the follow expression:
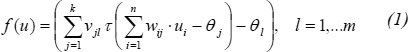 |
Where: τ is the activation function, k is the number of hidden unities, vjl and wij represent weights, Өi are polarization values (biases) and u is the data vector.
The non-linear function f was estimated using the optimization method of Lavenberg-Marquardt which is a standard method to minimize the mean square error, due to its properties of convergence and robustness (Marquardt, 1963).
The weight initialization was performed with the decline method of Nguyen and Widrow (1990). This method was used in way to force its magnitude to lower levels through an addition of a regulation term into the expression of the mean square error (Principe et al., 2002). Normalization of data was performed with standard techniques.
The neural network training and performance was done using the following objective function:
Where: N is the number of data samples considered, ỳ represents the true output by the neural network and represents the estimated output by the neural network.
Eighty percent of each dataset was randomly used to estimate the model and the remaining 20% was used to validate it. The training stopped when the compromise between the performance in minimization of the training set error and the quality of the obtained generalization of the validation set were satisfactory. In the test developed, it was verified that 600 seasons were sufficient for this application.
Four predictive models were built for each gender and dependent variable (400 meters FC and 200 meters IM) including variables with significant correlations (input). It was considered the eventuality of getting redundant functions due to the large number of variables (Streiner and Norman, 2006), still guarding against the non integration of interrelated variables.
Results
Regarding the analysis of internal validity of semi qualitative swimming technical evaluation, 75% of the ratio variables that were studied (96) presented correlation coefficients (inter and intra observer) of r = 1 (p = 0.000). In the other variables (32) high correlation coefficients were also found (r = 0. 884, p = 0.047). As for the ordinal variables, the Kappa Cohen Index values were always equal to 1, thus representing a perfect agreement between the absolute evaluations that were made.
Bi- varied Correlations
Tables 2 and 3 present the bi-varied correlations observed in male and female subjects, respectively.
Table 2.
Mean and standard deviation (SD) of the variables that correlated with the performance over 200m IM or over 400m FC in male swimmers. Correlation coefficients (r) are also shown.
| Domain | Variables | Mean (±SD) | r (400m FC performance) | r (200m IM performance) |
|---|---|---|---|---|
| Anthropometry | ||||
| Height (cm) | 172.20 (6.63) | (r = .305 p<.05) | (r = .365 p<.05) | |
| Span/height index (cm) | 1.06 (.04) | (r = -.335 p<.05) | (r = -.357 p<.05) | |
| Chest Depth diameter | 20.81 (1.74) | – | (r = .553 p<.01) | |
| Fat-free mass (%) | 84.2 (3.5) | (r = .315. p<.05) | – | |
| Fat mass (%) | 15.8 (3.5) | (r = .310. p<.05) | – | |
| General F. (flexibility) | ||||
| Ankle flexion (°) | 105.53 (51.98) | – | (r = -.730 p<.01) | |
| Trunk extension (cm) | 29.74 (7.55) | – | (r = -.553 p<.05) | |
| Specific Functional | ||||
| LT swim velocity (4 mmol·l-1) (m·s-1) | 1.40 (.08) | (r = .756. p<.01) | (r = .656 p<.01) | |
| Glide (cm) | 6.67 (.73) | (r = .807. p<.01) | – | |
| Technical effectiveness | ||||
| Crawl technique - arm exit (%) | 84.9 (36.4) | (r = .461. p<.05) | (r = -.465 p<.05) | |
| Breaststroke technique - leg down sweep (%) | 47.0 (35.2) | – | (r = -.546 p<.01) | |
Neural network models
Only the independent variables that were significantly associated with performance (400 meters FC and 200 meters IM) were included in this application. In table 4, the differences between the true performance values (IPS, swim news, Canada) and estimated performance values based on the application of neural network models are presented.
Table 4.
Mean of the differences between the true performance values and estimated values for each one of the events evaluated, based on the application of neural network models. Data are means (±SD).
| 200 IM | 400m FC | Total | ||||
|---|---|---|---|---|---|---|
| Male | Female | Male | Female | Male | Female | |
| Points (IPS) | 5.7 (49.2) | ˗3.0 (42.8) | 4.8 (26.8) | 3.3 (49.1) | 4.5 (39.6) | .2 (46.0) |
| % | 1.7 (13.3) | ˗.2 (6.9) | .6 (4.3) | .7 (7.8) | 1.2 (9.8) | .2 (7.3) |
Modeling of the 400 meters FC performance
The modeling of the 400 meters FC event in male swimmers involved the integration of height, span/height index, fat-free mass, fat mass, swim velocity at lactic threshold, glide and technical effectiveness in the arm exit phase in FC. In female swimmers, the modeling of the 400 meters FC event involved the integration of leg length, swim velocity at lactic threshold, technical effectiveness in FC (arms/global), technical effectiveness in arms down sweep phase and arm exit phase in FC.
The estimated model in males predicted an average score of 675.2 ± 52.4 (4min 30.60sec ± 11.70sec), while the true average score was of 680 ± 54.0 (4min 29. 56sec ± 24.12sec). An average difference of 4.8 ± 26.8 points was verified, which represents an estimation error of prediction of approximately 0.6 ± 4.3%. In female swimmers the model predicted an average score of 649.0 ± 66.0 (5min 03.55sec ± 15.66sec), which confronts with a true average of 652.3 ± 72.8 (5min 02.95sec ± 35.37sec). An average difference of 3.3 ± 49.1 points was verified, which represents an estimation error of prediction of approximately 0.7 ± 7.8%.
Modeling of the 200 meters IM performance
The modeling of the 200 meters IM event for male swimmers involved the integration of height, span/height index, chest depth diameter, ankle flexion, trunk extension, swim velocity at lactic threshold, technical effectiveness in breaststroke (leg down sweep) and in FC (arm exit). In female swimmers, the modeling of this event involved the integration of height, leg length, foot length, depth chest diameter, hand press strength, swim velocity at lactic threshold, maximum lactate accumulation, technical effectiveness in backstroke (legs), FC (global), FC (arms global), FC (arm exit).
The estimated model in male swimmers predicted an average score of 652.7 ± 72.7 (2min 25. 03sec ± 16.15sec), while the true average score was of 658.4 ± 59.9 (2min 24.45sec ± 12.21sec). An average difference of 5.7 ± 49.2 points was observed, which represents a mean variation between true and estimated performance of just 1.7 ± 13.3%.
For female swimmers the result of the constituted model predicted an average score of 615.8 ± 76.4 (2min 45.75sec ± 20.56sec), which confronts with true average of 612.8 ± 74.9 (2min 46.09sec ± 19.92sec). The average value of the difference between true and estimated performance was of -3.0 ± 42.8 points, which represents an estimation error of prediction of approximately -0.2 ± 6.9%.
Discussion
Bi varied correlations
Several authors (Lees, 2002; Linder et al., 2003; Geladas et al., 2005; Perl, 2004) have been trying to isolate, from a wide range of variables, those which determine mostly the success in competition. However, despite the series of assessment and types of analysis, the prediction of the performance is still imprecise (Geladas et al., 2005).
In male swimmers, height correlated positively with the performance in both events, which supports previous findings (Lees, 2002; Linder et al., 2003; Mazza et al., 1993). In the present study, some body composition variables (fat-free mass and fat mass) were correlated with performance in 400 meter FC. Depth chest also correlated with the performance in 200 meter IM event.
In female swimmers, the performance in the 200 meter IM event correlated with chest depth, foot length and with height and confirms the results obtained previously by Kubiak-Janczaruk (2005).
According to our results, strength did not seem to determine performance in age group swimmers, at least in the general parameters that were evaluated. Our results showed only a single significant association between strength measures and performance. This lack of significant associations is at odds with previous studies with swimmers (Smith et al., 2002). The lack of associations between strength and swimming performance may be due to: the fact that the association between strength and performance becomes more evident at high swimming velocities, namely in shorter duration events than those that we have used (Christensen and Smith, 1987; Costill et al., 1980; 1983; Geladas et al., 2005; Hawley et al., 1992; Klentrou and Montpetit, 1991; Roberts et al., 1991; Toussaint and Vervoorn, 1990); the fact that there is a tenuous transfer of dry land strength to swimming, especially when the load and movement velocity is held constant (Olbrecht et al., 1985; Sharp et al., 1982). Watanabe and Takai, 2005 tried to analyze the factors that contribute to swimming performance and to determine the extent to which these factors change with respect to age group swimmers' development. Their results suggest that muscle strength does not contribute strongly to the swimming performance in subjects who are less than 14-years-old. Contrarily, they concluded that muscle strength was an important explanatory factor of swimming performance in 50 m FC in swimmers of both genders over 15-years-old.
We have found some significant correlations with the 200 meters IM performance and flexibility measures in males, such as foot plantar flexion and trunk extension. Although the association values were weak, these results agree with the data presented in the literature. The study of Saavedra, 2002 presents a significant correlation with trunk flexion (r = 0.294, p < 0.05). Rama and Alves, 2004 confirmed this association (r = 0.207, p < 0.19) and found also an association with the shoulder flexion (r = 0.272, p < 0.37). The absence of significant associations in the females is confirmed by the results of the abovementioned studies. On the other hand, the study of Geladas et al., 2005 presents significant associations between shoulder flexibility and performance in 100 m FC in both genders. However, the degree of association was considerably lower in girls, compared with boys.
The magnitude of the correlations between swimming velocity at LT and both performance variables corroborates the findings by others (Kubiak-Janczaruk, 2005; Smith et al., 2002). However, those studies did not follow the same methodology used in the present study to assess the performance.
The maximum lactate accumulation may indicate anaerobic energy release and this variable is seldom associated with the performance in shorter swimming distances (Bonifazi et al., 1993). Our observations are consistent with this assumption in female swimmers, since we have found associations of that variable with the performance in the 200 meters event but not with the 400 meters performance. However, in males, no association was found between maximum lactate accumulation and performance. Although that there is an early development of anaerobic power in female swimmers, the absence of association in males may not be explained by such phenomenon, since the boys were two years older than girls. In our sample, the maximum lactate accumulation does not seem to be a determinant parameter in the males 200 meters IM performance.
Concerning the hydrodynamic skill glide in males, we found a significant association with the 400 meters FC event, matching the results of Rama and Alves, 2004 (r = 0.372, p < 0.01) and of Saavedra, 2002 (r = 0.528, p < 0.01). In females we did not find significant associations, therefore confirming the results presented by Rama and Alves, 2004 (r = 0.425, p < 0.01).
In our sample, buoyancy did not correlate with the performance (in both genders), thus confirming the results of Rama and Alves, 2004. Saavedra, 2002 observed a significant association between vertical buoyancy and swimming performance in females (r = -0.357, p < 0.01). This disagreement may be due to the differences on body composition between subjects of the different studies (Dobein and Holmer, 1974).
The associations between semi-qualitative technical parameters and performance in the present study are limited to few significant correlations observed in crawl stroke in females. These results converge with Saavedra, 2002, which suggests the non relevance of technical skills for performance in these ages.
Neural network models
The non-linear analysis resulting from the use of feed forward neural network allowed the development of four performance-prediction models.
Figures 2 and 3 illustrate the comparisons between true and estimated performance values (males and females) in 400 meters FC and 200 meters IM, respectively. The yy axis represents the true and estimated scores in the events, shown as punctuation system; xx axis represents each one of the analyzed cases. The white boxes represent the neural network prediction and the black circles represent the true value.
Figure 2.
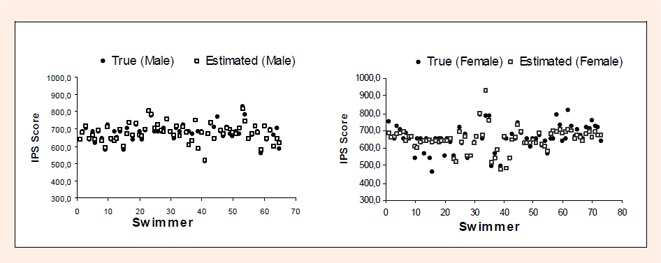
Model estimation to the 400 meters FC event for male (left) and female (right) swimmers.
Figure 3.
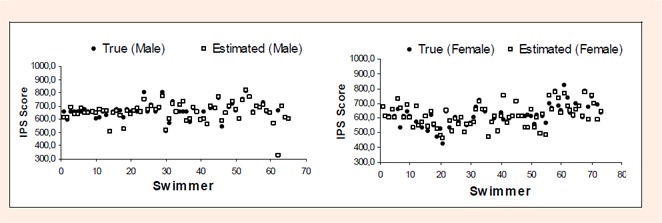
Model estimation to the 200 meters IM event for male (left) and female (right).
As we can observe in Table 4, the mean difference between the true and estimated results performed by each one of the four neural network models constructed was low, fact that is in accordance with the results presented by others that have used the same approach (Hahn, 2006; Lees, 2002; Liang and Liang, 2006; Linder et al., 2003). In the study of Hohmann et al., 2001 the neural network was able to model the swimming performance in 19 competitions with a mean estimation error of 0.62 to 0.61 sec. It was also possible to predict the semi final time for 200 m backstroke event in Sydney 2002, based on the data of two previous specific training phases with a mean error of ± 0.04 sec. In a similar study, Lees, 2002 applied the neural network method to predict the swimming performance in competition based on some criteria of talent identification. The performance estimated results were predicted for three different moments: six months, 18 months and 30 months. The deviations between the estimated performance and the true time were ≈4.64 sec in the first evaluation moment (six months), ≈3.16 sec in the second evaluation moment (18 months) and ≈3.03 sec in the final evaluation moment (30 months).
In recent years, concepts and tools from dynamical systems theory have been successfully applied to the study of movement systems, contradicting traditional views of variability as noise or error. In this perspective, it is apparent that variability in movement systems is omnipresent and unavoidable due to the distinct constraints that shape each individual's behaviour (Davids et al., 2003). In our opinion the neural network tool can be a useful approach in the resolution of performance modeling problems. Standard statistical models such as logistic regression and multivariate analysis assume well-defined distributions (e.g. normal distribution). On the other hand, they also assume independence among all inputs and are limited to linear relationships. However, these requirements rarely are met in real life systems. As an alternative to these models artificial neural networks can be used (Linder et al., 2003; Davids et al., 2003). Therefore, in this paper it was tried to illustrate the significant improvements of neural networks performance and robustness for non-linear signal predictions.
This technique may also be extended to performance analysis in other sports. Indeed, Maier et al., 2000 attempted to model the movement pattern of the shot put event. For that purpose, those authors developed a neural network model able to predict the maximum flight distance based on the technical data applied. The estimation error between the distance of the ball predicted by the model and the true distance was only 2.5%. On the other hand, trends for studying coordination and control have shifted from simple movement models toward complex, multi-joint actions in sports such as cricket (Davids et al., 2005). The use of such movement models exemplifies the nature of interacting constraints that shape emergence of coordination and control processes as proposed by dynamical systems theory and ecological psychology.
Conclusion
The use of neural network technology in sports sciences allowed us to create high realistic models of swimming-performance prediction based on previous selected criterions that were related with the dependent variable (performance). The accuracy of the predictive models that were developed supports previous data from the literature. Therefore, it was considered that the neural network tool can be a good approach in the resolution of complex problems, such as performance modeling and the talent identification in a wide variety of sports and, specifically, in swimming.
Table 3.
Mean and standard deviation (SD) of the variables that correlated with the performance over 200m IM or over 400m FC in female swimmers. Correlation coefficients (r) are also shown.
| Domain | Variables | Mean (±SD) | r (400m FC performance) | r (200m IM performance) |
|---|---|---|---|---|
| Anthropometry | ||||
| Height (cm) | 158.86 (4.93) | – | (r = .315 p<.05) | |
| Leg length (cm) | 86.76 (9.41) | (r = -.304 p<.05) | (r = -.356 p<.01) | |
| Foot length (cm) | 23.79 (1.11) | – | (r = .336 p<0.01) | |
| Chest Depth diameter (cm) | 18.11 (1.58) | – | (r = .715 p< .01) | |
| General F. (strength) | ||||
| Hand press (N) | 25.79 (3.93) | – | (r = .699. p<.01) | |
| Specific Functional | ||||
| LT swim velocity (4 mmol·l-1) (m·s-1) | 1.28 (.07) | (r = .832 p<.01) | (r = .764. p<.01) | |
| Maximum lactate accumulation (mmol·l-1) | 6.53 (1.21) | – | (r = .588. p<.01) | |
| Technical effectiveness | ||||
| Backstroke tech. - legs (%) | 89.1 (21.9) | – | (r = .588. p<.01) | |
| Crawl tech. - global (%) | 60.0 (16.3) | – | (r = .414. p<.05) | |
| Crawl tech. - arms/global (%) | 45.8 (21.0) | – | (r = .399. p<.05) | |
| Crawl tech. - arms/down sweep (%) | 35.2 (30.4) | (r = .510 p<.05) | (r = .435. p<.05) | |
| Crawl tech. - arms/exit (%) | 78.1 (42.0) | (r = .400 p<.05) | – | |
Biographies

António José Silva
Employment
Associate Professor at the Sport Sciences Department of the University of Trás-os-Montes and Alto Douro,UTAD, Portugal.
Degree
PhD.
Research interests
Physiological and biomechanical indicators of energy cost during physical activities, namely in swimming.
E-mail: ajsilva@utad.pt

Aldo Manuel Costa
Employment
PhD student of the University of Trás-os-Montes and Alto Douro,UTAD, Portugal.
Degree
MD.
Research interests
The application of neural network technology to model sports performance
E-mail: mcosta.aldo@gmail.com

Paulo Moura Oliveira
Employment
Assistant Professor of the Engineering Department Systems at the University of Trás-os-Montes and Alto douro (UTAD), Portugal.
Degree
MS, PhD.
Research interests
Computational Intelligence applications to automation and control
E-mail: oliveira@utad.pt

Victor Machado Reis
Employment
Assistant Professor at the Sport Sciences Department of the University of Trás-os-Montes and Alto Douro,UTAD, Portugal.
Degree
PhD.
Research interests
Physiological and biomechanical indicators of energy cost during physical activities
E-mail: vreis@utad.pt

José Saavedra
Employment
Associate Professor of the Faculty of Sports Science of the University of Extremadura, Spain.
Degree
PhD.
Research interests
The physiological and biomechanical analysis of swimming performance
E-mail: jsaavdra@unex.es

Jurgen Perl
Employment
Full Professor of the Institute of Computer Science of the University of Maiz, Germany.
Degree
PhD.
Research interests
Modelling and simulation, software technology and computer science in sport
E-mail: perl@informatik.uni-mainz.de

Abel Rouboa
Employment
Associate Professor at the Engineering Department of the University of Trás-os-Montes and Alto Douro (UTAD), Portugal.
Degree
PhD.
Research interests
Computational fluid dynamics, biomechanics
E-mail: rouboa@utad.pt

Daniel Almeida Marinho
Employment
PhD student of the University of Trás-os-Montes and Alto Douro, UTAD, Portugal.
Degree
MS.
Research interests
The biomechanical and physiological determinant factors of the sports performance, specially the swimming performance.
E-mail: dmarinho@utad.pt
References
- Aminian K, Robert P, Jequier E, Schutz Y. (1995) Incline, speed, and distance assessment during unconstrained walking. Medicine and Science in Sports Exercise 27, 226-234 [PubMed] [Google Scholar]
- Bartlett R. (2006) Artificial intelligence in sports biomechanics: New dawn or false hope? Journal of Sports Science and Medicine (online) 5, 474-479 Available from URL: http://www.jssm.org [PMC free article] [PubMed] [Google Scholar]
- Busso T, Denis C, Bonnefroy R, Geyssant A, Lacour J. (1997) Modeling of adaptations to the physical training by using a re-cursive least squares algorithm. Journal of Applied Physiology: Respiratory, Environmental and Exercise Physiology 82, 1685-1693 [DOI] [PubMed] [Google Scholar]
- Bonifazi M, Martelli G, Marugo L, Sardella F, Carli G. (1993) Blood lactate accumulation in top level swimmers following competition. Journal of Sports Medicine Physical Fitness 33, 13-18 [PubMed] [Google Scholar]
- Christensen C., Smith G. (1987) Relationship of maximum sprint speed and maximal stroking force in swimming. Journal of Swimming Research 3(2), 18-20 [Google Scholar]
- Carzola G. (1993) Specific tests to the swimmer evaluation. Cestas, Association pour la recherche et l'evaluation en activité physi-que et en sport. EditionsVigot, Paris. (In French) [Google Scholar]
- Chollet D. (1990) Scientific approach of the sportive swimming. Edi-tionsVigot, Paris. (In French) [Google Scholar]
- Costill D, Sharp R, Troup J. (1980) Muscle strength: Contribu-tions to sprint swimming. Swimming World 21, 29-34 [Google Scholar]
- Costill D, King D, Holdren A, Hargreaves M. (1983) Sprint speed vs. swimming power. Swimming Technique 1983, 20-22 [Google Scholar]
- Costill D., Maglischo E., Richardson A. (1992) Swimming. Hand-book of Sports Medicine and Science. Blackwell Scientific Publications, Oxford [Google Scholar]
- Davids K, Araujo D, Glazier P, Bartlett R.M. (2003) Movement systems as dynamical systems: the role of functional variability and its implications for sports medicine. Sports Medicine 33, 245-260 [DOI] [PubMed] [Google Scholar]
- Davids K, Renshaw I, Glazier P. (2005) Movement models from sports reveal fundamental insights into coordination processes. Exercise and Sport Science Reviews 33, 36-42 [PubMed] [Google Scholar]
- Dobein W, Holmer I. (1974) Body composition, sinking force and oxygen uptake in competitive swimming style. European Jour-nal of Applied Physiology 33, 105-118 [Google Scholar]
- Geladas N.D., Nassis G.P., Pavlicevic S. (2005) Somatic and physical traits affecting sprint swimming performance in young swimmers. International Journal of Sports Medicine 26(2), 139-144 [DOI] [PubMed] [Google Scholar]
- Hahn M.E. (2006) Feasibility of estimating isokinetic knee torque using a neural network model. Journal of Biomechanics, in press [DOI] [PubMed] [Google Scholar]
- Hawley J.A., Williams M.M., Vickovic M.M., Handcock P. J. (1992) Muscle power predicts freestyle swimming performance. British Journal of Sports Medicine 26, 151-155 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heath B.H., Carter J. E. (1966) A comparison of somatotype meth-ods. American Journal of Physical Anthropology 24, 87-99 [DOI] [PubMed] [Google Scholar]
- Heath B.H., Carter J.E. (1967) A modified somatotype method. American Journal of Physical Anthropology 27(1), 57-74 [DOI] [PubMed] [Google Scholar]
- Herren R, Sparti A, Aminian K, Schutz Y. (1999) The prediction of speed and incline in outdoor running in humans using accel-erometry. Medicine and Science in Sports Exercise 31, 1053-1059 [DOI] [PubMed] [Google Scholar]
- Hohmann A., Edelmann-Nusses J., Hennerberg B. (2001) Modeling and prognosis of competitive performance in elite swimming. XIX International Symposium on Biomechanics in Sports, June 20-27, San Francisco, USA. Proceedings. 54-57 [Google Scholar]
- Hornik K., Stinchcombe M., White H. (1989) Multi-layer feed forward networks are universal aproximators. Neural Networks 2, 359-366 [Google Scholar]
- Klentrou P.P., Montpetit R.R. (1991) Physiological and physical correlates of swimming performance. Journal of Swimming Re-search 7(1), 13-18 [Google Scholar]
- Kubiak-Janczaruk E. (2005) Spirometric evaluation of the respiratory system in adolescent swimmers. Annales Academiae Medicae Stetinensis 51(2), 105-113 [PubMed] [Google Scholar]
- Kurz M.J., Stergiou N. (2005) An artificial neural network that utilizes hip joint actuations to control bifurcations and chaos in a passive dynamic bipedal walking model. Biological Cybernet-ics 93(3), 213-221 [DOI] [PubMed] [Google Scholar]
- Lees A. (2002) Technique analysis in sports: a critical review. Journal of Sports Science 20, 813-828 [DOI] [PubMed] [Google Scholar]
- Linder R., Mohamed E. I., De Lorenzo A., Poppl S. J. (2003) The capabilities of artificial neural networks in body composition re-search. Acta Diabetol 40(Suppl 1), S9-14 [DOI] [PubMed] [Google Scholar]
- Liang Y, Liang X. (2006) Improving signal prediction performance of neural networks through multiresolution learning approach. IEEE Transactions on Systems, Man, and Cybernetics 36, 341-352 [DOI] [PubMed] [Google Scholar]
- Mader A., Liesen H., Heck H., Phillipi H., Rust R., Scharch P., Hullmann W. (1976) Specific tests to evaluate physical condi-tion in sports. Sports Medicine and Art 27, 80-112 (In German: English abstract; ). [Google Scholar]
- Maier K. D., Maier P., Wagner H., Blickhan R. (2000) Neural network modelling in sport biomechanics based on the example of shot-put flight. XVIII International Symposium on Biome-chanics in Sports, June 25-30, Hong Kong. Proceedings. 26-29 [Google Scholar]
- Maglischo E.W. (2003) Swimming fastest. Mayfield Publishing Company, California [Google Scholar]
- Marquardt D. (1963) An algorithm for least-squares estimation of nonlinear parameters. SIAM Journal on Applied Mathematics 11, 164-168 [Google Scholar]
- Mazza J., Ackland T., Bach T., Cosolito P. (1993) Absolute body size. In: Kinantropometry in aquatic sports: A study of world class athletes. Eds: Carter L., Ackland T.Champaign, Illinois: Human Kinetics Books; 15-54 [Google Scholar]
- Nguyen D., Widrow B. (1990) Improving the learning speed of a 2-layer neural network by choosing initial values of the adaptive weights. International Joint Conference on Neural Networks, June 17-21, San Diego, USA. Proceedings III. 2063-2068 [Google Scholar]
- Olbrecht J., Madsen O., Mader A., Liesen H., Hollmann W. (1985) Relationship between swimming velocity and lactic con-centration during continuous and intermittent training exercises. International Journal of Sports Medicine 6(2), 74-77 [DOI] [PubMed] [Google Scholar]
- Perl J. (2004) A neural network approach to movement pattern analysis. Human Movement Science 23, 605-620 [DOI] [PubMed] [Google Scholar]
- Principe J, Euliano N, Garani S. (2002) Principles and networks for self-organization in space-time. Neural Network 15, 1069-1083 [DOI] [PubMed] [Google Scholar]
- Rama L., Alves F. (2004) Determinant factors of the youth Portu-guese swimmers. 27th Scientific Congress of the Portuguese Swimming Coaches Association, May 1-2, Lisbon, Portugal. Book of Abstracts. 24-26. (In Portuguese: English abstract; ). [Google Scholar]
- Reischle K. (1993) Biomechanics of swimming. Editorial Gymnos, Madrid. (In Spanish) [Google Scholar]
- Roberts A.J., Termin B., Reilly M.F., Pendergast D.R. (1991) Effectiveness of biokinetic training on swimming performance in collegiate swimmers. Journal of Swimming Research 7(3), 5-11 [Google Scholar]
- Ross W.D., Marfell-Jones M.J. (1991) Kinanthropometry. In: Physiological testing of the high-performance athlete. Eds: MacDougall D., Wenger H., Green H.Champaign, Illinois: Human Kinetics Books; 22-29 [Google Scholar]
- Saavedra J.M. (2002) Multidimensional measurements and perform-ance in youth swimmers of national level. Doctoral thesis, University of Coruña, Coruña. 1-134 (In Spanish: English abstract; ). [Google Scholar]
- Sharp R, Troup J, Costill D. (1982) Relationship between power and sprint freestyle swimming. Medicine and Science in Sports and Exercise 14, 53-56 [DOI] [PubMed] [Google Scholar]
- Shestakov M.P. (2000) Artificial intelligence in sport science of the 21st century. Theory and Practice of Physical Education 7, 8-14 (In Russian: English abstract). [Google Scholar]
- Shestakov M. P. (2005) Modeling of technical training of discus throw-ers in the period of significant changes of their mass-inertia characteristics. Journal of Physiological Anthropology and Ap-plied Human Science 24, 367-370 [DOI] [PubMed] [Google Scholar]
- Smith D. J., Norris S.R., Hogg J.M. (2002) Performance evaluation of swimmers: scientific tools. Sports Medicine 32, 539-554 [DOI] [PubMed] [Google Scholar]
- Streiner D.L., Norman G.R. (2006) "Precision" and "accuracy": Two terms that are neither. Journal of Clinical Epidemiology 59, 327-330 [DOI] [PubMed] [Google Scholar]
- Toussaint H, Vervoorn K. (1990) Effects of specific high resis-tance training in the water on competitive swimmers. International Journal of Sports Medicine 11, 228-233 [DOI] [PubMed] [Google Scholar]
- Vilas-Boas J.P., Cunha P., Figueiras T., Ferreira M., Duarte J.A. (1996) Movement analysis in simultaneous swimming techniques. In: Symposium of Sportive Swimming. Eds: Wilke K., Daniel K., Hoffmann U., Klauck J.Bochenem: Sport Fahnemann Verlag; 95-103 [Google Scholar]
- Watanabe M, Takai S. (2005) Age-related change of the factors affecting swimming performance in junior swimmers. Japanese Journal of Physical Fitness and Sports Medicine 54, 353-361 [Google Scholar]
- Wu Q, Swain R. (2002) A mathematical model of the stability control of human thorax and pelvis movements during walking. Computer Methods in Biomechanics and Biomedical Engineer-ing 5, 67-74 [DOI] [PubMed] [Google Scholar]


