Robust Multi-Task Feature Learning

Abstract

Multi-task learning (MTL) aims to improve the performance of multiple related tasks by exploiting the intrinsic relationships among them. Recently, multi-task feature learning algorithms have received increasing attention and they have been successfully applied to many applications involving high-dimensional data. However, they assume that all tasks share a common set of features, which is too restrictive and may not hold in real-world applications, since outlier tasks often exist. In this paper, we propose a Robust MultiTask Feature Learning algorithm (rMTFL) which simultaneously captures a common set of features among relevant tasks and identifies outlier tasks. Specifically, we decompose the weight (model) matrix for all tasks into two components. We impose the well-known group Lasso penalty on row groups of the first component for capturing the shared features among relevant tasks. To simultaneously identify the outlier tasks, we impose the same group Lasso penalty but on column groups of the second component. We propose to employ the accelerated gradient descent to efficiently solve the optimization problem in rMTFL, and show that the proposed algorithm is scalable to large-size problems. In addition, we provide a detailed theoretical analysis on the proposed rMTFL formulation. Specifically, we present a theoretical bound to measure how well our proposed rMTFL approximates the true evaluation, and provide bounds to measure the error between the estimated weights of rMTFL and the underlying true weights. Moreover, by assuming that the underlying true weights are above the noise level, we present a sound theoretical result to show how to obtain the underlying true shared features and outlier tasks (sparsity patterns). Empirical studies on both synthetic and real-world data demonstrate that our proposed rMTFL is capable of simultaneously capturing shared features among tasks and identifying outlier tasks.

1. Introduction

Multi-task learning [8] aims to improve the performance of multiple related tasks by utilizing the intrinsic relationships among these tasks. Multi-task learning has been applied successfully in a wide range of applications including object recognition [8], speech recognition [28], handwritten digits recognition [30] and disease progression prediction [44]. A critical ingredient in these applications is how to model the shared structures among tasks. Existing algorithms can be broadly classified into two categories: explicit parameter sharing and implicit structure sharing.

Under explicit parameter sharing, all the tasks explicitly share some common parameters; examples include hidden units in neural networks [8, 5], prior in hierarchical Bayesian models [4, 31, 36, 38], parameters of Gaussian process [18], feature mapping matrix [1], classification weight [11] and similarity metric [28, 40]. On the contrary, algorithms under implicit structure sharing do not explicitly impose all tasks to share certain parameters, but they implicitly capture some common structures; for example, the algorithms in [29, 24] constrain all tasks to share a common low rank subspace and the algorithms in [27, 2, 23, 19, 22, 17, 35, 41] constrain all tasks to share a common set of features.

One key assumption of the above multi-task learning algorithms for both categories is that all tasks are related to each other by the presumed structures. However, this may not hold in real-world applications, as outlier tasks often exist. Thus, simply assuming that all tasks share a certain structure may degrade the performance. This motivates the development of several recent multi-task learning algorithms for discovering the inherent relationship among tasks. For example, some multi-task learning algorithms [32, 34, 14, 42, 16] cluster the given tasks into different groups and impose the tasks in the same groups to share a certain common structure. Multi-task learning algorithms with a composite regularization [15, 9, 10] have been proposed to capture different types of relationships using regularization.

In this paper, we consider the multi-task learning setting where the relevant tasks share a common set of features while outlier tasks exist. We propose a Robust Multi-Task Feature Learning algorithm (rMTFL) which simultaneously captures the shared features among relevant tasks and detects outlier tasks. Specifically, we decompose the weight matrix W consisting of the prediction models of all tasks into the sum of two components P and Q. We employ the well-known group Lasso penalty on row groups of P such that the relevant tasks capture a common set of features. In addition, we employ the same group Lasso penalty but on column groups of Q to simultaneously identify the outlier tasks. The main contributions of this paper include:

1. We propose a Robust Multi-Task Feature Learning formulation (rMTFL) which simultaneously captures a common set of features among relevant tasks and identifies outlier tasks. We propose to employ accelerated gradient descent to efficiently solve the optimization problem involved in rMTFL, and show that the proposed algorithm is scalable to large-size problems.

2. We present a theoretical bound to measure how well rMTFL can approximate the underlying true evaluation, and give bounds to measure the error between the weights estimated from rMTFL and the underlying true weights. Moreover, by assuming that the underlying true weights are above the noise level, we present a sound theoretical result to show how we can obtain the underlying true shared features and outlier tasks (sparsity patterns).

3. We perform empirical studies using both synthetic and real-world data. Our experiments demonstrate the efficiency of the proposed algorithm. Results also demonstrate the effectiveness of rMTFL for capturing shared features among tasks and identifying outlier tasks simultaneously.

Organization

The remainder of this paper is organized as follows: In Section 2, we introduce our proposed rMTFL formulation. In Section 3, we present the proposed optimization algorithm for rMTFL. In Section 4, we provide a detailed theoretical analysis on rMTFL. In Section 5, we discuss related work. Experimental results are presented in Section 6 and we conclude the paper in Section 7.

Notations

Scalars, vectors, matrices and sets are denoted by lower case letters, bold face lower case letters, capital letters and calligraphic capital letters, respectively. x_i and x_ij denote the i-th entry of a vector x and the (i, j)-th entry of a matrix X. xⁱ (x_i) denotes the i-th row (column) of a matrix X. ${\mathit{\text{X}}}^{\mathcal{\text{J}}}$ denotes a submatrix composed of the rows of X indexed by 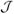. $x_{\mathit{\text{jk}}}^{(i)}$ and ${\mathbf{\text{x}}}_j^{(i)}$ denote the (j, k)-th entry and the j-th column of a matrix X_i. Euclidean and Frobenius norms are denoted by ‖ · ‖ and ‖ · ‖_F. ℓ_p,q-norm of a matrix X is defined as ${\Vert X\Vert }_{p,q}={\left({\sum }_i{\left({({\sum }_j{x}_{\mathit{\text{ij}}}^q)}^{1/q}\right)}^p\right)}^{1/p}$ and the inner product of X and Y is denoted by 〈X,Y〉. ℕ_m is defined as the set {1, …, m} and N(μ, σ²) denotes a normal distribution with mean μ and standard deviation σ.

2. The Proposed Formulation

Assume that we are given m learning tasks associated with the training data {(X₁, y₁),⋯, (X_m,y_m)}, where X_i ∈ ℝ^{d × n_i} is the data matrix of the i-th task with each column as a sample; y_i ∈ ℝ^n_i is the response of the i-th task (y_i has continuous values for regression and discrete values for classification); d is the data dimensionality; n_i is the number of samples for the i-th task. The data has been normalized such that the (j, k)-th entry of X_i denoted as $x_{\mathit{\text{jk}}}^{(i)}$ satisfies

$$\sum _{k=1}^{n_i}{\left(x_{\mathit{\text{jk}}}^{(i)}\right)}^2=1,\forall j\in {\mathbb{N}}_d.$$ (1)

We consider learning a linear function

$$y_{\mathit{\text{ji}}}\approx f_i\left({\mathbf{\text{x}}}_j^{(i)}\right)={\left({\mathbf{\text{x}}}_j^{(i)}\right)}^T{\mathbf{\text{w}}}_i,i\in {\mathbb{N}}_m,j\in {\mathbb{N}}_{n_i}$$

for each task and decomposing the weight matrix W = [w₁, ⋯, w_m] ∈ ℝ^{d × m} into the sum of two components P and Q (Please refer to Figure 1 for illustration). We make use of different regularization terms on P and Q to exploit relationships among tasks. Formally, our rMTFL model is formulated as:

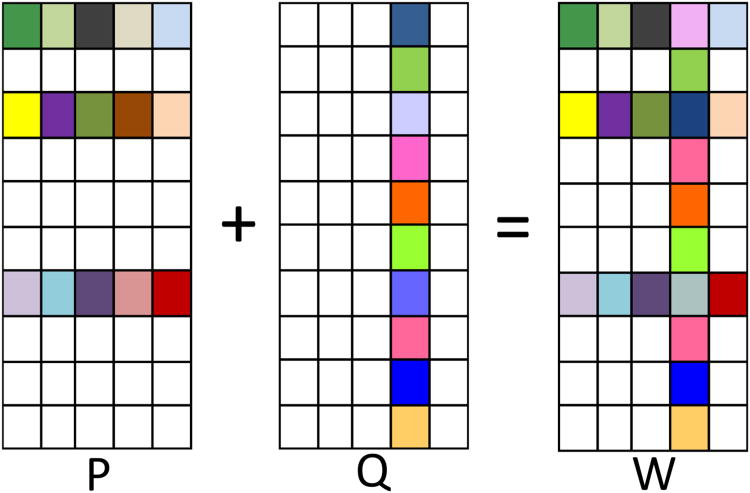
Figure 1.

Illustration of weight matrix decomposition for rMTFL, where squares with white background denote zero entries. There are 5 tasks, where the fourth task is an outlier task. Please refer to the text for detailed explanation.

$$\underset{W,P,Q}{\text{min}}\sum _{i=1}^m\frac{1}{m{n}_i}{\Vert X_i^T{\mathbf{\text{w}}}_i-{\mathbf{\text{y}}}_i\Vert }^2+{\lambda }_1{\Vert P\Vert }_{1,2}+{\lambda }_2{\Vert Q^T\Vert }_{1,2},s.t.W=P+Q,$$ (2)

where the first regularization term on P captures the shared features among tasks and the second term on Q discovers the outlier tasks; λ₁ and λ₂ are nonnegative parameters to control these two terms. Specifically, the first regularization term is based on the well-known group Lasso penalty on row groups of P which restricts the rows of the optimal solution P* to consist of all zero or nonzero elements [2]. Thus, all related tasks should select a common set of features. However, the assumption that all tasks share the same set of features may not hold in real applications, as outlier tasks often exist. To address this issue, we introduce the second regularization term based on the same group Lasso penalty but on column groups of Q to discover these outlier tasks. Similarly, the columns of the optimal solution Q* consist of all zero or nonzero elements, with the nonzero columns corresponding to outlier tasks. Intuitively, if the i-th column of Q* is nonzero, then the i-th column of W* is also nonzero, thus the i-th task does not share a common set of features with other tasks, identified as an outlier task; meanwhile, for the remaining tasks corresponding to the zero columns of Q*, they share a common set of features captured by the nonzero rows of P* (see Figure 1).

3. Optimization Algorithm

In this section, we show how to solve the rMTFL formulation in Eq. (2) efficiently. Denote

$$\begin{array}{c}l(P,Q)=\sum _{i=1}^m\frac{1}{m{n}_i}{\Vert X_i^T({\mathbf{\text{p}}}_i+{\mathbf{\text{q}}}_i)-{\mathbf{\text{y}}}_i\Vert }^2,\\ r(P,Q)={\lambda }_1{\Vert P\Vert }_{1,2}+{\lambda }_2{\Vert Q^T\Vert }_{1,2},\end{array}$$ (3)

where l(P, Q) is the empirical loss function and r(P, Q) is the regularization term. We note that the objective function in Eq. (2) is a composite function of a differential term l(P, Q) and a non-differential term r(P, Q). Denote

$$T_{R,S,\eta }(P,Q)=l(R,S)+\langle \frac{\partial l(R,S)}{\partial R},P-R\rangle +\frac{\eta }{2}{\Vert P-R\Vert }_F^2+\langle \frac{\partial l(R,S)}{\partial S},Q-S\rangle +\frac{\eta }{2}{\Vert Q-S\Vert }_F^2,$$ (4)

which is the first order Taylor expansion of l(P, Q) at (R, S), with the squared Euclidean distance between (P, Q) and (R, S) as the regularization term. The traditional gradient descent algorithm obtains the solution at the k-th iteration (k ≥ 1) by (P^k, Q^k) = arg min_P,Q T_{P^k–1, Q^k–1,ηk} (P,Q) + r(P, Q) with a proper step size η_k. Here we propose to employ the accelerated gradient descent [25, 26] to solve the optimization problem, which generates the solution at the k-th iteration (k ≥ 1) by computing the following proximal operator [20, 19, 21, 12, 37, 3]:

$$(P^k,Q^k)=\underset{P,Q}{\text{arg min}}{T}_{R^k,S^k,{\eta }_k}(P,Q)+r(P,Q),$$ (5)

where R¹ = P⁰,S¹ = Q⁰ and R^k+1 = P^k + α_k(P^k − P^{k – 1}), S^{k + 1} = Q^k + α_k(Q^k − Q^k–1) for k ≥ 1; η_k (k ≥ 1) is set by finding the smallest nonnegative integer m_k such that with η_k = 2^m_k η_k–1:

$$l(P^k,Q^k)\le T_{R^k,S^k,{\eta }_k}(P^k,Q^k).$$ (6)

We note that (R^k+1,S^{k +1}) is in fact a linear combination of (P^k,Q^k) and (P^{k –1},Q^{k –1}). The coefficient α_k plays an important role in the convergence of the algorithm. As suggested by [6], we set α_k = (t_k–1 − 1)/t_k, where t₀ = 1 and $t_k=(1+\sqrt{t_{k-1}^2+1})/2$ for k ≥ 1. According to the theoretical analysis in [6], we present the following convergence result for rMTFL:

Theorem 1. Let (P^k, Q^k) be generated by Eq. (5) with a properly chosen η_k satisfying Eq. (6). Then for any k ≥ 1,

$$f(P^k,Q^k)-f(P\ast ,Q\ast )=O\left(\frac{1}{k^2}\right),$$ (7)

where f(·, ·) and (P*,Q*) are respectively the objective function and the optimal solution in Eq. (2).

3.1 Implementation details

There are two issues that remain to be addressed: how to compute the proximal operator in Eq. (5) and how to select a proper initial value η₀.

Due to the decomposable property of Eq. (5), we can cast Eq. (5) into the following two separate proximal operator problems:

$$\begin{array}{c}{P}^k=\underset{P}{\text{arg min}}\frac{1}{2}{\Vert P-(R^k-\frac{1}{{\eta }_k}{\nabla }_{R}l(R^k,S^k))\Vert }_F^2+\frac{{\lambda }_1}{{\eta }_k}{\Vert P\Vert }_{1,2}\\ Q^k=\underset{Q}{\text{arg min}}\frac{1}{2}{\Vert Q-(S^k-\frac{1}{{\eta }_k}{\nabla }_{S}l(R^k,S^k))\Vert }_F^2+\frac{{\lambda }_2}{{\eta }_k}{\Vert Q^T\Vert }_{1,2}\end{array}$$

where ∇_Rl(R^k,S^k) and ∇_Sl(R^k,S^k) are the partial derivatives of l(R,S) with respect to S and R at (R^k,S^k). The above proximal operator problems admit closed form solutions with time complexity of O(dm)[19]:

$$\begin{array}{c}{\left({\mathbf{\text{p}}}^{(k)}\right)}^i=\text{max}(0,1-\frac{{\lambda }_1}{{\eta }_k\Vert {({\mathbf{\text{u}}}^{(k)})}^i\Vert }){\left({\mathbf{\text{u}}}^{(k)}\right)}^i,\forall i\in {\mathbb{N}}_d,\\ {\mathbf{\text{q}}}_j^{(k)}=\text{max}(0,1-\frac{{\lambda }_2}{{\eta }_k\Vert {\mathbf{\text{v}}}_j^{(k)}\Vert }){\mathbf{\text{v}}}_j^{(k)},\forall j\in {\mathbb{N}}_m,\end{array}$$

where $U^k=R^k-\frac{1}{{\eta }_k}{\nabla }_{R}l(R^k,S^k),V^k=S^k-\frac{1}{{\eta }_k}{\nabla }_{S}l(R^k,S^k);{\left({\mathbf{\text{u}}}^{(k)}\right)}^i$ and ${\mathbf{\text{v}}}_j^{(k)}$ denote the i-th row of U^k and the j-th column of V^k, respectively.

An appropriate choice for η₀ is the Lipschitz constant L of the gradient of l(P,Q). However, the Lipschitz constant L is unknown and calculating it is computationally expensive. Next, we show how to estimate its lower and upper bounds. Denote by $D\in {ℝ}^{\mathit{\text{dm}}\times ({\sum }_{i=1}^m{n}_i)}$ a block diagonal matrix with $\sqrt{\frac{2}{m{n}_i}}{X}_i(i\in {\mathbb{N}}_m)$ as the i-th block. Then the Lipschitz constant L is just the squared maximum singular value of D. According to matrix norm properties [13], we can bound L as follows:

$$\text{min}(\frac{{\Vert D\Vert }_{\infty ,1}^2}{{\sum }_{i=1}^m{n}_i},\frac{{\Vert D^T\Vert }_{\infty ,1}^2}{dm})\le L\le {\Vert D\Vert }_{\infty ,1}{\Vert D^T\Vert }_{\infty ,1}.$$ (8)

We note that D is a block diagonal matrix and it is sparse when m (the number of tasks) is large, which makes the bounds of L very tight. If we set η₀ as the upper bound of L, then we do not need line search, because when η_k ≥ L, Eq. (6) is always satisfied [6]. Otherwise, line search is necessary. Although setting η₀ as the upper bound of L can eliminate line search, it may increase the outer iterative steps. On the contrary, it leads to a smaller outer iterative steps by setting η₀ as the lower bound of L. In our experiments, we use the lower bound of L to initialize η.

4. Theoretical Analysis

4.1 Basic Assumption

We assume that the responses are given by a linear model plus Gaussian noise¹, i.e.,

$$y_{\mathit{\text{ji}}}=f_i^{\ast }\left({\mathbf{\text{x}}}_j^{(i)}\right)+{\delta }_{\mathit{\text{ji}}}={\left({\mathbf{\text{x}}}_j^{(i)}\right)}^T{\mathbf{\text{w}}}_i^{\ast }+{\delta }_{\mathit{\text{ji}}},i\in {\mathbb{N}}_m,j\in {\mathbb{N}}_n,$$ (9)

where W* is the true weight matrix decomposed as the sum of two underlying true components P* and Q*:

$$W\ast =[{\mathbf{\text{w}}}_1^{\ast },\cdots ,{\mathbf{\text{w}}}_m^{\ast }]=P\ast +Q\ast \in {ℝ}^{d\times m};$$ (10)

$$X_i={[{\mathbf{\text{x}}}_1^{(i)},\cdots ,{\mathbf{\text{x}}}_n^{(i)}]}^T\in {ℝ}^{d\times n},{\mathbf{\text{y}}}_i={[y_{1i},\cdots ,y_{\mathit{\text{ni}}}]}^T\in {ℝ}^n$$ (11)

are respectively the training data and responses of the i-th task;

$${\mathit{\text{δ}}}_i={[{\delta }_{1i},\cdots ,{\delta }_{\mathit{\text{ni}}}]}^T\in {ℝ}^n,{\delta }_{\mathit{\text{ji}}}\sim N(0,{\sigma }^2),i\in {\mathbb{N}}_m,j\in {\mathbb{N}}_n,$$ (12)

$${\mathbf{\text{f}}}_i^{\ast }=X_i^T{\mathbf{\text{w}}}_i^{\ast }={\left[f_i^{\ast }\right({\mathbf{\text{x}}}_1^{(i)}),\cdots ,f_i^{\ast }({\mathbf{\text{x}}}_n^{(i)}\left)\right]}^T\in {ℝ}^n$$ (13)

are the i.i.d. normal noise and the true evaluation, respectively. Thus, we have

$${\mathbf{\text{y}}}_i={\mathbf{\text{f}}}_i^{\ast }+{\mathit{\text{δ}}}_i,i\in {\mathbb{N}}_m.$$ (14)

We also define

$$\mathcal{\text{J}}(P)=\{i|{\mathbf{\text{p}}}^i\ne \mathbf{0}\},{\mathcal{\text{J}}}_{\perp }(P)=\{i|{\mathbf{\text{p}}}^i=\mathbf{0}\}$$ (15)

as the index sets for the nonzero and zero rows of P.

4.2 Theoretical Bounds

The following theorem provides a key property of the optimal solution of Eq. (2), which is critical for our subsequent theoretical analysis:

Theorem 2. Let (P̂, Q̂) be an optimal solution of Eq. (2) for m ≥ 2 and n, d ≥ 1. Let X_i and y_i be defined in Eq. (11); let δ_i and ${\mathbf{\text{f}}}_{\mathit{\text{i}}}^{\ast }$ be defined in Eq. (12) and Eq. (13), respectively. We assume that the data is normalized as in Eq. (1). Choose the regularization parameters λ₁ and λ₂ as

$${\lambda }_1,{\lambda }_2\ge \alpha ,\alpha =\frac{2\sigma }{\mathit{\text{mn}}}\sqrt{\mathit{\text{dm}}+t},$$ (16)

where t is a positive scalar. Then with probability of at least $1-\text{exp}(-\frac{1}{2}(t-\mathit{\text{dm}}\text{log}(1+\frac{t}{\mathit{\text{dm}}})))$, for any P,Q ∈ ℝ^{d × m}, we have

$$\sum _{i=1}^m\frac{1}{\mathit{\text{mn}}}{\Vert X_i^T({\widehat{\mathbf{\text{p}}}}_i+{\widehat{\mathbf{\text{q}}}}_i)-{\mathbf{\text{f}}}_i^{\ast }\Vert }^2\le \sum _{i=1}^m\frac{1}{\mathit{\text{mn}}}{\Vert X_i^T({\mathbf{\text{p}}}_i+{\mathbf{\text{q}}}_i)-{\mathbf{\text{f}}}_i^{\ast }\Vert }^2+2{\lambda }_1{\Vert {(\widehat{P}-P)}^{\mathcal{\text{J}}(P)}\Vert }_{1,2}+2{\lambda }_2{\Vert {({\widehat{Q}}^T-Q^T)}^{\mathcal{\text{J}}(Q^T)}\Vert }_{1,2}.$$ (17)

Based on Theorem 2, we present some performance bounds of our rMTFL model in Eq. (2). We first introduce some notations to unclutter the equations. Let X ∈ ℝ^{dm × mn} be a block diagonal matrix with X_i ∈ ℝ^{d × n} (i ∈ ℕ_m) as the i-th block. Define a vectorization operator ‘vec’ over an arbitrary matrix A ∈ ℝ^{d × m} such that $\text{vec}(A)={[{\mathbf{\text{a}}}_1^T,\cdots ,{\mathbf{\text{a}}}_m^T]}^T$. Then, Eq. (17) can be rewritten as

$$\frac{1}{\mathit{\text{mn}}}{\Vert X^T\text{vec}(\widehat{P}+\widehat{Q})-\text{vec}(F\ast )\Vert }^2\le \frac{1}{\mathit{\text{mn}}}{\Vert X^T\text{vec}(P+Q)-\text{vec}(F\ast )\Vert }^2+2{\lambda }_1{\Vert {(\widehat{P}-P)}^{\mathcal{\text{J}}(P)}\Vert }_{1,2}+2{\lambda }_2{\Vert {({\widehat{Q}}^T-Q^T)}^{\mathcal{\text{J}}(Q^T)}\Vert }_{1,2},$$ (18)

where $F\ast =[{\mathbf{\text{f}}}_1^{\ast },\cdots ,{\mathbf{\text{f}}}_m^{\ast }]\in {ℝ}^{n\times m}$. Next, we make the following assumption about the training data and the weight matrix, which generalizes the restricted eigenvalue assumption in [7].

Assumption 1. For a matrix pair Γ_P ∈ ℝ^{d × m} and Γ_Q ∈ ℝ^{d × m}, let r and c (1 ≤ r ≤ d, 1 ≤ c ≤ m) be the upper bounds of | 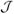(P*)| and | 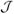(Q*^T)|, respectively, and let β₁ and β₂ be positive scalars. We assume that there exist positive scalars κ₁(r) and κ₂(c) such that

$${\kappa }_1(r)=\underset{{\Gamma }_P,{\Gamma }_Q\in \mathcal{\text{R}}(r,c)}{\text{min}}\frac{\Vert X^T\text{vec}({\Gamma }_P+{\Gamma }_Q)\Vert }{\sqrt{\mathit{\text{mn}}}{\Vert {({\Gamma }_P)}^{\mathcal{\text{J}}(P)}\Vert }_F}$$ (19)

$${\kappa }_2(c)=\underset{{\Gamma }_P,{\Gamma }_Q\in \mathcal{\text{R}}(r,c)}{\text{min}}\frac{\Vert X^T\text{vec}({\Gamma }_P+{\Gamma }_Q)\Vert }{\sqrt{\mathit{\text{mn}}}{\Vert {({\Gamma }_Q^T)}^{\mathcal{\text{J}}(Q^T)}\Vert }_F},$$ (20)

where the set 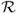(r, c) is defined as

$$\mathcal{\text{R}}(r,c)=\{{\Gamma }_P,{\Gamma }_Q\in {ℝ}^{d\times m}|{\Gamma }_P\ne 0,{\Gamma }_Q\ne 0,|\mathcal{\text{J}}(P)|\le r,|\mathcal{\text{J}}(Q^T)|\le c,{\Vert {({\Gamma }_P)}^{\mathcal{\text{J}}\perp (P)}\Vert }_{1,2}\le {\beta }_1{\Vert {({\Gamma }_P)}^{\mathcal{\text{J}}(P)}\Vert }_{1,2},{\Vert {({\Gamma }_Q^T)}^{\mathcal{\text{J}}\perp (Q^T)}\Vert }_{1,2}\le {\beta }_2{\Vert {({\Gamma }_Q^T)}^{\mathcal{\text{J}}(Q^T)}\Vert }_{1,2}\},$$

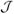(·) is defined in Eq. (15) and | 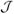| denotes the number of elements in the set .

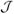Note that Assumption 1 is related to the restricted eigenvalue assumption which is a critical condition in [7]. Some previous studies on multi-task learning [22, 10] also make use of similar assumptions. Our main theoretical result is summarized in the following theorem for performance bounds.

Theorem 3. Let (P̂, Q̂) be an optimal solution of Eq. (2) for m ≥ 2 and n, d ≥ 1 and take the regularization parameters λ₁ and λ₂ as in Eq. (16). Then under Assumption 1, the following results hold with probability of at least $1-\text{exp}(-\frac{1}{2}(t-\mathit{\text{dm}}\text{log}(1+\frac{t}{\mathit{\text{dm}}})))(t>0)$:

$$\frac{1}{\mathit{\text{mn}}}{\Vert X^T\text{vec}(\widehat{P}+\widehat{Q})-\text{vec}(F\ast )\Vert }^2\le {(\frac{2{\lambda }_1\sqrt{r}}{{\kappa }_1(r)}+\frac{2{\lambda }_2\sqrt{c}}{{\kappa }_2(c)})}^2,$$ (21)

$${\Vert \widehat{P}-P\ast \Vert }_{1,2}\le \frac{({\beta }_1+1)\sqrt{r}}{{\kappa }_1(r)}(\frac{2{\lambda }_1\sqrt{r}}{{\kappa }_1(r)}+\frac{2{\lambda }_2\sqrt{c}}{{\kappa }_2(c)}),$$ (22)

$${\Vert {\widehat{Q}}^T-Q{\ast }^T\Vert }_{1,2}\le \frac{({\beta }_2+1)\sqrt{c}}{{\kappa }_2(c)}(\frac{2{\lambda }_1\sqrt{r}}{{\kappa }_1(r)}+\frac{2{\lambda }_2\sqrt{c}}{{\kappa }_2(c)}).$$ (23)

If in addition, the following conditions hold:

$$\underset{j\in \mathcal{\text{J}}(P\ast )}{\text{min}}\Vert {(\mathbf{\text{p}}\ast )}^j\Vert >\frac{2({\beta }_1+1)\sqrt{r}}{{\kappa }_1(r)}(\frac{2{\lambda }_1\sqrt{r}}{{\kappa }_1(r)}+\frac{2{\lambda }_2\sqrt{c}}{{\kappa }_2(c)}),$$ (24)

$$\underset{j\in \mathcal{\text{J}}(Q{\ast }^T)}{\text{min}}\Vert {(\mathbf{\text{q}}\ast )}_j\Vert >\frac{2({\beta }_2+1)\sqrt{c}}{{\kappa }_2(c)}(\frac{2{\lambda }_1\sqrt{r}}{{\kappa }_1(r)}+\frac{2{\lambda }_2\sqrt{c}}{{\kappa }_2(c)}),$$ (25)

then with the same probability, the following two sets

$${\widehat{\mathcal{\text{J}}}}_1=\{j|\Vert {\widehat{\mathbf{\text{p}}}}^j\Vert >\frac{({\beta }_1+1)\sqrt{r}}{{\kappa }_1(r)}(\frac{2{\lambda }_1\sqrt{r}}{{\kappa }_1(r)}+\frac{2{\lambda }_2\sqrt{c}}{{\kappa }_2(c)})\},$$ (26)

$${\widehat{\mathcal{\text{J}}}}_2=\{j|\Vert {\widehat{\mathbf{\text{q}}}}_j\Vert >\frac{({\beta }_2+1)\sqrt{c}}{{\kappa }_2(c)}(\frac{2{\lambda }_1\sqrt{r}}{{\kappa }_1(r)}+\frac{2{\lambda }_2\sqrt{c}}{{\kappa }_2(c)})\}$$ (27)

estimate the true sparsity pattern 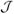(P*) and 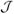(Q*^T), respectively. That is,

$${\widehat{\mathcal{\text{J}}}}_1=\mathcal{\text{J}}(P\ast ),$$ (28)

$${\widehat{\mathcal{\text{J}}}}_2=\mathcal{\text{J}}(Q{\ast }^T).$$ (29)

Theorem 3 provides important theoretical guarantee for rMTFL. Specifically, these bounds not only measure how well our rMTFL model can approximate the true evaluation values defined in Eq. (9) [Eq. (21)], but also measure how well our rMTFL model can approximate the true weight matrices (P*,Q*,W* = P* + Q*) [Eq. (22) and Eq. (23)]. Moreover, under the assumption that the underlying true weights are above the noise level [Eq. (24) and Eq. (24)], we can also estimate the true sparsity patterns (i.e., 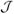(P*), 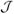(Q*^T)) with high probability [Eq. (26) and Eq. (27)].

5. Related Work

Previous studies in [15, 9, 10] also decompose the weight matrix into two components; rMTFL differs from these work in several aspects:

1. rMTFL employs different regularization terms from the algorithms in [15, 9, 10]. The regularization terms in rMTFL not only have intuitive explanations for feature selection and outlier tasks detection (see Figure 1 and detailed explanation in Section 2), but also have sound theoretical guarantee (see Section 4).

2. rMTFL has the mechanism of detecting outlier tasks, unlike the algorithms in [15, 9]. Although the algorithm in [10] has the ability to detect the outlier, it focuses on capturing the low rank structure among tasks, while rMTFL has advantages on high dimensional multi-task feature learning problems. Specifically, in terms of the evaluation performance, the main difference between our Theorem 2 and Lemma 4.3 in [10] is that the bound of rMTFL is based on ${\Vert {(\widehat{P}-P)}^{\mathcal{\text{J}}(P)}\Vert }_{1,2}$, while the bound of RMTL in [10] is based on ║Q(L̂ − L)║_tr. In practical multi-task learning problems, the dimensionality is often high and the underlying selected features are few, that is, the number of elements in 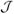(P) can be small, which indicates that ${\Vert {(\widehat{P}-P)}^{\mathcal{\text{J}}(P)}\Vert }_{1,2}$ is small, leading to a tight bound in Theorem 2. However, in the scenario of a large number of tasks, the relevant tasks may share a low rank subspace, resulting in a small value of ║Q(L̂ −L)║_tr. Therefore, rMTFL has an advantage of identifying a few shared features for high dimensional data, while RMTL in [10] focuses on discovering low rank subspace among a large number of tasks. Our experimental results in Section 6.4 demonstrate that rMTFL outperforms RMTL in the high dimensional scenario, and RMTL is preferred when the number of tasks is large but the dimensionality is low.

3. Unlike the analysis in [10], we provide theoretical bounds to measure the error between the estimated weights of rMTFL and the underlying true weights. Moreover, we have theoretically shown under what conditions we can obtain the underlying true shared features and outlier tasks (sparsity patterns). In addition, both Theorem 2 and Theorem 3 work with probability of at least $1-\text{exp}(-\frac{1}{2}(t-\mathit{\text{dm}}\text{log}(1+\frac{t}{\mathit{\text{dm}}})))$ which is higher than $1-m\text{exp}(-\frac{1}{2}(t-d\text{log}(1+\frac{t}{d})))$ presented in Lemma 4.3 and Theorem 4.1 of [10].

4. Each step of the optimization method in [10] involves SVD operation with a time complexity of O(min(d²m, m²d)), thus it does not scale to large-size problems (e.g., the number of tasks and the dimensionality are large). As we show in Section 3.1, the optimization method of rMTFL has a much lower time complexity of O(dm) and hence can be applied to large-size problems.

6. Experiments

6.1 Competing Algorithms and Data Sets

Competing Algorithms

We compare our rMTFL algorithm on multi-task regression problems with seven representative algorithms: ridge multi-task regression (ridge), ℓ₁-norm multi-task regression (lasso), trace-norm multi-task regression (trace), ℓ_1,2-norm multi-task regression (L1,2), dirty model multi-task regression (DirtyMTL) [15], sparse structures and low rank multi-task regression (SLR) [9] and robust multi-task regression (RMTL) [10]. All eight algorithms employ a quadratic loss function. Matlab codes of the rMTFL algorithm are available online [43].

Synthetic data

The synthetic data is generated as follows: we set the number of tasks m = 30 and each task has n_i = 200 samples in d = 200 dimension; each entry of the data matrix X_i ∈ ℝ^{d × n_i}(i ∈ ℕ_m) is sampled from the distribution N(0,25) and it is normalized such that Eq. (1) is satisfied; each entry of the ground truth weight matrices P ∈ ℝ^{d × m} and Q ∈ ℝ^{d × m} is generated from the distribution N(0,64); we set the first 160 rows of P and the first 20 columns of Q as zero vectors; the elements of the noise vector δ_i ∈ ℝ^n_i(i ∈ N_m) are sampled from the distribution N(0,1); the response y_i ∈ ℝ^n_i(i ∈ ℕ_m) is computed via ${\mathbf{\text{y}}}_i=X_i^T(P+Q)+{\mathit{\text{δ}}}_i$. Under this setting, we have constructed 20 related tasks and 10 outlier tasks.

Real-world Data

We adopt two data sets for our multitask regression evaluation: School data² and MRI data.

The School data set is from the Inner London Education Authority (ILEA), consisting of examination records of 15362 students (samples) from 139 secondary schools in years 1985, 1986 and 1987. Each sample is represented by 27 binary attributes which include year, gender, examination score, etc., plus 1 bias attribute (In our experiments, the bias attribute is not used). The response (target) is the examination score. So we have 139 tasks with each task corresponding to one school.

The MRI data set is from the ANDI database. It contains MRI data of 675 patients preprocessed using FreeSurfer³. The MRI data include 306 features which can be categorized into 5 types: cortical thickness average, cortical thickness standard deviation, volume of cortical parcellation, volume of white matter parcellation, and surface area. The response (target) is the Mini Mental State Examination (MMSE) score coming from 6 different time points: M06, M12, M18, M24, M36, and M48. We remove the samples which fail the MRI quality controls and with missing entries. After the preprocessing above, we have 6 tasks with each task corresponding to a time point and the sample sizes corresponding to 6 tasks are 648, 642, 293, 569, 389 and 87, respectively.

6.2 Experimental Setting

In our experiments, we terminate all the algorithms when the relative change of the two consecutive objective function values is less than 10⁻⁵. We randomly split the samples (both synthetic and real-world data sets) from each task into training and test samples with different training ratios. We evaluate eight multi-task regression algorithms on the test data set, using normalized mean squared error (nMSE) and averaged means squared error (aMSE) as the regression performance measures [39, 10, 42]. For each training ratio, both nMSE and aMSE are averaged over 10 random splittings of training and test sets. All parameters of the eight algorithms are tuned via 3-fold cross validation.

6.3 Synthetic Data Experiments

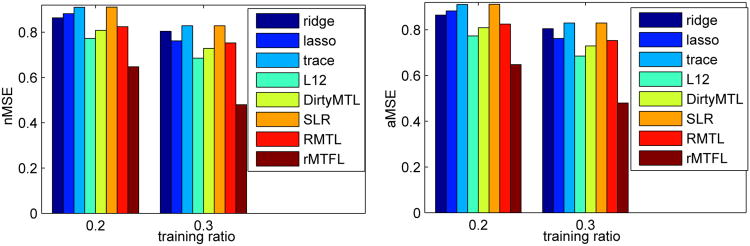
We set the training ratio of synthetic data generated in Section 6.1 as 20% and 30%, respectively. Experimental results (averaged nMSE and aMSE) are shown in Figure 2. We observe that rMTFL outperforms all the other competing algorithms, which demonstrates the effectiveness of rMTFL for high dimensional problems with outlier tasks.

Figure 2.

Averaged test error (nMSE and aMSE) vs. training ratio for synthetic data.

6.3.1 Illustration of Outlier Tasks Detection

Next, we further demonstrate the outlier tasks detection capability of rMTFL. We firstly generate another synthetic data set following the same procedure in Section 6.1, except that each task has n_i = 20 samples. Then, we set ${\lambda }_1=2\sqrt{\mathit{\text{dm}}+t}/{\sum }_{i=1}^m{n}_i,{\lambda }_2=6\sqrt{\mathit{\text{dm}}+t}/{\sum }_{i=1}^m{n}_i,t={10}^{-10}$ and run rMTFL on this synthetic data until the relative change of the two consecutive objective function values is less than 10⁻⁵. Figure 3 shows the results of P and Q obtained by rMTFL. Specifically, there are 164 zero rows in P and 21 zero columns in Q. These results demonstrate the capability of rMTFL in simultaneously capturing the shared features among tasks (the nonzero rows of P) and discovering outlier tasks (the nonzero columns of Q).

Figure 3.

Figures of P, Q and W = P + Q generated from rMTFL on the synthetic data. Black points correspond to zero entries. Note that the figures are clockwise rotated 90 degrees.

6.3.2 Scalability Studies on rMTFL

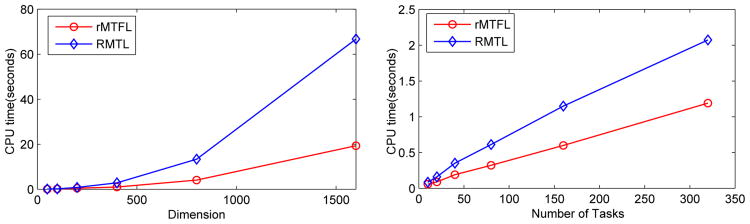
We conduct scalability studies on two algorithms which are capable of identifying outlier tasks: rMTFL and RMTL [10], when the dimension and the number of tasks increase. We firstly fix m = 20 and let the dimension d increase as {50ⁱ},i = 0,⋯,5. Then we run rMTFL and RMTL on the synthetic data generated following the same procedure in Section 6.1. The computational time (CPU time) vs. dimension plot is shown in the left subfigure of Figure 4. Similarly, we fix d = 100 and let the number of tasks m increase as {10ⁱ},i = 0, ⋯, 5. Then we run rMTFL and RMTL and show the computational time (CPU time) vs. the number of tasks plot as in the right subfigure of Figure 4. We observe that, the CPU time of both rMTFL and RMTL increases when the dimension d (or the number of tasks m) increases. However, the CPU time of RMTL increases significantly faster than rMTFL. Because the SVD computation with a time complexity of O(min(d²m,m²d)) involved at each step of RMTL is computationally much more expensive than the computation of the ℓ_1,2-norm proximal operator with a time complexity of O(dm) involved at each step of rMTFL. This demonstrates the superior scalability of rMTFL over RMTL.

Figure 4.

CPU time vs. dimension (left) and number of tasks (right) plots for rMTFL and RMTL. The CPU time is averaged over 10 independent runs.

6.4 Real-world Data Experiments

For the School data set, we respectively set the training ratio as 16%, 24%, 32%, and for the MRI data set, we respectively set the training ratio as 15%,20%,25%. Table 1 and Table 2 show the experimental results in terms of averaged nMSE and aMSE.

Table 1.

Comparison of eight multi-task regression algorithms on the MRI data set in terms of averaged nMSE and aMSE.

measure	traning ratio	ridge	lasso	trace	L1,2	DirtyMTL	SLR	RMTL	rMTFL
nMSE	0.15	0.9494	0.6469	0.6889	0.6445	0.6355	0.6905	0.6930	0.5743
	0.20	0.9355	0.6242	0.6629	0.6555	0.6231	0.6648	0.6557	0.5700
	0.25	0.9151	0.6015	0.6230	0.6446	0.6082	0.6244	0.6239	0.5498
aMSE	0.15	0.0270	0.0188	0.0195	0.0184	0.0177	0.0196	0.0196	0.0168
	0.20	0.0262	0.0177	0.0184	0.0184	0.0172	0.0185	0.0182	0.0163
	0.25	0.0255	0.0170	0.0171	0.0181	0.0167	0.0171	0.0171	0.0157

Table 2.

Comparison of eight multi-task regression algorithms on the School data set in terms of averaged nMSE and aMSE.

measure	traning ratio	ridge	lasso	trace	L1,2	DirtyMTL	SLR	RMTL	rMTFL
nMSE	0.16	1.2325	1.0457	0.7829	0.9236	0.8989	0.7812	0.7804	0.8628
	0.24	1.0734	0.9441	0.7606	0.9017	0.8413	0.7608	0.7613	0.8173
	0.32	0.9996	0.8875	0.7506	0.8972	0.8019	0.7507	0.7504	0.7874
aMSE	0.16	0.3154	0.2735	0.2048	0.2395	0.2358	0.2044	0.2041	0.2252
	0.24	0.2773	0.2469	0.1993	0.2341	0.2203	0.1993	0.1995	0.2135
	0.32	0.2580	0.2312	0.1958	0.2316	0.2088	0.1958	0.1958	0.2049

From these results, we have the following observations: (1) rMTFL outperforms all the other algorithms on the MRI data set. This may be due to the fact that for the MRI data set, the dimension (d = 306) is high especially when compared with the number of tasks (m = 6). (2) For the School data set, the multi-task learning algorithms based on trace norm (low rank) regularization (trace, SLR, RMTL) outperform the multi-task learning algorithms based on ℓ_1,q-norm (feature selection) regularization (lasso, L1,2, DirtyMTL, rMTFL). This may be due to the fact that the number of tasks (m = 139) of the School data set is larger compared with dimension (d = 27). In this case, restricting all tasks to share a low rank subspace is more reasonable than restricting all tasks to share a few common features. (3) On both data sets, the performance of rMTFL is the best among the feature selection based multi-task learning algorithms (lasso, L1,2, DirtyMTL, rMTFL). This may be due to rMTFL's capability of simultaneously discovering the shared features and identifying outlier tasks.

6.4.1 Outlier Tasks Detection

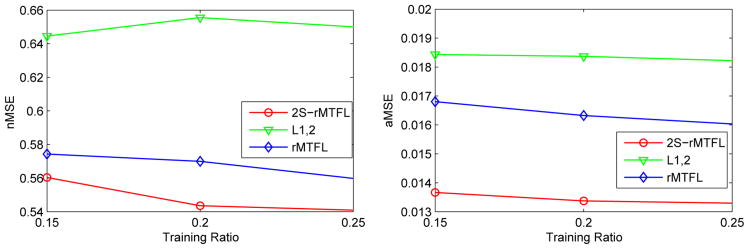
The proposed rMTFL algorithm is capable of capturing the shared features among tasks and detecting outlier tasks. We next evaluate the outlier tasks detection performance on the MRI data set. Firstly, we run rMTFL on the whole MRI data set and observe that the fourth task is identified as an outlier task. Then, we remove the fourth task, obtaining a new multi-task regression problem with the remaining 5 tasks. Finally, we run ℓ_1,2-norm multi-task regression on this ‘clean’ multi-task regression problem. We call this two-stage procedure as 2S-rMTFL. The test errors (nMSE and aMSE) on the MRI data set are shown in Figure 5. We can clearly see that after removing the outlier tasks, 2S-rMTFL outperforms L1,2 and rMTFL, which demonstrates the effectiveness of rMTFL in detecting outlier tasks.

Figure 5.

Test errors (nMSE and aMSE) on the MRI data set. See the texts for more details.

7. Conclusions

In this paper, we propose a Robust Multi-Task Feature Learning algorithm (rMTFL) to simultaneously capture the shared features among multiple related tasks and detect outlier tasks. We analyze the theoretical properties of rMTFL. Our analysis shows how well rMTFL can approximate the true evaluation, and measure how well rMTFL can approximate the underlying true weights. Moreover, we show that rMTFL can obtain the true sparsity patterns if the underlying true weights are above the noise level. In addition, the optimization problem involved in rMTFL can be solved efficiently, and rMTFL scales to large-size problems. In the future work, we will extend our rMTFL algorithm to multitask learning problems with general loss functions and apply rMTFL to other real-world applications.

Appendix

To prove the theorems presented in Section 4.2, we first provide some basic lemmas and then give the detailed proof.

Lemma 1. For any matrix pair P,P̂ ∈ ℝ^{d × m}, we have the following inequality:

$${\Vert \widehat{P}-P\Vert }_{1,2}+{\Vert P\Vert }_{1,2}-{\Vert \widehat{P}\Vert }_{1,2}\le 2{\Vert {(\widehat{P}-P)}^{\mathcal{\text{J}}(p)}\Vert }_{1,2},$$ (30)

Proof. According to Eq. (15),we have

$$P^{\mathcal{\text{J}}\perp (p)}=0,{\Vert {(\widehat{P}-P)}^{\mathcal{\text{J}}\perp (p)}\Vert }_{1,2}={\Vert {\widehat{P}}^{\mathcal{\text{J}}\perp (p)}\Vert }_{1,2}.$$

It follows that

$${\Vert {(\widehat{P}-P)}^{\mathcal{\text{J}}\perp (p)}\Vert }_{1,2}+{\Vert P\Vert }_{1,2}-{\Vert \widehat{P}\Vert }_{1,2}={\Vert {\widehat{P}}^{\mathcal{\text{J}}\perp (p)}\Vert }_{1,2}+{\Vert P\Vert }_{1,2}-{\Vert \widehat{P}\Vert }_{1,2}\le {\Vert {(\widehat{P}-P)}^{\mathcal{\text{J}}(p)}\Vert }_{1,2}$$ (31)

We note that ${\Vert \widehat{P}-P\Vert }_{1,2}={\Vert {(\widehat{P}-P)}^{\mathcal{\text{J}}(P)}\Vert }_{1,2}+{\Vert {(\widehat{P}-P)}^{\mathcal{\text{J}}\perp (P)}\Vert }_{1,2}$. Substituting Eq. (31) into Eq. (30), we verify Lemma 1.

Lemma 2. Let δ_i be I.I.D. random variables with δ_i ∼ N(0,σ²), i ∈ ℕ_n and ${\sum }_{i=1}^n{\alpha }_i^2=1$. Then we have

$$\upsilon =\frac{1}{\sigma }\sum _{i=1}^n{\alpha }_i{\delta }_i$$

is a standard normal random variable, i.e., υ ∼ N(0,1).

Proof. Since δ_i are I.I.D. random variables with δ_i ∼ N(0, σ²), i∈ ℕ_n, υ must be a normal random variable. Next, we need to show that the mean (E) and variance (V) of υ are respectively 0 and 1, as given below:

$$\begin{array}{c}\mathbb{\text{E}}(\upsilon )=\mathbb{\text{E}}\left(\frac{1}{\sigma }\sum _{i=1}^n{\alpha }_i{\delta }_i\right)=\frac{1}{\sigma }\sum _{i=1}^n{\alpha }_i\mathbb{\text{E}}({\delta }_i)=0,\\ \mathbb{\text{V}}(\upsilon )=\mathbb{\text{E}}({\upsilon }^2)=\frac{1}{{\sigma }^2}\sum _{i=1}^n{\alpha }_i^2\mathbb{\text{E}}({\delta }_i^2)=1.\end{array}$$

Lemma 3. Let χ²(d) be a chi-squared random variable with d degrees of freedom. Then, the following holds:

$$\text{Pr}({\chi }^2(d)\ge d+t)\le \text{exp}(-\frac{1}{2}(t-d\text{log}(1+\frac{t}{d})\left)\right),t>0.$$

Proof. By the Wallace inequality [33], we obtain

$$\text{Pr}({\chi }^2(d)\ge d+t)\le \text{Pr}(N>z(t)),t>0,$$ (32)

where N is a standard normal random variable and $z(t)=\sqrt{t-d\text{log}(1+\frac{t}{d})}$. Lemma 3 follows directly from Eq. (32) and inequality $\text{Pr}(N\ge z(t))\le \text{exp}(-\frac{z{(t)}^2}{2})$.

Proof of Theorem 2

Proof. Since (P̂, Q̂) is an optimal solution of Eq. (2), the following holds for any P and Q:

$$\sum _{i=1}^m\frac{1}{\mathit{\text{mn}}}{\Vert X_i^T({\widehat{\mathbf{\text{p}}}}_i+{\widehat{\mathbf{\text{q}}}}_i)-{\mathbf{\text{y}}}_i\Vert }^2\le \sum _{i=1}^m\frac{1}{\mathit{\text{mn}}}{\Vert X_i^T({\mathbf{\text{p}}}_i+{\mathbf{\text{q}}}_i)-{\mathbf{\text{y}}}_i\Vert }^2+{\lambda }_1({\Vert P\Vert }_{1,2}-{\Vert \widehat{P}\Vert }_{1,2})+{\lambda }_2({\Vert Q^T\Vert }_{1,2}-{\Vert {\widehat{Q}}^T\Vert }_{1,2}).$$

Substituting Eq. (14) into the above inequality, we have

$$\sum _{i=1}^m\frac{1}{\mathit{\text{mn}}}{\Vert X_i^T({\widehat{\mathbf{\text{p}}}}_i+{\widehat{\mathbf{\text{q}}}}_i)-{\mathbf{\text{f}}}_i^{\ast }\Vert }^2\le \sum _{i=1}^m\frac{1}{\mathit{\text{mn}}}{\Vert X_i^T({\mathbf{\text{p}}}_i+{\mathbf{\text{q}}}_i)-{\mathbf{\text{f}}}_i^{\ast }\Vert }^2+{\lambda }_1({\Vert P\Vert }_{1,2}-{\Vert \widehat{P}\Vert }_{1,2})+{\lambda }_2({\Vert Q^T\Vert }_{1,2}-{\Vert {\widehat{Q}}^T\Vert }_{1,2})+\frac{2}{\mathit{\text{mn}}}\langle Z,\widehat{P}-P\rangle +\frac{2}{\mathit{\text{mn}}}\langle Z,\widehat{Q}-Q\rangle ,$$ (33)

where Z = [X₁δ₁, ⋯,X_mδ_m] ∈ ℝ^{d × m} with its (j,i)-th entry given by

$$z_{\mathit{\text{ji}}}={\mathbf{\text{x}}}_j^{(i)}{\mathit{\delta }}_i=\sum _{k=1}^n{x}_{\mathit{\text{jk}}}^{(i)}{\delta }_{\mathit{\text{ki}}},i\in {\mathbb{N}}_m,j\in {\mathbb{N}}_d,$$ (34)

and $x_{\mathit{\text{jk}}}^{(i)}$ denotes the (j, k)-th entry of data matrix X_i for the i-th task. It follows from Eq. (1) that

$${\upsilon }_{\mathit{\text{ji}}}=\frac{1}{\sigma }{z}_{\mathit{\text{ji}}}=\frac{1}{\sigma }\sum _{k=1}^n{x}_{\mathit{\text{jk}}}^{(i)}{\delta }_{\mathit{\text{ki}}}(i\in {\mathbb{N}}_m,j\in {\mathbb{N}}_d)$$ (35)

are i.i.d. standard normal random variables (see Lemma 2), i.e., υ_ji ∼ N(0,1). Thus,

$$u=\sum _{j=1}^d\sum _{i=1}^m{\upsilon }_{\mathit{\text{ji}}}^2=\frac{1}{{\sigma }^2}{\Vert Z\Vert }_F^2$$

is a chi-squared random variable with dm degrees of freedom, and it follows from Lemma 3:

$$\text{Pr}(\frac{2}{\mathit{\text{mn}}}{\Vert Z\Vert }_F\ge \alpha )=\text{Pr}(u\ge \frac{{\alpha }^2{n}^2{m}^2}{4})\le \text{exp}(-\frac{1}{2}(t-\mathit{\text{dm}}\text{log}(1+\frac{t}{\mathit{\text{dm}}})\left)\right)(t>0),$$

which is equivalent to the following:

$$\text{Pr}(\frac{2}{\mathit{\text{mn}}}{\Vert Z\Vert }_F\le \alpha )\ge 1-\text{exp}(-\frac{1}{2}(t-\mathit{\text{dm}}\text{log}(1+\frac{t}{\mathit{\text{dm}}})\left)\right).$$ (36)

Under the event in Eq. (36), we bound $\frac{2}{\mathit{\text{mn}}}\langle Z,\widehat{P}-P\rangle$ as

$$\frac{2}{\mathit{\text{mn}}}\langle Z,\widehat{P}-P\rangle \le \frac{2}{\mathit{\text{mn}}}{\Vert Z\Vert }_F{\Vert \widehat{P}-P\Vert }_F\le \alpha {\Vert \widehat{P}-P\Vert }_F\le \alpha {\Vert \widehat{P}-P\Vert }_{1,2}.$$ (37)

Similarly, under the event in Eq. (36), we have

$$\frac{2}{\mathit{\text{mn}}}\langle Z,\widehat{Q}-Q\rangle \le \frac{2}{\mathit{\text{mn}}}{\Vert Z\Vert }_F{\Vert \widehat{Q}-Q\Vert }_F\le \alpha {\Vert \widehat{Q}-Q\Vert }_F\le \alpha {\Vert {\widehat{Q}}^T-Q^T\Vert }_{1,2}.$$ (38)

Combine Eq. (33), Eq. (37), Eq. (38) and Lemma 1, we verify Theorem 2.

Proof of Theorem 3

Proof. Let Γ_P = P̂ − P, Γ_Q = Q̂ − Q. Setting P = P*, Q = Q*, P* and Q* are the true weight matrices in Eq. (10), we have X^T vec(P + Q) = X^T vec(P* + Q*) = vec(F*). Following Eq. (18), we obtain

$$\frac{1}{\mathit{\text{mn}}}{\Vert X^T\text{vec}(\widehat{P}+\widehat{Q})-\text{vec}(F\ast )\Vert }^2\le 2{\lambda }_1{\Vert {(\widehat{P}-P\ast )}^{\mathcal{\text{J}}(P\ast )}\Vert }_{1,2}+2{\lambda }_2{\Vert {({\widehat{Q}}^T-Q{\ast }^T)}^{\mathcal{\text{J}}(Q{\ast }^T)}\Vert }_{1,2}.$$ (39)

Under Assumption 1, we have

$${\Vert {(\widehat{P}-P\ast )}^{\mathcal{\text{J}}(P\ast )}\Vert }_{1,2}\le \sqrt{r}{\Vert {(\widehat{P}-P\ast )}^{\mathcal{\text{J}}(P\ast )}\Vert }_F\le \frac{\sqrt{r}}{{\kappa }_1(r)\sqrt{\mathit{\text{mn}}}}\Vert X^T\text{vec}(\widehat{P}+\widehat{Q})-\text{vec}(F\ast )\Vert ,$$ (40)

$${\Vert {({\widehat{Q}}^T-Q{\ast }^T)}^{\mathcal{\text{J}}(Q{\ast }^T)}\Vert }_{1,2}\le \sqrt{c}{\Vert {({\widehat{Q}}^T-Q{\ast }^T)}^{\mathcal{\text{J}}(Q{\ast }^T)}\Vert }_F\le \frac{\sqrt{c}}{{\kappa }_2(c)\sqrt{\mathit{\text{mn}}}}\Vert X^T\text{vec}(\widehat{P}+\widehat{Q})-\text{vec}(F\ast )\Vert .$$ (41)

Substituting Eq. (40) and Eq. (41) into Eq. (39), we obtain

$$\Vert X^T\text{vec}(\widehat{P}+\widehat{Q})-\text{vec}(F\ast )\Vert \le \sqrt{\mathit{\text{mn}}}(\frac{2{\lambda }_1\sqrt{r}}{{\kappa }_1(r)}+\frac{2{\lambda }_2\sqrt{c}}{{\kappa }_2(c)}),$$

which directly leads to Eq. (21).

Following Assumption 1, we have

$$\begin{array}{c}{\Vert {({\Gamma }_P)}^{\mathcal{\text{J}}\perp (P\ast )}\Vert }_{1,2}\le {\beta }_1{\Vert {({\Gamma }_P)}^{\mathcal{\text{J}}(P\ast )}\Vert }_{1,2},\\ {\Vert {({\Gamma }_Q^T)}^{\mathcal{\text{J}}\perp (Q{\ast }^T)}\Vert }_{1,2}\le {\beta }_2{\Vert {({\Gamma }_Q^T)}^{\mathcal{\text{J}}(Q{\ast }^T)}\Vert }_{1,2},\end{array}$$

which imply that

$${\Vert \widehat{P}-P\ast \Vert }_{1,2}\le ({\beta }_1+1){\Vert {(\widehat{P}-P\ast )}^{\mathcal{\text{J}}(P\ast )}\Vert }_{1,2},$$ (42)

$${\Vert {\widehat{Q}}^T-Q{\ast }^T\Vert }_{1,2}\le ({\beta }_2+1){\Vert {({\widehat{Q}}^T-Q{\ast }^T)}^{\mathcal{\text{J}}(Q{\ast }^T)}\Vert }_{1,2}.$$ (43)

Substituting Eq. (42) and Eq. (43)) into Eq. (40) and Eq. (41), and considering Eq. (21), we can easily verify Eq. (22) and Eq. (23).

To prove Eq. (28), we need to show the following two:

$$(a)\forall j\in {\widehat{\mathcal{\text{J}}}}_1\Rightarrow j\in \mathcal{\text{J}}(P\ast ),$$ (44)

$$(b)\forall j\in \mathcal{\text{J}}(P\ast )\Rightarrow j\in {\widehat{\mathcal{\text{J}}}}_1.$$ (45)

We first prove (a) by contradiction. Assume there exists a j₁ such that $j_1\in {\widehat{\mathcal{\text{J}}}}_1,j_1\notin \mathcal{\text{J}}(P\ast )$. Then according to the definitions of ${\widehat{\mathcal{\text{J}}}}_1$ and 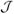(P*), we have

$$\Vert {\widehat{\mathbf{\text{p}}}}^{j_1}-{(\mathbf{\text{p}}\ast )}^{j_1}\Vert =\Vert {\widehat{\mathbf{\text{p}}}}^{j_1}\Vert >\frac{({\beta }_1+1)\sqrt{r}}{{\kappa }_1(r)}(\frac{2{\lambda }_1\sqrt{r}}{{\kappa }_1(r)}+\frac{2{\lambda }_2\sqrt{c}}{{\kappa }_2(c)}),$$

which contradicts with the following fact:

$${\Vert \widehat{P}-P\ast \Vert }_{\infty ,2}\le {\Vert \widehat{P}-P^{\ast }\Vert }_{1,2}\le \frac{({\beta }_1+1)\sqrt{r}}{{\kappa }_1(r)}(\frac{2{\lambda }_1\sqrt{r}}{{\kappa }_1(r)}+\frac{2{\lambda }_2\sqrt{c}}{{\kappa }_2(c)}).$$ (46)

We thus verify (a). Similarly, if we assume there exists a j₂ such that $j_2\in \mathcal{\text{J}}(P\ast ),j_2\notin {\widehat{\mathcal{\text{J}}}}_1$, then using the condition in Eq. (24) and the definition of ${\widehat{\mathcal{\text{J}}}}_1$ in Eq. (26), we have

$$\Vert {\widehat{\mathbf{\text{p}}}}^{j_2}-{(\mathbf{\text{p}}\ast )}^{j_2}\Vert \ge \Vert {(\mathbf{\text{p}}\ast )}^{j_2}\Vert -\Vert {\widehat{\mathbf{\text{p}}}}^{j_2}\Vert >\frac{({\beta }_1+1)\sqrt{r}}{{\kappa }_1(r)}(\frac{2{\lambda }_1\sqrt{r}}{{\kappa }_1(r)}+\frac{2{\lambda }_2\sqrt{c}}{{\kappa }_2(c)}),$$

which contradicts with Eq. (46), thus (b) holds. Combining (a) and (b), we verify Eq. (28). Similarly, we can prove Eq. (29).□