Abstract
Psychological scientists use statistical information to determine the workings of fellow humans. We argue so do young children. In a few years, children progress from viewing human actions as intentional and goal-directed to reasoning about the psychological causes underlying such actions. Here we show that preschoolers and 20-month-old infants can use statistical information – namely, a violation of random sampling – to infer that an agent is expressing a preference for one object over another. Children saw a person remove 5 items of one type from a container of objects. Preschoolers and infants only inferred a preference for that type of object when there was a mismatch between the sample and population. Mere outcome consistency, time spent with and positive attention toward the objects did not lead children to infer a preference. The findings provide an important demonstration of how statistical learning could underpin the rapid acquisition of early psychological knowledge.
Young children are avid psychologists. Within the first few years of life, children come to understand the actions of other people in terms of underlying psychological causes: desires, preferences, beliefs, emotions, knowledge states. It remains unclear, however, how children learn about these internal motivations. Perhaps, like psychological scientists, children use statistical evidence to reveal the nature of mind and action. Indeed, children are surrounded by statistical evidence for psychological causality; people’s behaviors are often regular, consistent, and contingent on particular contexts. Young children’s intuitive statistical abilities have been examined in physical reasoning (Teglas, Girotto, Gonzalez, & Bonatti, 2007; Xu & Garcia, 2008); word and scene segmentation (Saffran, Aslin, & Newport, 1996; Kirkham, Slemmer, & Johnson, 2002), language learning (Lany, Gómez, & Gerken, 2007; Xu & Tenenbaum, 2007a, 2007b), and causal reasoning (Schulz, Bonawitz, & Griffiths, 2007; Kushnir & Gopnik, 2005;2007). Here, we investigate whether young children use the statistical properties of human actions to learn about a psychological cause.
What may constitute the right kind of statistical evidence for a psychological cause? Most generally, psychologically caused actions are statistically non-random. Put another way, humans acting intentionally - in accord with their own internal motivations - have the ability to dramatically change statistical sequences of events. Recognizing when actions are non-random helps children learn about physical causal relations (see Gopnik et al, 2004). Recognizing when actions are non-random could similarly allow children to learn about the psychological states of intentional agents. A demonstration of this ability would inform us both about the scope of children’s attention to statistical information and their learning of naive psychology.
Consider an action which we would expect to be statistically random – a person taking toys out of a toy box with eyes closed. Not only adults but preschoolers (Denison, Konopczynski, Garcia, & Xu, 2006) and even infants (Teglas et al, 2007; Xu & Garcia, 2008) expect randomly drawn samples to be representative of underlying populations, and vise versa. For example, Xu & Garcia (2008; Xu & Denison, 2009) showed 8- and 11-month-old infants a person sampling 4 red balls and 1 white ball out of a box with eyes closed. When the contents of the box were revealed, infants looked longer at an unexpected population (a box full of mostly white balls with some red) than an expected population (mostly red balls and some white). However, when 11-month-olds saw a person with an explicitly expressed preference draw the sample intentionally (i.e. eyes open, looking in the box), Xu & Denison (2009) found that they did not form expectations about the contents of the box. Thus, 11-month-olds only seem to make random sampling assumptions about random, not intentional, actions.
These data leave open two intriguing possibilities. On the one hand, intentional actions might be a signal to children that statistical evidence is no longer relevant. Young children might instead learn about psychological causes by attending solely to psychological cues - eye gaze, reaching, facial expressions, affect, verbalizations -without regard to the statistical regularity/irregularity of those cues. On the other hand, violations of statistical regularity could themselves signal to young children the presence of a psychological cause, and also might help them to discern what that cause could be.
To address these issues, we examined children’s reasoning in a scenario where violations of random sampling provide a meaningful psychological cue by revealing a person’s preference. Imagine a person sampling five rubber frogs out of a toy box and playing happily with them. Does the intentional act itself – rather than its statistical properties – provide evidence of a preference for frogs? If most or all of the toys in the box are rubber frogs, the statistical information is in keeping with random draws from the box, providing no evidence that the person prefers rubber frogs to, let’s say, rubber ducks. If, however, the box is full of rubber ducks with very few frogs in it, then the sample of 5 frogs is not likely to have been drawn by chance. More likely, the person chose to take only frogs and so is displaying a preference for rubber frogs over rubber ducks. Importantly, in this example, psychological cues (gaze, reach, affect) are insufficient evidence to infer a preference. Generally, preferences, unlike momentary desires, require attending to the options not chosen – such as the other objects in the box. To learn about someone’s preference in this manner, therefore, requires that children attend to the violation of random sampling and use that statistical evidence to draw psychological conclusions.
In Experiment 1 we ask whether preschool children, who already have a general notion of preferences, can learn about a particular agent’s preference from an intentional action that violates random sampling. In Experiment 2 we ask whether statistical evidence plays a role in the emergence of a notion of preferences by extending our findings to 19- to 24-month old infants.
Experiment 1
In Experiment 1, an agent intentionally sampled 5 toys of the same type from a box of toys. We manipulated the population across three groups of preschoolers. In one group, 18% of the toys were of the selected type and 82% were another type. In the second group, 50% were of the selected type. In the final group, 100% were of the selected type. Later children were asked which object (the selected type, the alternative, or a third novel object) the agent preferred. Importantly, psychological cues to preference (such as positive affect) were identical across groups. Thus, if children infer preferences from psychological cues alone the groups should not differ. However, if children regard a violation of random sampling as a cue to preference, then they should infer preference most strongly in the 18% group, least in the 100% group, and the 50% group should fall somewhere in between.
Method
Participants
Seventy-two preschoolers participated, 36 3-year-olds (M=44.1 months, SD=3.2 months) and 36 4-year-olds (M=53.9 months, SD=3.3 months). Participants were recruited from local preschools in a small, Midwestern city and were predominantly non-Hispanic white and middle-class. Children were randomly assigned to the18%, 50%, or 100% conditions. The average age (M=49.1 months overall, SD=5.9 months) was comparable across conditions (F(2,68) = 1.56, ns).
Materials
Two sets of toys (with three types per set) were used. In each set, one type of toy was the target chosen by the agent. A second type was in the box in the 50% and 18% conditions. A third type was never in the box but provided a novelty control (see below). Set 1 contained foam shapes – red circles and blue flowers alternated as the target and yellow tubes were always the novel object. Set 2 contained small balls – soft replica baseballs and soft replica basketballs alternated as the target and green practice golf balls were the novel object. From each set of materials, we created boxes to serve as the “populations”. Boxes were black, 13” × 5” × 6”, and opaque. Four 18% boxes contained a 7:31 ratio of target to other object (e.g. 7 red circles and 31 blue flowers). Two 50% boxes contained a 19:19 ratio of target to other object (e.g. 19 red circles and19 blue flowers). Four 100% boxes contained 38 target toys (e.g. 38 red circles). An additional set of 5 toys of each type were kept in 3 separate bowls to be used for the preference question at the end of the procedure. Figure 1 depicts the materials and procedure for an example trial.
Figure 1.
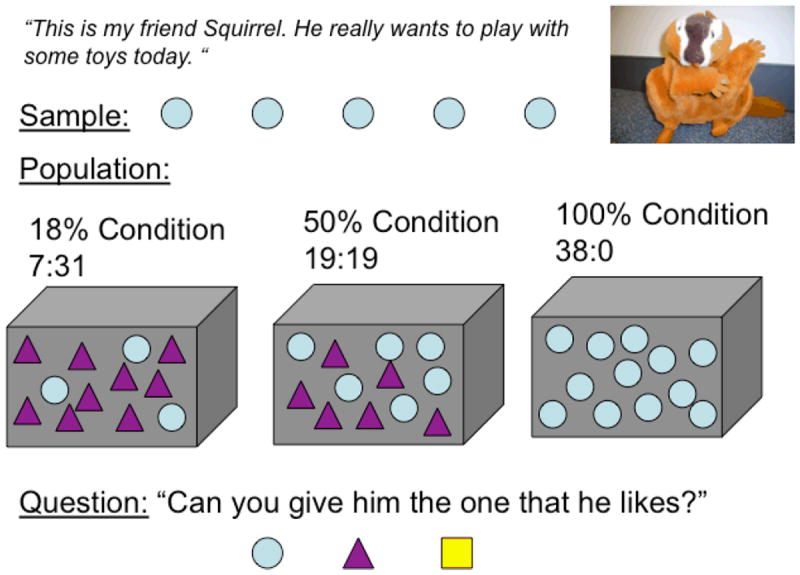
A schematic illustration of the procedure for Experiment 1. The sample was always 5 objects of the same type (here shown as circles, but see procedure for description of actual items used). The population varied between subjects (18% circles, 50% circles, or 100% circles). Children chose an object to give to Squirrel out of one of 3 bowls: a bowl of 5 target items, 5 alternate items, or 5 novel items.
Procedure
Each child sat individually at a table opposite the experimenter who began by introducing the agent (a puppet named “Squirrel”) to the child. Children were told that Squirrel liked some toys but not others. The experimenter removed Squirrel and placed three bowls of toys from the first set out on the table. She asked the child to label them, and if the child could not identify objects labels were provided.
The experimenter then removed the bowls and took out the first box. She opened the top so the child could look at the objects. She prompted the child to label objects and, importantly, made no reference to the quantity or proportion of the objects. The experimenter then brought Squirrel out again and asked if he wanted to take some toys to play with. Squirrel removed a sample of 5 target objects one at a time, placing them on the table in a pile. After the 5th item, the experimenter closed the box and Squirrel played with the toys then left again. The amount of time spent selecting and playing with the toys was kept equal across the conditions. The experimenter put the box away, set out the 3 bowls, then brought Squirrel out again and said, “Squirrel is back! He wants some toys again. Can you give him the ones that he likes?” The child’s first choice was recorded.
The procedure was repeated with the other set of objects. The proportion of objects in the box varied between subjects, but not between trials. The set of toys presented first (foam shapes or balls) was counterbalanced across subjects. The sample drawn from the box was counterbalanced along with the box contents. Order of placement of the bowls (left, right, center) was also counterbalanced.
Results and Discussion
The average number of targets chosen (out of 2) is shown in Figure 2. The results reveal that children used the statistical cue - the violation of random sampling - to infer that Squirrel was selecting objects based on a preference. A 2 (age: 3, 4) × 3 (condition: 18%, 50%, 100%) ANOVA revealed a main effect for condition (F(2,66)=4.34, p=.017, r2=.12) and no other significant effects. As predicted, children chose the target object most in the 18% condition (M=1.63, SE=0.15), least in the 100% condition (M=1.00, SE=0.15), and the 50% condition fell in between (M=1.31, SE = 0.16), yielding a significant linear trend (p=.004). Directional (one-tailed) t-tests showed that the 18% group was significantly more likely to pick the target than the 50% group (t(46)=1.72; p=.045, d=.48) and the 50% group was marginally more likely to pick the target than the100% group (t(46)=1.3; p=.096, d=.41). The difference between the two extremes (18% versus 100%) was significant (t(46)=3.16; p=.002, d=.89).
Figure 2.

The average number of times children chose to give Squirrel the target (sampled) object across the three conditions. The error bars represent 95% confidence intervals around the mean.
We also tallied the number of children who gave Squirrel the target toy on both trials in order to compare responses to chance. In the 18% condition, 16/24 children (67%) gave the Squirrel the target object on both trials. In the 50% condition, 11/24 children (46%), and in the 100% condition only 7/24 children (28%) chose the target object on both trials. Responses in the 18% condition were significantly above chance (Binomial test, p<.001) and significantly different from the 100% condition (Fischer’s exact test, p=.037). Responses in the 50% condition was also above chance (Binomial test, p=.001). However, responses in the 100% condition were not different from chance (Binomial test, ns). This analysis supports the conclusion that the violation of random sampling, rather than the psychological and linguistic cues, accounted for children’s inference that Squirrel had chosen the target because he preferred it.
Conceivably, children might have selected the target more often in the 18% and 50% conditions, not because they inferred that Squirrel had a preference for the target, but because they thought he was avoiding the other object in the box. An analysis of children’s alternative responses reveals that this was not the case. On trials where children did not give Squirrel the target toy, responses were roughly equally distributed between the alternate toy in the box and the novel toy which was not in the box (50%: 7 novel toy picks, 10 alternate toy picks; 18%: 5 novel toy picks, 4 alternate toy picks; 100%: 16 novel toy picks, 8 alternate toy picks). This suggests that children were basing their response on preference, rather than avoidance.
Experiment 2
Experiment 1 demonstrated that preschoolers can use statistical evidence in the form of a violation of random sampling to infer a psychological cause – a preference. Is such reasoning a result of or potentially a contributor to children’s emerging understanding of preference? It is generally thought that infants first infer desires and preferences by appealing to emotional cues, such as pleasure and disgust (Repacholi & Gopnik, 1997). Yet, in the case of non-social events, intuitive sampling assumptions may be present in infancy. Can infants, like preschoolers, use statistical sampling information to infer preferences, even when emotional cues are controlled for?
In Experiment 2, we presented older infants (average age, 20 months) with a scenario similar to Experiment 1. We concentrate on older infants because previous research shows that infants understand the link between emotional reactions and desires at this age. We also refined and simplified the procedure in several fashions. The agent was changed from a puppet to a live person, in part because the actions of human agents are easier for infants to interpret as intentional (e.g. Woodward 1998) and also because a live actor can provide real emotional cues signaling desire. We made the procedure less verbal (removing the word “likes” throughout) and less taxing on memory (by making the boxes clear so infants could see the proportions throughout). Infant judgments were elicited by having them give an object to the agent. Previous research has shown that infants can interpret an adult’s enthusiastic but ambiguous requests as a request for desired objects (Tomasello & Haberl, 2003).
Infants saw a person select 5 items of one type out of a box containing a minority of that type (18%) or a majority of that type (82%). Since both boxes contained both types of toy, any differences between conditions could not be artificially strengthened by novelty effects. Again, psychological/emotional cues to preference were present, but were identical across groups. Thus, if infants infer preferences from a violation of random sampling, they should do so only when the sample is non-representative – in the 18% but not the 82% condition.
Method
Participants
Participants were 48 infants (M=20.23 months, Range = 19-24 months) recruited from a baby registry in a small Midwestern city. Twenty-four infants were assigned to the 18% condition, and 24 to the 82% condition. Mean ages were equivalent in each condition (t(46)=.589, ns).1
Materials
The toys were yellow rubber ducks or green rubber frogs of equal size (2 inches in diameter) placed in clear plastic boxes of 7 3/8”×6 5/8”×4 3/4”. One box contained a 7:31 ratio of ducks to frogs, and the other contained a 31:7 ratio. An additional set of 5 toys of each type were kept in 2 separate bowls to be used for the preference question at the end of the procedure (see below).
Procedure
Infants sat in a high-chair at a table in a laboratory room with the experimenter seated to the infant’s left. The infant’s parent sat in a separate chair behind and to the right of their child. The infant was allowed 2 minutes to play with the bowls of frogs and ducks. Then the bowls were removed and the confederate entered. The experimenter introduced the confederate by name and said “let’s play!”
The confederate sat opposite the infant at the table. The infant, experimenter, confederate began by playing a turn-taking game with a toy car, a cup, and a ball. This allowed the infant to become comfortable sharing with the confederate. After this the confederate left the room.
The experimenter put the box of toys on the table. She opened the box, labeled the toys, and let the child handle them for a few seconds before calling the confederate to play. The confederate returned to her seat across from the infant and removed 5 toys (all ducks or frogs) out of the box one at a time. While pulling out each toy she smiled and vocalized positively, alternating between labeling the toy (i.e. “wow, frogs!) and making the sound of the animal (i.e. “Ribit ribit!”). She played with the toys for the remaining time (30 seconds total) then left the room.
The experimenter put the box away and put the 2 bowls of toys on a tray out of reach so the infant couldn’t touch the objects before response coding began. The confederate returned and stood on a floor mark slightly away from the table, centered between the two bowls. She held out her hand palm up (centered) looked directly at the child and said “Oh goody! Just what I wanted! Can you give me one?” The experimenter slid the tray toward the infant and coding of the response began.
Each infant participated in one trial. The object designated the target was counterbalanced (ducks vs frogs) and either in the minority or the majority (18% vs 82%). Order of placement of the bowls (left, right) was also counterbalanced.
Coding
The infant’s behavior right after the confederate’s question was coded for the first object (or objects) the infant touched (“first touch”) and the first object (or objects) that s/he handed over (“first offer”). A subset of the data (20% from each condition) was coded by a second researcher. Agreement was 100%.
Results and Discussion
Consistent with the findings from Experiment 1, when the sample was drawn from the minority (18%) but not the majority (82%) of toys in the box, infants were more likely to infer that the confederate had a preference. Table 1 shows infants’ responses. Infants’ first touches reveal a significant difference between conditions (χ2 (2, 48)=6.89; p=.032, φ=.38). Infants first offers do not significantly differ across conditions χ2 (2, 48)=3.48; ns). To reconcile this difference and create a fuller picture of infants’ responding, we created a composite code combining first touches and first offers, also shown in Table 1. In the 18% condition 14/24 infants (58%) touched and offered the target to the confederate. The remaining 10 infants (42%) touched and offered the alternate object. In the 82% condition, only 5/24 infants (21%) touched and offered the target to the confederate, and 13 (54%) touched and offered the alternate object. Of the remaining 6 infants in the 82% condition, 4 (17%) touched the alternate then switched their response to offer the target, which indicates that they considered both objects in their responding, (as in studies that examine sequential touching – for example, Oakes & Madole, 2000), and 2 (8%) touched and offered both objects simultaneously. The difference in composite responses between conditions is significant (χ2 (3, 48)=10.65; p=.014, φ=.47). A comparison of infants who first touched and first offered the target between conditions is also significant, (14 vs. 5; Fischer’s exact tests, p=.017). Thus, when there was a violation of random sampling, 19-24 month-old infants’ first touch alone and in combination with their first offer favored the target object. On the other hand, with no violation of random sampling (no statistical cues for preference) it was difficult for infants to interpret the confederates’ request, resulting in more variable responding (including sequential touching) and a tendency to favor the alternate, more novel, object.
Table 1.
The results of Experiment 2 in two parts. Part 1 shows infants’ first touches and first offers across both conditions. Part 2 shows the composite coding (combining touches and offers) across both conditions. This creates 4 mutually exclusive categories, shown below.
| Part 1 – Separate Responses | 18% Condition (Sampling Violation) | 82% Condition (No Sampling Violation) | ||
|---|---|---|---|---|
| First Touch | First Offer | First Touch | First Offer | |
| Target | 13 | 14 | 5 | 9 |
| Alternate | 10 | 10 | 14 | 13 |
| Both | 1 | 0 | 5 | 2 |
| Part 2 – Combined Responses1 | 18% Condition (Sampling Violation) | 82% Condition (No Sampling Violation) |
|
| ||
| Category 1: Touch and Offer Target | 14 | 5 |
| Category 2: Touch and Offer Alternate | 10 | 13 |
| Category 3: Touch Alternate and Switch to Offer Target | 0 | 4 |
| Category 4: Touch and Offer Both | 0 | 2 |
Four children (1 in the 18% condition and 3 in the 82% condition) who first touched both objects together but then offered only one were coded as category 1 or 2.
Since both boxes contained two types of toys, these results were not due to simply associating the agent’s selection of one of type of toy with her preference, and in both conditions the confederate played excitedly with her choices so results were not based solely on the confederate’s social-emotional reactions. Instead, the infants encoded the proportion of the two types of toys in each box, and in the case of a violation of random sampling they inferred a preference for that type of toy.
General Discussion
These studies provide the first evidence that young children can use intuitive statistical abilities to infer a psychological cause - a preference. In Experiment 1, preschoolers inferred the preferences of an agent when the sample drawn violated random sampling. Additionally, the less representative the sample, the more likely children were to infer a preference. In Experiment 2, we extended this finding to 20-month-old infants.
We argue that children’s inferences were based on sensitivity to statistical sampling, and not based solely on outcome consistency or affective cues, because the only difference between conditions was the proportion of alternate items in the box which were not sampled. Our results thus argue against a simple associative learning mechanism (i.e., if a puppet or person selects/is associated with one type of object, then he/she must prefer it over other types of objects). Instead, these results are consistent with a statistical inference mechanism where young children noted the representativeness of a sample relative to a larger population, and used non-random sampling as the basis for their inference. With preschoolers, the evidence also suggests that the degree of non-representativeness was correlated with the strength of their inference about preferences, a clear sign of employing a probabilistic reasoning strategy. Our results support the intriguing conclusion that statistical inference plays a critical role in early social learning – both as infants form initial notions of psychological causality and later as preschoolers achieve more detailed and sophisticated psychological knowledge. Thus, this initial demonstration sets the stage for future research. Important questions remain about how affective, behavioral, and statistical cues combine in children’s social learning. In infants, is the initial construal of actions as intentional and goal directed (Gergely & Csibra, 2003; Phillips & Wellman, 2005; Sommerville, & Crane, 2009; Woodward, 1998; 2009) a sufficient starting point? In older children, could statistical evidence enable children to transition from understanding preferences to reasoning about stable personality traits (Heyman & Gelman, 2000; Kalish, 2002)? Even in advance of further research, our data demonstrate that statistical information dovetails along with information about intentional-emotional properties of human action, to shape children’s early learning about the social world.
Acknowledgments
This research was supported by the McDonnell Collaborative Initiative on Causal Learning, grant HD-22149 from NICHD, and an NICHD post-doctoral fellowship to T.K.
Footnotes
Twelve more children (4 in the 18% condition, 8 in the 82% condition) were tested who touched, but refused to hand over, any objects. An analysis of all of the “first touch” data including these infants results in a statistically significant difference between the 18% and 82% groups (χ2 (2, 60)=6.16, P<.05).
References
- Denison S, Konopczynski K, Garcia V, Xu F. Probabilistic reasoning in preschoolers: random sampling and base rate. In: Sun R, Miyake N, editors. Proceedings of the 28th Annual Conference of the Cognitive Science Society; 2006. pp. 1216–1221. [Google Scholar]
- Gergely G, Csibra G. Teleological reasoning in infancy: The naïve theory of rational action. Trends in Cognitive Sciences. 2003;7(7):287–292. doi: 10.1016/s1364-6613(03)00128-1. [DOI] [PubMed] [Google Scholar]
- Gopnik A, Glymour C, Sobel DM, Schulz LE, Kushnir T, Danks D. A theory of causal learning in children: Causal maps and Bayes nets. Psychological Review. 2004;111:1–30. doi: 10.1037/0033-295X.111.1.3. [DOI] [PubMed] [Google Scholar]
- Heyman G, Gelman S. Beliefs about the origins of human psychological traits. Developmental Psychology. 2000;36(5):663–678. doi: 10.1037/0012-1649.36.5.663. [DOI] [PubMed] [Google Scholar]
- Kalish C. Children’s predictions of consistency in people’s actions. Cognition. 2002;84(3):237–265. doi: 10.1016/s0010-0277(02)00052-5. [DOI] [PubMed] [Google Scholar]
- Kirkham N, Slemmer J, Johnson S. Visual statistical learning in infancy: Evidence for a domain general learning mechanism. Cognition. 2002;83(2):B35–b42. doi: 10.1016/s0010-0277(02)00004-5. [DOI] [PubMed] [Google Scholar]
- Kushnir T, Gopnik A. Children infer causal strength from probabilities and interventions. Psychological Science. 2005;16:678–683. doi: 10.1111/j.1467-9280.2005.01595.x. [DOI] [PubMed] [Google Scholar]
- Kushnir T, Gopnik A. Conditional probability versus spatial contiguity in causal learning: Preschoolers use new contingency evidence to overcome prior spatial assumptions. Developmental Psychology. 2007;44:186–196. doi: 10.1037/0012-1649.43.1.186. [DOI] [PubMed] [Google Scholar]
- Lany J, Gómez R, Gerken L. The role of prior experience in language acquisition. Cognitive Science: A Multidisciplinary Journal. 2007;31(3):481–507. doi: 10.1080/15326900701326584. [DOI] [PubMed] [Google Scholar]
- Phillips A, Wellman H. Infants’ understanding of object-directed action. Cognition. 2005;98(2):137–155. doi: 10.1016/j.cognition.2004.11.005. [DOI] [PubMed] [Google Scholar]
- Repacholi B, Gopnik A. Early reasoning about desires: Evidence from 14- and 18-month-olds. Developmental Psychology. 1997;33(1):12–21. doi: 10.1037//0012-1649.33.1.12. [DOI] [PubMed] [Google Scholar]
- Saffran J, Aslin R, Newport E. Statistical learning by 8-month-old infants. Science. 1996;274(5294):1926–1928. doi: 10.1126/science.274.5294.1926. [DOI] [PubMed] [Google Scholar]
- Schulz L, Bonawitz E, Griffiths T. Can being scared cause tummy aches? Naive theories, ambiguous evidence, and preschoolers’ causal inferences. Developmental Psychology. 2007;43(5):1124–1139. doi: 10.1037/0012-1649.43.5.1124. [DOI] [PubMed] [Google Scholar]
- Sommerville JA, Crane CC. Ten-month-old infants use prior information to identify an actor’s goal. Developmental Science. 2009;12:314–325. doi: 10.1111/j.1467-7687.2008.00787.x. [DOI] [PubMed] [Google Scholar]
- Téglás E, Girotto V, Gonzalez M, Bonatti L. Intuitions of probabilities shape expectations about the future at 12 months and beyond. Proceedings of the National Academy of Sciences of the United States of America. 2007;104(48):19156–19159. doi: 10.1073/pnas.0700271104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu F, Denison S. Statistical inference and sensitivity to sampling in 11-month-old infants. Cognition. 2009;112:107–114. doi: 10.1016/j.cognition.2009.04.006. [DOI] [PubMed] [Google Scholar]
- Xu F, Garcia V. Intuitive statistics by 8-month-old infants. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:5012–5015. doi: 10.1073/pnas.0704450105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu F, Tenenbaum J. Sensitivity to sampling in Bayesian word learning. Developmental Science. 2007a;10(3):288–297. doi: 10.1111/j.1467-7687.2007.00590.x. [DOI] [PubMed] [Google Scholar]
- Xu F, Tenenbaum J. Word learning as Bayesian inference. Psychological Review. 2007b;114(2):245–272. doi: 10.1037/0033-295X.114.2.245. [DOI] [PubMed] [Google Scholar]
- Wellman H, Phillips A, Dunphy-Lelii S, LaLonde N. Infant social attention predicts preschool social cognition. Developmental Science. 2004;7(3):283–288. doi: 10.1111/j.1467-7687.2004.00347.x. [DOI] [PubMed] [Google Scholar]
- Woodward A. Infants selectively encode the goal object of an actor’s reach. Cognition. 1998;69(1):1–34. doi: 10.1016/s0010-0277(98)00058-4. [DOI] [PubMed] [Google Scholar]
- Woodward A. Infants’ grasp of others’ intentions. Current Directions in Psychological Science. 2009;18(1):53–57. doi: 10.1111/j.1467-8721.2009.01605.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodward J. Making things happen: A theory of causal explanation. New York: Oxford; 2003. [Google Scholar]


