Fig. 4.

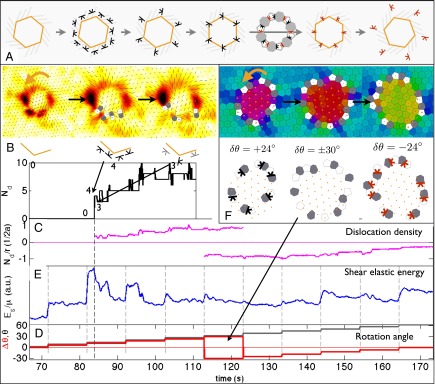
Topological defect dynamics in the formation and rotation of a grain. (See also Movies S8 and S9.) A commensurate set of traps was rotated counterclockwise from 0° to 60° in 6° steps (D, gray line), giving rise to a grain with boundary. A cartoon of the idealized process is shown in A. The initial response is an elastic pure-shear deformation (B) with a corresponding build-up in shear elastic energy 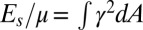(E). At a rotation angle of 12°, the shear stress makes defects unbind along the edges after a short delay (A and B), glide to relieve the stress (E, blue line), and react to form a grain boundary (A and B). Further unbindings, annihilations, and glide movements produce an oriented dislocation line density (C, purple line) along the grain boundary that mediates the difference in angle between the lattice and grain 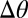(D, red line). As the rotation angle reaches 30° 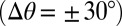, 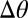reaches a maximum and becomes ambiguous in sign. The defect density reaches a corresponding maximum. Beyond 30°, 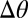becomes negative and the defect orientation must change from clockwise (black) to counterclockwise (red). If all defects along the boundary are in contact (the appropriate density to mediate a difference in orientation of 30°), simple disclination reassociation from clockwise to counterclockwise reverses the dislocations smoothly (A, step v). In the experiment we observe this mechanism along part of the boundary; however, in regions in which the defect density does not reach unity, the defects unbind into disclinations separated by a lattice constant (F) and these recombine with their counterparts from a neighboring dislocation. For further rotation, the dislocation line density is reduced as the defects are pushed outward.