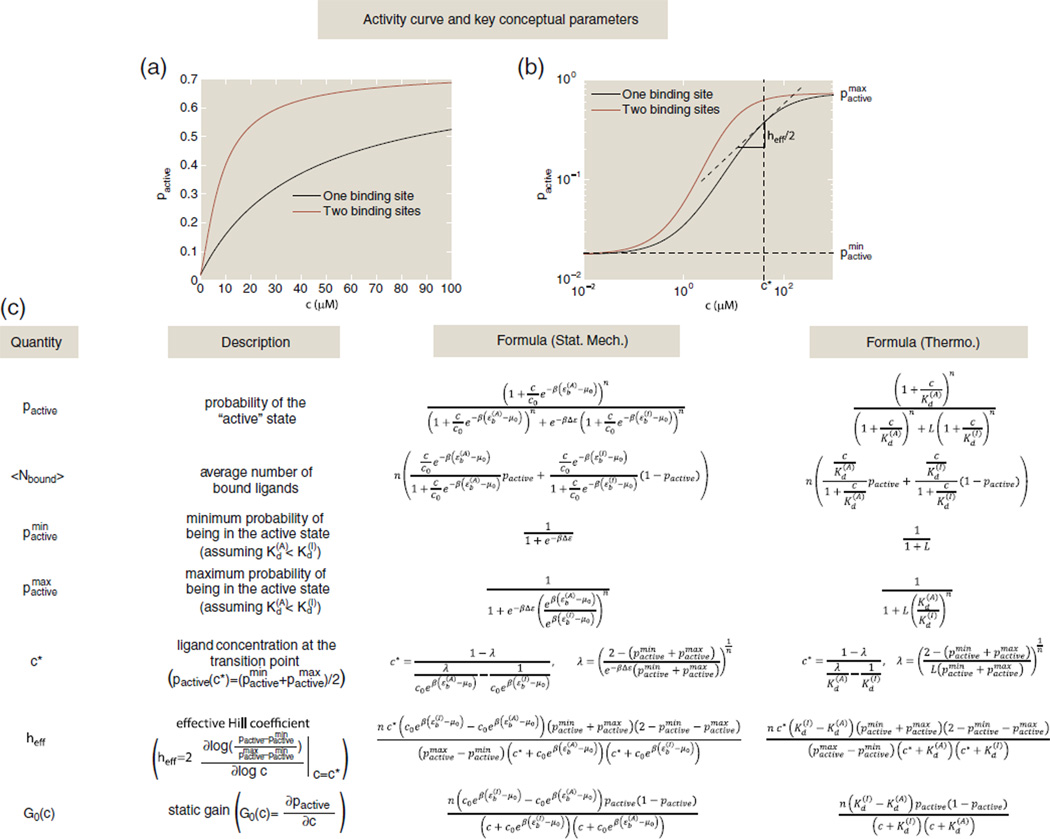
Fig. 2.

Table of key quantities that can be computed within the MWC framework. (a) The activity curve on a linear scale for two MWC molecules: a one-site receptor with Δε = ε_I − ε_A = −4 k_BT, $K_{\mathrm{d}}^{(\mathrm{A})}=1\mu \mathrm{M}$ and $K_{\mathrm{d}}^{(\mathrm{I})}=148\mu \mathrm{M}$, giving a difference in binding energy of ${\mathrm{\epsilon }}_{\mathrm{b}}^{(\mathrm{A})}-{\mathrm{\epsilon }}_{\mathrm{b}}^{(\mathrm{I})}=\text{log}\frac{K_{\mathrm{d}}^{(\mathrm{A})}}{K_{\mathrm{d}}^{(\mathrm{I})}}=-4k_{\mathrm{B}}T$; and a two-site receptor with Δε = ε_I − ε_A = −4 k_BT, $K_{\mathrm{d}}^{(\mathrm{A})}=1\mu \mathrm{M}$, and $K_{\mathrm{d}}^{(\mathrm{I})}=12.2\mu \mathrm{M}$, giving a binding energy difference of ${\mathrm{\epsilon }}_{\mathrm{b}}^{(\mathrm{A})}-{\mathrm{\epsilon }}_{\mathrm{b}}^{(\mathrm{I})}=\text{log}\frac{K_{\mathrm{d}}^{(\mathrm{A})}}{K_{\mathrm{d}}^{(\mathrm{I})}}=-2k_{\mathrm{B}}T$. (b) The activity curves from (a) with concentrations on a log scale. The transition point concentration c* = 40.6 µM and effective Hill coefficient h_eff = 1 are shown with vertical and horizontal lines, respectively, for the one-site receptor. (c) This table gives formulas for some of the key parameters of interest in both statistical mechanics and thermodynamic language. Here, n is the total number of binding sites on the receptor, L = e^−βΔε is the conformational equilibrium constant where Δε = ε_I − ε_A is the difference in conformational energy between the inactive and active state, $K_{\mathrm{d}}^{(\mathrm{I})}=c_0{e}^{\mathrm{\beta }({\mathrm{\epsilon }}_{\mathrm{b}}^{(\mathrm{I})}-{\mathrm{\mu }}_0)}$ is the inactive state's dissociation constant for ligand binding, $K_{\mathrm{d}}^{(\mathrm{A})}=c_0{e}^{\mathrm{\beta }({\mathrm{\epsilon }}_{\mathrm{b}}^{(\mathrm{A})}-{\mathrm{\mu }}_0)}$ is the active state's dissociation constant for ligand binding and c is the ligand concentration.