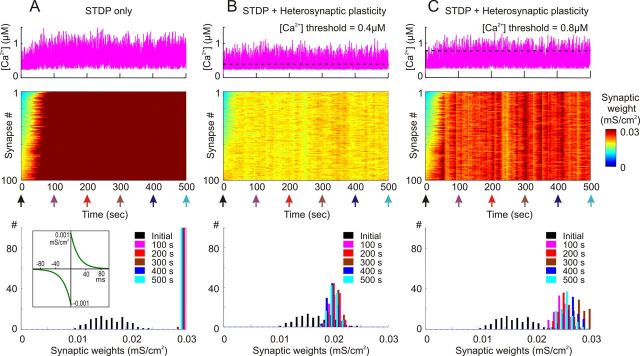
Figure 6.

Normalizing effect of heterosynaptic plasticity on synaptic weights is long lasting and operates over a range of calcium thresholds. A, Weakly correlated inputs express runaway dynamics and lasting saturation of synaptic weights in a model with symmetrical STDP. Simulation had the same parameters as in Figure 4A (100 presynaptic spike trains at average rate of 1 Hz; cross-correlation was 0.348 ± 0.05; symmetrical STDP rule τ⁺ = τ⁻ = 20 ms; a⁺ = a⁻ = 10⁻³ mS/cm²; bottom, inset), but was run over 500 s. Changes of intracellular [Ca²⁺] (top), changes of synaptic weights, color coded, with synapses sorted by their synaptic weights at the beginning of experiment (middle) and distributions of synaptic weights at the beginning of the experiment (black; 20 ms) and after 100, 200, 300, 400, and 500 s of simulation, as indicated (bottom). Note that STDP produced runaway dynamics of synaptic weights leading to their saturation. Once saturated after about 80 s, synaptic weights remained at the extreme (0.03 mS/cm²). B, C, Heterosynaptic plasticity prevents runaway dynamics of synaptic weights and leads to a lasting stabilization of synaptic weight distribution within an operation range. The same model as in A is used, but with the mechanism for heterosynaptic plasticity (as described in Fig. 3) with [Ca²⁺] threshold 0.4 μm (B) or 0.8 μm (C) added to each synapse. Calcium thresholds are shown as dashed lines over the plots of [Ca²⁺] change. Other conventions are as in A. Note that synaptic weights are not saturated, but remain normally distributed within the operation rage. Also note that the final distribution of synaptic weights depends on calcium threshold of heterosynaptic plasticity.