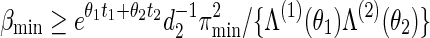Abstract
Monte Carlo methods can provide accurate p-value estimates of word counting test statistics and are easy to implement. They are especially attractive when an asymptotic theory is absent or when either the search sequence or the word pattern is too short for the application of asymptotic formulae. Naive direct Monte Carlo is undesirable for the estimation of small probabilities because the associated rare events of interest are seldom generated. We propose instead efficient importance sampling algorithms that use controlled insertion of the desired word patterns on randomly generated sequences. The implementation is illustrated on word patterns of biological interest: palindromes and inverted repeats, patterns arising from position-specific weight matrices (PSWMs), and co-occurrences of pairs of motifs.
Key words: importance sampling, Monte Carlo, motifs, palindromes, position-specific weight matrices
1. Introduction
Searching for matches to a word pattern, also called a motif, is an important task in computational biology. The word pattern usually represents a functional site, such as a transcription factor binding site (TFBS) in a promoter region of a DNA sequence or a ligand docking site in a protein sequence. Statistical significance of over-representation of these word patterns provides valuable clues to biologists. Consequently, much work has been done on the use of asymptotic limiting distributions to approximate these p-values (Prum et al., 1995; Reinert et al., 2000; Régnier, 2000; Robin et al., 2002; Huang et al., 2004; Leung et al., 2005; Mitrophanov and Borodovsky, 2006; Pape et al., 2008). However, the approximations may not be accurate for short words or for words consisting of repeats and most theoretical approximations work only in specific settings. String-based recursive methods can provide exact p-values (Gusfield, 1997), but they can be computationally expensive when the number of words in the word pattern is large.
Direct Monte Carlo algorithms for estimating p-values of word patterns are easy to implement but are inefficient for the estimation of very small p-values, because in such cases, almost all the simulated sequences do not contain the required number of word patterns. We propose in this article importance sampling algorithms that insert the desired word patterns, either randomly or controlled by a hidden Markov model, on the simulated sequences. The algorithms are described in Section 2 and are illustrated on several word patterns of biological interest: palindromes and inverted repeats in Section 3, high-scoring words with respect to position-specific weight matrices (PSWMs) in Section 4, and co-occurrences of motifs in Section 5. Numerical results show that variance reduction of several orders of magnitude are achieved when applying the proposed importance sampling algorithms on small p-values. The technical details are consolidated in Appendices A–D and include a proof of the asymptotic optimality of the importance sampling algorithms (see Appendix D).
2. Importance Sampling Of Word Patterns
2.1. Word counting
Let |B| denote the number of elements in a set B. By selecting randomly from a finite set B, we shall mean that each 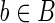 has probability |B|−1 of being selected. For any two sequences
has probability |B|−1 of being selected. For any two sequences 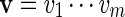 and
and 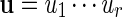 , the notation vu shall denote the concatenated sequence
, the notation vu shall denote the concatenated sequence 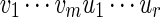 . We also denote the length of v by ℓ(v)( = m). Although we assume implicitly an alphabet χ = {a, c, g, t}, representing the four nucleotide bases of DNA sequences, the algorithms can be applied on any countable alphabet, for example the alphabet of 20 amino acids in protein sequences.
. We also denote the length of v by ℓ(v)( = m). Although we assume implicitly an alphabet χ = {a, c, g, t}, representing the four nucleotide bases of DNA sequences, the algorithms can be applied on any countable alphabet, for example the alphabet of 20 amino acids in protein sequences.
We will represent the word pattern of interest by a set of words 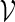 and assume that
and assume that 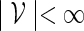 . Let
. Let 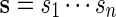 denote a sequence of DNA bases under investigation and let Nm be the maximum number of non-overlapping words from
denote a sequence of DNA bases under investigation and let Nm be the maximum number of non-overlapping words from 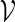 in
in 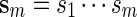 . We say that there exists a word in
. We say that there exists a word in 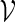 at the end of sm if
at the end of sm if 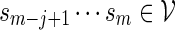 for some j > 0. Moreover, the smallest such j is the length of the shortest word at the end of sm. We have the recursive relations, for m ≥ 1,
for some j > 0. Moreover, the smallest such j is the length of the shortest word at the end of sm. We have the recursive relations, for m ≥ 1,
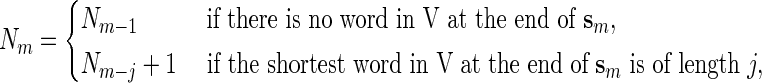 |
(2.1) |
with the initialization N0 = 0. We denote Nn simply by N. It is also possible to modify (2.1) to handle the counting of possibly overlapping words.
2.2. Monte Carlo evaluation of statistical significance
We begin by describing direct Monte Carlo. To evaluate the signifiance of observing c word patterns in an observed sequence s, we generate independent copies of the sequence from a Markov chain with transition probabilities estimated either from s or from a local neighborhood of s. The proportion of times {N ≥ c} occurs among the independent copies of s is then the direct Monte Carlo estimate of the p-value pc := P{N ≥ c}.
It is quite common for many sequences to be analyzed simultaneously. Hence to correct for the effect of multiple comparisons, a very small p-value is required for any one sequence before statistical significance can be concluded. Direct Monte Carlo is well-known to be very inefficient for estimating small probabilities in general and many importance sampling schemes have been proposed to overcome this drawback, for example, in sequential analysis (Siegmund, 1976), communication systems (Cottrell et al., 1983), bootstrapping (Johns, 1988; Do and Hall, 1992), signal detection (Lai and Shan, 1999), moderate deviations (Fuh and Hu, 2004), and scan statistics (Chan and Zhang, 2007). In this article, we provide change of measures that are effective for the importance sampling of word patterns.
For ease of exposition, assume that the background sequence of bases follows a first-order Markov chain with positive transition probabilities
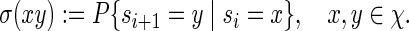 |
(2.2) |
Let π be the stationary distribution, and let 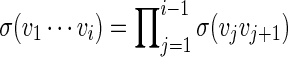 . Before executing the importance sampling algorithms, we first create a word bank of the desired word pattern, with each word in the word bank taking the value
. Before executing the importance sampling algorithms, we first create a word bank of the desired word pattern, with each word in the word bank taking the value 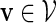 with probability q(v) > 0. The procedure for the selection of q and construction of the word banks will be elaborated in Sections 3–5. For completeness, we define q(v) = 0 when
with probability q(v) > 0. The procedure for the selection of q and construction of the word banks will be elaborated in Sections 3–5. For completeness, we define q(v) = 0 when 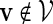 . Let β(v) = q(v)/σ(v). For ease of computation, we shall generate a dummy variable s0 before generating s and denote
. Let β(v) = q(v)/σ(v). For ease of computation, we shall generate a dummy variable s0 before generating s and denote 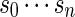 by s0. The first importance sampling algorithm, for the estimation of p1 only, is as follows.
by s0. The first importance sampling algorithm, for the estimation of p1 only, is as follows.
Algorithm A (forc = 1):
Select a word v randomly from the word bank. Hence the word takes the value
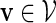 with probability q(v).
with probability q(v).Select i0 randomly from
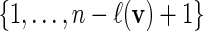 .
.Generate s0 from the stationary distribution and
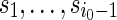 sequentially from the underlying Markov chain. Let
sequentially from the underlying Markov chain. Let 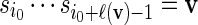 and generate
and generate 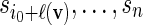 sequentially from the underlying Markov chain.
sequentially from the underlying Markov chain.
Let 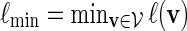 and
and 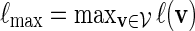 . Recall that β(v) = 0 for
. Recall that β(v) = 0 for 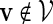 . Then
. Then
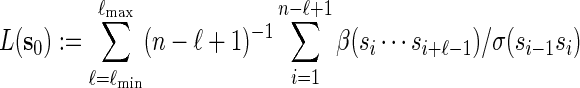 |
(2.3) |
is the likelihood ratio of generating s0 from Algorithm A and from the underlying Markov chain (with no insertion of word patterns). If Algorithm A is run independently K times, with the kth copy of s0 generated denoted by 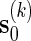 , then
, then
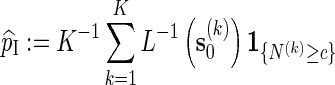 |
(2.4) |
is unbiased for pc. The term 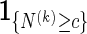 is superfluous when using Algorithm A since at least one word pattern from
is superfluous when using Algorithm A since at least one word pattern from 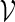 is generated in every copy of s0.
is generated in every copy of s0.
We restrict Algorithm A to c = 1 because the random insertion of more than one word patterns into the simulated sequence can result in a hard to compute likelihood ratio. To handle more general c, we use a hidden Markov model device in Algorithm B below, with hidden states Xi taking either value 0 (do not insert word pattern) or 1 (insert word pattern), so that the likelihood ratio can be computed recursively. Let
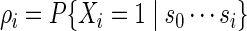 |
(2.5) |
be the word insertion probability at position i + 1 along the DNA sequence. For example, the user can simply select ρi = c/n for all i so that approximately c word patterns are inserted in each generated sequence s0. Each copy of s0 is generated in the following manner.
Algorithm B (for c ≥ 1):
Let i = 0, generate s0 from the stationary distribution and X0 satisfying (2.5).
(a) If Xi = 1, select a word v randomly from the word bank. If ℓ(v) ≤ n − i, that is, if the word v can fit into the remaining sequence, let
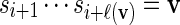 , generate Xi+ℓ(v) according to (2.5), increment i by ℓ(v) and go to step 3.
, generate Xi+ℓ(v) according to (2.5), increment i by ℓ(v) and go to step 3.(b) If the word selected in 2(a) cannot fit into the remaining sequence or if Xi = 0, generate si+1 from the underlying Markov chain and Xi+1 satisfying (2.5). Increment i by 1 and go to step 3.
If i < n, repeat step 2. Otherwise, end the recursion.
Let 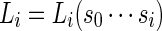 be the likelihood ratio of generating
be the likelihood ratio of generating  from Algorithm B and from the underlying Markov chain. Let
from Algorithm B and from the underlying Markov chain. Let 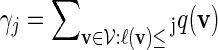 be the probability that a randomly chosen word from the word bank has length not exceeding j. Then
be the probability that a randomly chosen word from the word bank has length not exceeding j. Then
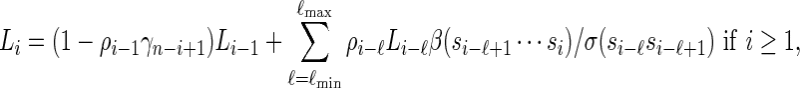 |
(2.6) |
with Li = 0 for i ≤ 0.
The estimator (2.4), with L = Ln, is unbiased if and only if all configurations of s0 satisfying N ≥ c can be generated via Algorithm B. To ensure this, it suffices for us to impose the constraint
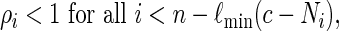 |
(2.7) |
so that we do not force the insertion of too many word patterns.
3. Palindromic Patterns and Inverted Repeats
Masse et al. (1992) reported clusters of palindromic patterns near origins of replication of viruses. There has been much work done to estimate their significance, for example, using Poisson and compound Poisson approximations (Leung et al., 1994, 2005). The four nucleotides can be divided into two complementary base pairs with a and t forming a pair and c and g forming the second pair. We denote this relation by writing ac = t, tc = a, cc = g and gc = c. For a word 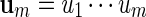 , we define its complement
, we define its complement 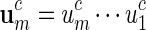 . A palindromic pattern of length ℓ = 2m is a DNA sequence that can be expressed in the form
. A palindromic pattern of length ℓ = 2m is a DNA sequence that can be expressed in the form 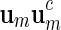 . For example, v = acgcgt is a palindromic pattern. Note that the complement of v, that is the word obtained by replacing each letter of v by its complement, is tgcgca, which is just v read backwards. This interesting property explains the terminology “palindromic pattern.”
. For example, v = acgcgt is a palindromic pattern. Note that the complement of v, that is the word obtained by replacing each letter of v by its complement, is tgcgca, which is just v read backwards. This interesting property explains the terminology “palindromic pattern.”
Inverted repeats can be derived from palindromic patterns by inserting a DNA sequence of length d in the exact middle of the pattern. The class of word patterns for inverted repeats can be expressed in the form
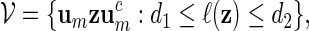 |
(3.1) |
with 0 ≤ d1 ≤ d2. When d1 = d2 = 0, then (3.1) is the class of all palindromic patterns of length 2m.
The construction of word banks for palindromic patterns is straightforward. It all boils down to generating um in some suitable manner. We advocate generating um with probability proportional to 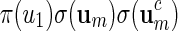 or
or 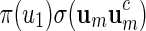 and show how this can be done in Appendix A.
and show how this can be done in Appendix A.
Having a word bank for palindromic patterns allows us to create a word bank for inverted repeats easily. The procedure is as follows.
Select
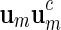 randomly from a word bank of palindromic patterns and d randomly from
randomly from a word bank of palindromic patterns and d randomly from 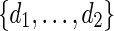 .
.Let z0 = um and generate
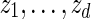 sequentially from the underlying Markov chain.
sequentially from the underlying Markov chain.Store the word
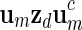 into the word bank for inverted repeats.
into the word bank for inverted repeats.
This procedure allows γj, see (2.6), to be computed easily. In particular, γj = (j − d1 + 1)/(d2 − d1 + 1) for d1 ≤ j ≤ d2, γj = 0 for j < d1 and γj = 1 for j > d2.
4. Position-Specific Weight Matrix
PSWMs are commonly used to derive fixed-length word patterns or motifs that transcription factors bind onto and usually range from four to twenty bases long. Databases such as TRANSFAC, JASPAR, and SCPD curate PSWMs for families of transcription factors. For example, the PSWM for the SWI5 transcription factor in the yeast genome (Zhu and Zhang, 1999) is
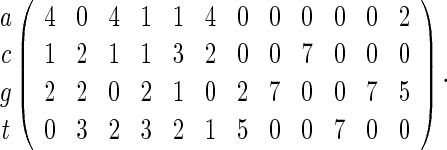 |
(4.1) |
Let wi(v) denote the entry in a PSWM that corresponds to base v at column i and let m be the number of columns in the PSWM. For any word vm (of length m), a score
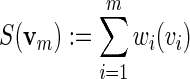 |
is computed and words with high scores are of interest. We let 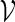 be the set of all vm with score not less than a pre-specified threshold level t. In other words,
be the set of all vm with score not less than a pre-specified threshold level t. In other words,
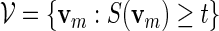 |
(4.2) |
is a set of motifs for the PSWM associated with a given transcription factor. The matrix is derived from the frequencies of the four bases at various positions of known instances of the TFBS, which are usually confirmed by biological experiments. Huang et al. (2004) provide a good review of the construction of PSWMs.
In principle, we can construct a word bank for 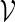 by simply generating words of length m from the underlying Markov chain and discarding words that do not belong to the motif. However, for t large, such a procedure involves discarding a large proportion of the generated words. It is more efficient to generate the words with a bias towards larger scores. In Appendix B, we show how, for any given θ > 0, a tilted Markov chain can be constructed to generate words v with probability mass function
by simply generating words of length m from the underlying Markov chain and discarding words that do not belong to the motif. However, for t large, such a procedure involves discarding a large proportion of the generated words. It is more efficient to generate the words with a bias towards larger scores. In Appendix B, we show how, for any given θ > 0, a tilted Markov chain can be constructed to generate words v with probability mass function
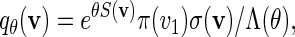 |
(4.3) |
where Λ(θ) is a computable normalizing constant. If words with scores less than t are discarded, then the probability mass function of non-discarded words is
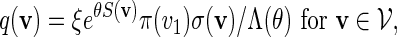 |
(4.4) |
where ξ is an unknown normalizing constant that can be estimated by the reciprocal of the fraction of non-discarded words. There are two conflicting demands placed on the choice of θ. As θ increases, the expected score of words generated under qθ(v) increases. We would thus like θ to be large so that the fraction of discarded words is small. However at the same time, we would also like θ to be small, so that the variation of β(v) = q(v)/σ(v) over  is small. Since
is small. Since
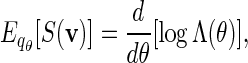 |
(4.5) |
we suggest choosing the root of the equation 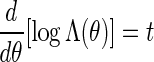 . See Appendix B for more detail on the the computation of Λ(θ) and the numerical search of the root.
. See Appendix B for more detail on the the computation of Λ(θ) and the numerical search of the root.
4.1. Example 1
We illustrate here the need for alternatives to analytical p-value approximations by applying Algorithm A on some special word patterns. Let Pπ denotes probability with v1 following stationary distribution π. Huang et al. (2004) suggested an approximation, which for c = 1 reduces to
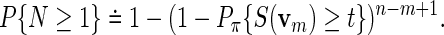 |
(4.6) |
Consider 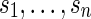 independent and identically distributed random variables taking values a, c, g and t with equal probabilities. Let
independent and identically distributed random variables taking values a, c, g and t with equal probabilities. Let
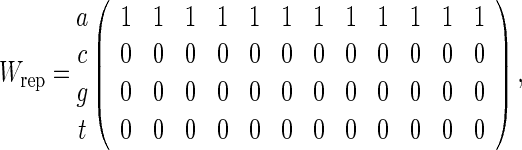 |
(4.7) |
 |
(4.8) |
and consider counting of words with score at least t for t = 9, 10 and 11. The approximation (4.6) is the same for both (4.7) and (4.8) but we know that the p-value when the PSWM is (4.7) should be smaller due to the tendency of the word patterns to clump together. Of course, declumping corrections can be applied to this special case but this is not so straightforward for general PSWMs. Table 1 compares the analytical, direct Monte Carlo and importance sampling approximations of P{N ≥ 1} for (4.7) and (4.8) with n = 200. The simulations reveal substantial over-estimation of p-values for Wrep when using (4.6). Algorithm A is able to maintain its accuracy over the range of t considered whereas direct Monte Carlo has acceptable accuracy only for t = 9.
Table 1.
Comparisons of Analytical, Direct Monte Carlo, and Importance Sampling Approximations for P{N ≥ 1} with n = 200 in Example 1
| t | 9 | 10 | 11 |
|---|---|---|---|
| Analytical | 7.1 × 10−2 | 7.1 × 10−3 | 4.2 × 10−4 |
| Wrep | |||
| Direct MC | (3.6 ± 0.6) × 10−2 | (5 ± 2) × 10−3 | 0 |
| Algorithm A | (3.0 ± 0.1) × 10−2 | (4.0 ± 0.2) × 10−3 | (2.7 ± 0.1) × 10−4 |
| Wnorep | |||
| Direct MC | (6.7 ± 0.8) × 10−2 | (9 ± 3) × 10−3 | (1 ± 1) × 10−3 |
| Algorithm A | (7.5 ± 0.2) × 10−2 | (6.9 ± 0.2) × 10−3 | (4.1 ± 0.1) × 10−4 |
Each Monte Carlo entry is obtained using 1000 simulation runs and are expressed in the form 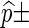 standard error.
standard error.
4.2. Example 2
We implement Algorithm B here with
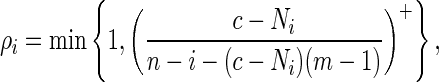 |
(4.9) |
where x+ = max{0, x}. We choose ρi in this manner to encourage word insertion when there are few bases left to be generated and the desired number of word patterns has not yet been observed. The motif consists of all words of length 12 having score at least 50 with respect to the PSWM (4.1). The transition matrix for generating the DNA sequence is
 |
(4.10) |
and the length of the sequence investigated is n = 700. We see from Table 2 variance reduction of 10–100 times in the simulation of probabilities of order 10−1 to 10−3. For smaller probabilities, direct Monte Carlo does not provide an estimate whereas estimates from the importance sampling algorithm retain their accuracy. Although importance sampling takes about two times the computing time of direct Monte Carlo for each simulation run, the savings in computing time to achieve the same level of accuracy are quite substantial.
Table 2.
 Standard Error for Example 2 with 1000 Copies of s0 Generated for Both Direct Monte Carlo and Importance Sampling Using Algorithm B
Standard Error for Example 2 with 1000 Copies of s0 Generated for Both Direct Monte Carlo and Importance Sampling Using Algorithm B
| c | Direct MC | Algorithm B |
|---|---|---|
| 1 | (9.6 ± 0.9) × 10−2 | (9.1 ± 0.3) × 10−2 |
| 2 | (3 ± 2) × 10−3 | (4.2 ± 0.2) × 10−3 |
| 3 | 0 | (1.3 ± 0.1) × 10−4 |
| 4 | 0 | (2.6 ± 0.3) × 10−6 |
5. Co-Occurrences of Motifs
For a more detailed sequence analysis of promoter regions, one can search for cis-regulatory modules (CRM) instead of single motifs. We define CRM to be a collection of fixed length motifs that are located in a fixed order in proximity to each other. They are signals for co-operative binding of transcription factors, and are important in the study of combinatorial regulation of genes. CRMs have been used successfully to gain a deeper understanding of gene regulation (Chiang et al., 2003; Zhou and Wong, 2004; Zhang et al., 2007). We focus here on the simplest type of CRM: A co-occurring pair of high scoring words separated by a gap sequence of variable length. Let S1( · ) be the score of a word of length m calculated with respect to a PSWM W1, and S2( · ) the score of a word of length r calculated with respect to a PSWM W2. Let 0 ≤ d1 < d2 < ∞ be the prescribed limits of the length of the gap and t1, t2 threshold levels for W1 and W2, respectively. The family of words for the co-occurring motifs is
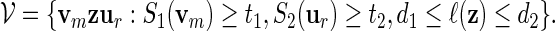 |
(5.1) |
In Section 4, we showed how word banks for the motifs 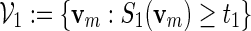 and
and 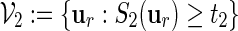 are created. Let qi be the probability mass function for
are created. Let qi be the probability mass function for 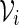 . A word bank for
. A word bank for 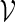 can then be created by repeating the following steps.
can then be created by repeating the following steps.
Select vm and ur independently from their respective word banks.
Select d randomly from
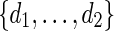 . Generate
. Generate 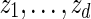 sequentially from the underlying Markov chain, initialized at z0 = vm.
sequentially from the underlying Markov chain, initialized at z0 = vm.Store w = vmzdur into the word bank.
Let q be the probability mass function of the stored words. Then
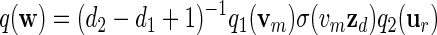 |
(5.2) |
and hence β(w) = q(w)/σ(w) = (d2 − d1 + 1)−1β1(vm)β2(ur)/σ(zdu1).
5.1. Example 3
The transcription factors SFF (with PSWM W1) and MCM1 (with PSWM W2) are regulators of the cell cycle in yeast, and are known to co-operate at close distance in the promoter regions of the genes they regulate (Spellman et al., 1998). Their PSWMs can be obtained from the database SCPD. Define 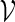 by (5.1) with t1 = 48, t2 = 110, d1 = 0 and d2 = 100. We would like to estimate the probability that the motif
by (5.1) with t1 = 48, t2 = 110, d1 = 0 and d2 = 100. We would like to estimate the probability that the motif 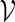 appears at least once within a promoter sequence of length n = 700. The estimated probability using Algorithm A is 3.4 × 10−3 with a standard error of 3 × 10−4. The corresponding standard error for 1000 direct Monte Carlo runs would have been about 2 × 10−3, which is large relative to the underlying probability.
appears at least once within a promoter sequence of length n = 700. The estimated probability using Algorithm A is 3.4 × 10−3 with a standard error of 3 × 10−4. The corresponding standard error for 1000 direct Monte Carlo runs would have been about 2 × 10−3, which is large relative to the underlying probability.
5.2. Structured motifs
These co-occurring motifs considered in Robin et al. (2002) consist essentially of fixed word patterns xm and yr separated by a variable length gap, with an allowance for the mutation of up to one base in xmyr. The motif can be expressed as
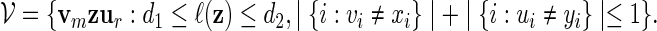 |
(5.3) |
We create a word for the word bank of 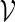 in the following manner.
in the following manner.
Select k randomly from
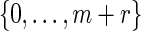 . If k = 0, then there is no mutation and we let vmur = xmyr. Otherwise, change the kth base of xmyr equally likely into one of the three other bases and denote the mutated sequence as vmur.
. If k = 0, then there is no mutation and we let vmur = xmyr. Otherwise, change the kth base of xmyr equally likely into one of the three other bases and denote the mutated sequence as vmur.Select d randomly from
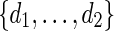 and generate the bases of
and generate the bases of 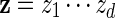 sequentially from the underlying Markov chain, initialized at z0 = vm.
sequentially from the underlying Markov chain, initialized at z0 = vm.
We perform a simulation study on eight structural motifs selected for their high frequency of occurrences in part of the Bacillus subtilis DNA dataset. We consider (d1, d2) = (16, 18) and (5, 50), with length of DNA sequence n = 100, and a Markov chain with transition matrix
 |
In Table 3, we compare importance sampling estimates of P{N ≥ 1} using Algorithm A with analytical p-value estimates from Robin et al. (2002) and direct Monte Carlo p-value estimates. The analytical p-value estimates are computed numerically via recursive methods with computation time that grows exponentially with d2 − d1, and are displayed only for the case (d1, d2) = (16, 18).
Table 3.
Comparison of Direct Monte Carlo, Importance Sampling, and Analytical Estimates of P{N ≥ 1} for Structured Motifs
| d1 | d2 | x | y | Direct MC | Algorithm A | Analytic |
|---|---|---|---|---|---|---|
| 16 | 18 | gttgaca | atataat | (2 ± 1) × 10−4 | (1.038 ± 0.006) × 10−4 | 1.01 × 10−4 |
| gttgaca | tataata | 0 | (9.00 ± 0.05) × 10−5 | 8.82 × 10−5 | ||
| tgttgac | tataata | (20 ± 10) × 10−5 | (9.39 ± 0.05) × 10−5 | 9.20 × 10−5 | ||
| ttgaca | ttataat | (9 ± 3) × 10−4 | (6.65 ± 0.03) × 10−4 | 6.55 × 10−4 | ||
| ttgacaa | tacaat | (4 ± 2) × 10−4 | (4.64 ± 0.02) × 10−4 | 4.57 × 10−4 | ||
| ttgacaa | tataata | (2 ± 1) × 10−4 | (1.798 ± 0.009) × 10−4 | 1.78 × 10−4 | ||
| ttgacag | tataat | (5 ± 2) × 10−4 | (3.62 ± 0.02) × 10−4 | 3.59 × 10−4 | ||
| ttgacg | tataat | (10 × 3) × 10−4 | (9.90 ± 0.06) × 10−4 | 9.76 × 10−4 | ||
| combined p-value | (2.0 ± 0.4) × 10−3 | (2.96 ± 0.03) × 10−3 | ||||
| 5 | 50 | gttgaca | atataat | (1 ± 0.3) × 10−3 | (1.265 ± 0.008) × 10−3 | |
| gttgaca | tataata | (0.4 ± 0.2) × 10−3 | (1.103 ± 0.007) × 10−3 | |||
| tgttgac | tataata | (1.8 ± 0.4) × 10−3 | (1.150 ± 0.007) × 10−3 | |||
| ttgaca | ttataat | (7.4 ± 0.9) × 10−3 | (7.88 ± 0.05) × 10−3 | |||
| ttgacaa | tacaat | (5.0 ± 0.7) × 10−3 | (5.50 ± 0.04) × 10−3 | |||
| ttgacaa | tataata | (1.5 ± 0.4) × 10−3 | (2.21 ± 0.01) × 10−3 | |||
| ttgacag | tataat | (3.1 ± 0.6) × 10−3 | (4.23 ± 0.03) × 10−3 | |||
| ttgacg | tataat | (0.9 ± 0.1) × 10−2 | (1.126 ± 0.008) × 10−2 | |||
| combined p-value | (2.7 ± 0.2) × 10−2 | (3.30 ± 0.04) × 10−2 | ||||
For both direct Monte Carlo and importance sampling, 10,000 simulation runs are executed for each entry and the results are displayed in the form 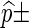 standard error.
standard error.
We illustrate here how the importance sampling algorithms can be modified to handle more complex situations, for example, to obtain a combined p-value for all eight motifs. Consider more generally p = P{max1≤j≤J(N(j) − cj) ≥ 0}, where N(j) is the total word count from the motif 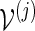 and cj is a positive integer. Let L(j) be the likelihood ratio when applying either Algorithm A or B with insertion of words from
and cj is a positive integer. Let L(j) be the likelihood ratio when applying either Algorithm A or B with insertion of words from 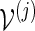 . For the kth simulation run, we execute the following steps.
. For the kth simulation run, we execute the following steps.
Select jk randomly from
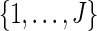 .
.Generate
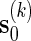 using either Algorithm A or B, with insertion of words from
using either Algorithm A or B, with insertion of words from 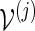 .
.
Then
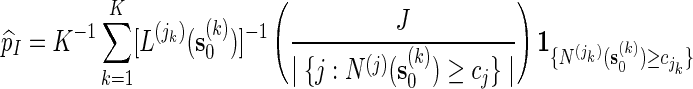 |
(5.4) |
is unbiased for p (see Appendix C). The key feature in (5.4) is the correction term 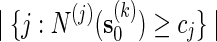 . Without this term,
. Without this term, 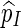 is an unbiased estimator for the Bonferroni upper bound
is an unbiased estimator for the Bonferroni upper bound 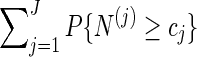 . The correction term adjusts the estimator downwards when more than one thresholds cj are exceeded.
. The correction term adjusts the estimator downwards when more than one thresholds cj are exceeded.
We see from Table 3 that the variance reduction is substantial when importance sampling is used. In fact, the direct Monte Carlo estimate is often unreliable. Such savings in computation time is valuable both to the end user and also to the researcher trying to test the reliability of his or her analytical estimates on small p-values. We observe for example that the numerical estimates for (d1, d2) = (16, 18) given in Robin et al. (2002) are quite accurate but tends to underestimate the true underlying probability.
6. Discussion
The examples given here are not meant to be exhaustive but they do indicate how we can proceed in situations not covered here. For example, if we would like the order of the two words in a CRM to be arbitrary, we can include an additional permutation step in the construction of the word bank. In Section 5.2, we also showed how to simulate p-values of the maximum count over a set of word patterns. As we gain biological understanding, the models that we formulate for DNA and protein functional sites become more complex. Over the years, they have evolved from deterministic words to consensus sequences to PSWMs and then to motif modules. As probabilistic models for promoter architecture gets more complex and context specific, importance sampling methods are likely to be more widely adopted in the computation of p-values.
7. Appendix
A. Generating palindromes and invented repeats
We first show how words vm can be generated with probability mass function
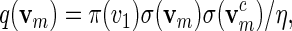 |
with 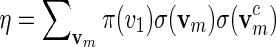 a computable normalizing constant. Apply the backward recursive relations
a computable normalizing constant. Apply the backward recursive relations
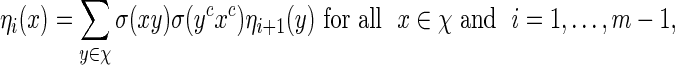 |
(A.1) |
initialized with ηm(x) = 1 for all x. Then 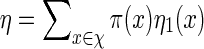 . Let Q be the desired probability measure for generating vm with probability mass function q. Then the Markovian property
. Let Q be the desired probability measure for generating vm with probability mass function q. Then the Markovian property
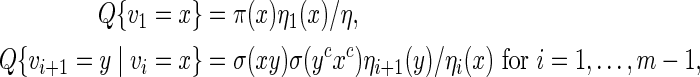 |
(A.2) |
allows us to generate vi sequentially via transition matrices.
To generate words vm with probability mass function 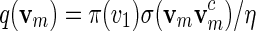 , let ηm(x) = σ(xxc) instead of ηm(x) = 1 and proceed with (A.1) and (A.2).
, let ηm(x) = σ(xxc) instead of ηm(x) = 1 and proceed with (A.1) and (A.2).
B. Generating highscoring motifs from PSWMs
Let S be the score with respect to a given PSWM W and let θ > 0. We provide here a quick recursive algorithm for generating vm from the probability mass function
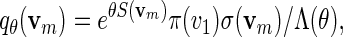 |
(A.3) |
with Λ(θ) = ΣvmeθS(vm)π(v1)σ(vm) a computable normalizing constant. Since log Λ(θ) is convex, the solution of 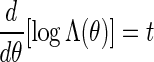 can be found using a bijection search. We take note of the backward recursive relations
can be found using a bijection search. We take note of the backward recursive relations
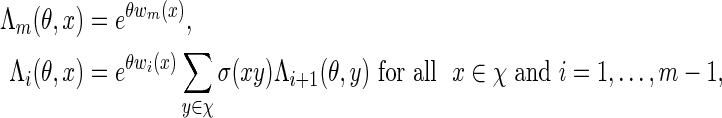 |
(A.4) |
from which we can compute 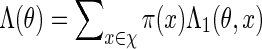 . Let Q denote the desired probability measure for generating
. Let Q denote the desired probability measure for generating 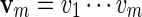 from qθ. By (A.3) and (A.4), we can simply generate the letters vi sequentially, using transition matrices defined by the Markovian relations
from qθ. By (A.3) and (A.4), we can simply generate the letters vi sequentially, using transition matrices defined by the Markovian relations
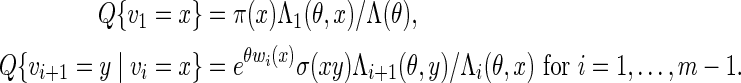 |
(A.5) |
C. Unbiasedness of 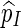 in (5.4)
in (5.4)
We shall show here that 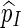 in (5.4) is unbiased for p = P{max1≤j≤J(N(j) − cj) ≥ 0}. Let Aj = {s0 : N(j)(s0) ≥ cj} and let Qj be a probability measure such that L(j)(s0) = Qj(s0)/P(s0) > 0 for any s0
in (5.4) is unbiased for p = P{max1≤j≤J(N(j) − cj) ≥ 0}. Let Aj = {s0 : N(j)(s0) ≥ cj} and let Qj be a probability measure such that L(j)(s0) = Qj(s0)/P(s0) > 0 for any s0
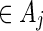 . Let
. Let 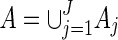 . Then with the convention 0/0 = 0,
. Then with the convention 0/0 = 0,
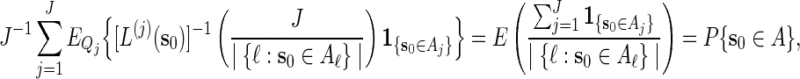 |
and hence 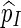 is indeed unbiased.
is indeed unbiased.
D. Asymptotic optimality
To estimate p := P{N(s) ≥ c} using direct Monte Carlo, simply generate K independent copies of s, denoted by 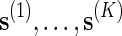 , under the original probability measure P, and let
, under the original probability measure P, and let
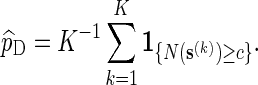 |
To simulate p using importance sampling, we need to first select a probability measure Q ≠ P for generating 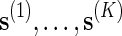 . The estimate of p is then
. The estimate of p is then
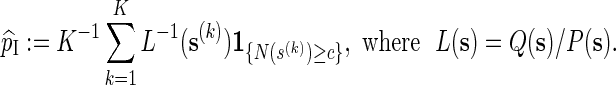 |
We require Q(s) > 0 whenever N(s) ≥ c, so as to ensure that 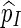 is unbiased for p.
is unbiased for p.
The relative error (RE) of a Monte Carlo estimator 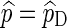 or
or 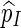 , is given by
, is given by 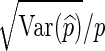 . We say that
. We say that 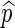 is asymptotically optimal if for any
is asymptotically optimal if for any 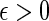 , we can satisfy
, we can satisfy 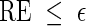 with log K = o(| log p|) as p → 0 (Sadowsky and Bucklew, 1990; Dupuis and Wang, 2005). Since
with log K = o(| log p|) as p → 0 (Sadowsky and Bucklew, 1990; Dupuis and Wang, 2005). Since 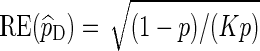 , direct Monte Carlo is not asymptotically optimal. The question we would like to answer here is: Under what conditions are Algorithms A and B asymptotically optimal?
, direct Monte Carlo is not asymptotically optimal. The question we would like to answer here is: Under what conditions are Algorithms A and B asymptotically optimal?
The examples described in Sections 3–5 involve word families that can be characterized as 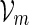 . We may also include an additional subscript m to a previously defined quantity to highlight its dependence on m, for example pm, qm, βm and nm. We say that xm and ym have similar logarithmic value relative to m, and write xm ≃ ym, if | log xm − log ym| = o(m) as m → ∞ . It is not hard to see that if xm ≃ ym and ym ≃ zm, then xm ≃ zm. In Algorithm A, it is assumed implicitly that
. We may also include an additional subscript m to a previously defined quantity to highlight its dependence on m, for example pm, qm, βm and nm. We say that xm and ym have similar logarithmic value relative to m, and write xm ≃ ym, if | log xm − log ym| = o(m) as m → ∞ . It is not hard to see that if xm ≃ ym and ym ≃ zm, then xm ≃ zm. In Algorithm A, it is assumed implicitly that 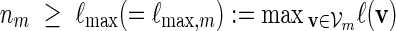 and we shall also assume nm ≥ cℓmax when using Algorithm B. To fix the situation, let ρi = c/nm for all i in Algorithm B. Let
and we shall also assume nm ≥ cℓmax when using Algorithm B. To fix the situation, let ρi = c/nm for all i in Algorithm B. Let 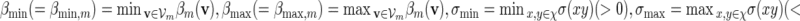 and
and 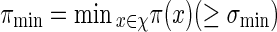 . Let
. Let 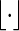 denote the greatest integer function, Px denote probability conditioned on s1 = x or v1 = x and Pπ denote probability conditioned on s1 or v1 following the stationary distribution.
denote the greatest integer function, Px denote probability conditioned on s1 = x or v1 = x and Pπ denote probability conditioned on s1 or v1 following the stationary distribution.
In the following lemma, we provide conditions for asymptotic optimality and check them in Appendices D.1–D.3 for the word families discussed in Sections 3–5.
Lemma 1
If log nm ≃ 1 and
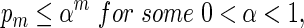 |
(A.6) |
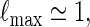 |
(A.7) |
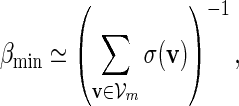 |
(A.8) |
then both Algorithms A and B are asymptotically optimal.
Proof. Let 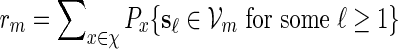 . Since
. Since 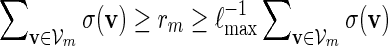 , by (A.7) and (A.8),
, by (A.7) and (A.8),
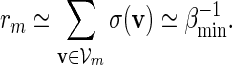 |
(A.9) |
By (6.1), | log pm| ≥ m| log α| for all large m and hence it suffices for us to show Km ≃ 1.
If nm ≃ 1, then by (A.9) and the inequalities 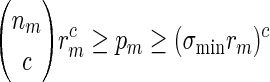 ,
,
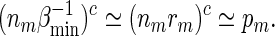 |
(A.10) |
Consider next the case nm/ℓmax → ∞ . Since lognm ≃ 1, there exists integers ξm such that ξm ≃ 1, ξm = o(nm) and log nm = o(ξm). Let κm = ⌊ nm/(ℓmax + ξm) ⌋ and 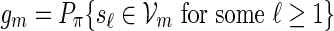 . By (A.6), αm ≥ pm ≥ (gmσmin)c and hence gm → 0. Since the underlying Markov chain is uniformly ergodic,
. By (A.6), αm ≥ pm ≥ (gmσmin)c and hence gm → 0. Since the underlying Markov chain is uniformly ergodic,
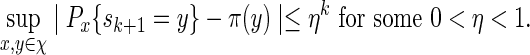 |
(A.11) |
By considering the sub-cases of at least c words 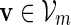 starting at positions 1,
starting at positions 1, 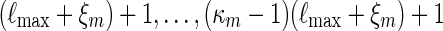 , it follows from (A.11) that
, it follows from (A.11) that
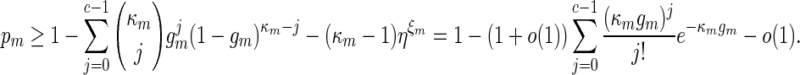 |
By (A.6), κmgm → 0 and this implies κmrm → 0. Since (ℓmax + ξm) ≃ 1, it follows that κm ≃ nm and hence by the inequalities
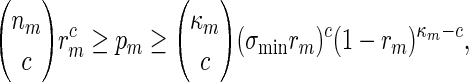 |
(A.10) again holds. By using a subsequence argument if necessary, it follows that (A.10) holds as long as log nm ≃ 1.
For Algorithm A, by (2.3) and (2.4),
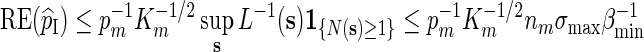 |
and the desired relation Km ≃ 1 follows from (A.10) with c = 1.
For Algorithm B, it follows from (2.6) that if N(s) ≥ c, then L(s) ≥ (1 − c/nm)nm [cβmin /(nmσmax)]c and hence by (2.4),
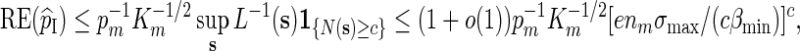 |
and again Km ≃ 1 follows from (A.10). ▪
D.1. Inverted repeats
Consider the word family (3.1) with d2 ≃ 1. Then (A.7) holds. Since 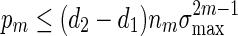 , (A.6) holds when nm = O(γm) for some
, (A.6) holds when nm = O(γm) for some 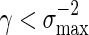 . It remains to check (A.8). Since
. It remains to check (A.8). Since 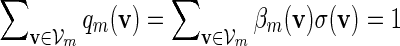 ,
,
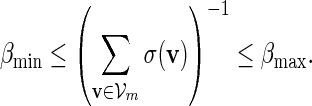 |
(A.12) |
Let um be generated with probability proportional to 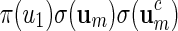 when creating the word bank
when creating the word bank 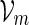 . Then there exists a constant C > 0 such that
. Then there exists a constant C > 0 such that
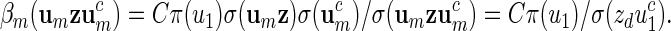 |
D.2. Word patterns derived from PSWMs
For the word family (4.2), condition (A.7) is always satisfied. Let the entries of the PSWM be non-negative integers and assume that the column totals are fixed at some C > 0. It follows from large deviations theory (Dembo and Zeitouni, 1998) that if t( = tm) ≥ EπS(v) + ζm for some ζ > 0, then
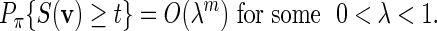 |
(A.13) |
Since pm ≤ nmPπ{S(v) ≥ t}, (A.6) holds if nm = O(γm) for some γ < λ −1.
To simplify the analysis in checking (A.8), select the tilting parameter θ( = θm) to be the root of Eqθ[S(v)] = t + δm for some positive δm = o(m) satisfying m−1/2δm → ∞ as m → ∞ , instead of the root of Eqθ[S(v)] = t, as suggested in the statement containing (4.5). The implicit assumption is that 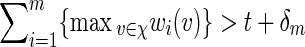 for all m. Since the entries of the transition matrices derived in Appendix B are uniformly bounded away from zero, it follows from a coupling argument that Covqθ(wi(vi),wj(vj)) = O(τ|i−j|) for some 0 < τ < 1 and hence Varqθ(S(v)) = O(m). By (4.3) and Chebyshev's inequality,
for all m. Since the entries of the transition matrices derived in Appendix B are uniformly bounded away from zero, it follows from a coupling argument that Covqθ(wi(vi),wj(vj)) = O(τ|i−j|) for some 0 < τ < 1 and hence Varqθ(S(v)) = O(m). By (4.3) and Chebyshev's inequality,
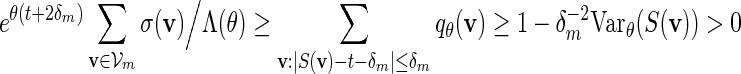 |
(A.14) |
for all large m. Since ξ > 1 in (4.4), 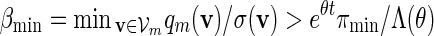 and (A.8) follows from (A.12) and (A.14).
and (A.8) follows from (A.12) and (A.14).
D.3. Co-occurrences of motifs
Consider the word family (5.1) with (r/m) bounded away from zero and infinity and d2 ≃ 1. We check that (A.7) holds. If t1 ≥ ES1(v) + ζm for some ζ > 0, then (A.13) holds with S replaced by S1, t replaced by t1 and hence (A.6) holds if nm = O(γm) for some γ < λ−1.
Let θj be the root of Eθj[Sj(v)] = tj + δm for some positive δm = o(m) with m1/2δm → ∞ , j = 1 and 2, assuming that 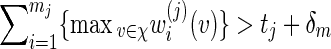 , where m1 = m and m2 = r. Let
, where m1 = m and m2 = r. Let 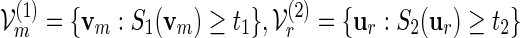 and let Λ(1)(θ1), Λ(2)(θ2) be their respective normalizing constants, see (4.3). By the arguments in (A.14),
and let Λ(1)(θ1), Λ(2)(θ2) be their respective normalizing constants, see (4.3). By the arguments in (A.14),
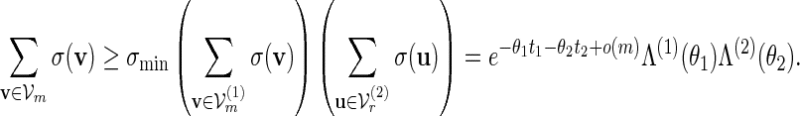 |
Acknowledgments
This research was partially supported by the National University of Singapore (grants C-389-000-010-101 and R-155-062-112).
Disclosure Statement
No competing financial interests exist.
References
- Chan H.P. Zhang N.R. Scan statistics with weighted observations. J. Am. Statist. Assoc. 2007;102:595–602. [Google Scholar]
- Chiang D.Y. Moses A.M. Kellis M., et al. Phylogenetically and spatially conserved word pairs associated with gene-expression changes in yeasts. Genome Biol. 2003;4:R43. doi: 10.1186/gb-2003-4-7-r43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cottrell M. Fort J.C. Malgouyres G. Large deviations and rare events in the study of stochastic algorithms. IEEE Trans. Automat. Contr. 1983;28:907–920. [Google Scholar]
- Dembo A. Zeitouni O. Large Deviations: Techniques and Applications. Springer; New York: 1998. [Google Scholar]
- Do K.A. Hall P. Distribution estimating using concomitant of order statistics, with applications to Monte Carlo simulation for the bootstrap. J.R. Statist. Soc. B. 1992;54:595–607. [Google Scholar]
- Dupuis P. Wang H. Dynamic importance sampling for uniformly recurrent Markov chains. Ann. Appl. Probabil. 2005;15:1–38. [Google Scholar]
- Fuh C.D. Hu I. Efficient importance sampling for events of moderate deviations with applications. Biometrika. 2004;91:471–490. [Google Scholar]
- Gusfield D. Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology. Cambridge University Press; London: 1997. [Google Scholar]
- Huang H. Kao M. Zhou X., et al. Determination of local statistical significance of patterns in Markov sequences with applications to promoter element identification. J. Comput. Biol. 2004;11:1–14. doi: 10.1089/106652704773416858. [DOI] [PubMed] [Google Scholar]
- Johns M.V. Importance sampling for bootstrap confidence intervals. J. Am. Statist. Assoc. 1988;83:709–714. [Google Scholar]
- Lai T.L. Shan J.Z. Efficient recursive algorithms for detection of abrupt changes insignals and control systems. IEEE Trans. Automat. Contr. 1999;44:952–966. [Google Scholar]
- Leung M.Y. Choi K.P. Xia A, et al. Nonrandom clusters of palindromes in herpesvirus genomes. J. Comput. Biol. 2005;12:331–354. doi: 10.1089/cmb.2005.12.331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leung M.Y. Schachtel G.A. Yu H.S. Scan statistics and DNA sequence analysis: the search for an origin of replication in a virus. Nonlinear World. 1994;1:445–471. [Google Scholar]
- Masse M.J.O. Karlin S. Schachtel G.A., et al. Human cytomegalovirus origin of DNA replication (oriLyt) resides within a highly complex repetitive region. Proc. Natl Acad. Sci. USA. 1992;89:5246–5250. doi: 10.1073/pnas.89.12.5246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitrophanov A.Y. Borodovsky M. Statistical significance in biological sequence analysis. Briefings Bioinform. 2006;7:2–24. doi: 10.1093/bib/bbk001. [DOI] [PubMed] [Google Scholar]
- Pape U. Rahmann S. Sun F., et al. Compound Poisson approximation of the number of occurrences of a position frequency matrix (PFM) on both strands. J. Comput. Biol. 2008;15:547–564. doi: 10.1089/cmb.2007.0084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prum B. Rodolphe F. de Turckheim E. Finding words with unexpected frequencies in deoxyribonucleic acid sequences. J.R. Statist. Soc. B. 1995;57:205–220. [Google Scholar]
- Régnier M. A unified approach to word occurrence probabilities. Dis. Appl. Math. 2000;104:259–280. [Google Scholar]
- Reinert G. Schbath S. Waterman M. Probabilistic and statistical properties of words: an overview. J. Comput. Biol. 2000;7:1–46. doi: 10.1089/10665270050081360. [DOI] [PubMed] [Google Scholar]
- Robin S. Daudin J. Richard H., et al. Occurrence probability of structured motifs in random sequences. J. Comput. Biol. 2002;9:761–773. doi: 10.1089/10665270260518254. [DOI] [PubMed] [Google Scholar]
- Sadowsky J.S. Bucklew J.A. On large deviations theory and asymptotically efficient Monte Carlo estimation. IEEE Trans. Inform. Theory. 1990;36:579–588. [Google Scholar]
- Siegmund D. Importance sampling in the Monte Carlo study of sequential test. Ann. Statist. 1976;4:673–684. [Google Scholar]
- Spellman P.T. Sherlock G. Zhang M.Q., et al. Comprehensive identification of cell cycle–regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol. Biol. Cell. 1998;9:3273–3297. doi: 10.1091/mbc.9.12.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang N.R. Wildermuth M.C. Speed T.P. Transcription factor binding site prediction with multivariate gene expression data. Ann. Appl. Statist. 2008;2:332–365. [Google Scholar]
- Zhou Q. Wong W. CisModule: de novo discovery of cis-regulatory modules by hierarchical mixture modeling. Proc. Natl Acad. Sci. USA. 2004;101:12114–112119. doi: 10.1073/pnas.0402858101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J. Zhang M.Q. SCPD: a promoter database of the yeast Saccharomyces cerevisiae. Bioinformatics. 1999;15:607–611. doi: 10.1093/bioinformatics/15.7.607. [DOI] [PubMed] [Google Scholar]