A Bayesian approach to strengthen inference for case-control studies with multiple error-prone exposure assessments

Abstract

In case-control studies, exposure assessments are almost always error-prone. In the absence of a gold standard, two or more assessment approaches are often used to classify people with respect to exposure. Each imperfect assessment tool may lead to misclassification of exposure assignment; the exposure misclassification may be differential with respect to case status or not; and, the errors in exposure classification under the different approaches may be independent (conditional upon the true exposure status) or not. Although methods have been proposed to study diagnostic accuracy in the absence of a gold standard, these methods are infrequently used in case-control studies to correct exposure misclassification that is simultaneously differential and dependent. In this paper, we proposed a Bayesian method to estimate the measurement-error corrected exposure-disease association, accounting for both differential and dependent misclassification. The performance of the proposed method is investigated using simulations, which show that the proposed approach works well, as well as an application to a case-control study assessing the association between asbestos exposure and mesothelioma.

1. INTRODUCTION

Misclassification of exposure status is ubiquitous in case-control studies [1], which can bias the association between an exposure and a disease. Misclassification of people with respect to exposure can be either differential with respect to case status, or nondifferential. In many health studies, a gold standard exposure assessment may not exist or is too costly to obtain. In this situation, it is common to apply two or more imperfect assessments to evaluate exposure status. When multiple error-prone exposure assessments are used, misclassification can be conditionally independent or dependent given the latent exposure status, i.e., multiple exposure assessments are conditionally independent or dependent given the latent exposure status, respectively. Misspecification of differential/nondifferential and/or dependent/independent misclassification can lead to biased estimation of the exposure-disease association [2].

A considerable literature is available on statistical methods to assess the diagnostic accuracy of multiple binary disease measurements focusing on dependent/independent misclassification. For example, Hui and Walter [3] proposed a maximum likelihood-based method to estimate the sensitivities and specificities of two imperfect measurements with two populations under conditional independence assumption of test results given the underlying disease status. Vacek [4], Torrrance-Rynard and Walter [5] showed that parameter estimators can be biased when conditional independence is falsely assumed, and correlation between multiple measurements conditioning on the latent disease status may exist in practice. Several methods have been proposed to incorporate conditional dependence across multiple imperfect measurements. As examples, Espeland and Handelman [6] proposed a log-linear modeling approach; Qu, Tan, and Kutner [7] proposed a Gaussian random effects model (GRE); Yang and Becker [8] proposed a marginal approach; Albert and Dodd [9] proposed a finite mixture (FM) model; Xu and Craig [10] proposed a probit latent class model with general correlation structures.

Some authors have written about differential/nondifferential misclassification. When multiple or repeated imperfect measurements were used to assess exposure status in case-control studies, non-differential misclassification was commonly assumed in previous studies [11, 12]. But in practice, differential misclassification may arise from sources such as exposure recall bias, interviewers who are not blinded to case status, or differences in completeness or quality of information used for exposure assessments when cases are sick or deceased while controls are not. Many existing studies have shown that differential misclassification may bias the magnitude of exposure-disease association and can substantially affect the power of statistical tests [13, 14].

However, to the best of our knowledge, few methods are available to simultaneously account for differential and conditionally dependent misclassification. Chu et al. [2] proposed a maximum likelihood-based frequentist approach accounting for both differential and conditionally dependent misclassification. However, when the number of exposure classification approaches is less than four, the approach proposed by Chu et al. can only allow a partially differential and constrained dependent model due to the issue of non-identifiability [15], which will be described in details in Section 3. In this paper, we propose a Bayesian approach to simultaneously consider both differential and dependent misclassification. By using informative priors for select parameters, which are commonly available based on the literature or expert opinion, the proposed Bayesian methods allow us to simultaneously explore differential and dependent misclassification even when there are only two or three exposure assessment approaches. In addition, the Bayesian approach provides a natural way to combine prior information with current data to make posterior inferences that are “exact” without relying on asymptotic approximations [16, 17], and provides better small sample inference and direct construction of 100 (1–α)% equal tail and/or highest probability density (HPD) intervals on general functions of parameters. The remainder of this paper is organized as follows. In Section 2, we introduce an occupational case-control study to evaluate the association between asbestos exposure and mesothelioma [18], which was previously analyzed by Chu et al [2] using a frequentist approach. In Section 3, we present the Bayesian approach to simultaneously consider both differential and dependent mis-classification. This paper solely focuses on the situation in which the exposure classification is binary (i.e., assessment of whether or not the case/control was exposed to the hazard). Other situations including categorical, ordinal, and continuous exposure assessments will be considered in the future study. In Section 4, we present the results of the analysis for the study in section 2 using the proposed Bayesian approach. The performance of our proposed Bayesian method is investigated through a series of simulations in Section 5. Finally we conclude with a discussion in Section 6.

2. ASBESTOS EXPOSURE AND MESOTHELIOMA: A CASE STUDY

A population-based case-control study was conducted to assess the association between asbestos exposure and mesothelioma [18]. Cases were selected from 3 sources between 1975 and 1980: the New York State Health Department Cancer Registry, the Los Angeles County Cancer Surveillance Program, and 39 Veterans Administration Hospitals. Controls were selected from the same geographical area (New York, Los Angeles) or the same hospital. Table 1 presents the frequency of the number of participants cross-tabulated by the three exposure assessments (i.e., by next-of-kin assessment, expert assessment by an industrial hygienist, and by use of a generic job-exposure matrix) as well as the case/control status. The odds ratios (OR) for the association between asbestos exposure and mesothelioma were estimated to be 10.74 (95% confidence limits: 7.27, 15.94), 4.65 (95% CL: 3.19, 6.77) and 2.06 (95% CL: 1.48, 2.86) by these three methods respectively. However, each of these estimates likely suffers bias due to asbestos exposure that may be differential with respect to case status and that may be conditionally dependent given the latent exposure status. Using a frequentist maximum-likelihood based method, Chu et al. [2] estimated an OR of 16.12 (95% confidence limits: 5.22, 27.03) using a partially differential and dependent misclassification model. However, due to non-identifiability issue when the number of binary exposure assessments is less than four, their analyses are restricted. In Section 4, we use the fully Bayesian approach described in next section with informative priors on select sensitivity and specificity parameters, estimated from literature, to explore a full differential and dependent model and make posterior inference.

Table 1.

A case-control study of asbestos and mesothelioma from the National Occupational Hazard Survey

Exposure test positive (+) or negative (–)			Number of subjects
Next-of-kin respondents (Y1)	Expert assessment (Y2)	Job-exposure matrix (Y3)	Cases (D = 1)	Controls (D = 0)
+	+	+	69	36
+	+	–	47	14
+	–	+	0	4
+	–	–	1	3
–	+	+	22	82
–	+	–	28	113
–	–	+	7	39
–	–	–	34	242
	Total		208	533

3. STATISTICAL METHODS

3.1 The Likelihood and Full Posterior Distribution

Let Y_ij be the classification result (with value 1 indicating positive result and 0 indicating negative result) of the j^th of J exposure assessments for individual i (i = 1, ..., N) and D_i be the disease status (with value 1 indicating a case and 0 indicating a control) for individual i (i = 1, ..., N). Let the latent variable E_i denote the true exposure status with 1 representing exposed and 0 representing unexposed. Let π_i denote the probability of being truly exposed for the i^th subject. A logistic regression logit(π_i) = logit(Pr(E_i = 1)) = η₀ + η₁D_i was considered to model the probability of being truly exposed given the disease status. The odds ratio (OR) of exposure between diseased and non-diseased is thus OR = e^η₁. Because each subject is evaluated by 2 or more imperfect exposure assessments, a correlation in exposure misclassification could be present. This correlation can be accommodated by a latent continuous variable Z_i, which varies from subject to subject and has a Gaussian distribution with zero mean and unit variance. The positive result for the j^th assessment is assumed to depend on both the latent true exposure status E_i of the i^th subject and the Gaussian latent variable Z_i, through a generalized linear mixed regression model, such as a probit model,

$$P(Y_{ij}=1\mid E_i=e_i,D_i=d_i,Z_i=z_i)=\Phi (a_{e_{i}j}+b_{e_{i}j}{d}_i+c_{e_{i}j}{z}_i),$$ (3.1)

where e_i = 0, 1, d_i = 0, 1, and Z_i ~ N(0, 1) [7, 19]. Here the latent Gaussian random variable Z_i is assumed to be independent to the disease status D_i and the latent exposure status E_i. Now let Se_dj and Sp_dj denote the sensitivity and specificity for the j^th assessment in the d^th disease group, then

$$\begin{array}{cc}\hfill S{e}_{d_{i}j}& =\mathrm{P}({\mathrm{Y}}_{\mathrm{ij}}=1\mid {\mathrm{E}}_i=1,{\mathrm{D}}_i={\mathrm{d}}_i)={\int }_{-\infty }^{+\infty }\Phi (a_{1j}+b_{1j}{d}_i+c_{1j}{z}_i)d\Phi \left(z_i\right)=\Phi \left(\frac{a_{1j}+b_{1j}{d}_i}{\sqrt{1+c_{1j}^2}}\right),\hfill \\ \hfill S{p}_{d_{i}j}& =\mathrm{P}({\mathrm{Y}}_{\mathrm{ij}}=0\mid E_i=0,{\mathrm{D}}_i={\mathrm{d}}_i)=1-{\int }_{-\infty }^{+\infty }\Phi (a_{0j}+b_{0j}{d}_i+c_{0j}{z}_i)d\Phi \left(z_i\right)=1-\Phi \left(\frac{a_{0j}+b_{0j}{d}_i}{\sqrt{1+c_{0j}^2}}\right).\hfill \end{array}$$ (3.2)

Formula (3.2) is based on the full model (3.1), which encompasses both fully differential (b_eij ≠ 0) and fully dependent (c_eij ≠ 0) misclassification. If b_eij = 0 for all e_i and j, it is called non-differential exposure misclassification; if b_eij = 0 for some e_i and j, it is called partially differential exposure misclassification. If c_eij = 0 for all e_i and j, it is called conditionally independent; If c_eij = 0 for some e_i and j, it is called partially conditionally dependent.

Usually certain constraints are put on the parameters c_eij [7]. For example, a very important “special” or “simplified” case is the model with equal variance components for the subgroups of the study population that are truly exposed and unexposed, which corresponds to c_eij = c_ei for all j.

Assuming that the multiple exposure assessments are conditionally independent given the latent exposure status E_iand latent Gaussian random variable Z_i, the probability of observing Y_i = (y_i1, y_i2,..., y_iJ) for the i^th subject is

$$p(y_{i1},y_{i2},\dots ,y_{iJ})={\int }_{-\infty }^{+\infty }\{{\pi }_{i}p(y_{i1},y_{i2},\dots ,y_{iJ}\mid E_i=1,z_i)+(1-{\pi }_i)p(y_{i1},y_{i2},\dots ,y_{iJ}\mid E_i=0,z_i)\}d\Phi \left(z_i\right)={\pi }_i{\int }_{-\infty }^{+\infty }\prod _{j=1}^J\left\{\Phi {\left(a_{1j}+b_{1j}{d}_i+c_{1j}{z}_i\right)}^{y_{ij}}{\left[1-\Phi \left(a_{1j}+b_{1j}{d}_i+c_{1j}{z}_i\right)\right]}^{1-y_{ij}}\right\}d\Phi \left(z_i\right)+(1-{\pi }_i){\int }_{-\infty }^{+\infty }\prod _{j=1}^J\left\{\Phi {\left(a_{0j}+b_{0j}{d}_i+c_{0j}{z}_i\right)}^{y_{ij}}{\left[1-\Phi \left(a_{0j}+b_{0j}{d}_i+c_{0j}{z}_i\right)\right]}^{1-y_{ij}}\right\}d\Phi \left(z_i\right).$$ (3.3)

Let θ = (η_di, a_eij, b_eij, c_eij) and let f(θ) be joint prior distribution, the joint posterior distribution of θ is proportional to ${\prod }_{i=1}^{N}P(y_{i1},y_{i2},\dots ,y_{iJ})\times f\left(\theta \right)$.

In most instances, inferences obtained by Bayesian and frequentist methods agree when weak prior distributions are specified. The Bayesian framework is particularly attractive when suitable proper prior distributions can be constructed to incorporate known constraints and subject-matter knowledge on model parameters [16, 17, 20].

3.2 The Identifiability of Proposed Models

Here, we briefly discuss the non-identifiability issue for the proposed models. If there are J binary exposure assessments that classify each participant with respect to exposure, then there are 2^J possible combinations of classifications of exposure status. For a fixed number of participants, there are 2^J+1 – 2 degrees of freedom in a case-control study (i.e. the maximum number of parameters that can be estimated). However, the full model (see equation 3.1) has 6J + 2 unknown parameters. Thus it inhibits us exploring differential and dependent misclassification simultaneously when J <4. For example, when J = 3, only 14 parameters can be estimated, allowing for a full exploration of either differential or conditionally dependent misclassification, but not both, or an exploration of partial differential and partial conditionally dependent misclassification (Chu et al. 2009). Thus in the frequentist setting, the model in equation 3.1 is not identifiable when J <4. However, in the Bayesian setting, the model can still be identified by specifying informative priors on some of the parameters [15]. For example, the sensitivity and specificity parameters of different exposure assessments for the general population are commonly available from the literature of previous studies. With informative priors for at least the number of parameters that are unidentifiable in the frequentist setting, the proposed Bayesian methods allow us to simultaneously explore differential and dependent misclassification even when the number of binary exposure assessments J <4. In this situation, the posterior distributions are strongly dependent on the prior information [15, 21].

3.3 Posterior Computation using the Markov chain Monte Carlo method

Posterior computation was done using free downloadable software WinBUGS (http://www.mrc-bsu.cam.ac.uk/bugs) and BRugs library in R (http://www.r-project.org/). Model code is available upon request. The burn-in consisted of 20,000 iterations, and 50,000 subsequent iterations were used for posterior summaries. Convergence of Markov chain Monte Carlo (MCMC) was assessed using the Gelman and Rubin convergence statistic [22, 23]. The posterior credible intervals for the sensitivities, specificities and odds ratio are directly available from the posterior distributions approximated by the posterior samples using the MCMC chains. Deviance Information Criterion (DIC) [24], was used as a guide to select the final model for posterior inference. The deviance, up to an additive quantity not depending upon θ, is D(θ) = –2log L(Data | θ), where L(Data | θ) is the likelihood for the respective model. The DIC is given by $\overline{D\left(\theta \right)}+p_D$, where $\overline{D\left(\theta \right)}=E_{\theta \mid Data}\left[D\left(\theta \right)\right]$ is the Bayesian deviance, and $p_D=\overline{D\left(\theta \right)}-D\left(\overline{\theta }\right)$ is the effective number of model parameters. It rewards better fitting models through the first term and penalizes more complex models through the second term. A model with smaller overall DIC value is preferred.

4. RESULTS FOR THE CASE STUDY

4.1 Selection of Prior Distributions

We analyze the case-control study described in Section 2 using Bayesian methods proposed in Section 3. In this case-control study with J = 3 exposure assessments, only 14 parameters can be estimated. However, for the fully differential and fully dependent misclassification model, 20 independent parameters needed to be estimated. Thus, informative priors are needed for at least 6 parameters such that the full model can be identified. In the following, we will describe the choice of prior distributions for a_eij, b_eij, η_ei and c_eij (e_i = 0, 1, and j = 1, 2, 3) in order.

Firstly, we elicited 95% prior probability intervals for sensitivities and specificities for controls for a_eij (e_i = 0, 1, and j = 1, 2, 3) based on published literature [25-31]. Assuming a normal prior distribution $N({\mu }_{e_{i}j},{\delta }_{e_{i}j}^2)$ for each component of a_eij (e_i = 0, 1, and j = 1, 2, 3), we obtained estimates of μ_eij and ${\delta }_{e_{i}j}^2$ by solving the two equations that set the center value of the elicited 95% probability intervals to be equal to μ_eij, and a quarter of the 95% prior probability interval to be equal to ${\delta }_{e_{i}j}^2$ [21]. The result is presented in Table 2.

Table 2.

Elicited 95% probability intervals for the sensitivities and specificities of the three exposure measurements, and the corresponding prior distributions

		Elicited 95% prior PI	Prior parameters
Next-of-kin respondents	Sensitivity (a11)	0.75-0.98	N (1.36, 0.352)
	Specificity (a01)	0.96-0.99	N(–2.04, 0.152)
Expert assessments	Sensitivity (a12)	0.85-0.99	N(1.68, 0.332)
	Specificity (a02)	0.91-0.98	N(–1.70, 0.182)
Job exposure matrix	Sensitivity (a13)	0.45-0.80	N(0.36, 0.252)
	Specificity (a03)	0.80-0.90	N(–1.06, 0.112)

Note: PI refers to probability interval.

Secondly, vague and independent priors of N(0, 1.1) were assumed for the parameters b_eij (e_i = 0, 1, and j = 1, 2, 3) such that the 95% prior credible intervals for the sensitivities and specificities range from 0.02 to 0.98 for the cases if there is no informative priors for controls. We assumed N(0, 2²) for η₀ and η₁ such that the 95% prior credible intervals for the probability of truly exposed ranges from 0.02 to 0.98, and the corresponding OR ranges from 0.02 to 50. We selected the above non-diffuse (or weakly informative) priors instead of diffuse priors since the latter can lead to inaccurate posterior estimates [32].

Lastly, we discuss the prior choice of c_eij (e_i = 0, 1, and j = 1, 2, 3). The conditional dependence or the positive correlation in either the exposed or the unexposed population arises because of the similarities among multiple measurements, which can be caused by subject-specific characteristics other than the exposure status. These characteristics are summarized by the latent continuous variable Z_i, which varies from subject to subject, and the positive correlations are captured by c_eij (e_i = 0, 1, and j = 1, 2, 3). As c_eij is considered as a scale factor for the standard deviation of the latent continuous variable, it must be positive. An exponential prior distribution of EXP(1) is used for c_eij (e = 0, 1, and j = 1, 2, 3), which corresponds to the standard deviation of the latent continuous variable Z_i ranging from 0.03 to 3.0.

4.2 Summary of Posterior Results

Table 3 presents the posterior medians and the 95% equal tailed credible intervals for 9 models. We can see that ORs estimated from the following 9 models, which consider three assessments simultaneously, are quite different from the ORs from analyses based upon any single assessment. Association estimates obtained by combining results from several mismeasured assessments often will be more accurate than estimates derived from individual assessments because combined results can simultaneously use information from all assessments in a unified manner. Specifically, models 1, 4 and 7 assume nondifferential misclassification (i.e., sensitivities and specificities of exposure classification are the same for cases and controls); models 2, 5, and 8 assume fully differential misclassification (i.e., sensitivities and specificities of the case and control groups are different); and models 3, 6, and 9 assume partially differential misclassification (i.e., only sensitivity of next-of-kin respondents method and sensitivity of job exposure matrix method in the case group are different from the control group). Models 1-3 are the independent models, in which c_eij = 0 (e_i = 0, 1, and j = 1, 2, 3); models 4-6 are the “simplified” or “special” dependent models, in which c_ei1 = c_ei2 = c_ei3 (e_i = 0, 1); models 7-9 are the “general” dependent models, in which c₀₁ ≠ c₀₂ ≠ c₀₃ ≠ c₁₁ ≠ c₁₂ ≠ c₁₃. From Table 3, we see that the “general” dependent models 7-9 show much smaller DIC in general than independent models and “special” dependent models. The model 8, conditionally dependent and differential misclassification model, has the smallest DIC and thus is chosen as our final model. The final model gives a posterior median OR of 15.46 with a 95% credible interval of (7.88, 52.03).

Table 3.

Summary of parameters estimates (posterior median) and their 95% credible intervals

	Conditional independent models			Conditional dependent models (simplified case)			Conditional dependent models (general case)
	1. Nondifferential	2.Differential	3.Partially differential	4. Nondifferential	5.Differential	6.Partially differential	7. Nondifferential	8. Differential	9. Partially differential
Se01	0.66 (0.56, 0.77)	0.34 (0.25, 0.45)	0.35 (0.26, 0.45)	0.83 (0.72, 0.97)	0.36 (0.22,0.69)	0.49 (0.16,0.98)	0.79 (0.65,0.91)	0.74 (0.59,0.93)	0.57 (0.20,0.98)
Se11		0.76 (0.66, 0.88)	0.76 (0.67, 0.83)		0.75 (0.64,0.94)	0.80 (0.68,0.96)		0.81 (0.61,0.97)	0.80 (0.65,0.96)
Sp01	0.98 (0.97, 0.99)	0.98 (0.97, 0.99)	0.98 (0.97, 0.99)	0.94 (0.91, 0.97)	0.97 (0.94,0.99)	0.94 (0.89,0.98)	0.98 (0.95,0.99)	0.98 (0.95,0.99)	0.96 (0.90,0.99)
Sp11		0.99 (0.92,1)			0.99 (0.89,1.00)			0.99 (0.88,1.00)
Se02	0.98 (0.95, 0.99)	0.95 (0.89, 0.99)	0.97 (0.95, 0.99)	0.99 (0.95, 1.00)	0.93 (0.83,0.98)	0.99 (0.94,1.00)	0.96 (0.87,0.99)	0.91 (0.72,0.98)	0.97 (0.90,1.00)
Se12		1.00 (0.97,1)			0.99 (0.93,1,00)			0.99 (0.84,1.00)	0.99 (0.90,1.00)
Sp02	0.68 (0.62, 0.74)	0.75 (0.69, 0.84)	0.75 (0.69, 0.83)	0.58 (0.53, 0.63)	0.72 (0.60,0.83)	0.60 (0.53,0.81)	0.62 (0.58,0.67)	0.62 (0.58,0.66)	0.62 (0.54,0.87)
Sp12		0.74 (0.51, 0.99)			0.74 (0.41,0.99)			0.60 (0.47,0.76)
Se03	0.65 (0.59, 0.71)	0.69 (0.58, 0.80)	0.70 (0.59, 0.80)	0.59 (0.50, 0.68)	0.63 (0.51,0.75)	0.63 (0.35,0.85)	0.60 (0.52,0.68)	0.67 (0.53,0.79)	0.63 (0.43,0.83)
Se13		0.58 (0.50, 0.67)	0.59 (0.50, 0.67)		0.56 (0.48, 0.64)	0.56 (0.47,0.66)		0.55 (0.45,0.65)	0.56 (0.47,0.65)
SP03	0.82 (0.78, 0.86)	0.86 (0.83, 0.89)	0.86 (0.82, 0.89)	0.73 (0.69, 0.77)	0.83 (0.76, 0.88)	0.74 (0.68,0.84)	0.77 (0.73,0.80)	0.77 (0.74,0.81)	0.75 (0.69,0.85)
Sp13		0.84 (0.71, 0.93)			0.79 (0.65,0.92)			0.72 (0.54,0.94)
OR	11.5 (7.15, 19.04)	6.34 (3.41, 11.78)	6.90 (4.37,11.1)	25.84 (13.51,65.74)	8.49 (3.52, 27.69)	17.34 (5.56,80.53)	17.70 (10.59,35.86)	15.46 (7.88,52.03)	14.34 (4.89,54.47)
DIC	2358.00	2318.40	2318.53	2194.83	2201.24	2173.32	1893	1832	2102

Note: Se_dij and Sp_dij denote the sensitivity and specificity for the d^th group (d_i =1, 0 corresponding cases and controls, respectively) and j^th diagnostic assessment (j=1 next-of-kin respondents, j=2 expert assessment, and j=3 job exposure matrix).

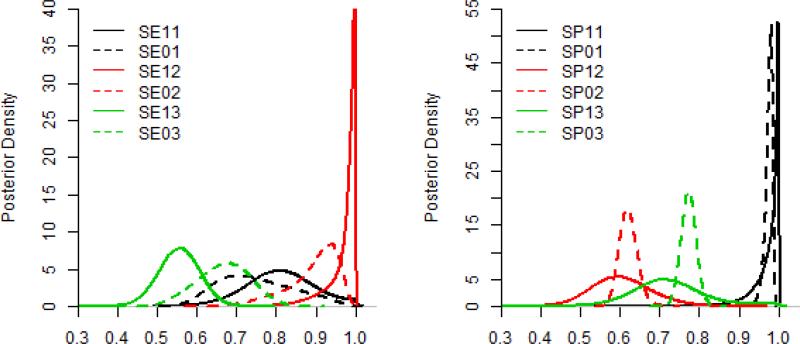
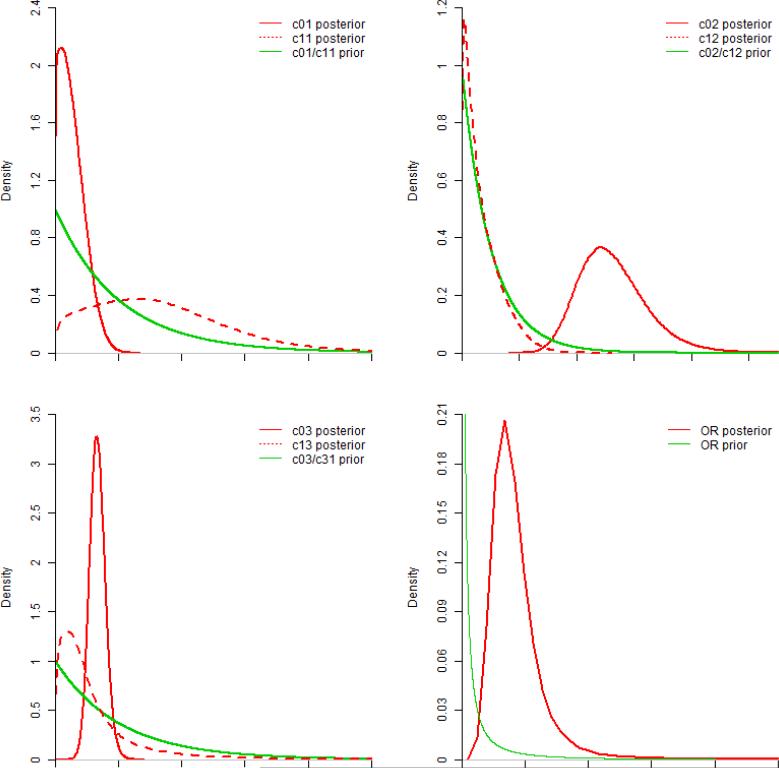
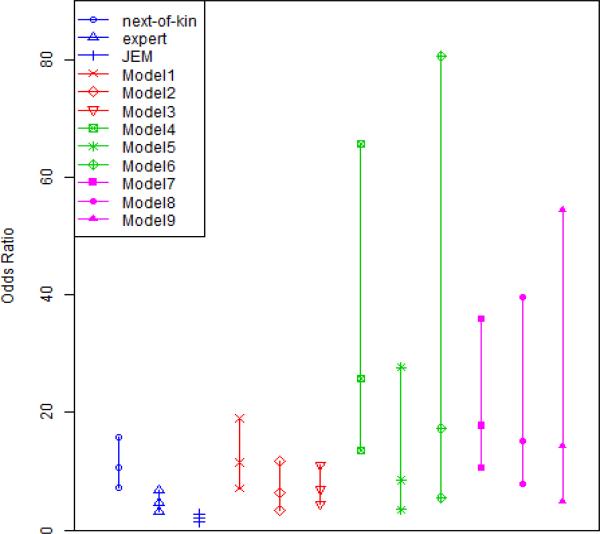
Several figures are plotted in support of our results. Figure 1 shows the posterior distributions of the sensitivities and specificities of three measurements in the final model based on the kernel smoothed density estimation of 50,000 Monte Carlo posterior. Figure 2 displays prior and kernel smoothed posterior distributions of OR, and parameters c_eij. For comparison, Figure 3 shows the medians of OR with 95% credible intervals obtained from our 9 models and individual measurements.

Figure 1.

Posterior Density Distributions of the sensitivities and the specificities of the final model (i.e., model 8 in Table 3). Note: SE11 and SP11 refer to the sensitivity and specificity of the next-of-kin respondents method in the case group respectively; SE01 and SP01 refer to the sensitivity and specificity of the next-of-kin respondents method in the control group respectively. Others are in the same manner.

Figure 2.

Prior and Posterior distributions for c parameters and OR. Note all c parameters have the same exponential prior distribution.

Figure 3.

ORs and 95% Credible Intervals. Model1-Model9 refer to the 9 models in Table 3 (Each vertical line presents the posterior median with 95% credible intervals). Blues lines represent individual measurements; Red lines represent independent models (c_ej = 0); Green lines represent dependent models in the special case (c_eij = c_ei where e_i = 1, 0); purple lines represent dependent models in the general case (c₀₁ ≠ c₀₂ ≠ c₀₃ ≠ c₁₁ ≠ c₁₂ ≠ c₁₃).

4.3 Sensitivity Analysis to Prior Distributions

How sensitive are the posterior results to variations in the priors of c_eij? We approached this question by using several different prior distributions: exponential distribution EXP(1), and the heavy-tailed log-normal distributions LN(0, 1), LN(0, 2²) and Weibull(0.5, 1). The results are presented in Table 4, which shows that the posterior medians and the 95% credible intervals are quite similar using different priors. In summary, for the priors considered, results are consistent.

Table 4.

Sensitivity analyses using different prior distributions

c priors	Exponential (1)	Log-normal (0,1)	Log-normal (0,4)	Weibull (0.5,1)
Se01	0.74 (0.59,0.93)	0.73 (0.58,0.93)	0.72 (0.56,0.94)	0.74 (0.57, 0.95)
Se11	0.81 (0.61,0.97)	0.80 (0.58,0.97)	0.79 (0.57,0.98)	0.81 (0.59,0.99)
Sp01	0.98 (0.95,0.99)	0.97 (0.94,0.99)	0.98 (0.95,0.99)	0.98 (0.95,0.99)
Sp11	0.99 (0.88,1.00)	0.98 (0.84,1.00)	0.99 (0.85,1.00)	0.99 (0.87,1.00)
Se02	0.91 (0.72,0.98)	0.88 (0.68, 0.97)	0.89 (0.66,0.98)	0.91 (0.68,0.98)
Se12	0.99 (0.84,1.00)	0.98 (0.81,1.00)	0.98 (0.80,1.00)	0.99 (0.82,1.00)
Sp02	0.62 (0.58,0.66)	0.60 (0.56,0.65)	0.60 (0.54,0.65)	0.60 (0.55,0.65)
Sp12	0.60 (0.47,0.76)	0.58 (0.47,0.73)	0.58 (0.50,0.73)	0.58 (0.47,0.73)
Se03	0.67 (0.53,0.79)	0.66 (0.52,0.79)	0.67 (0.51,0.79)	0.68 (0.51,0.80)
Se13	0.55 (0.45,0.65)	0.54 (0.44,0.64)	0.55 (0.44,0.66)	0.56 (0.45,0.66)
Sp03	0.77 (0.74,0.81)	0.77 (0.73,0.80)	0.77 (0.73,0.81)	0.77 (0.73,0.81)
Sp13	0.72 (0.54,0.94)	0.70 (0.51,0.95)	0.73 (0.53,0.97)	0.74 (0.55,0.97)
OR	15.46 (7.88,52.03)	16.22 (8.51,89.59)	16.33 (5.53,80.44)	15.32 (8.02,61.49)

5. SIMULATION STUDIES

5.1 Simulated Data and Analysis Methods

Six sets of simulations (labeled as A1, A2, A3, B1, B2, and B3) with different levels of differential/nondifferential misclassification and conditional dependence/independence were performed to evaluate the impact of potential misspecification of misclassification of on the estimation of exposure-disease association. For each set of simulations, 1000 replications were used. Note that while using only 1000 replications leaves some non-negligible simulation error, it was not possible to conduct many more replications given the computational complexity of the Markov chain Monte Carlo method used for the proposed method. To reflect the case study presented in Section 2, 250 cases and 500 controls were generated for each simulated case-control study. Furthermore, the probabilities of true exposure were set to be 0.269 and 0.731 for the controls and cases, respectively, which corresponded to a log odds-ratio of 2.0 for the exposure-disease association.

In set A1-A3, the sensitivities and specificities, i.e., (Se₀₁, Se₁₁, Se₀₂, Se₁₂, Se₀₃, Se₁₃, Sp₀₁, Sp₁₁, Sp₀₂, Sp₁₂, Sp₀₃, Sp₁₃), were set to be conditionally independent with increased levels of differential misclassifications: A1 (0.70, 0.70, 0.90, 0.90, 0.80, 0.80, 0.85, 0.85, 0.80, 0.80, 0.75, 0.75) is nondifferential; A2 (0.80, 0.90, 0.85, 0.95, 0.70, 0.90, 0.85, 0.85, 0.80, 0.80, 0.75, 0.75) is partially differential; A3 (0.80, 0.90, 0.85, 0.95, 0.70, 0.90, 0.85, 0.90, 0.80, 0.90, 0.75, 0.90) is fully differential. In set B1-B3, the sensitivities and the specificities were set to be conditionally dependent with increased levels of differential misclassifications: B1 (0.70, 0.70, 0.90, 0.90, 0.80, 0.80, 0.85, 0.85, 0.80, 0.80, 0.75, 0.75); B2 (0.80, 0.90, 0.85, 0.95, 0.70, 0.90, 0.85, 0.85, 0.80, 0.80, 0.75, 0.75); B3 (0.80, 0.90, 0.85, 0.95, 0.70, 0.90, 0.85, 0.90, 0.80, 0.90, 0.75, 0.90). For the conditionally dependent models, we assumed that they were homogeneously dependent with c_oj = c_1j = 0.5 (j = 1, 2, 3) for simplicity. Of each set, we fit 7 models: 1) an independent non-differential misclassification model; 2) an independent partially differential misclassification model; 3) an independent differential misclassification model; 4) a dependent nondifferential misclassification model where c_oj = c_1j = 0.5; 5) a dependent partially differential model where c_oj = c_1j = 0.5; 6) a dependent differential misclassification model where c_oj = c_1j = 0.5; 7) a dependent differential misclassification model where c₀₁ ≠ c₀₂ ≠ c₀₃ ≠ c₁₁ ≠ c₁₂ ≠ c₁₃.

5.2 Simulation Results Using the Bayesian Approach

We used the same prior distributions as 4.1 for b_eij, c_eij (e_i = 0, 1, and j = 1, 2, 3), η₀ and η₁. But different from 4.1, vague priors N(0, 1.1) were assumed for the parameters a_eij (e_i = 0, 1, and j = 1, 2, 3) such that the 95% prior credible intervals for the sensitivities and specificities range from 0.02 to 0.98 for controls, except that a₁₁ was endowed with informative prior N(0.52, 0.1²) in model 6. Using 20,000 post-burn-in iterations with 10,000 burn-in, Table 5 summarized the posterior medians and the 95% credible intervals of log OR, and also 95% credible interval coverage probability (CICP). It suggests that misspecification of differential/nondifferential misclassification and dependent/independent misclassification can lead to a substantial bias on the estimation of exposure-disease association in an unknown direction when the model is over-specified or under-specified. In addition, a simple simulation is done under the condition that there is no association between exposure and disease. It turns out that our model is robust under this condition and provides less-biased estimates than individual measurements, as is shown in appendix.

Table 5.

Simulation results using Bayesian approach

Settings	Independent			Dependent
Models	A1	A2	A3	B1	B2	B3
Model 1	2.01 (1.59, 2.46)	2.13 (1.73, 2.56)	2.25 (1.84, 2.67)	1.74 (1.34, 2.17)	1.72 (1.32, 2.16)	1.81 (1.53, 2.35)
95% CICP	0.97	0.70	0.72	0.78	0.72	0.78
Model 2	2.02 (1.52, 2.57)	1.96 (1.47, 2.46)	1.70 (1.17, 2.22)	1.65 (1.17, 2.15)	1.80 (1.32, 2.30)	1.52 (1.02, 2.01)
95% CICP	0.97	1.00	0.76	0.77	0.93	0.46
Model 3	1.86 (0.98, 2.71)	1.89 (1.27, 2.49)	1.98 (1.36, 2.54)	1.48 (0.71, 2.24)	1.71 (1.09, 2.34)	1.68 (1.10, 2.25)
95% CICP	0.97	0.95	0.96	0.80	0.88	0.72
Model 4	2.29 (1.70, 3.52)	2.70 (2.13, 3.71)	2.62 (2.04, 3.64)	2.01 (1.55, 3.93)	2.73 (1.98, 4.07)	2.68 (2.02, 3.93)
95% CICP	0.92	0.30	0.41	0.96	0.45	0.44
Model 5	0.54 (-3.08, 3.57)	2.16 (1.02, 3.22)	1.78 (0.73, 2.83)	2.10 (-3.28, 3.86)	2.03 (0.32, 3.76)	1.75 (0.52, 3.18)
95% CICP	0.87	1.00	0.95	0.93	1.00	0.89
Model 6	0.40 (-3.20, 3.47)	1.40 (-0.48, 3.56)	2.04 (0.72, 3.14)	2.02 (-3.84, 3.88)	1.09 (-1.90, 3.62)	1.93 (0.01, 3.43)
95% CICP	0.95	1.00	0.98	1.00	0.96	0.90
Model 7	0.72 (-0.17, 5.71)	0.47 (-0.37,3.72)	1.32 (0.56,5.64)	0.85 (-0.10,6.65)	0.75 (0.02,6.10)	1.18 (0.34,8.21)
95% CICP	0.87	1.00	0.89	0.81	0.80	0.95

Note: This table shows the impact of choosing different misclassification models on the logOR (true value=2) based on simulation studies with 1000 replicates. The three rows for each model correspond to the posterior medians, the 95% credible intervals, and the 95% CICPs (credible interval coverage probabilities) for logOR. The bold cells represent the estimates obtained from the model correctly specified.

5.3 General Guidance for the Practitioners

Misspecification of differential/nondifferential and dependent/independent misclassification can lead to a substantial bias on the estimation of exposure-disease association in an unknown direction when the model is over-specified or under-specified. Thus we suggest fitting all models as is done in Table 3 for the future data analysis and selecting the model with the smallest DIC as the final model.

6. DISCUSSION

In this paper, we proposed a Bayesian approach to show that misspecification of dependent/independent and/or differential/nondifferential misclassification can lead to substantial bias in the estimation of exposure-disease association. In our application presented in Section 4, the measurement error-corrected OR was 15.46 (95% CL: 7.88, 52.03) under dependent and differential misclassification assumption. Our proposed approach can also be used to estimate the accuracy of imperfect measurements and to test whether the misclassification is likely to be differential or non-differential incorporating conditional dependence, when multiple non-gold standard exposure assessments are used in case-control studies.

In the Chu et al. likelihood-based approach [2], a model with full differential and full conditional dependent misclassification was not identifiable with only three error-prone measurements. Thus, they used a somewhat ad hoc approach to select a “final” partial differential and constrained conditional dependent model. Specifically, they first selected a “partially differential independent misclassification model” among the 3 conditional independent models based on a likelihood ratio test. Then, they assumed a homogeneous conditional dependence on specificities to find the final model. However, their approaches may not guarantee the best-fit model due to identifiability issues, e.g., their approach is incapable to consider heterogeneous dependence on sensitivities and specificities (i.e., c₀₁ ≠ c₀₂ ≠ c₀₃ ≠ c₀₄ ≠ c₀₅ ≠ c₀₆) corresponding to model 7-9 in Table 3. With informative priors constructed from the literature, our Bayesian approach overcomes the identifiability issues [21], and can provide an useful alternative in practice.

In this article, we implemented a retrospective logistic regression model to estimate the exposure-disease association by logit(Pr(E_i = 1) = η₀ + η₁D_i as this parameterization facilitates the specification of the distribution of Y|E through a mixture. As shown in Seaman and Richardson[33, 34], for the Bayesian analysis using suitable priors as well as the classical frequentist analysis, with any number of categorical or discretized continuous exposure and confounding variables, the “prospective” likelihood (i.e., the likelihood of disease give exposure), and the “retrospective” likelihood (i.e., the likelihood of exposure given disease) lead to the same odds-ratio estimator. In general, the introduction of a few other categorical covariates or discretized continuous covariates will alleviate the identifiability issue because we will gain more degrees of freedom than the number of additional parameters to estimate. Note that the definition of degrees of freedom here is different from what it is defined in a linear regression with continuous outcome, where it is determined by the sample size and number of parameters and will be decreased by adjusting additional covariates. However, in the categorical data analysis, the total degrees of freedom equals the number of populations times the number of categories minus 1. Suppose J diagnostic tests are applied simultaneously to individuals drawn independently from M populations, the total degrees of freedom in the data is M(2^J –1)[15]. If there is only one binary covariate D, the number of populations M equals to 2 and thus the total degree of freedom equals 2×(2^J –1). If there are P binary covariates in addition to D to be adjusted, the degrees of freedom will be enlarged to 2^P+1×(2^J –1). Of course, one cannot increase degrees of freedom to be larger than the sample size by adding covariates. On the other hand, the number of additional parameters to estimate equals to the number of additional covariates if we assume the error-prone exposure measurements do not depend on the additional covariates given the true underlying exposure and disease status (corresponding to formula 3.1), which is quite reasonable in practice. In general, the identifiability issue is alleviated by adding additional covariates. One drawback of our approach is that we only considered a binary status for both the underlying true exposure and the error-prone exposure measurements. Extending the proposed methods to categorical exposures should be straight forward, e.g., by using a generalized logit model to model P(E|D) and P(Y|D, E). However, it may be difficult in practice to solicit informative priors for the misclassification parameters. This extension as well as ordinal exposures awaits further development.

In summary, misclassification of exposure status is very common in case-control studies. Estimates obtained by combining multiple exposure assessments are more accurate than estimates derived from a single individual exposure assessment. Misspecification of differential/nondifferential misclassification and conditional dependence/independence can lead to noticeable bias in exposure-disease association in an unpredictable direction. Thus careful attention should be paid to competing misclassification models when conducting analysis involving multiple error-prone exposure measurements in case-control studies.

Appendix

Appendix.

We generated data with no association between the exposures and the disease. More specifically, we let the probabilities of being exposed in both case and control to be 0.4, thus the OR of exposure comparing cases and controls are 1. Sensitivities are set to be 0.60, 0.65, and 0.55 for controls; while 0.65, 0.70, and 0.60 for cases. Specificities are set to be 0.85, 0.80, and 0.75 for controls; while 0.90, 0.90, and 0.90 for cases. The following results show that our approach provided less-biased estimate than individual measurements.

True OR	Our method OR	Next-of-kin OR	Expert OR	JEM OR
1.00	1.05	0.95	0.85	0.73