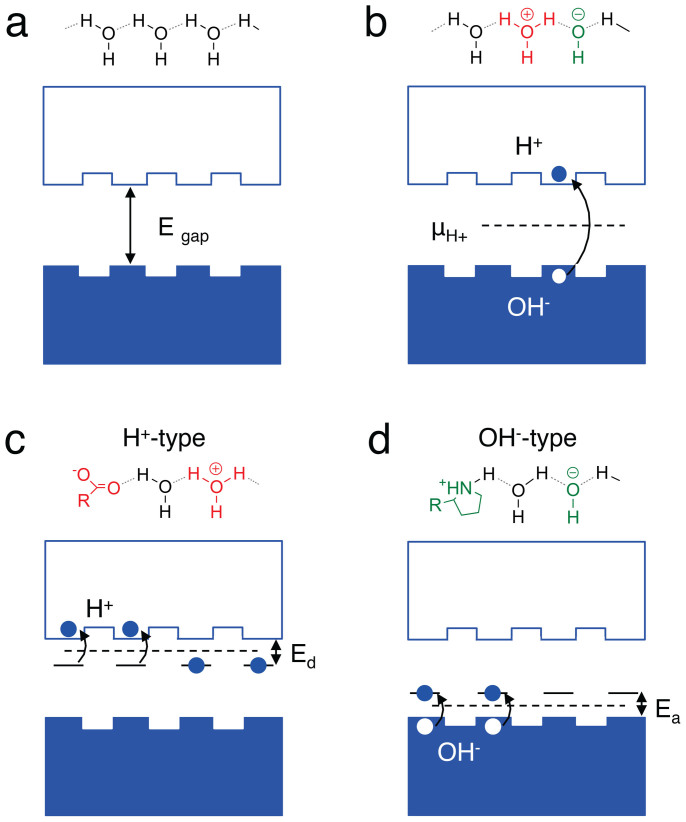
Figure 2. Energy diagram representation of conduction in hydrogen bonded proton wire.

(a) A wire with no H⁺ or OH⁻ defect does not conduct. The band gap is defined as the energy required to create a H⁺ OH⁻ pair (proton-proton hole) and is derived from the E_gap = ΔG⁰′ = −k_BT ln K_w = 0.83 eV (Gibbs-Helmholtz equation). (b) For an intrinsic proton wire, the protochemical potential u_H+ is in the middle of the band-gap. The H⁺ is not completely delocalized along the conduction quasi band. Hopping barriers of approximately 100 meV (need to be overcome for conduction to occur. (c) An acid donates a H⁺ into the conduction band of a proton wire to yield a H⁺-type protonic conductor. E_d = ΔG⁰_a = −k_BT ln K_a, K_a is the acid dissociation constant. The maleic acid group pK_a (-log K_a) = 3.2, which corresponds to E_d = 0.18 eV. (d) A base accepts a H⁺ to create a OH⁻ (proton hole) in the valence band of a proton wire to yield a OH⁻-type protonic conductor. E_a = ΔG⁰_b = −k_BT ln K_b, K_b is the base dissociation constant. The proline base pk_b (-log K_b = 3.4), which corresponds to E_a = 0.20 eV. For both H⁺ type and OH⁻ type the protochemical potential is μ_C^H+ = eV₀ + µ₀+ k_BT ln a_H+ where a_H+ is the activity of H⁺.