Fig. 2.

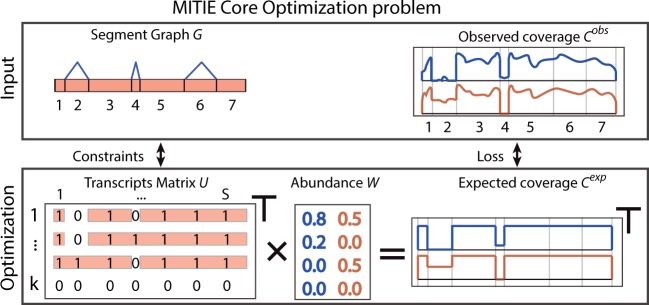
Illustration of the core optimization problem of MITIE. The transcript matrix U (bottom left) and abundance matrix W (bottom center) will be optimized such that the implied expected read coverage of the k valid transcripts (bottom right) matches the observed coverage (top right) well. Validity of the transcripts is ensured by appropriate constraints derived from the segment graph (top left). We illustrate the case of two samples. For each sample, we have abundance estimates W for each of the k = 4 transcripts. The identity of the transcripts, i.e., the rows of U, is shared among the samples. By Occam’s razor principle, we implement a trade-off between loss between the observed and expected coverages and the number of used transcripts, i.e. number of rows in W with non-zero abundances