Systems-level Modeling with Molecular Resolution Elucidates the Rate-limiting Mechanisms of Cellulose Decomposition by Cellobiohydrolases

Background: Cellobiohydrolase enzymes processively degrade crystalline cellulose into free sugar molecules.

Results: A spatially resolved kinetic model has been developed to understand the effects of interfacial confinement on cellobiohydrolase activity.

Conclusion: Cellobiohydrolase activity is limited by slow rates of complexation with cellulose and traffic jamming among enzymes on the substrate.

Significance: Identifying kinetic effects imposed by interfacial confinement is crucial for understanding and engineering cellulose bioconversion.

Abstract

Interprotein and enzyme-substrate couplings in interfacial biocatalysis induce spatial correlations beyond the capabilities of classical mass-action principles in modeling reaction kinetics. To understand the impact of spatial constraints on enzyme kinetics, we developed a computational scheme to simulate the reaction network of enzymes with the structures of individual proteins and substrate molecules explicitly resolved in the three-dimensional space. This methodology was applied to elucidate the rate-limiting mechanisms of crystalline cellulose decomposition by cellobiohydrolases. We illustrate that the primary bottlenecks are slow complexation of glucan chains into the enzyme active site and excessive enzyme jamming along the crowded substrate. Jamming could be alleviated by increasing the decomplexation rate constant but at the expense of reduced processivity. We demonstrate that enhancing the apparent reaction rate required a subtle balance between accelerating the complexation driving force and simultaneously avoiding enzyme jamming. Via a spatiotemporal systems analysis, we developed a unified mechanistic framework that delineates the experimental conditions under which different sets of rate-limiting behaviors emerge. We found that optimization of the complexation-exchange kinetics is critical for overcoming the barriers imposed by interfacial confinement and accelerating the apparent rate of enzymatic cellulose decomposition.

Introduction

Unraveling enzyme kinetics under interfacial confinement is a core problem of in vivo biology (1). Progress in this task is severely restrained by the limitation in resolving protein behaviors and their effects on biochemical reactions in heterogeneous environments. Here, we overcame this issue for a very important biocatalyst in the decomposition of cellulose (2–5). The enzyme system of our investigation is the most abundant cellobiohydrolase produced by the Trichoderma reesei fungus, TrCel7A² (6). We devised a novel systems-level simulation method that incorporates molecular scale spatial resolution to illuminate the non-classical behaviors in enzyme kinetics due to surface restriction. The capabilities we established for tracking single-enzyme movements during the course of the biochemical reaction allow clear elucidation of the molecular origins that limit the apparent rate of substrate conversion. A comprehensive understanding of the interfacial biocatalysis of TrCel7A can help to identify effective engineering strategies for improving the technologies of cellulose bioconversion (7, 8).

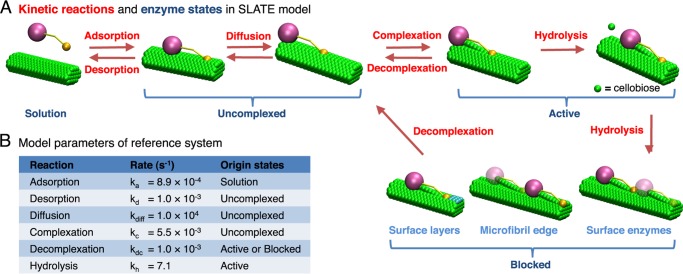
The elementary kinetic reactions performed by TrCel7A are shown in Fig. 1A (4, 9). The enzymes adsorb onto crystalline cellulose microfibrils that are composed of linear glucan chains held tightly together by hydrogen bonding and van der Waals interactions (3). On the microfibril surface, an adsorbed enzyme diffuses until it complexes with the free reducing end of a glucan chain (6). Complexation involves extraction of the targeted chain from the surface and threading of the linear polymer into the active site tunnel of TrCel7A (6). Once complexed, the enzyme can processively hydrolyze the β1,4-glycosidic linkages within the captured chain and release a cellobiose molecule into solution after each bond cleavage. The consecutive hydrolysis along a single chain stops when the enzyme decomplexes or becomes blocked by surface obstacles (10–12).

FIGURE 1.

Illustration of the SLATE model for TrCel7A. A, kinetic reactions (labeled in red) and enzyme states (labeled in blue) in the SLATE model. Cellulase enzymes can participate in one of the following reactions: adsorption, desorption, diffusion, complexation, decomplexation, and hydrolysis. Only hydrolysis is treated as an irreversible reaction. With these reaction steps, an enzyme can be in one of the four states: solution, uncomplexed, active, and blocked. These states are mutually exclusive and completely exhaustive. A blocked enzyme can be stalled by uneven surface layers, the nonreducing edge of the microfibril substrate, or the other surface enzymes. B, kinetic rates for the reference system. The possible originating states for each reaction is shown under Origin states.

In interfacial biocatalysis, the heterogeneous and crowded environments around insoluble substrates can induce complex protein-protein and protein-biomaterial couplings that are difficult to characterize (9, 13). For example, the rate constants of the complexation-exchange of TrCel7A (4, 9) have not been measured as stand-alone steps. Furthermore, as a result of the excluded volume constraints, the displacement of processive TrCel7A enzymes is sensitive to obstacles on the microfibril surface that can cause “traffic jams” of proteins (9–12). Similar issues due to confinement on an extended molecular surface can be found in other systems like motor proteins (14). In such scenarios, the classical mass-action principles that assume a dilute and well mixed reaction medium become inappropriate (9, 13). For the case of cellulose decomposition by TrCel7A, we illustrate that spatiotemporal resolution of the enzyme kinetics is essential for uncovering the rate-limiting mechanisms.

EXPERIMENTAL PROCEDURES

Stochastic Lattice Enzyme (SLATE) Model

To understand the effect of spatial confinement on cellulase kinetics, we developed a lattice kinetic Monte Carlo (kMC) model to simulate the elementary kinetic reactions (see Fig. 1A) of individual cellulases on cellulose microfibrils with a molecular scale spatial resolution. The SLATE model developed here describes the spatiotemporal enzyme reaction network in three dimensions and explicitly tracks the locations of individual enzymes and cellobiose residues. As illustrated in Fig. 1A, each TrCel7A enzyme in the model can perform the following reactions: adsorption, desorption, diffusion, complexation, decomplexation, and hydrolysis.

The shapes and sizes of individual TrCel7A enzymes (15, 16) and microfibril glucan chains were resolved onto a three-dimensional lattice with 5-Å cubic grid cells as shown in Fig. 1A and supplemental Fig. S1. This grid size allowed explicit representation of each glucose residue in the glucan chains of a microfibril (17, 18). Excluded volume constraints were imposed between molecules in the system by enforcing that any two entities could not have common lattice sites. The geometry and elementary steps of the system are further described in the supplemental data.

According to the structural features of plant cellulose, the simulation model of the microfibril consists of 36 glucan chains (17) with a degree of polymerization of 1024 glucose residues (2) (see supplemental Fig. S1). Formation of the enzyme-substrate complex via the complexation step occurs only at the reducing end of glucan chains due to the specificity of TrCel7A (6). The average number of TrCel7A enzymes adsorbed on the microfibril is 18. This loading corresponds to a cellulose surface coverage of 25%, which is within the typical range employed in experiments (19).

Kinetic Rate Constants of Elementary Reactions

The kMC model requires rate constant data to perform stochastic simulations of the enzyme reaction network. For the steps that have been characterized experimentally, the values employed in the simulation model are shown in Fig. 1B. For the complexation rate constant that is unavailable, the value was calibrated by reproducing the conversion versus time profile of decomposing Avicel by TrCel7A measured by Gusakov et al. (20). Details of the rate constants employed in the simulation model are described below.

Via this calibration procedure, the desorption rate constant of TrCel7A was estimated to be in the range 1 × 10⁻³ to 1 × 10⁻² s⁻¹, consistent with the values inferred from the bulk measurements of reaction kinetics (21–24). The reference value of the complexation rate constant employed in our SLATE simulations was set to 1 × 10⁻³ s⁻¹; using the value of 1 × 10⁻² s⁻¹ does not alter the resulting conversion profiles by >5%.

Next, the adsorption rate constant could be determined by the equilibrium adsorption constant K and system volume V. For TrCel7A adsorbing on Avicel, a representative value for K is 0.28 liters/μmol (2, 25). The volume of the simulation model was then set by ensuring that the cellulose concentration in the system is the same as the concentration used by Gusakov et al. (20), 5 mg/ml. With the values of K and V, the adsorption rate constant was calculated by converting the phenomenological bimolecular adsorption rate of k_dK to a first-order association rate constant (26) as k_a = k_dK/(VN_AV10⁻⁶) = 8.9 × 10⁻⁴ s⁻¹. The factor of N_AV10⁻⁶ was used to convert μmol in K to number of molecules, and N_AV is Avogadro's number.

The surface diffusion rate constant is related to the self-diffusion coefficient D_S from random walk theory as k_diff = 4D_S/l_h², where l_h = 1 nm is the hopping distance (27). With the experimentally measured diffusion constant of 1 × 10⁻¹⁰ cm²/s (28), the resulting diffusion rate constant is 1 × 10⁴ s⁻¹.

The hydrolysis rate was determined from the processive speed of TrCel7A of 7.1 nm/s (12). Because a cellobiose unit is ∼1 nm long, the corresponding hydrolysis rate was thus set to 7.1 s⁻¹. The decomplexation rate constant was estimated to be ∼1 × 10⁻³ to 1 × 10⁻² s⁻¹ from bulk kinetic measurements (29–32). In some studies (30–32), this rate is lumped together with desorption. The reference value for the SLATE model was set to be 1 × 10⁻³ s⁻¹ and was extensively varied in different simulations to account for the uncertainty.

As mentioned above, the complexation rate constant is difficult to measure directly. A common idea obtained based on the inference from indirect kinetic data is that the value is much lower than that of the hydrolysis reaction (29, 33, 34). Another feature of the reference conversion profile (20) that we employed for calibrating the complexation rate constant is a rapid decline with time. Therefore, we employed two complexation rate constants in the SLATE model to quantitatively capture this behavior. In the initial microfibril at the start of a SLATE simulation, we assumed that the glucan chains in the solvent-exposed surfaces of the top and bottom layers are more loosely packed. The complexation rate constant of TrCel7A with the glucan chains on these surfaces was thus set to be 10 times faster than that of complexation with the originally buried chains. Recalcitrance of cellulose toward enzymatic decomposition would then increase with time in the SLATE simulation, leading to rapid retardation in the apparent reaction rate (9). With a single microfibril in the simulation model, this treatment also builds in structural heterogeneity in the material effectively (2, 9). The best fit values for the fast and slow complexation rates are 5.5 × 10⁻³ and 5.5 × 10⁻⁴ s⁻¹, respectively. In the main text, the faster value is referenced and shown in Fig. 1B. The mechanistic trends and rate-limiting behaviors identified in this work do not depend on whether one or two complexation rate constants were used (data not shown).

Moreover, in the reference kinetic data (20) used to calibrate the complexation rate constant, the substrate is Avicel, which is composed of aggregated microfibrils. In contrast, the simulation model contains a single microfibril and hence overestimates the solvent-exposed surface area, i.e. 293 versus 2.38 m²/g (35). As a result, by using an enzyme surface coverage within the experimental range (19), the enzyme/substrate mass ratio in the SLATE model is thus higher than those in experiments. To investigate the potential impact on underestimating the complexation rate constant with a higher enzyme loading, we performed simulations at lower enzyme loadings and estimated that a 100-fold reduction would yield a best fit complexation rate constant ∼0.1 s⁻¹. As this value is still >2 orders of magnitude lower than the rate constant of hydrolysis, the result of complexation as the rate-limiting step does not depend on using surface coverage or enzyme loading as the basis to calibrate the simulation model. Because enzymatic cellulose decomposition is an interfacial process, we opted to use surface coverage instead of enzyme loading to connect with experimental results quantitatively.

Lattice kMC Scheme with Molecular Resolution

The simulation engine of the three-dimensional SLATE model for enzymatic cellulose decomposition is a lattice kMC scheme (36). This algorithm was used to simulate the elementary kinetic reactions listed in Fig. 1A for all enzymes in the system.

kMC-based simulation models have been used to represent the kinetics of surface phenomena in many areas such as heterogeneous catalysis (36) and motor protein transport (14). Because enzymatic cellulose decomposition occurs at material surfaces, we adopted kMC to model this process. The kMC framework was also adopted here to eliminate the limitations of kinetic modeling of enzymatic cellulose conversion. In this regard, key assumptions of elementary steps such as the complexation and decomplexation steps occurring instantaneously are often imposed without careful justification (37). The commonly employed strategies of reducing dimensionality and combining steps such as adsorption and diffusion (38) would then leave out molecular details on different levels. Therefore, cross-comparison of the results of different simulation models and their usage for quantitative reproduction of the measured conversion profiles are difficult.

In this work, we aimed to overcome these difficulties by incorporating a full suite of spatiotemporal behaviors in the three-dimensional space in SLATE. The high resolution of the 5 Å lattice size can capture the evolving microfibril structures that couple to enzyme kinetics during cellulose decomposition. To the best of our knowledge, SLATE is the first of its kind that simultaneously accounts for the molecular structures of the enzymes and substrates in the three-dimensional space, the full kinetics of complexation-exchange, enzyme processivity, and jamming formation in modeling enzymatic cellulose decomposition.

To simulate the reaction kinetics of cellulose decomposition, the null-event kMC algorithm, described further in the supplemental data, was used (36). A significant increase in computational speed was achieved by treating diffusion via a stochastic quasi-equilibrium approximation (39) that is characterized and justified in the supplemental data. With this method, a 50-fold increase in computational speed could be achieved. Conversion profiles up to 200 h of reaction time could be simulated in <5 h on a single CPU. In this work, the reported quantities were averaged over a sufficient number of independent trajectories for the statistical uncertainties to become negligible.

Analysis of Single-enzyme Kinetics

A key feature of the SLATE model is the ability to track the states of individual enzymes. As shown in Fig. 1A, a TrCel7A enzyme can be in one of four states: 1) in solution, 2) uncomplexed, 3) active, and 4) blocked. Once complexed, a TrCel7A molecule is either active or blocked. An active enzyme can perform hydrolysis or decomplex, whereas a blocked enzyme can only decomplex. The obstacles on the microfibril surface include (a) uneven surface layers, (b) the nonreducing edge of the microfibril, and (c) the other surface enzymes. An illustration of each type of obstacle is shown in Fig. 1A. The nonreducing edge of the microfibril substrate prevents TrCel7A enzymes from passing over due to the high affinity of the carbohydrate-binding domain of TrCel7A for crystalline cellulose (40, 41). Effectively, this block also represents restrictions due to immobile structural obstructions such as hemicellulose and lignin (11). Under “Results,” we analyze the duration of time that an enzyme spends in each of these states to quantify the kinetic bottlenecks and relate them to enzyme activity.

RESULTS

Surface Enzymes Are Mostly Inactive Due to Slow Complexation and Excessive Blocking

In Fig. 2A, snapshots from a SLATE simulation illustrate the gradual erosion of the microfibril substrate by TrCel7A. Because the processive cellulase decomposes glucan chains starting from their reducing ends (6), a more drastic thinning of the reducing edge develops with time as observed in experiments (42–44). Quantitative agreement between the simulated and experimentally measured conversion (20) profiles is illustrated in Fig. 2B.

FIGURE 2.

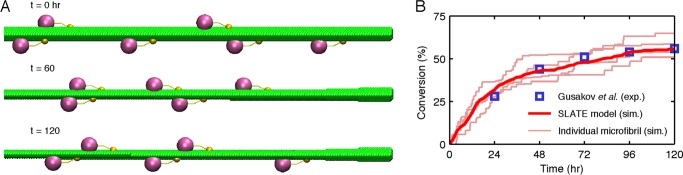
Illustration of kMC simulations with the SLATE model. A, snapshots from a simulated trajectory showing the degradation of a microfibril substrate over time. Only one-quarter of the microfibril length in the model is shown; the nonreducing edge is located on the right side. The processing TrCel7A enzymes move from left to right after adsorbing onto the hydrophobic (top and bottom) faces of the microfibril (41). B, the averaged substrate conversion over time in a SLATE simulation (dark red line) and the conversion from the study of Gusakov et al. (20) (blue squares) on the decomposition of Avicel by TrCel7A. The conversion profile (dark red line) from averaging over eight independent simulations quantitatively agrees with the experimental data (exp.). Each simulation (sim.) represents the decomposition of an individual microfibril. Four of the eight simulations involved in the average are also shown for comparison as light red lines. The parameters used in SLATE simulation are listed in Fig. 1B.

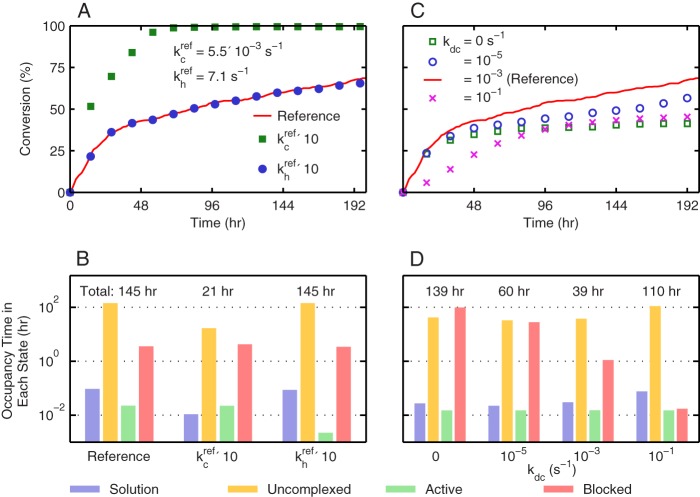
Fig. 2B also shows that the conversion profiles of several individual microfibrils exhibit substantial deviation from one another and from the averaged profile. One signature of single-microfibril kinetics that becomes obscured by averaging over multiple trajectories is the pattern of flat regions linked together by steep jumps. The extensive flat periods reflect long waiting times for uncomplexed enzymes to become active and are indicative of complexation-limited kinetics. Increasing the complexation rate constant by 10-fold over the reference rate constant drastically enhanced the conversion of cellulose decomposition in Fig. 3A, but the same increase in the hydrolysis rate constant hardly resulted in any change in the profile.

FIGURE 3.

Effects of using different values of kinetic rate constants in SLATE simulations for the illustration of rate-limiting mechanisms. A, profile of the averaged substrate conversion over time using the reference parameters shown Fig. 1B (red line), a 10-fold higher value for the complexation rate constant k_c while keeping others unchanged (green squares), and a 10-fold higher value for the hydrolysis rate constant k_h while keeping others unchanged (blue circles). B, distributions of enzyme occupancy times in the following four states: solution (violet), uncomplexed (yellow), active (green), and blocked (red). Surface obstacles causing the blocked state include uneven surface layers, the nonreducing edge of the microfibril, and the other surface enzymes. The values shown above the bars are the total reaction times to reach 60% conversion. These values are the sum of the occupancy times over all of the four enzyme states. C, averaged profiles of substrate conversion over time using the reference parameters of Fig. 1B (red line) and varying the decomplexation rate constant k_dc from 0 to 10⁻¹ s⁻¹ while keeping others unchanged (symbols). D, distributions of enzyme occupancy times in the four states listed in B as a result of varying the decomplexation rate constant while keeping the others unchanged. The total reaction times above the bars represent the times to reach 40% conversion. For all of the data presented, the standard deviations are not shown for clarity, and they are within 5% of the averaged values.

To quantitatively dissect the kinetic bottlenecks of cellulose conversion at the single-molecule level, the duration that an enzyme spends in each state (Fig. 1A) during the reaction was recorded to determine the enzyme occupancy times in different states; further details of this calculation are described in the supplemental data. States with a high occupancy time signal the kinetic traps that prevent TrCel7A enzymes from becoming active. Fig. 3B plots the occupancy time distribution of the reference simulation and those from increasing the complexation or hydrolysis rate constant by 10-fold over the reference value. The total reaction time (sum of the occupancy times of all states) labeled above the bars in Fig. 3B is the duration to reach 60% conversion. The uncomplexed state clearly has the longest occupancy time in all cases. Fig. 3B also shows that a 10-fold higher complexation rate constant reduced the uncomplexed occupancy time by tens of hours. The same increase in the hydrolysis rate constant only reduced the active state time by tens of seconds.

By resolving the decomposition of cellulose at the single-enzyme level, SLATE simulations identify that a major cause for the TrCel7A enzymes to be predominantly inactive on the substrate surface is the slowness of extracting glucan chains from microfibrils and threading them into the active site tunnel. This finding is consistent with those of several reports that were inferred from bulk measurements (33, 34). The SLATE-computed complexation time scale on the order of hours is also in agreement with recent experimental findings (29). The observed rate-limiting complexation behavior is robust to assumptions made in the kinetic model, as further discussed in the supplemental data.

A striking message in Fig. 3B is that even after overcoming the kinetic barrier to reach the complexed state, the enzymes spend >99% of their time blocked without performing hydrolysis. Therefore, along with the high free energy barrier in the complexation step, the excessive blocking experienced by enzymes on the surface makes the active state of TrCel7A short-lived. The stalling of TrCel7A molecules on a cellulose microfibril has been inferred from solution-phase “restart” experiments (10, 11) and transiently observed via high speed atomic force microscopy (12). As illustrated below, acceleration of cellulose conversion can be achieved most effectively by increasing the complexation rate with coordinated removal of enzyme blocking.

Decomplexation Plays Opposite Roles in Affecting Productivity

Decomplexation is the required step for a blocked enzyme to escape an obstacle. Fig. 3C plots the different conversion profiles from using various values for the decomplexation rate constant k_dc in SLATE simulations while fixing the other rate constants at their reference values. It can be seen that a maximum in conversion occurs at the reference value of 1 × 10⁻³ s⁻¹ that was inferred from bulk experiments (29–32). The occupancy time distributions at 40% conversion in Fig. 3D illustrate the two opposing forces introduced by increasing k_dc. A higher decomplexation rate reduces the occupancy of the blocked state but also decreases the thermodynamic driving force (k_c/k_dc) of complexation.

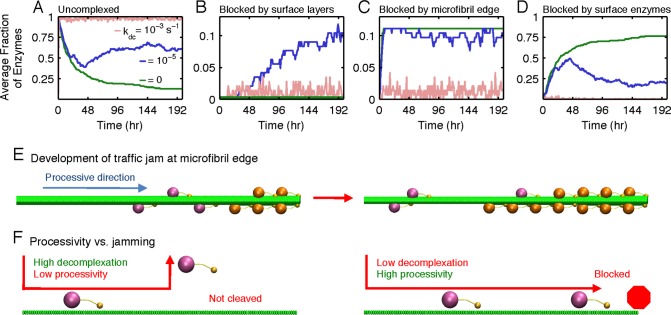
To further illustrate the conversion maximum resulting from the two competing effects of decomplexation, the fractions of TrCel7A enzymes in each state were tracked over time during the simulated courses of cellulose decomposition at different k_dc values. Fig. 4A indicates that at the reference k_dc of 1 × 10⁻³ s⁻¹, a large fraction (∼95%) of surface enzymes are uncomplexed due to the low complexation rate. Decreasing the k_dc from this value lowers the uncomplexed fraction but raises the fraction of enzymes in blocked states. This increase compensates the effect of having a higher complexation driving force for the enzymes to be more active (Fig. 4, B–D). To reveal the molecular origins of these competing trends, the detailed mechanism of enzyme blocking on the microfibril substrate was analyzed next.

FIGURE 4.

Fraction of each surface enzyme spent in different states over time if the decomplexation rate constant k_dc (s⁻¹) is 0 (green), 10⁻⁵ (blue), and 10⁻³ (light red) while the other rate constants remain at the reference values of Fig. 1B. A, profiles of the fraction of uncomplexed enzymes. B, profiles of the fraction of enzymes blocked by uneven surface layers of glucan chains on the microfibril surface. C, profiles of the fraction of enzymes blocked by the nonreducing edge of the microfibril. D, profiles of the fraction of enzymes blocked by the other enzymes on the substrate surface. E, illustration of a traffic jam developed at the nonreducing edge of the microfibril (right side) when the decomplexation rate constant is low. Blocked enzymes are colored in orange. Only one-quarter of the microfibril length is plotted with the nonreducing edge located on the right side. F, illustration of the interplay between enzyme blocking and processivity in affecting the reactivity of cellulose decomposition. A less processive enzyme tends to decomplex prematurely, and the glycosidic bonds near the nonreducing ends of glucan chains in the substrate cannot be cleaved effectively. An overly processive enzyme cleaves the entire glucan chain after each complexation event but decomplexes very slowly and tends to be blocked at the nonreducing edge.

The fraction of surface layer-blocked enzymes is plotted in Fig. 4B. When k_dc is zero, this fraction is also zero because the surface is initially smooth, and the TrCel7A enzymes cannot decomplex to make uneven surface layers. When k_dc = 1 × 10⁻⁵ s⁻¹, uneven steps start to form on the surface to block enzymes. Because escaping from the surface layer obstacles requires tens of hours due to the slow rate of decomplexation, a large fraction of surface layer-blocked enzymes develops. As k_dc is raised to 1 × 10⁻³ s⁻¹, the fraction becomes low because enzymes can decomplex within minutes after encountering these obstacles.

The edge-blocked fractions of TrCel7A during decomposition are shown in Fig. 4C. When k_dc is below 1 × 10⁻³ s⁻¹, a steady occupancy of this state is observed because once the enzymes become complexed, they likely process all the way to the nonreducing edge without decomplexation due to the low value of k_dc. The edge-blocked enzymes then nucleate other lagging enzymes to become blocked and form the head of the traffic jam. The lagging proteins in the traffic jam are in the enzyme-blocked state, the fractions of which are shown in Fig. 4D. The traffic jam buildup on the microfibril is illustrated in Fig. 4E. With the nonreducing edge effectively playing the role of an immobile obstacle, the blocked enzymes are mostly stuck in traffic instead of being stalled by uneven surface layers.

The optimal k_dc value of 1 × 10⁻³ s⁻¹, at which the conversion in Fig. 3C reaches a maximum, represents the ideal balance in maintaining enzyme processivity while reducing the fraction of enzyme jamming on the cellulose surface. Fig. 4F shows that if k_dc assumed a higher value, the TrCel7A molecules would decomplex prematurely and fail to hydrolyze the glycosidic bonds near the nonreducing edge of the microfibril after each complexation event. The optimal k_dc thus needs to be sufficiently high for the surface enzymes to be free from jamming but adequately low for them to be as processive as possible. In this case, the complexation time scale is commensurate with the average duration for the enzyme to process through a glucan chain on cellulose. In addition to this signature in the time scale, the optimal k_dc can also be characterized via the apparent processivity, the average number of bonds cleaved per complexation event, L_p (30). Figs. 5A and 3C show that the optimal k_dc corresponds to the value at which L_p begins to level off with respect to a further increase of the complexation driving force from reducing k_dc.

FIGURE 5.

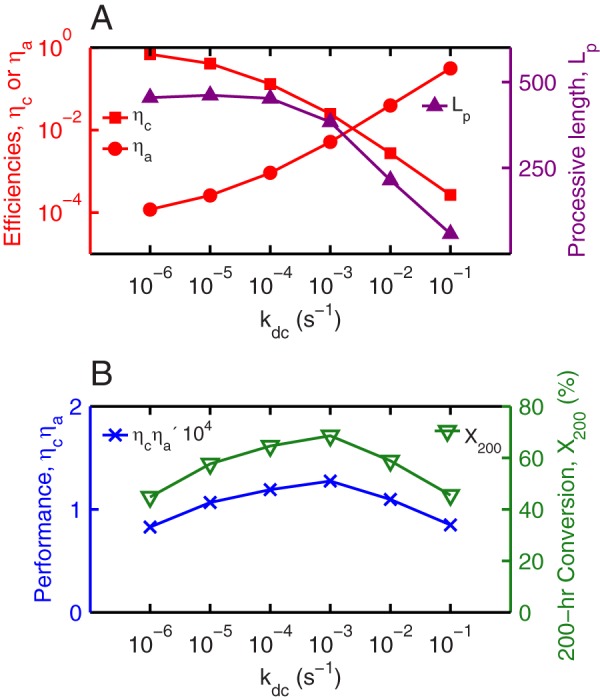
Efficiency measures, processive length, performance, and apparent activity of TrCel7A in cellulose decomposition as a function of the decomplexation rate constant k_dc. A, profiles of the complexation and activation efficiencies, η_C and η_A, respectively (red), and processive length, L_p (purple). The maximal processive length is 512, which is set by the averaged degree of polymerization of 1024 glucose residues per glucan chain. B, profiles of performance (blue) and 200-h conversion (green).

Kinetic Efficiencies of Enzymes Quantify the Performance of Interfacial Biocatalysts

The significant impact of TrCel7A jamming on the apparent kinetics of cellulose decomposition motivates the development of efficiency measures to characterize the enzyme performance during interfacial biocatalysis. The ratio of complexed to surface enzymes is the complexation efficiency, η_C, and the ratio of active to complexed enzymes is the activation efficiency, η_A. As such, η_C measures the intrinsic enzyme activity for complexation, whereas the effects of the structural heterogeneity of the substrate surface, interenzyme blocking, and enzyme-obstacle exclusion on kinetics are lumped into η_A. Fig. 5A plots η_C and η_A as a function of k_dc for a 200-h decomposition, and their dependences on the decomplexation rate constant are clearly opposite as discussed above. η_C also has a close correspondence with L_p.

The overall conversion can be quantitatively related to the efficiencies through a performance metric. As derived in the supplemental data, the conversion X_T after reaction time T is proportional to the enzyme performance, η_Cη_A. The X_T ∼ η_Cη_A correspondence is clearly seen in Fig. 5B. The interplay between processivity and jamming of TrCel7A in affecting the apparent rate of cellulose decomposition also depends on the degree of polymerization of glucan chains and the boundary condition at the microfibril edge. These details are discussed in the supplemental data.

Unified Mechanistic Framework of Cellulose Decomposition via the Productivity Map

Because the surface inactivity of TrCel7A is predominantly due to slow complexation and excessive blocking, enhancement of cellulose decomposition likely requires simultaneous consideration of these two factors. SLATE simulations can be used to answer the following questions. If k_c and k_dc could be varied independently via protein engineering or substrate pretreatment while keeping the other rate constants unchanged, to what extent can the cellulose decomposition rate be increased? How do the optimal k_c and k_dc differ from those of native TrCel7A?

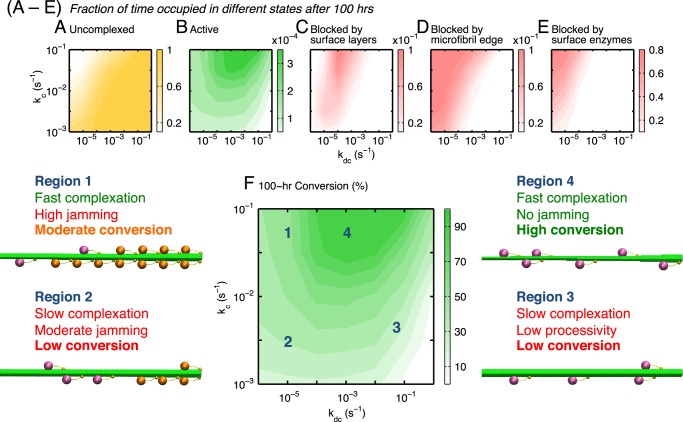
Fig. 6 (A–E) plots the fractional occupancy times in different enzyme states for 100 h of conversion by varying both k_c and k_dc. The competition between increasing the complexation driving force and reducing the fractions of blocked enzymes in maximizing the final conversion (productivity) is shown. The region of elevated occupancy in the active state in Fig. 6B can be reached via high complexation and intermediate decomplexation rates. In this scenario, the enzymes complex relatively quickly and process entire glucan chains on cellulose per complexation event without causing traffic jams. In this high activity region, the enzymes have a moderate occupancy fraction in the edge-blocked state but a minimal fraction in the enzyme-blocked state. Due to the X_T ∼ η_Cη_A correspondence discussed above, the contour of the enzyme fraction in the active state in Fig. 6B follows that of the 100-h conversion shown in Fig. 6F.

FIGURE 6.

Maps of fractional occupancy times (A–E) and productivity of conversion (F) in the complexation-decomplexation (k_c − k_dc) plane. The fractional occupancy time for a state is its occupancy time divided by the total reaction time. Four kinetics regions are identified in the productivity map of F, and a representative snapshot from a SLATE simulation is shown for each region. Enzymes in the blocked state are colored orange. The kinetic characteristics of each region are also described.

The productivity map in Fig. 6F not only reveals the rich behaviors of cellulase enzymes on the cellulose surfaces but can also be used to unify a diverse range of experimental observations. In Region 1 of Fig. 6F, conversion is limited by excessive jamming rather than slow complexation (30–32). This situation is analogous to experiments with amorphous cellulose, on which complexation occurs more quickly than on a crystalline substrate but enzyme jamming would be more prevalent (30–32, 45). In Region 2, both slow complexation and jamming are rate-limiting as seen in the decomposition of crystalline cellulose (12, 34). In Region 3, conversion is limited by complexation and low processivity, as in experiments with mutated cellulases on crystalline cellulose (45). To arrive at the high productivity of Region 4, enhancement of the complexation driving force must be simultaneously balanced with the competing requirement of having low jamming.

Because biomass feedstocks inevitably contain defects and obstacles originating from the high contents of hemicellulose and lignin (2, 11), the kinetic behaviors of TrCel7A enzymes on lignocellulosic substrates likely fall within Region 2 of Fig. 6F. A high density of surface obstacles is mechanistically analogous to a lower decomplexation rate constant in the SLATE model. In this regime, enhancing complexation and removing surface obstacles both need to be considered for increasing the apparent productivity. In addition to protein engineering, these objectives highlight the importance of pretreatment strategies for decrystallizing cellulose and/or removing surface obstacles (46).

Therefore, resolving the shift of enzymatic behaviors on the productivity map would be an informative way to assess the success of biomass pretreatment as well as cellulase engineering. In this regard, the occupancy time distributions of individual enzymes may be quantified in different scenarios via spatially resolved modeling of enzyme kinetics. Using the productivity map to reveal the effects of molecular configuration on enzyme kinetics can provide a general framework for uncovering the specific rate-limiting mechanisms of cellulose decomposition.

DISCUSSION

Kinetic simulations with the SLATE model at a molecular resolution elucidate the significant impact of interfacial confinement on cellulose decomposition by TrCel7A. The rate-limiting mechanisms were identified to be slow complexation of glucan chains and excessive enzyme jamming. Although complexation restrains the apparent rate of substrate conversion throughout the entire process, enzyme jamming develops with time and becomes more important and even dominant in slowing down the apparent rate as the reaction proceeds. The possibility of decomplexation-limiting kinetics on the substrate surface was inferred from bulk experiments (30–32), and spatially resolved simulations delineate the quantitative bounds and molecular origins of its occurrence. The ability to track individual enzymes and the structural evolution of the substrate at the same time also unifies the diverse kinetic behaviors of cellulose decomposition observed in different experiments. An emergent message is that a one-cause, time-independent explanation of enzyme inefficiency provides an oversimplified and incomplete view. Single-faceted approaches are also likely to be insufficient for understanding other processes of interfacial biocatalysis.

The passing flows of processive cellulases along microfibrils (12) as well as motor proteins along filaments (14) resemble in many respects vehicular travel along a highway. The reducing ends of glucan chains are analogous to the narrow ramps restricting the entrance of processing enzymes onto the microfibril. The nonreducing edge of the microfibril acts as a “roadblock” that stops the flow of forward-moving enzymes and causes traffic jams. These conditions can be avoided by introducing exit ramps via decomplexation. However, too high a rate constant of decomplexation for the enzyme would lead to excessive detouring off the highway traffic and reduction of the processive enzyme flows that decomposes the substrate. Therefore, a balanced optimization of the complexation-exchange kinetics of TrCel7A is required to enhance the travel conditions of enzymes along microfibrils and hence accelerate the overall rate of cellulose decomposition.

The presence of structural heterogeneity in interfacial biocatalysis demands a spatially resolved approach to describe enzyme kinetics. For the case of enzymatic cellulose decomposition, the SLATE model illustrates that accounting for molecular scale resolution under surface restriction is indispensable for uncovering the kinetic bottlenecks. Because heterogeneous and crowded environments are ubiquitous in biological systems, the development of SLATE represents an important step toward a systems-level analysis of the spatiotemporal behaviors of enzyme reaction networks.