Abstract
Computational fluid dynamic (CFD) simulation is a powerful tool in the design and implementation of microfluidic systems, especially for systems that involve hydrodynamic behavior of objects such as functionalized microspheres, biological cells, or biopolymers in complex structures. In this work, we investigate hydrodynamic trapping of microspheres in a novel microfluidic particle-trap array device by finite element simulations. The accuracy of the time-dependent simulation of a microsphere's motion towards the traps is validated by our experimental results. Based on the simulation, we study the fluid velocity field, pressure field, and force and stress on the microsphere in the device. We further explore the trap array's geometric parameters and critical fluid velocity, which affect the microsphere's hydrodynamic trapping. The information is valuable for designing microfluidic devices and guiding experimental operation. Besides, we provide guidelines on the simulation set-up and release an openly available implementation of our simulation in one of the popular FEM softwares, COMSOL Multiphysics. Researchers may tailor the model to simulate similar microfluidic systems that may accommodate a variety of structured particles. Therefore, the simulation will be of particular interest to biomedical research involving cell or bead transport and migration, blood flow within microvessels, and drug delivery.
INTRODUCTION
In recent years, microfluidic systems have received great interest in life science, biochemistry, pharmacology, and medical diagnostics.1, 2, 3 By miniaturizing and integrating diverse functionalities, microfluidic systems provide the ability to perform laboratory operations on small scales (i.e., lab-on-a-chip devices). They can synthesize and analyze small volumes of sample, minimize reagent consumption, integrate high-throughput sample processing steps, and reduce processing time, all of which provide great promise for both fundamental research and practical applications. Most microfluidic systems involve complex mixtures of biological particles, such as functionalized microspheres or colloids4, 5 and cell suspensions.6 Applications of these microfluidic systems include biomolecule detection and profiling,7, 8 microsphere-based micromixing and immunoassays,9, 10 and cell sorting and separation.11, 12 For example, the experiments of sorting, separation, and trapping of CTCs have been performed using microfluidic systems with similar hydrodynamically engineered configurations.13, 14, 15 To optimize the functionalities of these systems, one needs to understand the hydrodynamic behavior of the particles so as to manipulate them in a controlled manner. Karimi et al. briefly reviewed the hydrodynamic mechanisms of cell and particle trapping.16 However, microfluidic devices are not simply scaled-down versions of the conventional macro-scale systems. Because the dimensions of a microfluidic structure are small, particles suspended in a fluid become comparable in size to the structure itself, which dramatically alters the system's behaviors. As a result, the fluidic dynamics are rather complicated and are affected by many parameters, i.e., the fluid viscosity, velocity, and pressure, the device geometry, the particle number, shape, and elastic flexibility (specially for blood cells or emulsions), and the fluid-particle interactions. The interactive complexity of these parameters often prevents a holistic understanding of the systems, making it difficult to achieve reliable designs and effective experimental operation.
To study the microfluidic systems, computational fluid dynamic (CFD) simulations coupled with solid mechanics have become an increasingly important tool. By incorporating the complexities of its parameters, the microfluidic system's hydrodynamic behavior can be predicted and visualized, even though the system's minute dimensions make them difficult to prove via explicit mathematical methods or experiments. Therefore, the simulations help researchers assess design alternatives at reduced cost and guide experimental operation.17, 18 For a particle-based target detection platform19 as an example, microspheres with receptors on their surfaces to capture biological targets (DNAs, RNAs, or proteins) are immobilized by the trap arrays through microfluidic techniques. The trap array geometry must be rationally designed to maximize the trapping efficiency of microspheres and minimize fluidic errors (i.e., traps that are occupied by no or multiple microspheres, or traps with clogged channels). The importance of hydrodynamic property in the successful trapping of the microspheres, demonstrated in our previous publication,19 highlighted the value of CFD simulations in predicting and investigating the movement of microspheres in the microfluidic device.
To address this need, in this work, we create a finite element (FEM)20 simulation model to study the hydrodynamic trapping of microspheres in our microfluidic particle-trap array device.19 To our knowledge, no similar systems have been simulated before. Therefore, our simulation will be a significant addition to the existing toolbox on the theoretical design and understanding of increasingly complex hydrodynamically engineered microfluidic systems. A time-dependent simulation of a microsphere's trapping process shows excellent agreement with the experimental observation, which benchmarks the microfluidic device. Based on the simulation, we investigate the fluid velocity field, pressure field, and force and stress on the microsphere in the device. We further explore the trap's geometric parameters and the critical fluid velocity, above which subsequent microspheres would not bypass the already-filled trap but would collide with it. Selecting appropriate geometric parameters and obtaining the critical fluid velocity are helpful to ensure efficient trapping of microspheres and reduce potential fluidic errors in the device.
While we employ the FEM simulation to study the hydrodynamic trapping of microspheres in the microfluidic particle-trap array systems, one can tailor and customize it for similar microfluidic systems with complex structures and may involve different particles. We implement the simulation in COMSOL Multiphysics21 and release it on our website by following the link in Ref. 22. The simulation set-up discussed in this paper can also provide some guidelines to help future users to tailor the model to their specific problems.
This paper is organized as follows. In Sec. 2, we outline the theoretical fundamentals of the numerical model. In Sec. 3, we present the configuration of the microfluidic particle-trap array device. Then, we discuss the simulation set-up in detail. In Sec. 4, we compare the simulated trapping process for one microsphere with our experimental results, in terms of the microsphere's displacement over time. For the fluid, we present its velocity and pressure fields. For the microsphere, we compute its velocity and the total force acting on it. We also show the stress on and deformation of the microsphere. We further explore the trap's geometric parameters and fluid velocities, which affect the microsphere's motion towards the trap. At the end of this section, the merits and limitations of the model are discussed. Section 5 concludes the paper.
THEORETICAL FUNDAMENTALS
The conceptual principles of the simulation model for the microfluidic system are straightforward. In this system, the fluid flow is described by the Navier-Stokes equations,23 and the particles (e.g., microspheres) obey linear elastodynamics and Newton's equation of motion.24 The coupling of fluid flow and solid mechanics is implemented by fluid-solid interaction, where the fluid imposes force on the particles' surfaces from fluid pressure and viscous drag. The finite element method (FEM)20 is employed to create a mesh of the simulation domain and discretize governing equations for solutions. Due to the movements and interactions of the fluid and particles, the mesh geometry is continuously moving and deformed. The arbitrary Lagrangian-Eulerian (ALE) technique25 is further employed to describe the dynamics of the deforming geometry and moving boundaries of the mesh, which helps create a new mesh and maintains numerical stability and accuracy. Table TABLE I. summarizes required and changeable input parameters and output variables in the simulation model. Detailed equations are presented next.
TABLE I.
Input parameters and output variables for the simulation model.
| Input parameters |
|---|
| Geometry of the microfluidic device (e.g., device length L (m), width W (m), height H (m)) |
| Location and geometry of obstacles in the device, if any |
| Location, release method, and shape of the particles (e.g., spherical particle radius r (m)) |
| Properties of the fluid (e.g., fluid density (kg/m3), dynamic viscosity (Pa·s), volume force affecting the fluid (N/m3)) |
| Properties of the particles (e.g., particle density (kg/m3), Young's Modulus (Pa), Poisson ratio ) |
| Inlet and outlet conditions (e.g., velocity (m/s), pressure (Pa), stress (N/m2), or mass flow (kg/s)) |
| Boundary conditions of device sidewalls and obstacles (e.g., no-slip wall) |
| Initial conditions of the fluid and the particles |
| Properties of mesh (scale and size ) |
| Computation set-up (e.g., time range (s), time step size (s), relative tolerance, solver type, etc.) |
| Basic output variables, from which other variables of interest can be computed |
|---|
| Fluid velocity field (m/s, m/s, m/s) |
| Fluid pressure (Pa) |
| Particle displacement field (m, m, m) |
| Particle infinitesimal strain tensor |
| Particle Cauchy stress tensor |
| Volume force affecting the particle (N/m3) |
| Coordinates of the spatial frame x,y,z |
| Coordinates of the material frame X,Y,Z |
Fluid flow
The fluid flow in microfluidic systems, if assumed incompressible, is described by the Navier-Stokes equations,23
| (1) |
| (2) |
where denotes the fluid density (kg/m3), the fluid velocity field (m/s, m/s, m/s), t the time (s), the pressure (Pa), the divergence operator, the gradient operator, I the identity matrix, and the fluid dynamic viscosity (Pa·s). Moreover, represents the unsteady inertia force (N/m3), represents the non-linear inertia force, and is the volume force affecting the fluid (N/m3, or N/m2 for a 2D model). For a pressure-driven flow without gravitation or other volume forces, . Given the values of , t, , and , the Navier-Stokes equations solve for and .
Due to the high computational demand in three dimensional (3D) fluidic dynamics simulation, two dimensional (2D) simulation is preferred. For microfluidic channels with an almost rectangular cross section where the thickness is much less than the channels' width, simple 2D models often fail to give correct results because they exclude the boundaries, which have a great effect on the flow. To consider the effect of these boundaries, shallow channel approximation is proposed.23 The approximation adds a drag term as a volume force to the fluid flow equation, which represents the resistance that the parallel boundaries place on the flow. The form of the drag term is
| (3) |
where H is the channel thickness (m).
Because of the microfluidic system's small dimensions and fluid velocities, the Reynolds number (l is the characteristic length and U is the average velocity) of the flow is small (). Thus, the flow stays laminar over most of the area.23 When the velocities of the fluid are very small, becomes very low (). The Strouhal number (F is the frequency of vortex shedding) is large (order of 1), and viscosity dominates the fluid flow, resulting in a collective oscillating movement of the fluid. Under this circumstance, flow in the system becomes Stokes flow (also called creeping flow), and the unsteady inertia force greatly dominates over the non-linear inertial force. Therefore, the non-linear inertial force can be neglected. Combining the shallow channel and Stokes flow approximations with the incompressible Navier-Stokes equations, Eq. 1 becomes
| (4) |
Solid mechanics
The solid, if assumed to undergo small deformation and subjected to low load, has isotropic linear elasticity. The displacement and deformation of the solid satisfy the governing equations of linear elastodynamics,24
| (5) |
| (6) |
| (7) |
Here, Eq. 5 is the strain-displacement (compatibility) equation, with denoting the infinitesimal strain tensor and denoting the solid displacement field (m, m, m). Equation 6 is Newton's equation of motion, with the Cauchy stress tensor, the body force per unit volume (N/m3) or boundary force per unit area in 2D (N/m2), and denoting the solid density (kg/m3). Equation 7 is the linear elastic stress-strain law, with C as the stiffness matrix given by
| (8) |
where is Young's modulus of the solid (Pa), and is the Poisson ratio of the solid.
Given the values of , t, , , and , Eqs. 5, 6, 7, 8 solve for , , and .
Fluid-solid interaction (FSI)
The FSI couples fluid flow with solid mechanics to capture the interaction between the fluid and the solid, which is applied through their boundary. It defines the fluid load on the solid and how the solid displacement affects the fluid's velocity,
| (9) |
| (10) |
where Eq. 9 presents the total force (caused by the fluid pressure and viscous force) exerted on the solid boundary, and n is the outward normal to the boundary. From Eq. 10, on the fluid-solid boundary the fluid velocity equals the rate of change for the displacement of the solid . In other words, the solid boundary acts as a no-slip wall for the fluid domain.
FEM20 is employed to create a mesh of the simulation domain and discretize the governing Eqs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, so as to approximate the solutions within a mesh element using simple functions. For a time-dependent problem, the Navier-Stokes equations of the fluid flow are solved using an Eulerian description and a spatial frame. Explicitly, the mesh in the fluid domain is freely moving, with initial mesh displacement as zero. With each moving mesh element, a smoothing function is associated and leads to effective forces between neighboring elements, resulting in substantial redistribution and deformation of the whole configuration of the mesh. The solid mechanics are formulated using a Lagrangian description and a material (reference) frame. That is, the mesh in the solid domain is fixed and undeformed.25 Therefore, the force on the solid is a transformation of ,
| (11) |
where and are the mesh element scale factors for the spatial frame and the material frame, respectively.
To combine the interface between the spatial frame of the fluid and the material frame of the solid, the arbitrary Lagrangian-Eulerian (ALE) method is employed,25 which computes new mesh coordinates based on both the movement of the solid's boundary and mesh smoothing of the fluid.
Boundary and initial conditions
The fluid flows from the channel inlet to the outlet, driven by the pressure difference between the inlet and the outlet. At the inlet, the flow is defined to have fully developed laminar characteristics with a parabolic velocity profile and mean velocity (m/s). By defining a parabolic velocity profile instead of a constant velocity, one ensures a better convergence of the nonlinear solver at the beginning. A simple definition of the inflow velocity profile for a rectangular channel is23
| (12) |
where W is the width of the inlet, and Y is the material frame coordinate along the inlet.
At the outlet, the boundary condition is defined as vanishing viscous stress along with a Dirichlet condition on the pressure:
| (13) |
On the solid walls, such as the simulation domain sidewalls and the fixed obstacles (e.g., traps in our particle-trap array device), no-slip wall condition is applied to the fluid,
| (14) |
and the prescribed mesh displacements of these walls are defined as zero.
For the initial values of the fluid velocity field , pressure , particle displacement field , and particle velocity field , one can assign specific values if there are good estimations. Otherwise, one can set them as zeros for simplicity.
FROM DESIGN TO SIMULATION
We apply the finite element simulation to our microfluidic particle-trap array device design and validation.19, 26 We also investigate the set-up requirements of the simulation, including the selection of mesh scales, moving mesh conditions, time step size, solver types, etc.
Configuration of the microfluidic particle-trap array device
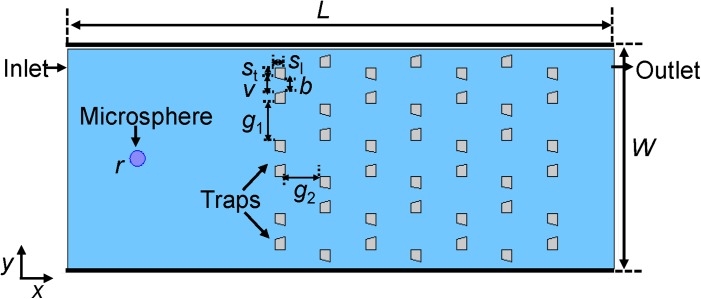
Figure 1 presents a schematic of the microfluidic particle-trap array device. The microfluidic channel has an inlet on the left side and an outlet on the right side. The traps in the channel are made of polydimethylsiloxane (PDMS), with each trap shaped as inverted-trapezoid grooves. The trap arrays are periodic, with each row offset horizontally with respect to the one ahead of it. A liquid solution (water) carrying polystyrene microspheres of radius r = 5 μm flows from the inlet and through the channel. We note that the microspheres are the only “solid” to be considered in the equations of the solid mechanics and the fluid-solid interaction described in Sec. 2, while the traps are assumed to be fixed and act as the no-slip boundary to the fluid. In simulations, one usually can shorten the length and the width of the channel with respect to the real device to reduce the computation, without changing its hydrodynamic characteristics. One also can make other appropriate simplifications of the experimental situation. As the inlet effectively injects single or several microspheres into the channel at a time, the inflow of microspheres can be emulated in the simulation by a generic source of microspheres placed at a certain distance away from the traps. The geometric parameters of the trap array device26 and the present simulation parameters are given in Table TABLE II..
Figure 1.
Schematic diagram of a microfluidic particle-trap array device. The microfluidic channel has an inlet on the left side and an outlet on the right side. The traps in the channel are made of polydimethylsiloxane (PDMS), with each trap shaped as inverted-trapezoid grooves. The trap arrays are periodic, with each row offset horizontally with respect to the one ahead of it. A liquid solution carrying a particle (e.g., polystyrene microsphere) of radius 5 μm flows from the inlet and through the channel. The values of the device's geometric parameters are given in Table TABLE II..
TABLE II.
Present simulation parameters a.
| L (channel length) | 360 μm | ||
| W(channel width) | 140 μm | ||
| H (channel height) | 20 μm | ||
| v (upper width of trap opening) | 10 μm | ||
| b (bottom width of trap opening) | 7.6 μm | ||
| (upper width of groove walls) | 6.6 μm | ||
| (length of groove walls) | 6.6 μm | ||
| h (height of groove walls) | 16.5 μm | ||
| (gap between two neighboring traps on the same row) | 23.3 μm | ||
| (gap between two successive row) | 23.3 μm | ||
| r | 5 μm | ||
| 1000 kg/m3 | |||
| 0.001 Pa·s | |||
| 70 μm/s | |||
| 1050 kg/m3 | |||
| 3 MPa | |||
| 0.33 | |||
| 0.001 s |
Mesh scale is provided in Table TABLE III..
Assessment of the simulation
The flow through the device (Figure 1) is characterized by the Reynolds number (). In our case, the characteristic length l is the microsphere's diameter , and U is the relative velocity between the steady state flow and the microsphere. Therefore, when the relative velocity ≪10 cm/s and , the system can be treated at the asymptotic limit of Stokes flow.23
As for the thermal motion (Brownian motion), its relative importance can be characterized by the Peclet number ,27
| (15) |
where (m/s) is the velocity of the microsphere, L (m) is a typical distance that the microsphere can travel (say, the distance from the inlet to outlet of the microfluidic channel), is the Einstein expression for the diffusion coefficient of a spherical particle of radius r (m/s), is the Boltzmann constant, and T (K) is the experiment temperature. In our case, is much larger than 1. Thus, the thermal motion of the microsphere is negligible27 and is not considered in our simulation.
Mesh creation, smoothing, independence test, and remeshing
As we mentioned in Sec. 2, to solve the governing equations, FEM is employed to create a mesh of the simulation domain and to discretize the equations. The ALE technique is used to describe the interface between the fluid and the microsphere. During the time-dependent solution process, the mesh in the microsphere domain is fixed and undeformed, while the mesh in the fluid domain is freely moving and deformed in response to mesh smoothing and the movement of the microsphere. For the mesh smoothing function, Winslow smoothing or hyperelastic smoothing is recommended.28, 29 Both smoothing methods are nonlinear and robust, and work well for our problem. The hyperelastic method can give a smoother result than Winslow does, particularly in regions where the mesh is highly stretched. Therefore, when the solid particle has large elasticity (e.g., a blood cell) with large deformation expected, the hyperelastic method is more suitable.
Figure 2 presents the initial mesh (with free triangular shape) at t = 0 s, which is generated prior to solving the model. Though the mesh is not uniform, with denser and smaller elements at the fluid-solid boundaries and looser and larger elements in the fluid domain, the mesh is equally distributed around the microsphere. Figure 2 also illustrates how the mesh moves with a continuously deforming geometry at a series of subsequent time points t = 0.275 s, 0.641 s, 0.916 s, and 1.191 s. Because the microsphere is moving along the x direction, the mesh is also moving in this direction (shown by the red arrows in the figure).
Figure 2.
Mesh and geometry movement and deformation at a series of time points: initial mesh (full-size plot) at t = 0 s, and deformed mesh (zoomed-in plots) at t = 0.275 s, 0.641 s, 0.916 s, and 1.191 s. The microsphere, which is underneath the densest meshes in each plot, is shown in red. The arrows represent the mesh direction and velocity, with their sizes indicating the velocity magnitude.
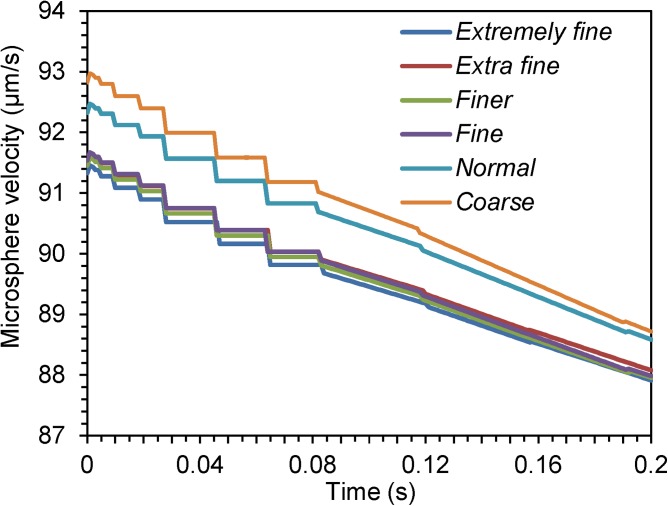
As exact analytical solutions to the equations are unknown, a mesh independence test can be used to choose an appropriate mesh size. It is performed by increasing the mesh size (denoted as mesh scale) until the difference between the results for two successive mesh scales is negligible. Table TABLE III. presents the properties of different mesh scales, and the degrees of freedom in solving the equations. Figure 3 plots the velocity of the microsphere at t = 0 s ∼ 0.2 s under different mesh scales. It can be seen that the differences among the velocities for the mesh scales fine, finer, extra fine, and extremely fine (as defined in Table TABLE III.) are very small. Considering the computational efficiency and to reduce the chance that the solver might not converge at an extreme, the scale finer is used for subsequent simulation.
TABLE III.
Mesh scales in mesh independence study.
| Mesh scale | Maximum element size (μm) | Minimum element size (μm) | Maximum element growth rate | Resolution of curvature | Number of elements | Degrees of freedom |
|---|---|---|---|---|---|---|
| Extremely fine | 0.938 | 0.028 | 1.05 | 0.25 | 167 324 | 408 559 |
| Extra fine | 1.82 | 0.21 | 1.08 | 0.25 | 46 780 | 114 918 |
| Finer | 3.92 | 0.56 | 1.1 | 0.25 | 12 214 | 30 759 |
| Fine | 4.9 | 1.4 | 1.13 | 0.3 | 9708 | 24 299 |
| Normal | 6.3 | 2.8 | 1.15 | 0.3 | 7629 | 18 794 |
| Coarse | 9.28 | 4.2 | 1.2 | 0.4 | 2942 | 7518 |
Figure 3.
Time-dependent plots of the microsphere's velocity along the x direction at different mesh scales.
When the mesh deformation of ALE becomes large (in our case when the microsphere draws near to the trap), the quality of the mesh created by the smoothing function deteriorates and the mesh elements may be (partially) warped inside-out (inverted coordinates). Inverted coordinates do not mean a failure of the simulation, but they do imply that results at these elements will not be used in further iterations. If these elements are not in the vicinity of the area of interest, the simulation is still expected to be reliable. However, if there are many inverted coordinates, the accuracy of the solution is reduced and the solver runs into convergence problems. To solve this issue, a new mesh can be generated for the region covered by the deformed mesh, and then letting the solver continue by deforming the new mesh. Explicitly, we define a requested mesh quality (as a scalar number between 0 and 1, typically smaller than 0.2). When the mesh quality becomes smaller than the requested one, the solver stops and remeshes at a previously stored solution time. Then the simulation continues using the new mesh from this solution time.
Selection of time step size
The time step size (s) affects the numerical stability, accuracy, and efficiency of the computation. The selection of can be quite complex and here we provide only some guidelines. First of all, an appropriate should satisfy the necessary Courant-Friedrichs-Lewy (CFL) condition (), where U (m/s) is the velocity and (m) is the mesh size.30, 31 Then, one can use a single for the simulation time. However, this may result in a too small and an inefficient computation. Alternatively, one can use a that meets the local CFL condition. In such an arrangement, most of the computation is concentrated in simulation time ranges with the finest mesh and largest mesh deformation. In the time ranges of coarse mesh and small mesh deformation, the solution is updated only occasionally with a much larger .
Selection of solvers
To solve the time-dependent simulation problem, we consider two solution approaches, fully coupled or segregated. For the fully coupled solver, the multiple physics from Eqs. 1 to 14 are coupled together. Thus, the fluid velocity and pressure, as well as the microsphere motion, stress, and strain are solved at the same time. For the segregated solver, the solution process is split into several steps. Explicitly, for a current microsphere position, the fluid flow is solved using the velocities at the microsphere surface from the previous step, which used the fluid-solid interaction boundary condition Eq. 10 and fluid flow Eqs. 1, 2, 3, 4. Then the total force, which includes viscous and pressure terms from the fluid, is evaluated at the microsphere surface (Eqs. 9, 11). The force is further used in Eqs. 5, 6, 7, 8 for defining the microsphere's motion and deformation. In our case, we observe that the segregated solver takes a lot more computational time than the fully coupled solver does, and its estimated error of solution (on the order of 106) is also much larger than that of the fully coupled one (on the order of 10). Therefore, the fully coupled solver is employed. Moreover, we choose a damped version of Newton's method for the solver, and let the solver automatically determine the damping factor in each iteration.32
SIMULATION RESULTS, VALIDATION, AND DISCUSSION
In this section, we present the simulation results of the hydrodynamic trapping in the microfluidic particle-trap array device. First, to validate the accuracy of the simulation, we performed a microsphere trapping experiment using the device and compared the experimental results with the simulation in terms of the microsphere's displacement over time. Then, we investigate the simulation results of some variables that are difficult to measure experimentally in the trapping process. For the fluid, we provide its velocity and pressure fields. For the microsphere, we compute its velocity and the total force on it. We also show the stress on and deformation of the microsphere. We further explore the trap's geometric parameters and the critical fluid velocity, above which the subsequent microspheres would collide with, instead of bypassing, a trap that is already filled by a microsphere. Finally, the merits and limitations of the model are discussed.
Flow velocity field and microsphere displacement: Simulation versus experiment
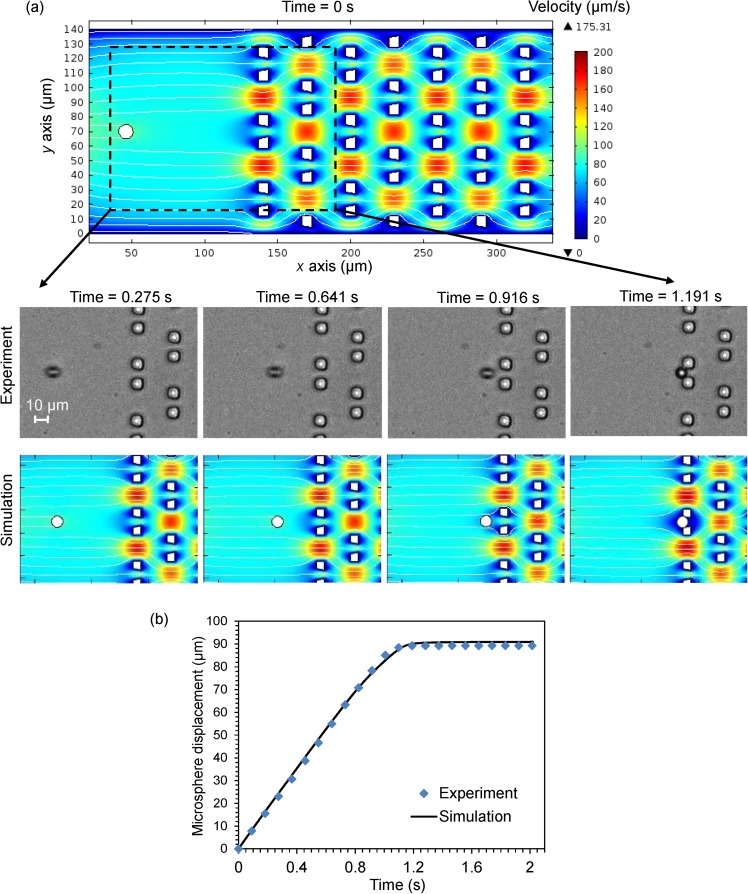
Figure 4a presents the simulated flow velocity field at a series of time points (full size plot at t = 0 s, and zoomed-in plots at t = 0.275 s, 0.641 s, 0.916 s, and 1.191 s). The streamlines indicate the flow direction, and the rainbow color represents the flow-velocity magnitude distribution with a fixed value range for all plots. We observe that the flow moves faster through the gaps among the traps, and smaller through the traps due to the traps' small openings. The flow's velocity is zero at the boundaries of the traps. The streamlines clearly show that there are no vortices in the creeping flow. Moreover, only the flow in close proximity to the microsphere is affected by the microsphere's motion. Once a trap is filled by the microsphere, the flow is blocked at the trap.
Figure 4.
(a) Flow velocity field at a series of time points (full size plot at t = 0 s, and zoomed-in plots at t = 0.275 s, 0.641 s, 0.916 s, and 1.191 s). The streamlines indicate the flow direction, and the rainbow color represents the flow-velocity magnitude distribution with a fixed value range for all plots. These plots also present the positions of a 10μm microsphere at these different time points in the experiment and in the simulation. (b) Time-dependent plots of the displacements of the microsphere along the x direction in the simulation and in the experiment. Video recordings, one of the experiment and one of the simulation of the whole process (t = 0 s ∼ 2.02 s) are in Video S1 and Video S2,33 respectively.
Figure 4a also shows the positions of a microsphere at the different time points in the experiment and the simulation. Figure 4b further compares the time-dependent displacements of the microsphere along the x direction in the experiment and in the simulation. The displacement of the microsphere increases almost linearly and finally stays constant when the microsphere gets immobilized at the trap. The simulation results agree well with the experiment. Two videos recordings of the experiment and of the simulation of the microsphere's trapping process (t = 0 s ∼ 2.02 s) are provided in Video S1 and Video S2 in the supplementary material.33
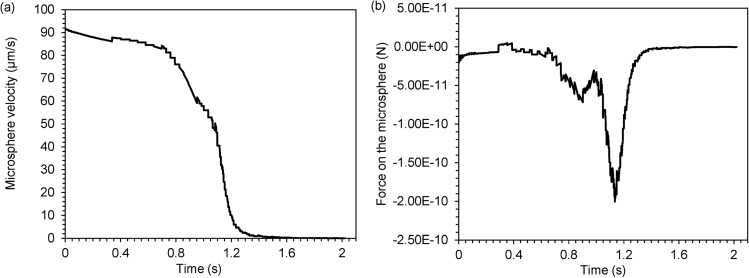
Microsphere velocity and total experienced force
Figure 5 presents time-dependent plots of the microsphere's velocity (5(a)) and experienced total force (5(b)) along the x direction. At the beginning, when the microsphere is far away from the trap, it has almost the same velocity as that of the surrounding steady-state fluid, and thus experiences little force from the fluid. As the microsphere flows toward the trap, the velocity of the fluid ahead decreases because of the trap in path, and exerts negative drag on the microsphere. When the microsphere is very close to the trap, it experiences a large negative force and its velocity reduces sharply. Finally, the total force (force imposed by the trap and fluid force) and velocity become zero when the microsphere is immobilized at the trap.
Figure 5.
Time-dependent plots of the microsphere's (a) velocity and (b) experienced total force, along the x direction.
We note that the line plots of the velocity and force are not smooth and have discontinuities. Because the velocity is the displacement's first derivative and the force is related to its second derivative, when the sizes of the discrete elements in solving the equations are not infinitely small, any small perturbation in the solution of displacement will result in large discontinuities in its derivatives. There is even a peak in the force plot before this variable decreases sharply. Remeshing and solution mapping seem to have resulted in the peak, because at that time the gap between the microsphere and the trap is too small to cause severe mesh deformation.
Flow pressure field
Figure 6 shows the pressure field of the flow at a series of time points (full size plot at t = 0 s, and zoomed-in plots at t = 0.275 s, 0.641 s, 0.916 s, and 1.191 s). The rainbow-colored contour represents the pressure magnitude distribution: the magnitude of the pressure at the inlet is the greatest and it gradually decreases along the channel until the outlet. However, we note that the pressure at the outlet is actually predefined as zero through boundary condition Eq. 12, which may not be the real situation. An accurate description of pressure boundary conditions merits application-specific refinements.
Figure 6.
Flow pressure field at a series of time points (full size plot at t = 0 s, and zoomed-in plots at t = 0.275 s, 0.641 s, 0.916 s, and 1.191 s). The rainbow-colored contour represents the pressure magnitude distribution. The pressure magnitude ranges of the plots are the same (0 Pa ∼ 1.711 Pa) except for that of the plot at t = 1.191 s (0 Pa ∼ 3.3239 Pa), where the greatest pressure (3.3239 Pa) occurs in the very small gap between the microsphere and the trap.
When the microsphere is far from the trap, it is impacted only by the flow pressure and viscous drag surrounding it. When the microsphere is close to the trap, the pressure between the microsphere and the trap increases and imposes negative force on the microsphere. When the microsphere is immobilized at the trap, the pressure in the very small gap between the microsphere and the trap becomes even larger than that at the inlet. Therefore, to ensure the stable trapping of the microsphere, i.e., the microsphere is retained in the trap and is not swept away due to the transient flow motion around the trap, a persistent pressure should be provided at the inlet.
Stress on the microsphere
Figure 7 presents the von Mises stress on the microsphere at a series of time points (zoomed-in plots at t = 0 s, 0.275 s, 0.641 s, 0.916 s, and 1.191 s). The von Mises stress34 is a scalar stress value computed from the stress tensor of a solid, which is often used in determining whether a particle will yield when subjected to a complex loading force. In this figure, the traffic color on the microsphere represents the stress magnitude distribution. The maximum and minimum stress points are also presented. When the microsphere is far from the trap, the stress on the microsphere is almost a constant and is uniformly distributed, although due to the larger fluid pressure the stress close to the inlet is a bit larger than that of the outlet. When the microsphere is trapped, because of the force from the trap, the stress on the microsphere increases dramatically, especially at the contact points of the microsphere. Nevertheless, the stress is not sufficient to cause any obvious deformation of the microsphere, due to its low elasticity.
Figure 7.
Stress on the microsphere at a series of time points (zoomed-in plots at t = 0 s, 0.275 s, 0.641 s, 0.916 s, and 1.191 s). The color of the microsphere represents the stress magnitude distribution, and the maximum and minimum stress points on the microsphere are also presented in blue color.
If the trap array device is applied to trap biological cells (e.g., blood cells), the investigation of stress acting on the cells is useful. Stress can lead to biological and biochemical consequences in cells, such as cell deformation, differentiation, and even cell death.35, 36 Simulation will help select proper experimental conditions (fluid pressure, velocity, trap material, etc.) that avoid undesired damage of the fragile particles.
Investigations of trap's geometric parameters and critical fluid velocity
The microfluidic particle-trap array device employs fluidic resistance and path engineering to perform precise hydrodynamic trapping of micron-scaled particles.19 During the loading process, a particle (a microsphere in our case) in the fluid has two possible flow paths, trapping or bypassing. Here, trapping is defined as a microsphere flowing into the trap, and bypassing is defined as the flow of subsequent microspheres through the channels next to the trap. This scheme for a single trap is applicable for all the traps. The trap array geometry should be designed so that the trapping path for an empty trap has a lower flow resistance than the bypassing path. Then the microsphere is most likely to move into an empty trap through trapping. However, once the trap through trapping is loaded by a microsphere, the flow resistance in trapping dramatically increases and is much larger than that in bypassing, and thus subsequent microspheres divert to the bypassing path and get immobilized by another trap downstream.
Now, we employ the simulations to explore the critical fluid velocity and the critical trap width, above which the subsequent microspheres would collide with the filled trap by its inertia, instead of bypassing the trap. Such collision prevents us from operating the microspheres' trapping process in a controlled manner and may cause large fluidic errors. The critical velocity found in the simulations suggests that microsphere-trapping experiments be operated below this velocity. The critical trap width found in the simulations adds an additional optimization constraint (i.e., upper limit of the trap width) to the optimal design framework of the device in our previous work.19
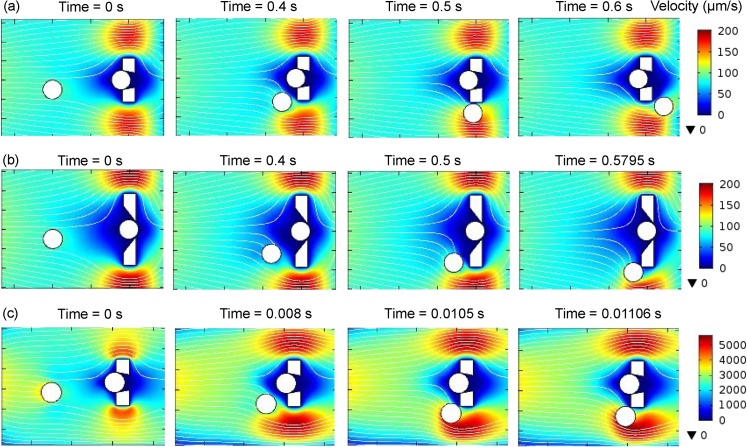
To study the effect of the trap width, both v (upper width of trap opening) and (upper width of groove walls) can be adjusted. Here, we gradually increase v from 10 μm and keep μm constant. For a feasible fabrication, the value of is selected to ensure that the aspect ratio (the ratio of transverse dimensions to height μm) is greater than 0.4.26 The other geometric parameters of the trap array are also kept constant as given in Table TABLE II.. To eliminate simulation symmetry, the microsphere is released 5 μm off the centerline of y direction of the flow domain. Figure 8a shows that at μm and an inlet mean velocity μm/s, the microsphere easily bypasses the trap. When the width of the trap increases, the zero-flow-velocity area increases and the microsphere has to travel a longer distance along the trap to bypass it. Our simulation indicates that when v increases to 24 μm (Figure 8b), the microsphere collides with the trap. Therefore, to ensure efficient bypassing of the occupied trap, v should not be larger than 24 μm. On the other hand, v should not be too small compared with the microsphere's diameter. Otherwise, the microsphere gets only its bottom clamped in the trap and is easily swept away by the transient flow around it.
Figure 8.
Effects of trap width and fluid velocity on the microsphere's motion toward a filled trap, shown by zoomed-in flow velocity field plots. The streamlines indicate the flow direction, and the rainbow color represents the flow-velocity magnitude distribution. (a) When the upper width of the trap opening v = 10 μm and the inlet mean velocity = 70 μm/s, the microsphere easily bypasses the filled trap. (b) When is fixed at 70 μm/s and increases to 24 μm, the microsphere collides with the boundary of the trap. (c) When is fixed at 10 μm and increases to 2500 μm/s, the microsphere also collides with the boundary of the trap.
To study the effect of fluid velocity, we keep the trap's geometric parameters constant and gradually increase the inlet mean velocity . As shown in Figure 8c, when increases to 2500 μm/s, the microsphere collides with the boundary of the trap. Therefore, we estimate 2500 μm/s as the critical fluid velocity, and would suggest that microsphere-trapping experiments be operated below this velocity.
Note that in this subsection's simulations, the mesh size is assigned to be extremely fine and the time step size is set as −6 s, to ensure the convergence of the solver and the accuracy of these critical parameters.
Discussion
Numerical simulation may not exactly replicate events in reality, especially when some physical phenomena are not considered or incorporated in the model. Numerical approximations in the finite element method also lead to slightly inaccurate simulation results. However, careful examination of simulation results and comparison with the experimental data can validate the use of the model as a benchmarking and explorative tool.
In this work, we focus on the hydrodynamic trapping of the microsphere, i.e., the interactions among fluid and the microsphere, the fluid viscous drag force and pressure exerted on the microsphere, and the microsphere's trajectories (displacements). The interactions among the microspheres, they are enabled by the changes of fluid flow. While the interactions actually comprise a variety of mechanisms and forces spanning several length scales, such as electrostatic, elastic, and other short range surface forces; these phenomena are difficult to represent at the present level of modeling. Nevertheless, in situations where the number of microspheres in the fluid is small, such as in our trap array device where the concentration of microspheres is carefully selected to avoid aggregation and channel clogging, the interactions among microspheres seldom happen. Therefore, for these situations, the overall numerical efficiency is not affected. Further refinements of the model could include the full hydrodynamic interactions between the microspheres.
Though we test only hydrodynamic trapping of microspheres in the particle-trap array systems in this paper, we have made the simulation customizable and openly accessible to other researchers and have provided guidelines on the simulation set-up, including how to choose the mesh properties, moving mesh conditions, time step size, and solver type. Therefore, one may tailor the simulation to investigate similar microfluidic systems with complex structures and may accommodate a variety of particles, such as colloids, biological cells (e.g., red blood cells, circulating tumor cells), polymers, and target-tagged microspheres, by modifying the properties of the particles (e.g., elasticity, structure). To our knowledge, such customizable and ready-to-use tools for similar microfluidic systems are not easily accessible for device fabricators or users. We believe this model will be of particular interests to biomedical research that may involve blood flow within microvessels, cell or particle transport and migration, bio-imaging, and drug delivery.
CONCLUSIONS
We have studied the hydrodynamic trapping in the microfluidic particle-trap array systems by finite element simulation. In the simulation, the time-dependent, laminar, and incompressible fluidic dynamics and solid mechanics equations are coupled and solved computationally through finite element techniques. The simulated hydrodynamics in the microfluidic channel impacting the moving microsphere agree well with the experimental observation. The study of the hydrodynamic trapping enables rational design on the geometric parameters, fluid velocity and pressure, and stress on the micro-particles in the flow. Therefore, the FEM simulations provide a powerful explorative tool in designing and implementing microfluidic devices.
ACKNOWLEDGMENTS
This work was supported by National Science Foundation (Grant No. CCF-0963742). The authors gratefully acknowledge the valuable discussions with Professor Ramesh Agarwal, Professor Qiulin Qu, and Dr. Zheming Zhang at the Mechanical Engineering & Materials Science Department, Washington University in St. Louis.
References
- Whitesides G. M., Nature 442(7101), 368 (2006). 10.1038/nature05058 [DOI] [PubMed] [Google Scholar]
- Janasek D., Franzke J., and Manz A., Nature 442(7101), 374 (2006). 10.1038/nature05059 [DOI] [PubMed] [Google Scholar]
- Yager P., Edwards T., Fu E., Helton K., Nelson K., Tam M. R., and Weigl B. H., Nature 442(7101), 412 (2006). 10.1038/nature05064 [DOI] [PubMed] [Google Scholar]
- Schwenk J. M. and Nilsson P., Methods Mol. Biol. 723, 29 (2011). 10.1007/978-1-61779-043-0_3 [DOI] [PubMed] [Google Scholar]
- Sugiura S., Oda T., Izumida Y., Aoyagi Y., Satake M., Ochiai A., Ohkohchi N., and Nakajima M., Biomaterials 26(16), 3327 (2005). 10.1016/j.biomaterials.2004.08.029 [DOI] [PubMed] [Google Scholar]
- Guo Q., Reiling S. J., Rohrbach P., and Ma H., Lab Chip 12(6), 1143 (2012). 10.1039/c2lc20857a [DOI] [PubMed] [Google Scholar]
- Xu X., Sarder P., Kotagiri N., Achilefu S., and Nehorai A., IEEE Trans. Nanobiosci. 12(1), 29 (2013). 10.1109/TNB.2012.2230116 [DOI] [PubMed] [Google Scholar]
- Choi J. W., Oh K. W., Thomas J. H., Heineman W. R., Halsall H. B., Nevin J. H., Helmicki A. J., Henderson H. T., and Ahn C. H., Lab Chip 2(1), 27 (2002). 10.1039/b107540n [DOI] [PubMed] [Google Scholar]
- Grumann M., Geipel A., Riegger L., Zengerle R., and Ducree J., Lab Chip 5(5), 560 (2005). 10.1039/b418253g [DOI] [PubMed] [Google Scholar]
- Roos P. and Skinner C. D., Analyst 128(6), 527 (2003). 10.1039/b300995e [DOI] [PubMed] [Google Scholar]
- Kulrattanarak T., Sman R. G. M., Schroën C. G. P. H., and Boom R. M., Microfluid. Nanofluid. 10(4), 843 (2011). 10.1007/s10404-010-0715-z [DOI] [Google Scholar]
- Dittrich P. S. and Schwille P., Anal. Chem. 75(21), 5767 (2003). 10.1021/ac034568c [DOI] [PubMed] [Google Scholar]
- Lv P. T., Tang Z. W., Liang X. J., Guo M. Z., and Han R. P. S., Biomicrofluidics 7(3), 034109 (2013). 10.1063/1.4808456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moon H. S., Kwon K., Hyun K. A., Sim T. S., Park J. C., Lee J. G., and Jung H. I., Biomicrofluidics 7(1), 014105 (2013). 10.1063/1.4788914 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cima I., Yee C. W., Iliescu F. S., Phyo W. M., Lim K. H., Iliescu C., and Tan M. H., Biomicrofluidics 7(1), 011810 (2013). 10.1063/1.4780062 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karimi A., Yazdi S., and Ardekani A. M., Biomicrofluidics 7(2), 021501 (2013). 10.1063/1.4799787 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erickson D., Microfluid. Nanofluid. 1(4), 301 (2005). 10.1007/s10404-005-0041-z [DOI] [Google Scholar]
- Roy P., Anand N. K., and Banerjee D., Microfluid. Nanofluid. 15(3), 397 (2013). 10.1007/s10404-013-1159-z [DOI] [Google Scholar]
- Xu X., Sarder P., Li Z., and Nehorai A., Biomicrofluidics 7, 014112 (2013). 10.1063/1.4793713 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepper D. D. W. and Heinrich J. C., The Finite Element Method: Basic Concepts and Applications (Hemisphere Publishing Corporation, Florence, 1992). [Google Scholar]
- See http://www.comsol.com/ for the descriptions of the software.
- See http://www.ese.wustl.edu/~nehorai/research/molec_imaging/COMSOL_simulation_model_of_a_microfluidic_system.mph to download the simulation model.
- Bruus H., Theoretical Microfluidics (OUP Oxford, New York, 2008). [Google Scholar]
- Bower A. F., Applied Mechanics of Solid (Taylor & Francis, Florence, 2011). [Google Scholar]
- Souli M. and Benson D. J., Arbitrary Lagrangian Eulerian and Fluid-Structure Interaction: Numerical Simulation (Wiley, Hoboken, 2013). [Google Scholar]
- Xu X., Li Z., kotagiri N., Sarder P., Achilefu S., and Nehorai A., in SPIE MOEMS-MEMS (International Society for Optics and Photonics, 2013), pp. 86151E. [Google Scholar]
- Patankar S. V., Numerical heat transfer and fluid flow (Hemisphere Pub. Corp., Bristol, 1980). [Google Scholar]
- Knupp P. M., presented at the Winslow Smoothing on Two-Dimensional Unstructured Meshes, Park City, UT, 1998.
- Triantafyllidis N. and Aifantis E. C., J. Elasticity 16(3), 225 (1986). 10.1007/BF00040814 [DOI] [Google Scholar]
- Oliveira E. R. D., Int. J. Numer. Methods Eng. 21(2), 229 (1985). 10.1002/nme.1620210204 [DOI] [Google Scholar]
- Tam C. K. W. and Kurbatskii K. A., Int. J. Comput. Fluid Dyn. 17(2), 119 (2003). 10.1080/1061856031000104860 [DOI] [Google Scholar]
- Shadid J. N., Tuminaro R. S., and Walker H. F., J. Comput. Phys. 137(1), 155 (1997). 10.1006/jcph.1997.5798 [DOI] [Google Scholar]
- See supplementary material at http://dx.doi.org/10.1063/1.4822030 for Videos S1 and S2.
- Leckie F. A. and Bello D. J. D., Strength and Stiffness of Engineering Systems (Springer; London, Limited, 2009). [Google Scholar]
- Eggleton C. D. and Popel A. S., Phys. Fluids 10(8), 1834 (1998). 10.1063/1.869703 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeong J. H., Sugii Y., Minamiyama M., and Okamoto K., Microvasc. Res. 71(3), 212 (2006). 10.1016/j.mvr.2006.02.006 [DOI] [PubMed] [Google Scholar]