Abstract
Phylogenetic tree reconciliation is a powerful approach for inferring evolutionary events like gene duplication, horizontal gene transfer, and gene loss, which are fundamental to our understanding of molecular evolution. While duplication–loss (DL) reconciliation leads to a unique maximum-parsimony solution, duplication-transfer-loss (DTL) reconciliation yields a multitude of optimal solutions, making it difficult to infer the true evolutionary history of the gene family. This problem is further exacerbated by the fact that different event cost assignments yield different sets of optimal reconciliations. Here, we present an effective, efficient, and scalable method for dealing with these fundamental problems in DTL reconciliation. Our approach works by sampling the space of optimal reconciliations uniformly at random and aggregating the results. We show that even gene trees with only a few dozen genes often have millions of optimal reconciliations and present an algorithm to efficiently sample the space of optimal reconciliations uniformly at random in O(mn2) time per sample, where m and n denote the number of genes and species, respectively. We use these samples to understand how different optimal reconciliations vary in their node mappings and event assignments and to investigate the impact of varying event costs. We apply our method to a biological dataset of approximately 4700 gene trees from 100 taxa and observe that 93% of event assignments and 73% of mappings remain consistent across different multiple optima. Our analysis represents the first systematic investigation of the space of optimal DTL reconciliations and has many important implications for the study of gene family evolution.
Key words: gene duplication, gene family evolution, gene-tree/species-tree reconciliation, horizontal gene transfer, host-parasite cophylogeny, phylogenetics
1. Introduction
The systematic comparison of a gene tree with its species tree under a reconciliation framework is a powerful technique for understanding gene family evolution. Specifically, gene tree/species tree reconciliation shows how the gene tree evolved inside the species tree while accounting for events like gene duplication, gene loss, and horizontal gene transfer, which drive gene family evolution. Thus, gene tree/species tree reconciliation is widely used and has many important applications, for example, for inferring orthologs, paralogs, and xenologs (Storm and Sonnhammer, 2002; Koonin, 2005; Wapinski et al., 2007; van der Heijden et al., 2007; Vilella et al., 2009; Sennblad and Lagergren, 2009; Mi et al., 2010); reconstructing ancestral gene content and dating gene birth (Chen et al., 2000; Ma et al., 2008; David and Alm, 2011), accurate gene tree reconstruction (Vilella et al., 2009; Rasmussen and Kellis, 2011), and whole genome species-tree reconstruction (Bansal et al., 2007; Burleigh et al., 2011).
Duplication–loss (DL) reconciliation, which accounts for only gene duplication and gene loss events, has been widely studied and extensively used (Goodman et al., 1979; Page, 1994; Mirkin et al., 1995; Eulenstein and Vingron, 1998; Bonizzoni et al., 2005; Durand et al., 2006; Górecki and Tiuryn, 2006; Chauve et al., 2008). However, since it does not account for horizontal gene transfer events, it only applies to multicellular eukaryotes, a very small part of the tree of life. An interesting and extremely useful property of DL-reconciliation is that, assuming loss events have a nonzero positive cost, the most parsimonious reconciliation is always unique (Górecki and Tiuryn, 2006). In addition, the most parsimonious reconciliation remains the same irrespective of the chosen event costs for duplication and loss. Given these properties, there is no ambiguity in interpreting the results of DL-reconciliation, which makes it extremely easy to use in practice.
The limited applicability of DL reconciliation has led to the formulation of the duplication-transfer-loss (DTL) reconciliation model, which can simultaneously account for duplication, transfer, and loss events and can be applied to species and gene families from across the entire tree of life. Indeed, the DTL-reconciliation model and its variants have been widely studied in the literature (Gorbunov and Liubetskii, 2009; Doyon et al., 2010; Tofigh, 2009; Tofigh et al., 2011; David and Alm, 2011; Chen et al., 2012; Bansal et al., 2012; Stolzer et al., 2012). In addition, DTL-reconciliation has also been indirectly studied in the context of the host–parasite cophylogeny problem (Charleston, 1998; Ronquist, 2003; Merkle and Middendorf, 2005; Libeskind-Hadas and Charleston, 2009; Merkle et al., 2010; Conow et al., 2010; Ovadia et al., 2011).
The DTL-reconciliation problem is typically solved in a parsimony framework, where costs are assigned to duplication, transfer, and loss events, and the goal is to find a reconciliation with minimum total cost. DTL-reconciliations can sometimes be time-inconsistent; that is the inferred transfers may induce contradictory constraints on the dates for the internal nodes of the species tree. The problem of finding an optimal time-consistent reconciliation is known to be NP-hard (Tofigh et al., 2011; Ovadia et al., 2011). Thus, in practice, the goal is to find an optimal (but not necessarily time-consistent) DTL-reconciliation. The problem of finding an optimal time-consistent reconciliation does become efficiently solvable (Libeskind-Hadas and Charleston, 2009; Doyon et al., 2010) if the species tree is fully dated. However, accurately dating the internal nodes of a species tree is a notoriously difficult problem (Rutschmann, 2006), which severely restricts its applicability. Thus, for wider applicability and efficient solvability, in this work, unless otherwise stated, we assume the input species tree is undated and seek an optimal (not necessarily time-consistent) DTL-reconciliation (Tofigh et al., 2011; David and Alm, 2011; Chen et al., 2012; Bansal et al., 2012). This problem can be solved very efficiently, with our own algorithm achieving the fastest known time complexity of O(mn) (Bansal et al., 2012), where m and n denote the number of nodes in the gene tree and species tree respectively.
Despite its extensive literature, the DTL-reconciliation problem remains difficult to use in practice for understanding gene family evolution. The first reason for this difficulty is that there are often multiple equally optimal reconciliations for a given gene tree and species tree and for a fixed assignment of event costs. The second reason is that event costs, which can be very difficult to assign confidently, play a much more important role than in DL reconciliation, as varying the costs can result in different optimal reconciliations.
Thus, when applying DTL-reconciliation in practice, it is unclear whether the evolutionary history implied by a particular given optimal solution is meaningful, as many other optimal reconciliations exist with the same minimal reconciliation cost. Moreover, it is unclear whether the properties of an optimal reconciliation are representative of the space of optimal reconciliations, and also how large and diverse this space is. Furthermore, the number of optimal reconciliations is often prohibitively large, as it can grow exponentially in the number of events required for the reconciliation, making even the basic task of enumerating all optimal reconciliations unfeasible for all but the smallest of gene trees (Chen et al., 2012). Here, we directly address these problems and seek to make DTL-reconciliation as easy to use as the DL-reconciliation model.
It was recently shown that, when the species tree is fully dated, one can represent the set of all optimal reconciliations in a compact way by building a polynomially-sized minimum reconciliation graph (Scornavacca et al., 2013). While this is an interesting approach to dealing with multiple optima, the fact that this is only known to work when the species tree is fully dated severely limits its applicability in practice. Moreover, since constructing the minimum reconciliation graph requires O(mn3) time and space (Scornavacca et al., 2013), where m and n denote the number of nodes in the gene tree and species tree, respectively, it can only be applied to small instances of the problem.
Our contribution. In this work, we develop an efficient and scalable approach to explore the space of optimal DTL-reconciliations and show how it can be used to infer the similarities and differences in the different optimal reconciliations for any given input instance. Our approach is based on uniformly random sampling of optimal reconciliations, and we demonstrate the utility of our approach by applying it to a biological dataset of approximately 4700 gene trees from 100 (predominantly prokaryotic) taxa (David and Alm, 2011). Specifically, our contributions are as follows:
1. We analyze the gene trees in the biological dataset and show that even gene trees with only a few dozen genes often have many millions of optimal reconciliations. This analysis provides the first detailed look into the prevalence of optimal reconciliations in biological datasets.
2. We study some basic structural properties of optimal DTL-reconciliations, which shed light on the inherent structure in optimal reconciliations and are both mathematically and biologically interesting.
3. We show how to efficiently sample the space of optimal reconciliations uniformly at random. Our algorithm produces each random sample in O(mn2) time and requires only O(mn) space, where m and n denote the number of nodes in the gene tree and species tree, respectively. This algorithm is fast enough to be applied thousands of times to the same dataset and scalable enough to be applied to datasets with hundreds or thousands of taxa.
4. We use our algorithm for random sampling to explore the space of optimal reconciliations and investigate the similarities and differences between the different optimal reconciliations. We show how to distinguish between the parts of the reconciliation that have high support from those that are more variable across the different multiple optima.
5. We show that even in the presence of multiple optimal solutions, a large amount of shared information can be extracted from the different optimal reconciliations. For instance, we observed that, for fixed event costs, any internal node taken from a gene tree in the biological dataset had a 93.31% chance of having the same event assignment (speciation, duplication, or transfer) and a 73.15% chance of being mapped to the same species tree node, across all (sampled) optimal reconciliations.
6. Our method allows users to compare the space of optimal reconciliations for different event costs and extract the shared aspects of the reconciliation. This makes it possible to study the impact of using different event costs and to meaningfully apply DTL-reconciliation even if one is unsure of the exact event costs to use. We applied our method to the biological dataset using different event costs and observed that large parts of the reconciliation tend to be robust to event cost changes.
Thus, our new method allows for large-scale, systematic exploration of the space of optimal reconciliations in real biological datasets and makes it possible to deal effectively with multiple optima by being able to distinguish between the parts of the reconciliation that have high support and those that are more variable across the different optimal reconciliations.
The remainder of the article is organized as follows: The next section introduces basic definitions and preliminaries. In Section 3, we study the prevalence of multiple optimal reconciliations in biological data, and in Section 4, the basic structural properties of optimal reconciliations. We introduce our sampling-based approach and algorithms in Section 5. The results of our analysis of the multiple optimal reconciliations for the biological dataset appear in Section 6, and in Section 7, we show how our method can be applied to study the impact of using different reconciliation costs. Concluding remarks appear in Section 8.
2. Definitions And Preliminaries
We follow the basic definitions and notation from Bansal et al. (2012). Given a tree T, we denote its node, edge, and leaf sets by V(T), E(T), and Le(T) respectively. If T is rooted, the root node of T is denoted by rt(T), the parent of a node 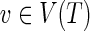 by paT (v), its set of children by ChT(v), and the (maximal) subtree of T rooted at v by T(v). If two nodes in T have the same parent, they are called siblings. The set of internal nodes of T, denoted I(T), is defined to be V(T)\Le(T). We define ≤T to be the partial order on V(T) where x≤T
y if y is a node on the path between rt(T) and x. The partial order ≥T is defined analogously, that is, x ≥ T
y if x is a node on the path between rt(T) and y. We say that v is an ancestor of u, or that u is a descendant of v, if u≤T
v (note that, under this definition, every node is a descendant as well as an ancestor of itself). We say that x and y are incomparable if neither u≤T
v nor v≤T
u. Given a nonempty subset L ⊆ Le(T), we denote by lcaT(L) the least common ancestor (LCA) of all the leaves in L in tree T ; that is, lcaT (L) is the unique smallest upper bound of L under ≤T. Given
by paT (v), its set of children by ChT(v), and the (maximal) subtree of T rooted at v by T(v). If two nodes in T have the same parent, they are called siblings. The set of internal nodes of T, denoted I(T), is defined to be V(T)\Le(T). We define ≤T to be the partial order on V(T) where x≤T
y if y is a node on the path between rt(T) and x. The partial order ≥T is defined analogously, that is, x ≥ T
y if x is a node on the path between rt(T) and y. We say that v is an ancestor of u, or that u is a descendant of v, if u≤T
v (note that, under this definition, every node is a descendant as well as an ancestor of itself). We say that x and y are incomparable if neither u≤T
v nor v≤T
u. Given a nonempty subset L ⊆ Le(T), we denote by lcaT(L) the least common ancestor (LCA) of all the leaves in L in tree T ; that is, lcaT (L) is the unique smallest upper bound of L under ≤T. Given 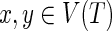 , x → T
y denotes the unique path from x to y in T. We denote by dT(x, y) the number of edges on the path x → T
y. Throughout this work, unless otherwise stated, the term “tree” refers to a rooted binary tree.
, x → T
y denotes the unique path from x to y in T. We denote by dT(x, y) the number of edges on the path x → T
y. Throughout this work, unless otherwise stated, the term “tree” refers to a rooted binary tree.
We assume that each leaf of the gene tree is labeled with the species from which that gene was sampled. This labeling defines a leaf-mapping
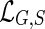 : Le(G) → Le(S) that maps a leaf node
: Le(G) → Le(S) that maps a leaf node 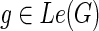 to that unique leaf node
to that unique leaf node 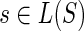 , which has the same label as g. Note that gene trees may have more than one gene sampled from the same species. Throughout this work, we denote the gene tree and species tree under consideration by G and S respectively and will implicitly assume that
, which has the same label as g. Note that gene trees may have more than one gene sampled from the same species. Throughout this work, we denote the gene tree and species tree under consideration by G and S respectively and will implicitly assume that 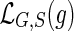 is well defined.
is well defined.
2.1. Reconciliation and DTL-scenarios
Reconciling a gene tree with a species tree involves mapping the gene tree into the species tree. Next, we define what constitutes a valid reconciliation; specifically, we define a duplication-transfer-loss scenario (DTL-scenario) (Tofigh et al., 2011; Bansal et al., 2012) for G and S that characterizes the mappings of G into S that constitute a biologically valid reconciliation. Essentially, DTL-scenarios map each gene tree node to a unique species tree node in a consistent way that respects the immediate temporal constraints implied by the species tree and designates each gene tree node as representing either a speciation, duplication, or transfer event.
Definition 2.1
(DTL-scenario). A DTL-scenario for G and S is a seven-tuple
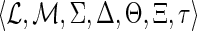 , where
, where
 : Le(G) → Le(S) represents the leaf-mapping from
G to
: Le(G) → Le(S) represents the leaf-mapping from
G to
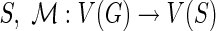 maps each node of G to a node of S, the sets Σ, Δ, and Θ partition I(G) into speciation, duplication, and transfer nodes respectively; Ξ is a subset of gene tree edges that represent transfer edges, and τ: Θ → V(S) specifies the recipient species for each transfer event, subject to the following constraints:
maps each node of G to a node of S, the sets Σ, Δ, and Θ partition I(G) into speciation, duplication, and transfer nodes respectively; Ξ is a subset of gene tree edges that represent transfer edges, and τ: Θ → V(S) specifies the recipient species for each transfer event, subject to the following constraints:
1. If
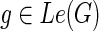 , then
, then
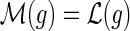 .
.-
2. If
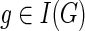 and g′ and g″ denote the children of g, then,
and g′ and g″ denote the children of g, then,(a)
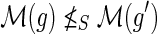 and
and
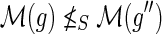 ,
,(b) At least one of
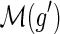 and
and
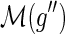 is a descendant of
is a descendant of
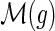 .
.
3. Given any edge
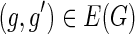 ,
,
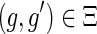 if and only if
if and only if
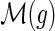 and
and
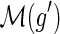 are incomparable.
are incomparable.-
4. If
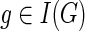 and g′ and g″ denote the children of g, then,
and g′ and g″ denote the children of g, then,(a)
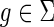 only if
only if
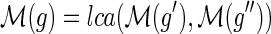 and
and
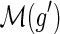 and
and
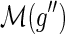 are incomparable,
are incomparable,(b)
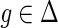 only if
only if
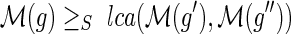 ,
,(c)
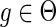 if and only if either
if and only if either
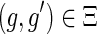 or
or
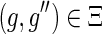 .
.(d) If
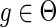 and
and
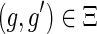 , then
, then
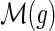 and τ(g) must be incomparable, and
and τ(g) must be incomparable, and
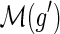 must be a descendant of τ(g), that is,
must be a descendant of τ(g), that is,
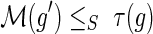 .
.
Constraint 1 above ensures that the mapping 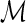 is consistent with the leaf-mapping
is consistent with the leaf-mapping  . Constraint 2(a) imposes on
. Constraint 2(a) imposes on  the temporal constraints implied by S. Constraint 2(b) implies that any internal node in G may represent at most one transfer event. Constraint 3 determines the edges of G that are transfer edges. Constraints 4(a), 4(b), and 4(c) state the conditions under which an internal node of G may represent a speciation, duplication, and transfer respectively. Constraint 4(d) specifies which species may be designated as the recipient species for any given transfer event.
the temporal constraints implied by S. Constraint 2(b) implies that any internal node in G may represent at most one transfer event. Constraint 3 determines the edges of G that are transfer edges. Constraints 4(a), 4(b), and 4(c) state the conditions under which an internal node of G may represent a speciation, duplication, and transfer respectively. Constraint 4(d) specifies which species may be designated as the recipient species for any given transfer event.
In some cases, one may wish to restrict transfer events to only occur between coexisting species. This requires that divergence time information (either absolute or relative) be available for all the internal nodes of the species tree. In such cases, the definition of a DTL-scenario remains the same, except for the additional restriction on transfer events.
DTL-scenarios correspond naturally to reconciliations, and it is straightforward to infer the reconciliation of G and S implied by any DTL-scenario. Figure 1 shows two simple DTL-scenarios. Given a DTL-scenario, one can directly count the minimum number of gene losses (Bansal et al., 2012) in the corresponding reconciliation as follows.
FIG. 1.
Multiple optimal reconciliations. Parts (a) and (b) show two different reconciliations for the gene tree and species tree depicted in the figure. Both of the reconciliations are optimal for event costs PΔ = 1, PΘ = 3, and Ploss = 1. The reconciliation in part (a) invokes one duplication, one transfer, and two losses, while the reconciliation in part (b) invokes two transfers.
Definition 2.2
(Losses). Given a DTL-scenario
 for G and S, let
for G and S, let
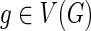 and {g′, g″} = Ch(g). The number of losses Lossα(g) at node g is defined to be:
and {g′, g″} = Ch(g). The number of losses Lossα(g) at node g is defined to be:
•
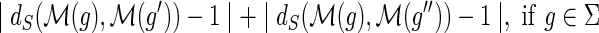
•
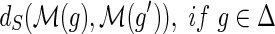 and
and
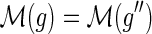 .
.•
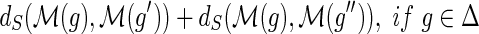 ,
,
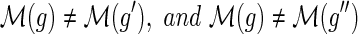 , and
, and•
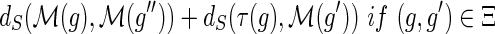 .
.
We define the total number of losses in the reconciliation corresponding to the DTL-scenario α to be
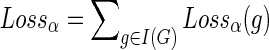 .
.
Let PΔ, PΘ, and Ploss denote the costs associated with duplication, transfer, and loss events respectively. The cost of reconciling G and S according to a DTL-scenario α is defined as follows.
Definition 2.3
(reconciliation cost of a DTL-scenario). Given a DTL-scenario
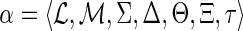 for G and S, the reconciliation cost associated with α is given by
for G and S, the reconciliation cost associated with α is given by
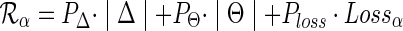 .
.
Given G and S, along with event costs PΔ, PΘ, and Ploss, the goal is to find a most parsimonious reconciliation of G and S. More formally,
Problem 1 (most parsimonious reconciliation, or MPR). Given G and S, the most parsimonious reconciliation (MPR) problem is to find a DTL-scenario for G and S with minimum reconciliation cost.
We distinguish two versions of the MPR problem: (i) the undated MPR (U-MPR) problem in which the species tree is undated, and (ii) the fully-dated MPR (D-MPR) problem in which every node of the species tree has an associated divergence time estimate (or there is a known total order on the internal nodes of the species tree), and transfer events are required to occur only between coexisting species.
Note that even if G and S are such that S contains one or more species that are not represented in G, we keep the species tree as is (i.e., we do not trim S to match the species set of G).
3. Multiple Optimal Solutions
In general, for any fixed values of PΔ, PΘ, and Ploss, there may be multiple equally optimal solutions to the MPR problem (both U-MPR and D-MPR). This is illustrated in Figure 1. The figure also illustrates the fundamental problem with having multiple optima: Given the different evolutionary histories implied by the different multiple optima, what is the true evolutionary history of the gene family? We address this problem in this article. But first, in this section, we investigate the prevalence of optimal reconciliations in real datasets. For our study, we use a published biological dataset of 4735 gene trees and 100 (predominantly prokaryotic) species (David and Alm, 2011). The gene trees in the dataset have median and average leaf-set sizes of 18 and 35.1, respectively. This dataset has been previously analyzed using DTL-reconciliation but without consideration of multiple optima. In our analysis of this dataset we used the same event costs as used by David and Alm (2011) (i.e., PΔ = 2, PΘ = 3, and Ploss = 1). Since the gene trees in the dataset are unrooted, we first rooted them optimally by choosing a root that minimized the reconciliation cost. In cases where there were multiple optimal rootings, we chose one of the optimal rootings at random. We computed the number of multiple optimal reconciliations for each of the rooted gene trees by augmenting the dynamic programming algorithm used to solve the MPR problem (e.g., Bansal et al. 2012) to keep track of the number of optima for each subproblem. Further algorithmic details appear in Section 5. Unless otherwise stated, all analyses in the manuscript were performed using the undated version of DTL-reconciliation (i.e., the U-MPR problem).
Figure 2 shows the results of our analysis. As part (a) of the figure shows, only 17% of the approximately 4700 gene trees have a unique optimal reconciliation. Over half of the gene trees have over 100 optimal reconciliations and 15% have more than 10,000 optimal reconciliations. This illustrates the extent of the problem with multiple optimal reconciliations in biological datasets. As part (b) of the figure shows, the number of optimal reconciliations tends to increase exponentially with gene tree size. These results demonstrate the importance of considering multiple optima in DTL-reconciliation, and the impracticality of enumerating all optimal reconciliations for all but the smallest gene trees.
FIG. 2.
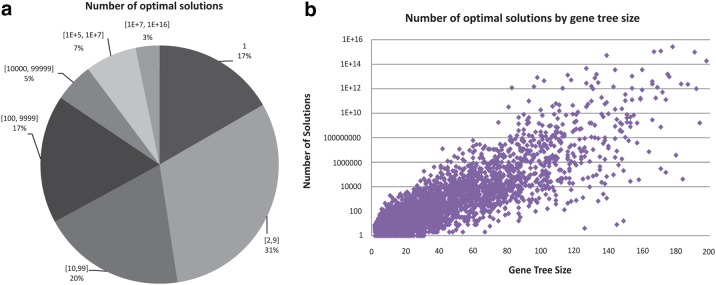
Number of optimal reconciliations for gene trees in the biological dataset. The pie chart in part (a) shows the distribution of the number of optimal reconciliations for the different gene trees in the biological dataset. The dot plot in part (b) plots the size (in the number of internal nodes) and the number of optimal reconciliations for each gene tree. Due to arithmetic overflow concerns, results are only shown for the 4699 (out of 4735) gene trees that had fewer than 1016 optima.
We also repeated the above analysis using the dated version of the DTL-reconciliation problem (i.e., the D-MPR problem), and observed no significant reduction in the number of multiple optima. For instance, even for the dated version, 14% of the gene trees had more than 10,000 optimal reconciliations. To make sure that the choice of event costs was not responsible for inflating the counts (since, in this case, PΘ = PΔ + Ploss, potentially making it easier to trade off transfers for duplications and losses), we also tried changing the event costs to 1.9, 2.9, and 0.9 for duplication, transfer, and loss, respectively, and observed only a small reduction in the numbers of inferred optimal reconciliations. Specifically, we observed that 11.6% of the gene trees still had over 10,000 optimal reconciliations, and 7.6% still had over 100,000 optimal reconciliations.
Recall that the gene trees in the dataset were originally unrooted. While the results above are for a fixed optimal rooting of these gene trees, we point out that about half the gene trees in the dataset have more than one optimal rooting. It may thus be necessary, in practice, to either consider all possible optimal rootings when studying multiple optimal reconciliations, or to use other information to assign a root uniquely.
4. Basic Structural Properties of Optimal Reconciliations
While there may be multiple optimal solutions for any given instance of the MPR problem, the gene tree–species tree mappings in optimal reconciliations are, as we show, strongly constrained. The following theorem applies to both the U-MPR and D-MPR problems.
Theorem 4.1.
Let g be any node in I(G) and g′, g″ be its two children. If loss events have a nonzero positive cost, then any optimal solution for the MPR problem on G and S must satisfy the following constraint: If
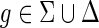 then
then
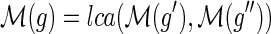 .
.
Proof
Let α denote any optimal reconciliation for G and S. Suppose, for the sake of contradiction, that α does not satisfy the constraint of part (1). Then, under the mapping of α, G must contain a node h ∈ Σα ∪ Δα such that 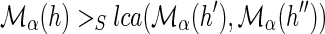 , where {h′, h″} = Ch(h). Let α′ denote an alternative DTL-scenario obtained from α by changing the mapping of h to
, where {h′, h″} = Ch(h). Let α′ denote an alternative DTL-scenario obtained from α by changing the mapping of h to 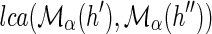 . Clearly, α′ is a valid DTL-scenario. We will show that α′ has a lower reconciliation cost than α, a contradiction.
. Clearly, α′ is a valid DTL-scenario. We will show that α′ has a lower reconciliation cost than α, a contradiction.
If 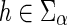 , then the constraint follows immediately from the definition of DTL-scenarios. Thus, assume that
, then the constraint follows immediately from the definition of DTL-scenarios. Thus, assume that 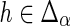 . Note that the number of transfers, duplications, and speciations is completely identical for α and α′. Consequently, any difference in the reconciliation costs of α and α′ must be purely due to different numbers of losses. Also observe that, if
. Note that the number of transfers, duplications, and speciations is completely identical for α and α′. Consequently, any difference in the reconciliation costs of α and α′ must be purely due to different numbers of losses. Also observe that, if 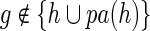 then Lossα(g) =Lossα′(g). Let
then Lossα(g) =Lossα′(g). Let 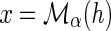 and
and 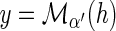 . Since
. Since 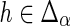 , it follows from the definition of losses that Lossα′(h) = Lossα(h)−2 × d(x, y). It also follows that Lossα′(pa(h)) ≤ Lossα(pa(h)) + d(x,y), irrespective of whether pa(h) is a speciation, duplication, or transfer. Since d(x,y) ≥ 1, it follows that
, it follows from the definition of losses that Lossα′(h) = Lossα(h)−2 × d(x, y). It also follows that Lossα′(pa(h)) ≤ Lossα(pa(h)) + d(x,y), irrespective of whether pa(h) is a speciation, duplication, or transfer. Since d(x,y) ≥ 1, it follows that 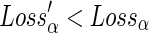 , which implies that α′ has a lower reconciliation cost than α. This contradicts the initial assumption that α is an optimal reconciliation. ■
, which implies that α′ has a lower reconciliation cost than α. This contradicts the initial assumption that α is an optimal reconciliation. ■
Similar observations were made by David and Alm (2011), who used the constraints on the mappings to speed up their algorithm for the MPR problem. However, they did not provide any proofs and erroneously assumed that the constraint on the mapping of speciation and duplication events also applies to transfer events; that is, if 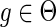 and
and 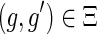 then
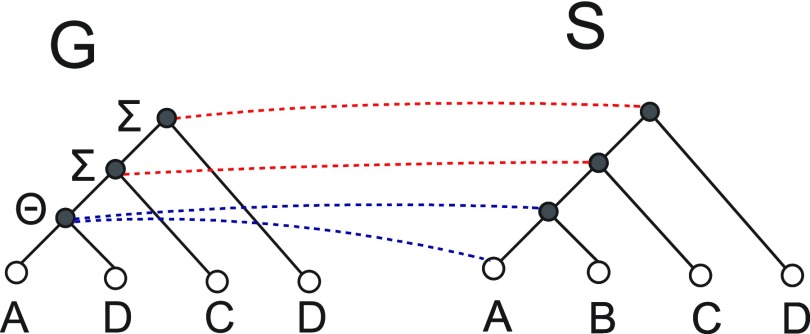
then 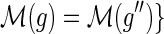 . As Figure 3 demonstrates, this does not hold true for transfer events.
. As Figure 3 demonstrates, this does not hold true for transfer events.
FIG. 3.
Mappings from transfer events. Assuming that transfers, duplications, and losses have an equal cost, any optimal reconciliation of G and S must have a cost of 2. The figure depicts two such optimal reconciliations, one in which the transfer node maps to species A and one in which it maps to the species represented by lca(A,B). These two mappings are shown by the dashed blue lines. All other nodes have identical mappings in the two reconciliations. Both reconciliations have one loss and one transfer, and the reconciliation in which the transfer node maps to lca(A,B) shows that transfer node mappings are not constrained in the manner of speciation or duplication nodes as shown in Theorem 4.1.
5. Uniformly Random Sampling of Optimal Reconciliations
As Section 3 demonstrates, the exhaustive enumeration of all optimal reconciliation is only feasible for very small gene trees. Indeed, as Figure 2 shows, even gene trees with only a few dozen taxa often have hundreds of millions of solutions, and this number grows exponentially with gene tree size. In this section, we show how to sample the space of reconciliations uniformly at random. Random sampling makes it possible to explore the space of optimal reconciliations without exhaustive enumeration and makes it possible to understand the variability in the different reconciliations and to distinguish between the highly supported and weakly supported parts of a given optimal reconciliation. Our algorithm for random sampling is based on the dynamic programming algorithm for the MPR problem from Bansal et al. (2012). The idea is to keep track of the number of optimal solutions for each subproblem considered in the dynamic programming algorithm. In the following, we show how to compute the number of optimal solutions at each step correctly and efficiently. First, we need a few definitions.
Given any 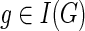 and
and 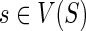 , let cΣ(g, s) denote the cost of an optimal reconciliation of G(g) with S such that g maps to s and
, let cΣ(g, s) denote the cost of an optimal reconciliation of G(g) with S such that g maps to s and 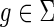 . The terms cΔ(g, s) and cΘ(g, s) are defined similarly for
. The terms cΔ(g, s) and cΘ(g, s) are defined similarly for 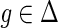 and
and 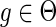 respectively. Given any
respectively. Given any 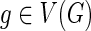 and
and 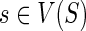 , we define c(g, s) to be the cost of an optimal reconciliation of G(g) with S such that g maps to s. The algorithm for the MPR problem performs a nested post-order traversal of the gene tree and species tree to compute the value of c(g, s) for each g and s. The dynamic programming table is initialized as follows for each
, we define c(g, s) to be the cost of an optimal reconciliation of G(g) with S such that g maps to s. The algorithm for the MPR problem performs a nested post-order traversal of the gene tree and species tree to compute the value of c(g, s) for each g and s. The dynamic programming table is initialized as follows for each 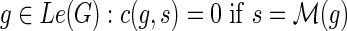 , and c(g, s) = ∞ otherwise. For
, and c(g, s) = ∞ otherwise. For 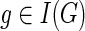 , observe that c(g, s) =min{cΣ(g,s), cΔ(g,s), cΘ(g,s)}.
, observe that c(g, s) =min{cΣ(g,s), cΔ(g,s), cΘ(g,s)}.
At each step, the values of cΣ(g, s), cΔ(g, s), and cΘ(g, s) for any 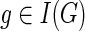 and
and 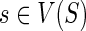 , can be computed based on the previously computed values of c(·,·). To show how cΣ(g, s), cΔ(g, s), and cΘ(g,s) are computed, we need some additional notation. Let
, can be computed based on the previously computed values of c(·,·). To show how cΣ(g, s), cΔ(g, s), and cΘ(g,s) are computed, we need some additional notation. Let 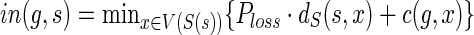 and
and 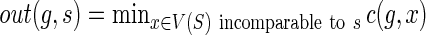 . In other words: out(g, s) is the cost of an optimal reconciliation of G(g) with S such that g may map to any node from V(S) that is incomparable to s; and in(g,s) is the cost of an optimal reconciliation of G(g) with S such that g may map to any node, say x, in V(S(s)) but with an additional reconciliation cost of one loss event for each edge on the path from s to x. The values cΣ(g,s), cΔ(g, s), and cΘ(g, s) are computed as follows:
. In other words: out(g, s) is the cost of an optimal reconciliation of G(g) with S such that g may map to any node from V(S) that is incomparable to s; and in(g,s) is the cost of an optimal reconciliation of G(g) with S such that g may map to any node, say x, in V(S(s)) but with an additional reconciliation cost of one loss event for each edge on the path from s to x. The values cΣ(g,s), cΔ(g, s), and cΘ(g, s) are computed as follows:
For any 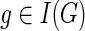 and
and 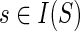 , let {g′, g″} = ChG(g) and {s′, s″} = ChS(s).
, let {g′, g″} = ChG(g) and {s′, s″} = ChS(s).
If 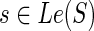 then,
then,
cΣ(g, s) = ∞ ,
cΔ(g, s) = PΔ + c(g′,s) + c(g″, s), and
if s ≠ rt(S), then cΘ(g, s) = PΘ + min{in(g′, s) + out(g″, s), in(g″, s) + out(g′, s)}. Else, cΘ(g, s) = ∞.
If 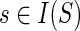 , then
, then
cΣ(g, s) = min{in(g′, s′) + in(g″, s″), in(g″,s′) + in(g′,s″)}.
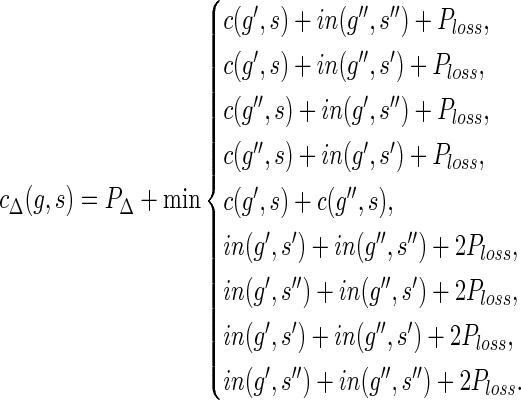 |
If s ≠ rt(S), then cΘ(g, s) = PΘ + min{in(g′, s) + out(g″, s), in(g″, s) + out(g′, s)}. Else, cΘ(g, s) = ∞.
The optimal reconciliation cost of G and S is simply: 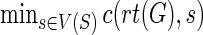 , and an optimal reconciliation with that cost can be reconstructed by backtracking in the dynamic programming table. We refer the reader to Bansal et al. (2012) for further algorithmic details.
, and an optimal reconciliation with that cost can be reconstructed by backtracking in the dynamic programming table. We refer the reader to Bansal et al. (2012) for further algorithmic details.
5.1. Computing the number of optimal reconciliations
To output optimal reconciliations uniformly at random we must keep track of the number of optimal reconciliations for each of the subproblems considered in the dynamic programming algorithm. We define the following: For any 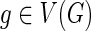 and
and 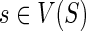 , let N(g, s) denote the number of optimal solutions for reconciling G(g) with S such that g maps to s. The idea is to compute N(·,·) using the same nested post-order traversal used to compute the c(·,·) values. The dynamic programming table for N(·,·) is initialized as follows for each
, let N(g, s) denote the number of optimal solutions for reconciling G(g) with S such that g maps to s. The idea is to compute N(·,·) using the same nested post-order traversal used to compute the c(·,·) values. The dynamic programming table for N(·,·) is initialized as follows for each 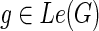 :
:
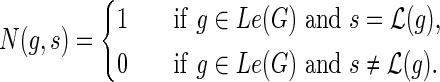 |
To compute N(g, s), for 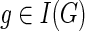 , we must consider all possible mappings of g′ and g″ that yield a cost of c(g, s). In the interest of brevity and clarity, let us assume that
, we must consider all possible mappings of g′ and g″ that yield a cost of c(g, s). In the interest of brevity and clarity, let us assume that 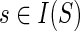 and s ≠ rt(S); the cases when
and s ≠ rt(S); the cases when 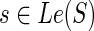 or s = rt(S) are easy to handle analogously.
or s = rt(S) are easy to handle analogously.
Let a1 through a13 denote the individual expressions in the min{ } blocks in the equations for cΣ(g, s), cΔ(g, s), and cΘ(g, s) above. Specifically, let a1 denote in(g′, s′) + in(g″, s″), a2 denote in(g″, s′) + in(g′, s″), a3 through a11 denote the nine expressions in the min{ } block for cΔ(g, s), and a12 and a13 denote the two expressions in the min{ } block for cΘ(g, s). Each of these ais represents a certain cost, which we denote by c(ai), and a certain number of optimal reconciliations, which we denote by N(ai). Furthermore, let bi, for 1 ≤ i ≤ 13, be binary boolean variables associated with the ais such that bi = 1 if ai yields the minimum cost c(g,s), and bi = 0 otherwise. Specifically, for 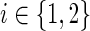 , bi = 1 if and only if c(ai) = c(g, s); for
, bi = 1 if and only if c(ai) = c(g, s); for 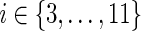 , bi = 1 if and only if c(ai) + PΔ = c(g, s); and for
, bi = 1 if and only if c(ai) + PΔ = c(g, s); and for 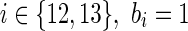 if and only if c(ai) + PΘ = c(g,s). Then, we must have:
if and only if c(ai) + PΘ = c(g,s). Then, we must have:
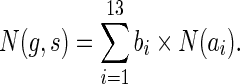 |
(1) |
Next, we show how to compute N(ai) for any i. Observe that each ai has one term involving g′ and one term involving g″. These terms take one of the three forms: c(·,·), in(·,·), or out(·,·). These terms, involving g′ and g″, can be viewed as representing the choice of optimal mappings for g′ and g″, respectively. For instance, c(g′, s) implies that g′ must map to s, in(g′, s) implies that g′ may map to any node 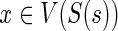 for which (Ploss · dS(s,x) + c(g′,x)) is minimized (recall the definition of in(·,·)), and out(g′,s) implies that g′ may map to any node
for which (Ploss · dS(s,x) + c(g′,x)) is minimized (recall the definition of in(·,·)), and out(g′,s) implies that g′ may map to any node 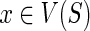 that is incomparable to s, for which c(g′,x) is minimized. Based on this observation, for any given ai, we can compute a set of optimal mappings for g′, which we will denote by X′ and a set of optimal mappings for g″, which we will denote by X″. It is not hard to see that the value of N(ai) must be as follows:
that is incomparable to s, for which c(g′,x) is minimized. Based on this observation, for any given ai, we can compute a set of optimal mappings for g′, which we will denote by X′ and a set of optimal mappings for g″, which we will denote by X″. It is not hard to see that the value of N(ai) must be as follows:
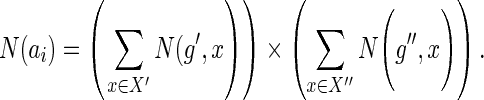 |
(2) |
Note that, for deriving the expression of N(g,s) above, we have assumed that 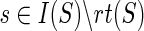 ; this is because the expression for at least one of cΣ(g, s), cΔ(g, s), or cΘ(g, s) changes when
; this is because the expression for at least one of cΣ(g, s), cΔ(g, s), or cΘ(g, s) changes when 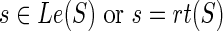 . The expressions for N(g, s), for
. The expressions for N(g, s), for 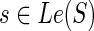 , and s = rt(S) can be derived similarly by simply accounting for these minor differences in the number of terms that constitute the sum on the R.H.S. of Equation 1. Specifically, when
, and s = rt(S) can be derived similarly by simply accounting for these minor differences in the number of terms that constitute the sum on the R.H.S. of Equation 1. Specifically, when 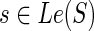 , the terms cΣ(g, s), cΔ(g, s), and cΘ(g, s) contribute 0, 1, and 2 ais, respectively. Thus, in this case, there are only three ais: a1 denotes c(g′, s) + c(g″, s), a2 denotes in(g′, s) + out(g″, s), and a3 denotes in(g″, s) + out(g′, s).
, the terms cΣ(g, s), cΔ(g, s), and cΘ(g, s) contribute 0, 1, and 2 ais, respectively. Thus, in this case, there are only three ais: a1 denotes c(g′, s) + c(g″, s), a2 denotes in(g′, s) + out(g″, s), and a3 denotes in(g″, s) + out(g′, s).
Similarly, when s = rt(S), the terms cΣ(g, s) and cΔ(g, s) contribute, as before, 2 and 9 ais, respectively, while cΘ(g, s) contributes none; this yields eleven ais, 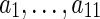 , that are identical to the first eleven ais used in Equation 1. Thus, the analogues of Equation 1 for the two cases when
, that are identical to the first eleven ais used in Equation 1. Thus, the analogues of Equation 1 for the two cases when 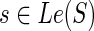 and s = rt(S) are, respectively:
and s = rt(S) are, respectively:
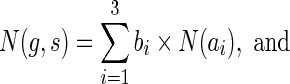 |
(3) |
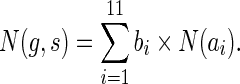 |
(4) |
The equations for N(g, s) and N(ai) derived above make it possible to compute the value N(g, s) for each 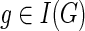 and
and 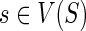 by using the same nested post-order traversal that is used for computing the values c(·,·). For completeness, a detailed description of the algorithm is given below as Procedure ComputeNumSolutions.
by using the same nested post-order traversal that is used for computing the values c(·,·). For completeness, a detailed description of the algorithm is given below as Procedure ComputeNumSolutions.
Procedure.
ComputeNumSolutions(G, S,
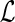 , PΣ, PΔ, PΘ)
, PΣ, PΔ, PΘ)
1: for each 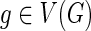 and and 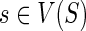 do do
|
| 2: Initialize c(g, s), cΣ(g, s), cΔ(g, s), and cΘ(g, s) to ∞, and N(g, s) to 0. |
3: for each 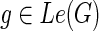 do do
|
4: Initialize c(g,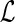 (g)) to 0, and N(g, (g)) to 0, and N(g,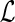 (g)) to 1. (g)) to 1. |
5: for each 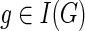 in post-order do in post-order do
|
6: for each 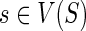 in post-order do in post-order do
|
| 7: Let {g′, g″} = ChG(g). |
8: if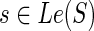 then then
|
| 9: cΣ(g, s) = ∞. |
| 10: cΔ(g, s) = PΔ + c(g′, s) + c(g″, s). |
| 11: cΘ(g, s) = PΘ + min{in(g′, s) + out(g″, s), in(g″, s) + out(g′, s)}. |
| 12: c(g, s) = min{cΣ(g, s), cΔ(g, s), cΘ(g, s)}. |
13: Assign the three ai expressions as described earlier (for the case when 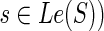 and, for each and, for each 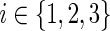 , compute N(ai) using Equation 2. , compute N(ai) using Equation 2. |
| 14: Compute N(g, s) using Equation 3. |
| 15: else |
| 16: Let {s′, s″} = ChS(s). |
| 17: cΣ(g, s) = min{in(g′, s′) + in(g″, s″), in(g″, s′) + in(g′, s″)}. |
18: 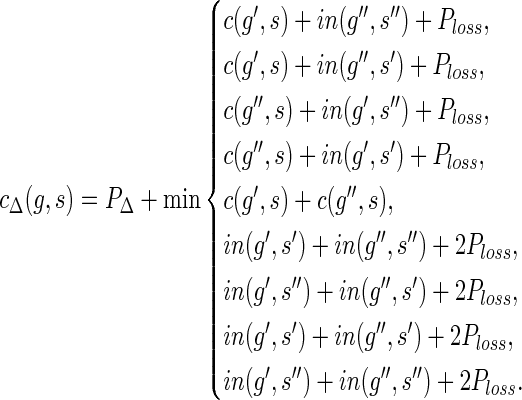
|
| 19: If s ≠ rt(S), then cΘ(g, s) = PΘ + min{in(g′, s) + out(g″, s), in(g″, s) + out(g′, s)}. |
| 20: c(g, s) = min{cΣ(g, s), cΔ(g, s), cΘ(g, s)}. |
| 21: ifs ≠ rt(S) then |
22: Assign the thirteen ai expressions as described earlier (for the case when 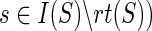 and compute N(ai), for each and compute N(ai), for each 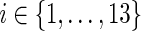 , using Equation 2. , using Equation 2. |
| 23: Compute N(g, s) using Equation 1. |
| 24: ifs = rt(S) then |
25: Assign the eleven ai expressions as described earlier (for the case when s = rt(S)) and compute N(ai), for each 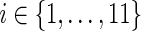 , using Equation 2. , using Equation 2. |
| 26: Compute N(g, s) using Equation 4. |
Let m and n denote the number of leaf nodes in G and S, respectively. We have the following:
Theorem 5.1.
Given G and S, and fixed event costs PΔ, PΘ, and Ploss, the value N(g, s) for
each
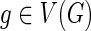 and
and
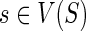 can be computed in O(mn2) time.
can be computed in O(mn2) time.
Proof
From Bansal et al. (2012) we already know that Procedure ComputeNumSolutions correctly computes each c(·,·). We will show that Procedure ComputeNumSolutions correctly computes each N(·,·) in O(mn2) time. ■
Correctness: Observe that the value of N(g,s) is initialized correctly for each 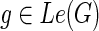 in the “for” loops of Steps 1 and 3. Let g be any node in I(G) and let {g′, g″} = ChG(g). Let us assume that the values N(g′, x) and N(g″, x) have been computed correctly for each
in the “for” loops of Steps 1 and 3. Let g be any node in I(G) and let {g′, g″} = ChG(g). Let us assume that the values N(g′, x) and N(g″, x) have been computed correctly for each 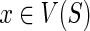 . We will show that the value of N(g, s), for any
. We will show that the value of N(g, s), for any 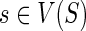 , is computed correctly as well.
, is computed correctly as well.
For some fixed g and s, consider any ai for which bi = 1 in the equation used to compute N(g,s) (i.e., in Eqs 1, 3, or 4). Let X′ and X″ be as defined for Equation 2, for this chosen ai. By definition, any mapping from g′ to a node in x′ and from g″ to a node in X″ yields an optimal solution with cost c(g,s) for the subproblem associated with the value N(g,s). Thus, the mapping of g′ represents exactly 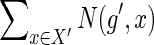 optimal reconciliations for the subproblem, while the mapping of g″ represents exactly
optimal reconciliations for the subproblem, while the mapping of g″ represents exactly 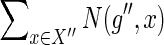 . Since the mappings of g′ and g″ can be assigned independently (for any fixed ai), the total number of optimal reconciliations for the subproblem must be exactly as given by Equation 2.
. Since the mappings of g′ and g″ can be assigned independently (for any fixed ai), the total number of optimal reconciliations for the subproblem must be exactly as given by Equation 2.
To complete the proof we must now also show the correctness of Equation 1 (the correctness of Eqs. 3 and 4 will follow trivially). It suffices to show that the terms chosen as part of the sum in the R.H.S. of Equation 1 (i.e., for which bi = 1) represent pairwise disjoint sets of reconciliations. Observe that the expressions for a3 through a7 and for a10 through a13 each represent a set of reconciliations that does not overlap with any other ai (due to different constraints on the mappings for at least one of g′ or g″). However, the expression for a1 matches the expression for a8, both of which restrict the mapping of g′ as in(g′, s′) and the mapping of g″ as in(g″, s″), and the expression for a2 matches the expression for a9, both of which restrict the mapping of g′ as in(g′, s″) and the mapping of g″ as in(g″, s′). However, since the terms a1 and a2 represent speciation while the terms a8 and a9 represent duplication, the lowest reconciliation costs for scenarios a1 and a2 will always be less than the lowest reconciliation costs for scenarios a8 and a9 (assuming that duplication and/or loss events have non zero positive costs). This implies that neither b8 nor b9 can ever be 1. Thus, the terms chosen as part of the sum in the R.H.S. of Equation 1 (i.e., for which bi = 1) must all represent pairwise disjoint sets of reconciliations.
Induction completes the proof.
Complexity: We analyze the complexity of Procedure ComputeNumSolutions step-by-step. The “for” loops from Steps 1 through 4 require O(mn) time. Steps 7 through 26 each require at most O(n) time and are each executed O(mn) times (through the “for” loops at lines 5 and 6), yielding a total time complexity of O(mn2) for these steps. The total time complexity of Procedure ComputeNumSolutions is thus O(mn2). ■
Corollary 5.1.
Given G and S, and fixed event costs PΔ, PΘ, and Ploss, the total number of optimal reconciliations of G and S can be computed in O(mn2) time.
Proof
Let μ denote the minimum reconciliation cost of G and S, and let Y denote the set 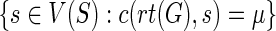 . Then, the total number of optimal reconciliations of G and S is simply
. Then, the total number of optimal reconciliations of G and S is simply 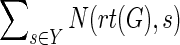 . Since all c(·,·) and all N(·,·) can be computed in O(mn2) time by Procedure ComputeNumSolutions (Theorem 5.1), the corollary follows. ■
. Since all c(·,·) and all N(·,·) can be computed in O(mn2) time by Procedure ComputeNumSolutions (Theorem 5.1), the corollary follows. ■
Remarks. (1) Note that the total number of optimal reconciliations can grow exponentially as a function of gene tree and species tree size. Throughout this work, however, when analyzing the time/space complexity of our algorithm, we make the assumption that the values N(·,·) can each be stored in some constant-sized memory block. (2) It is worth observing that the approach described above also makes it possible to compute the number of optimal reconciliations when the species tree is dated or, more generally, when constraints are imposed on the mappings or event assignments for some subset of the nodes of the gene tree.
5.2. Sampling optimal reconciliations uniformly at random
Once all the c(·,·) and N(·,·) have been computed, an optimal reconciliation itself can be built by backtracking through the dynamic programming table. To ensure that reconciliations are generated uniformly at random, the idea is to make the choice of mapping assignments based on the number of optimal solutions contained within each choice. For instance, if a node g has already been assigned a mapping, its two children g′ and g″ must be assigned mappings jointly based on their joint probability mass.
In general, to output a reconciliation we must assign a mapping and an event (speciation, duplication, or transfer) to each node of G (see Definition 2.1). (Technically, we are also required to assign the transfer edges, but this is trivially accomplished once the mapping and event assignments are in place.) To ensure that the output reconciliation is sampled uniformly at random from the space of all optima, we generate this mapping and event assignment as shown in Procedure RandomOptimalReconciliation below. This algorithm assumes that Procedure ComputeNumSolutions has already been executed. Let μ denote the minimum reconciliation cost of G and S.
Procedure.
RandomOptimalReconciliation
1: for each 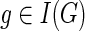 in a pre-order traversal of Gdo in a pre-order traversal of Gdo
|
| 2: ifg = rt(G) then |
3: Let P denote the set 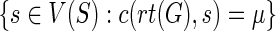 . . |
4: For any 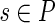 , assign the mapping , assign the mapping 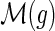 to be s with probability to be s with probability 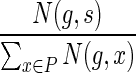 . . |
| 5: Let {g′, g″} = ChG(g). |
| 6: Let Q denote the set {i: bi = 1} in the context of the Equations 1, 3, or 4, used when computing N(g, s). |
7: Choose an ai, where 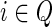 , with probability , with probability 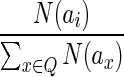 . . |
| 8: Assign an event type to g based on whether the chosen ai was derived from cΣ(·,·), cΔ(·,·), or cΘ(·,·). |
| 9: Consider the sets X′ and X″ for the chosen ai, as defined in Equation 2. |
10: Assign the mapping 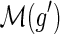 to be node s from X′ with probability to be node s from X′ with probability 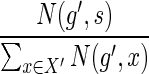 . . |
11: Assign the mapping 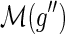 to be node s from X″ with probability to be node s from X″ with probability 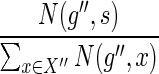 . . |
Steps 6 through 11 can actually be implemented during the nested post order traversal of Procedure ComputeNumSolutions for all possible 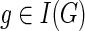 and
and 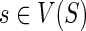 . This has the advantage of reducing the overall space complexity of the algorithm from O(mn2) to O(mn) since we need not store all the information about the ais and the X′ and X″, etc., for later reuse by Procedure RandomOptimalReconciliaton.
. This has the advantage of reducing the overall space complexity of the algorithm from O(mn2) to O(mn) since we need not store all the information about the ais and the X′ and X″, etc., for later reuse by Procedure RandomOptimalReconciliaton.
Based on the details of the procedure above, we have the following theorem.
Theorem 5.2.
Procedure RandomOptimalReconciliation generates each optimal reconciliation with equal probability.
Proof
Observe that the mapping assignment for g = rt(G) (Step 4) is consistent with the goal of generating each optimal reconciliation uniformly at random. We will prove the theorem by induction on the nodes of G. Consider some 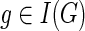 and suppose that the procedure fixes the mapping of g to some node s from V (S). It suffices to show that each optimal reconciliation of G(g) with S is now equally likely to be generated by the procedure, that is, each of those optimal reconciliations is generated with probability 1/N(g, s). By the proof of Theorem 5.1, we know that the ais, for
and suppose that the procedure fixes the mapping of g to some node s from V (S). It suffices to show that each optimal reconciliation of G(g) with S is now equally likely to be generated by the procedure, that is, each of those optimal reconciliations is generated with probability 1/N(g, s). By the proof of Theorem 5.1, we know that the ais, for 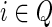 (Step 6), divide the reconciliations counted in N(g, s) into disjoint subsets. The procedure chooses one of these ais at random based on their probability mass and ensures that the generated reconciliation of G(g) with S is from the chosen ai (Steps 8 through 11). It remains to show that the procedure generates a reconciliation uniformly at random from among all the reconciliations that make up the chosen ai. Let {g′,g″} = ChG(g) and recall that the term ai consists of
(Step 6), divide the reconciliations counted in N(g, s) into disjoint subsets. The procedure chooses one of these ais at random based on their probability mass and ensures that the generated reconciliation of G(g) with S is from the chosen ai (Steps 8 through 11). It remains to show that the procedure generates a reconciliation uniformly at random from among all the reconciliations that make up the chosen ai. Let {g′,g″} = ChG(g) and recall that the term ai consists of 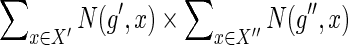 reconciliations (Eq. 2). To ensure a uniformly random generation of the reconciliations counted in ai, the mapping
reconciliations (Eq. 2). To ensure a uniformly random generation of the reconciliations counted in ai, the mapping 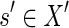 for g′ should be chosen with probability
for g′ should be chosen with probability 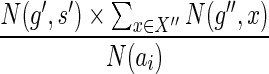 , which is equal to
, which is equal to 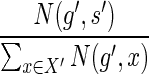 (by Eq. 2). Similarly, the mapping
(by Eq. 2). Similarly, the mapping 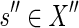 for g″ should be chosen with probability
for g″ should be chosen with probability 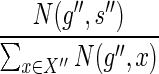 . Indeed, this is exactly how the procedure assigns the mappings of g′ and g″ in Steps 10 and 11. ■
. Indeed, this is exactly how the procedure assigns the mappings of g′ and g″ in Steps 10 and 11. ■
The overall time complexity of our algorithm for generating optimal reconciliations uniformly at random is dominated by that of Procedure ComputeNumSolutions and is consequently O(mn2). This is only a factor of n slower than the fastest known algorithm for the MPR problem (Bansal et al., 2012).
Our implementation of the random sampling algorithm will be made available as part of the next release of the RANGER-DTL software package (Bansal et al., 2012).
6. Exploring The Space Of Optimal Reconciliations
We applied our method to the biological dataset to understand the space of optimal reconciliations for the approximately 4700 gene trees in the dataset. As before, we used event costs PΔ = 2, PΘ = 3, and Ploss = 1 for this analysis. For this study, we focused on understanding how similar the different optimal reconciliations are to each other. To that end, we used our algorithm to sample 500 optimal reconciliations for each gene tree and wrote a program that reads in these samples and summarizes them as follows: For each internal node in the gene tree we (i) consider the fraction of times that node is mapped to the different nodes of the species tree, and (ii) consider the fraction of times that node is labeled as a speciation, duplication, and transfer event. We used this to investigate the stability of the embedding of the gene tree into the species tree (i.e., the stability of gene node mappings), and the stability of event assignments for the internal nodes of the gene tree.
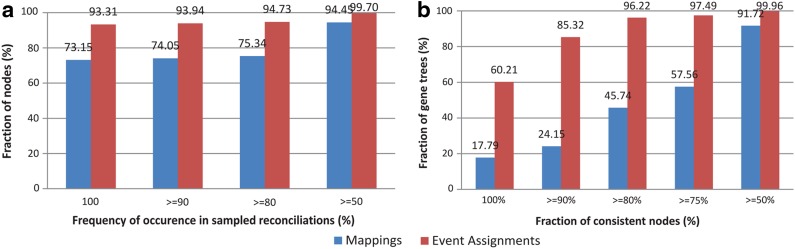
We first checked to see how stable the gene node mappings were across the internal nodes in all 4699 gene trees. Figure 4a shows the results of this analysis. Overall, we observed that mappings tended to be fairly well conserved across the different multiple optima. For instance, we observed that 73.15% of the internal gene tree nodes had the same mapping across all 500 samples. Recall that only 17% of the gene trees have a unique solution. We also repeated this analysis for event assignments and these results are also shown in Figure 4a. Amazingly, we observed that 93.31% of the nodes had a consistent event assignment across all 500 samples. This suggests that event assignments tend to be highly conserved across the different multiple optima. Thus, even in those instances where there are many different optimal reconciliations, it should be possible to confidently assign event types to most internal nodes of the gene tree (even though the mappings of the nodes themselves may not be consistent across the different multiple optima). This has important implications for understanding gene family evolution, since the inference of orthologs, paralogs, and xenologs depends only on the event assignments for gene tree nodes.
FIG. 4.
Stability of mappings and event assignments. The plot in part (a) shows the fraction of internal nodes from the 4699 gene trees that have the same mapping or the same event assignment across at least a certain fraction of the 500 samples. The plot in part (b) plots the fraction of the 4699 gene trees that have at least a certain fraction of their nodes with a consistent mapping or a consistent event assignment across all 500 samples.
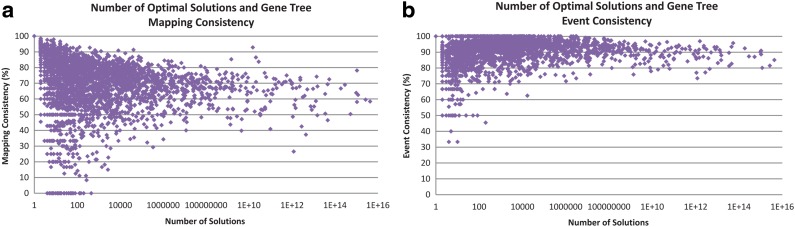
In practice, users are often interested in analyzing the evolutionary history of a specific gene family. We thus asked the following question: Given a gene tree from the biological dataset, what fraction of its nodes can be expected to have (i) a consistent mapping, and (ii) a consistent event assignment across all 500 samples. Figure 4b shows the results of this analysis. The results show that for most gene trees, event assignments are completely consistent across all samples for most of their internal nodes. For instance, we observed that 60.2% of the gene trees have a consistent event assignment for all of their internal nodes, and almost all gene trees had a consistent event assignment for at least half of their internal nodes. As we observed before, gene tree node mappings tend to be more variable, but still, over 91% of the gene trees had a consistent mapping for at least half of their internal nodes. We also tested to see if there was a correlation between the number of optimal reconciliations for a gene tree and fraction of its internal nodes with consistent mappings or consistent event assignments. To our surprise, we found no correlation (Fig. 5). Thus, even if a gene tree/species tree pair have many optimal reconciliations, a large fraction of the gene tree nodes can still be expected to have consistent mappings and event assignments.
FIG. 5.
Consistency of mappings and event assignments by number of optimal reconciliations. (a) Fraction of gene tree nodes that have a consistent mapping across all 500 samples. (b) Fraction of gene tree nodes that have a consistent event assignment across all 500 samples.
It is worth noting that our analysis of this entire ∼4700 gene tree, 100-taxon dataset, with 500 computed optimal reconciliations for each gene tree, required only about a week of running time on a desktop computer using a single 3 GHz processing core and 4 GB of RAM.
We also analyzed the stability of the mappings and assignments using the dated version of the DTL-reconciliation problem (i.e., the D-MPR problem) and obtained similar results. Specifically, we observed that for the dated version, 72.4% and 94.8% of the internal nodes has consistent mapping and event assignments, respectively, in each of the 100 random samples we tested. Thus, the additional restriction on transfers imposed when a fully dated species tree is used appears to have little effect on the consistency of assignments and mappings.
7. Application To Understanding Sensitivity To Event Costs
The ability to explore the space of multiple optimal reconciliations makes it possible to study the effect of using different event costs on the reconciliation. For instance, one can compare if the mapping or event assignments that are consistent across the multiple optima for a particular event cost assignment are also consistent across a different event cost assignment. Similarly, if one is unsure of which event cost assignment to use, one can try out several different event costs, compute a set of random samples for each event cost assignment, and aggregate the samples from all event cost assignments into a single analysis to understand which aspects of the reconciliation are conserved across the different event cost assignments.
We performed a preliminary study of the effect of using different event costs on the analysis of the biological dataset. Recall that our default event costs are PΔ = 2, PΘ = 3, and Ploss = 1. For this study, we kept Ploss = 1 but considered the following combinations of the duplication and transfer costs: (i) PΔ = 2, PΘ = 4, (ii) PΔ = 2, PΘ = 2, (iii) PΔ = 3, PΘ = 3, and (iv) PΔ = 1, PΘ = 1. We computed 100 random samples for each setting of event costs.
We first tested the impact of different cost assignments on the number of inferred speciation, duplication, and transfer events. Since the number of inferred events can vary across the different optimal reconciliations, even for the same fixed event cost assignment, we only considered those event assignments that are supported by all 100 samples (500 samples in case of the default cost assignment). Table 1 shows the results of our analysis. As expected, we observe that as the relative cost of a transfer event or duplication event increases, the number of inferred transfers or duplications, respectively, decreases. For instance, when the event cost assignment is changed from PΔ = 2 and PΘ = 3 to PΔ = 2, PΘ = 4, the number of transfers decreases from 62540 to 56217, with a corresponding increase in the number of speciations and duplications. Note also that the total number of speciations, duplications, and transfers with 100% support is significantly smaller for the cost assignments PΔ = 2 and PΘ = 2, and PΔ = 1 and PΘ = 1, than for the other cost assignments, indicating more variability in the reconciliations.
Table 1.
Impact of Event Costs on Event Inference
| Event type | PΔ = 2 PΘ = 3 |
PΔ = 2 PΘ = 2 |
PΔ = 2 PΘ = 4 |
PΔ = 3 PΘ = 3 |
PΔ = 1 PΘ = 1 |
|---|---|---|---|---|---|
| Speciation | 69174 | 64473 | 70582 | 70762 | 49973 |
| Duplication | 16501 | 12796 | 19813 | 12970 | 12385 |
| Transfer | 62540 | 67191 | 56217 | 65006 | 71977 |
This table shows the number of inferred speciation, duplication, and transfer events (inferred consistently across all random samples) for the different event cost assignments.
Next, we tested the impact of different cost assignments on the number of optimal reconciliations. Table 2 shows the results of our analysis. Note that the number of optimal reconciliations increases significantly for the cost assignments PΔ = 2 and PΘ = 2, and PΔ = 1 and PΘ = 1, compared to the other cost assignments. This is likely related to the observation made above that the total number of speciations, duplications, and transfers with 100% support is significantly smaller for these two cost assignments than for the others.
Table 2.
Impact of Event Costs on Number of Optimal Reconciliations.
| Number of optimal reconciliations | PΔ = 2 PΘ = 3 |
PΔ = 2 PΘ = 2 |
PΔ = 2 PΘ = 4 |
PΔ = 3 PΘ = 3 |
PΔ = 1 PΘ = 1 |
|---|---|---|---|---|---|
| 1 | 16.7% | 13.1% | 17.8% | 15.6% | 8.3% |
| [2, 9] | 30.9% | 25.7% | 30.6% | 28.0% | 19.8% |
| [10, 99] | 19.5% | 20.7% | 19.7% | 20.1% | 21.1% |
| [100, 9999] | 17.4% | 20.1% | 16.3% | 19.4% | 20.8% |
| [10000, 99999] | 5.3% | 6.4% | 4.9% | 5.6% | 7.2% |
| [105, 1016] | 10.2% | 14.0% | 10.7% | 11.3% | 22.8% |
This table shows the fraction (%) of gene trees for which the number of optimal reconciliations lies within the given ranges, for different event cost assignments.
Finally, we considered the following question: What fraction of the gene tree nodes with consistent mappings (event assignments) under the default costs also have the same consistent mappings (respective event assignments) under the alternative event costs? The results of this analysis for the four combinations of event costs listed above are as follows: For mappings, the fractions are 94%, 83.38%, 92.04%, and 63.97%, respectively. And, for event assignments, the fractions are 92.06%, 91.52%, 96.07%, and 80.37%, respectively. As the analysis indicates, consistent mappings and event assignments tend to be well conserved even when using different event costs. Even with the rather extreme event costs of PΔ = PΘ = Ploss = 1, almost 64% of the consistent mappings and over 80% of the event assignments are conserved.
8. Conclusion
In this work, we have presented an efficient and scalable approach to the problem of multiple optimal DTL-reconciliations. Our approach is based on random sampling, and we show how to sample the space of optimal reconciliations uniformly at random, efficiently in O(mn2) time per sample. The sampling-based approach makes it possible for users to explore the space of optimal reconciliations and to distinguish between stable and unstable parts of the reconciliation. This approach also allows users to investigate the effect of using different event costs on the reconciliation. Our analysis of the biological dataset provides the first real insight into the space of multiple optima and reveals that many, if not most, aspects of the reconciliation remain consistent across the different multiple optima, and that these can be efficiently inferred and used for understanding gene family evolution. We believe that this work represents an important step toward making DTL-reconciliation a practical method for understanding gene family evolution.
Many aspects of the space of optimal reconciliations remain to be explored. For instance, it would be interesting to investigate why so many of the input instances have millions (and more) of multiple optima. In this work, we did not consider the effect of alternative optimal gene tree rootings on the reconciliation space, and we would like to study this further. The ability to handle multiple optima also enables the systematic evaluation of the accuracy of DTL-reconciliation at inferring evolutionary history correctly, and we plan to pursue this further. It would also be instructive to study the effect of using different event costs more thoroughly. In our work, we have only considered optimal reconciliations, and it might be beneficial to also consider slightly suboptimal reconciliations; doing so in a principled way might require the use of a probabilistic model of gene family evolution by duplication, transfer, and loss (e.g., Tofigh, 2009).
Acknowledgments
This work was supported by a National Science Foundation CAREER award 0644282 to M.K., National Institutes of Health grant RC2 HG005639 to M.K., and National Science Foundation AToL grant 0936234 to E.J.A. and M.K.
Author Disclosure Statement
No competing financial interests exist.
References
- Bansal M.S. Burleigh J.G. Eulenstein O. Wehe A. Heuristics for the gene-duplication problem: A Θ(n) speed-up for the local search. RECOMB. 2007:238–252. [Google Scholar]
- Bansal M.S. Alm E.J. Kellis M. Efficient algorithms for the reconciliation problem with gene duplication, horizontal transfer and loss. Bioinformatics. 2012;28:283–291. doi: 10.1093/bioinformatics/bts225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonizzoni P. Vedova G.D. Dondi R. Reconciling a gene tree to a species tree under the duplication cost model. Theor. Comput. Sci. 2005;347:36–53. [Google Scholar]
- Burleigh J.G. Bansal M.S. Eulenstein O., et al. Genome-scale phylogenetics: Inferring the plant tree of life from 18,896 gene trees. Syst. Biol. 2011;60:117–125. doi: 10.1093/sysbio/syq072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charleston M. Jungles: A new solution to the host-parasite phylogeny reconciliation problem. Mathematical Biosciences. 1998;149:191–223. doi: 10.1016/s0025-5564(97)10012-8. [DOI] [PubMed] [Google Scholar]
- Chauve C. Doyon J.-P. El-Mabrouk N. Gene family evolution by duplication, speciation, and loss. J. Comput. Biol. 2008;15:1043–1062. doi: 10.1089/cmb.2008.0054. [DOI] [PubMed] [Google Scholar]
- Chen K. Durand D. Farach-Colton M. Notung: dating gene duplications using gene family trees. RECOMB. 2000:96–106. doi: 10.1089/106652700750050871. [DOI] [PubMed] [Google Scholar]
- Chen Z.-Z. Deng F. Wang L. Simultaneous identification of duplications, losses, and lateral gene transfers. IEEE/ACM Trans. Comput. Biology Bioinform. 2012;9:1515–1528. doi: 10.1109/TCBB.2012.79. [DOI] [PubMed] [Google Scholar]
- Conow C. Fielder D. Ovadia Y. Libeskind-Hadas R. Jane: a new tool for the cophylogeny reconstruction problem. Algorithm. Mol. Biol. 2010;5:16. doi: 10.1186/1748-7188-5-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- David L.A. Alm E.J. Rapid evolutionary innovation during an archaean genetic expansion. Nature. 2011;469:93–96. doi: 10.1038/nature09649. [DOI] [PubMed] [Google Scholar]
- Doyon J.-P. Scornavacca C. Gorbunov K.Y., et al. An efficient algorithm for gene/species trees parsimonious reconciliation with losses, duplications and transfers. In: Tannier E., editor. Springer; New York: 2010. pp. 93–108. RECOMB-CG, Vol. 6398 of Lecture Notes in Computer Science. [Google Scholar]
- Durand D. Halldórsson B.V. Vernot B. A hybrid micro-macroevolutionary approach to gene tree reconstruction. J. Comput. Biol. 2006;13:320–335. doi: 10.1089/cmb.2006.13.320. [DOI] [PubMed] [Google Scholar]
- Eulenstein O. Vingron M. On the equivalence of two tree mapping measures. Discrete Applied Mathematics. 1998;88:101–126. [Google Scholar]
- Goodman M. Czelusniak J. Moore G.W., et al. Fitting the gene lineage into its species lineage. a parsimony strategy illustrated by cladograms constructed from globin sequences. Systematic Zoology. 1979;28:132–163. [Google Scholar]
- Gorbunov K.Y. Liubetskii V.A. Reconstructing genes evolution along a species tree. Molekuliarnaia Biologiia. 2009;43:946–958. [PubMed] [Google Scholar]
- Górecki P. Tiuryn J. Dls-trees: A model of evolutionary scenarios. Theor. Comput. Sci. 2006;359:378–399. [Google Scholar]
- Koonin E.V. Orthologs, paralogs, and evolutionary genomics. Annual Review of Genetics. 2005;39:309–338. doi: 10.1146/annurev.genet.39.073003.114725. [DOI] [PubMed] [Google Scholar]
- Libeskind-Hadas R. Charleston M. On the computational complexity of the reticulate cophylogeny reconstruction problem. J. Comput. Biol. 2009;16:105–117. doi: 10.1089/cmb.2008.0084. [DOI] [PubMed] [Google Scholar]
- Ma J. Ratan A. Raney B.J., et al. Dupcar: Reconstructing contiguous ancestral regions with duplications. J. Comput. Biol. 2008;15:1007–1027. doi: 10.1089/cmb.2008.0069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merkle D. Middendorf M. Reconstruction of the cophylogenetic history of related phylogenetic trees with divergence timing information. Theory of Biosciences. 2005;123:277–299. doi: 10.1016/j.thbio.2005.01.003. [DOI] [PubMed] [Google Scholar]
- Merkle D. Middendorf M. Wieseke N. A parameter-adaptive dynamic programming approach for inferring cophylogenies. BMC Bioinformatics. 2010;11((Suppl 1)):S60. doi: 10.1186/1471-2105-11-S1-S60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mi H. Dong Q. Muruganujan A., et al. Panther version 7: improved phylogenetic trees, orthologs and collaboration with the gene ontology consortium. Nucleic Acids Research. 2010;38((suppl 1)):D204–D210. doi: 10.1093/nar/gkp1019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirkin B. Muchnik I. Smith T.F. A biologically consistent model for comparing molecular phylogenies. J. Comput. Biol. 1995;2:493–507. doi: 10.1089/cmb.1995.2.493. [DOI] [PubMed] [Google Scholar]
- Ovadia Y. Fielder D. Conow C. Libeskind-Hadas R. The cophylogeny reconstruction problem is np-complete. J. Comput. Biol. 2011;18:59–65. doi: 10.1089/cmb.2009.0240. [DOI] [PubMed] [Google Scholar]
- Page R.D.M. Maps between trees and cladistic analysis of historical associations among genes, organisms, and areas. Syst. Biol. 1994;43:58–77. [Google Scholar]
- Rasmussen M.D. Kellis M. A bayesian approach for fast and accurate gene tree reconstruction. Molecular Biology and Evolution. 2011;28:273–290. doi: 10.1093/molbev/msq189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ronquist F. Parsimony analysis of coevolving species associations. In: Page R. D. M., editor. Tangled Trees: Phylogeny, Cospeciation and Coevolution. The University of Chicago Press; Chicago: 2003. pp. 22–64. [Google Scholar]
- Rutschmann F. Molecular dating of phylogenetic trees: A brief review of current methods that estimate divergence times. Divers. Distrib. 2006;12:35–48. [Google Scholar]
- Scornavacca C. Paprotny W. Berry V. Ranwez V. Representing a set of reconciliations in a compact way. J Bio Comp Biol. 2013;11:1250025. doi: 10.1142/S0219720012500254. [DOI] [PubMed] [Google Scholar]
- Sennblad B. Lagergren J. Probabilistic orthology analysis. Syst. Biol. 2009;58:411–424. doi: 10.1093/sysbio/syp046. [DOI] [PubMed] [Google Scholar]
- Stolzer M. Lai H. Xu M., et al. Inferring duplications, losses, transfers and incomplete lineage sorting with nonbinary species trees. Bioinformatics. 2012;28:409–415. doi: 10.1093/bioinformatics/bts386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storm C.E.V. Sonnhammer E.L.L. Automated ortholog inference from phylogenetic trees and calculation of orthology reliability. Bioinformatics. 2002;18:92–99. doi: 10.1093/bioinformatics/18.1.92. [DOI] [PubMed] [Google Scholar]
- Tofigh A. Using Trees to Capture Reticulate Evolution : Lateral Gene Transfers and Cancer Progression [Ph.D. thesis] KTH Royal Institute of Technology; Stockholm: 2009. [Google Scholar]
- Tofigh A. Hallett M.T. Lagergren J. Simultaneous identification of duplications and lateral gene transfers. IEEE/ACM Trans. Comput. Biology Bioinform. 2011;8:517–535. doi: 10.1109/TCBB.2010.14. [DOI] [PubMed] [Google Scholar]
- van der Heijden R. Snel B. van Noort V. Huynen M. Orthology prediction at scalable resolution by phylogenetic tree analysis. BMC Bioinformatics. 2007;8:83. doi: 10.1186/1471-2105-8-83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vilella A.J. Severin J. Ureta-Vidal A., et al. Ensemblcompara genetrees: Complete, duplication-aware phylogenetic trees in vertebrates. Genome Research. 2009;19:327–335. doi: 10.1101/gr.073585.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wapinski I. Pferrer A. Friedman N. Regev A. Natural history and evolutionary principles of gene duplication in fungi. Nature. 2007;449:54–61. doi: 10.1038/nature06107. [DOI] [PubMed] [Google Scholar]