Procedure.
ComputeNumSolutions(G, S,
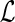 , PΣ, PΔ, PΘ)
, PΣ, PΔ, PΘ)
1: for each 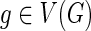 and and 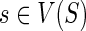 do do
|
| 2: Initialize c(g, s), cΣ(g, s), cΔ(g, s), and cΘ(g, s) to ∞, and N(g, s) to 0. |
3: for each 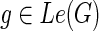 do do
|
4: Initialize c(g,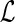 (g)) to 0, and N(g, (g)) to 0, and N(g,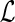 (g)) to 1. (g)) to 1. |
5: for each 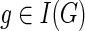 in post-order do in post-order do
|
6: for each 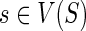 in post-order do in post-order do
|
| 7: Let {g′, g″} = ChG(g). |
8: if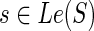 then then
|
| 9: cΣ(g, s) = ∞. |
| 10: cΔ(g, s) = PΔ + c(g′, s) + c(g″, s). |
| 11: cΘ(g, s) = PΘ + min{in(g′, s) + out(g″, s), in(g″, s) + out(g′, s)}. |
| 12: c(g, s) = min{cΣ(g, s), cΔ(g, s), cΘ(g, s)}. |
13: Assign the three ai expressions as described earlier (for the case when 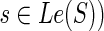 and, for each and, for each 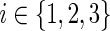 , compute N(ai) using Equation 2. , compute N(ai) using Equation 2. |
| 14: Compute N(g, s) using Equation 3. |
| 15: else |
| 16: Let {s′, s″} = ChS(s). |
| 17: cΣ(g, s) = min{in(g′, s′) + in(g″, s″), in(g″, s′) + in(g′, s″)}. |
18: 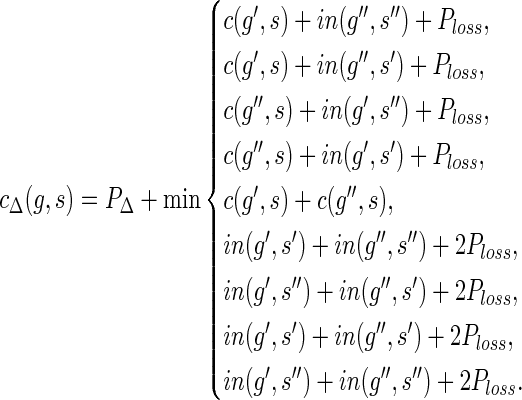
|
| 19: If s ≠ rt(S), then cΘ(g, s) = PΘ + min{in(g′, s) + out(g″, s), in(g″, s) + out(g′, s)}. |
| 20: c(g, s) = min{cΣ(g, s), cΔ(g, s), cΘ(g, s)}. |
| 21: ifs ≠ rt(S) then |
22: Assign the thirteen ai expressions as described earlier (for the case when 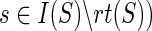 and compute N(ai), for each and compute N(ai), for each 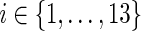 , using Equation 2. , using Equation 2. |
| 23: Compute N(g, s) using Equation 1. |
| 24: ifs = rt(S) then |
25: Assign the eleven ai expressions as described earlier (for the case when s = rt(S)) and compute N(ai), for each 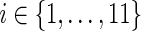 , using Equation 2. , using Equation 2. |
| 26: Compute N(g, s) using Equation 4. |
