Figure 1. Schematic representation of the problem and of our inference framework.
(A) A total of n identical objects (in gray, n = 50 in this example) is homogeneously dispersed in a finite volume V. A fraction r of V, having volume rV, is sampled (dashed red rectangle) and the number of object therein, denoted with k (k = 4 in this example) is determined. Given the measurement, the posterior distribution of n is a negative binomial probability distribution 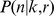 (bottom) computed from a binomial likelihood
(bottom) computed from a binomial likelihood 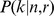 (right) and a discrete uniform prior P(n) (left). (B) Generalization of (A) to m measurements. Fractions of volume
(right) and a discrete uniform prior P(n) (left). (B) Generalization of (A) to m measurements. Fractions of volume  are sampled the number of objects therein (
are sampled the number of objects therein ( ) determined as before. However, when m>1 two cases can be distinguished: i) the fractions are replaced (sampling with replacement); ii) the fractions are removed from V (sampling without replacement). In both cases, we derived a formula for the posterior distribution which is reported in the text as equation 6 for case i and equation 10 for case ii.
) determined as before. However, when m>1 two cases can be distinguished: i) the fractions are replaced (sampling with replacement); ii) the fractions are removed from V (sampling without replacement). In both cases, we derived a formula for the posterior distribution which is reported in the text as equation 6 for case i and equation 10 for case ii.

