Effect of Specimen-Specific Anisotropic Material Properties in Quantitative Computed Tomography-Based Finite Element Analysis of the Vertebra

Short abstract

Intra- and inter-specimen variations in trabecular anisotropy are often ignored in quantitative computed tomography (QCT)-based finite element (FE) models of the vertebra. The material properties are typically estimated solely from local variations in bone mineral density (BMD), and a fixed representation of elastic anisotropy (“generic anisotropy”) is assumed. This study evaluated the effect of incorporating specimen-specific, trabecular anisotropy on QCT-based FE predictions of vertebral stiffness and deformation patterns. Orthotropic material properties estimated from microcomputed tomography data (“specimen-specific anisotropy”), were assigned to a large, columnar region of the L1 centrum (n = 12), and generic-anisotropic material properties were assigned to the remainder of the vertebral body. Results were compared to FE analyses in which generic-anisotropic properties were used throughout. FE analyses were also performed on only the columnar regions. For the columnar regions, the axial stiffnesses obtained from the two categories of material properties were uncorrelated with each other (p = 0.604), and the distributions of minimum principal strain were distinctly different (p ≤ 0.022). In contrast, for the whole vertebral bodies in both axial and flexural loading, the stiffnesses obtained using the two categories of material properties were highly correlated (R²> 0.82, p < 0.001) with, and were no different (p > 0.359) from, each other. Only moderate variations in strain distributions were observed between the two categories of material properties. The contrasting results for the columns versus vertebrae indicate a large contribution of the peripheral regions of the vertebral body to the mechanical behavior of this bone. In companion analyses on the effect of the degree of anisotropy (DA), the axial stiffnesses of the trabecular column (p < 0.001) and vertebra (p = 0.007) increased with increasing DA. These findings demonstrate the need for accurate modeling of the peripheral regions of the vertebral body in analyses of the mechanical behavior of the vertebra.

1. Introduction

Osteoporosis is a disease characterized by a loss of bone mass and deterioration in trabecular architecture, leading to decreased bone strength and increased susceptibility to fracture [1]. Vertebral fractures account for more than half of the approximately 1.5 million osteoporotic fractures that occur each year in the United States [2], heightening the need for accurate, noninvasive estimates of vertebral strength and stiffness. Quantitative computed tomography-based finite element models are increasingly used for noninvasive determination of mechanical properties of vertebrae [3,4], as they provide better predictions of vertebral strength compared to methods currently used in clinical diagnosis [5]. However, the material properties in the QCT-based FE models are typically estimated solely from local variations in bone mineral density [6,7] despite evidence that the biomechanical behavior of the vertebra depends also on the architecture of the vertebral trabecular bone [8,9], that the architecture is spatially inhomogeneous [10], and that the architecture is altered with age [11]. Advances in QCT imaging allow measurement of some architectural parameters [12,13], such as trabecular anisotropy [14], at clinically permissible doses of radiation. However, whether the effect of incorporating architectural information on the accuracy of the model predictions is large enough to warrant the additional model complexity and radiation exposure has not been established.

Anisotropy of the trabecular architecture is believed to result from adaption of bone to its mechanical environment (Wolff's law). Trabecular anisotropy, represented by the principal orientation of the trabecular network and by the degree of anisotropy, is influential in the mechanical behavior of vertebra [8]. With an increase in DA due to aging and osteoporosis [11,15], the number of horizontal trabeculae reduces, rendering the vertebra less capable of withstanding unusual or off-axis loads and also more prone to buckling under axial compressive loads [16]. Prior QCT-based, FE models of the vertebra, which were based solely on BMD, have assumed a constant DA and have had the principal direction always aligned with the superior-inferior (SI) direction [4,6,7] and, thus, may fail to capture differences in the biomechanical response of vertebrae with different trabecular architectures.

Variations in anisotropy within and among vertebrae can be accounted for using morphology-based constitutive models [17–19]. Recent studies that have incorporated one of these types of constitutive models as well as explicit modeling of the cortical shell in high-resolution peripheral QCT (HR-pQCT)-based FE models of vertebrae have shown combined effects of these additions on predictions of vertebral stiffness and locations of damage accumulation [20,21]. Accurate, explicit modeling of the shell is not possible at present using QCT in the axial skeleton; however, a realistic representation of the specimen-specific trabecular anisotropy alone would potentially improve the accuracy of QCT-based FE models of the vertebra.

The overall goal of this study was to evaluate the importance of incorporating specimen-specific trabecular anisotropy for QCT-based FE predictions of vertebral stiffness. The major aims of this study were: (1) to compare the QCT-based FE results obtained with fixed, anisotropic material properties (“generic-anisotropic”) for trabecular bone to those obtained with specimen-specific, anisotropic material properties and (2) to study the influence of DA on the FE predictions of vertebral stiffness. The FE models were evaluated under loading conditions of axial compression, pure anterior bending, and combined loading of axial compression and anterior bending (Fig. 1).

Fig. 1.

List of the FE analyses conducted to evaluate the effect of incorporating specimen-specific, trabecular anisotropy on QCT-based FE predictions of vertebral stiffness and deformation patterns: For each combination of type of model, type of material property, and loading condition, 12 simulations were performed (one per vertebra), for a total of 336 FE simulations performed in this study

2. Materials and Methods

2.1. Specimen Preparation and Imaging

2.1.1. QCT Imaging.

Twelve L1 spine segments (age 80.5 ± 8.65, six female, six male) with adjacent intervertebral disks were harvested from fresh-frozen spines by making a transverse cut just above the inferior endplate of T12 and below the superior endplate of L2. The spine segments were scanned using a 64-row detector system (GE Lightspeed VCT, GE Healthcare, Waukesha, WI) with the following acquisition parameters: 120 kV, 240 mA, pixel size of 0.3125 mm × 0.3125 mm, and slice thickness of 0.625 mm. The specimens were held in an acrylic fixture to ensure the slices were in the transverse anatomic plane of the specimen with the fixture submerged in a container filled with degassed water. A calcium hydroxyapatite calibration phantom (Image Analysis, Columbia, KY) was included in each scan to correct for scanner drift and for the estimation of bone mineral density.

2.1.2. Microcomputed Tomography (μCT) Imaging.

The μCT images of these vertebrae were obtained as part of another ongoing study in our laboratory. For that study, each of the spine segments was placed in a custom-designed, radiolucent, loading device. After ten cycles of preconditioning to 400 N, the L1 vertebra was scanned via μCT (μCT 80, Scanco Medical, Brüttisellen, Switzerland) with the following acquisition parameters: 70 kV, 114 mA, 300 ms integration time, and isotropic voxel size of 37 μm.

2.2. Creation of Vertebral Geometry.

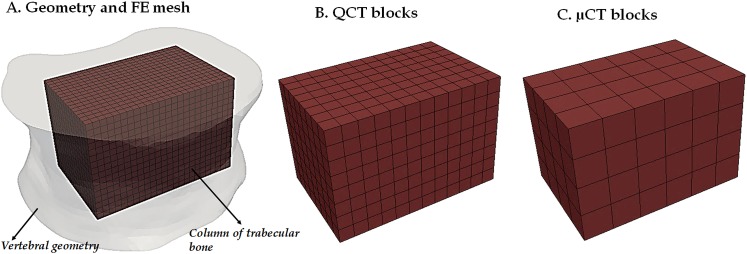
The QCT images were imported into AMIRA (Amira 5.2, Visage Imaging, Inc., San Diego, CA), and the external surface of the vertebral body was defined and converted to a set of contours (DXF file) by using a semi-automated segmentation technique. The plane of the images corresponded to the geometric x-y plane, the z-axis corresponded to the superior-inferior direction, and the origin was set to the top left corner of the first slice of the stack. A solid geometric representation of the vertebra was created in RHINOCEROS (Rhinoceros 4.0, Robert McNeel and Associates, Seattle, WA), exported from RHINOCEROS as a SAT file (Fig. 2(a)), and was directly imported into the ABAQUS preprocessor (Abaqus v6.8, SIMULIA, Providence, RI) to create the FE model [22]. The vertebral geometry was meshed using quadratic, tetrahedral elements in ABAQUS.

Fig. 2.

(a) Development of the finite element model of vertebra and (b) mapping of material properties into the FE model using the generic-anisotropic and specimen-specific, anisotropic material properties (vertebral geometry is shown in gray in the top row). As with the specimen-specific anisotropic material properties, the DA-based material properties are also mapped for only the regions covered by the μCT block model.

2.3. Determination of Material Properties

2.3.1. Generic Anisotropy.

For each of the 12 vertebrae, multiple cubic blocks of size 2.5 mm × 2.5 mm × 2.5 mm (Fig. 2(b)), collectively called the “QCT blocks” [22], were defined from the segmented QCT images. The blocks were created adjacent to one another using an in-house matlab script and mapped the entire vertebra, including the trabecular centrum as well as the vertebral endplates and the cortical shell (mean number of blocks per vertebra = 1518.00, maximum = 2133, minimum = 1119). The mineral density of a given block was obtained by averaging the intensities for all the voxels within the block. The average intensities were converted to equivalent values of bone mineral density (in mg/cm³) using the calibration phantom. The equivalent bone mineral density was converted to elastic modulus along the SI direction using the following experimentally determined relationship [23]

$$E_{\mathit{zz}}=-34.7+3.230{\rho }_{\mathrm{QCT}}$$ (1)

where E_zz is the elastic modulus in the SI direction (MPa) and ρ _QCT is the bone mineral density in mg/cm³. Any negative modulus obtained from the above relationship was converted to a preset value of 0.1 kPa. The remaining, orthotropic elastic properties were determined by assuming the following ratios and values [24,25]

$$\begin{array}{c}\multicolumn{1}{c}{\frac{E_{\mathit{xx}}}{E_{\mathit{zz}}}=0.333,\hspace{1em}\frac{E_{\mathit{yy}}}{E_{\mathit{zz}}}=0.333\frac{G_{\mathit{xy}}}{E_{\mathit{zz}}}=0.121,\hspace{1em}\frac{G_{\mathit{xz}}}{E_{\mathit{zz}}}=0.157,\hspace{1em}\frac{G_{\mathit{yz}}}{E_{\mathit{zz}}}=0.157{\nu }_{\mathit{xy}}=0.381,\hspace{1em}{\nu }_{\mathit{xz}}=0.104,\hspace{1em}{\nu }_{\mathit{yz}}=0.104}\end{array}$$ (2)

2.3.2. Specimen-Specific Anisotropy.

For each of the 12 vertebrae, multiple cubic blocks of size 5.0 mm × 5.0 mm × 5.0 mm, collectively called the “μCT blocks,” were created from the μCT images (Fig. 2(b)). The blocks were contiguous with one another and were selected to comprise the largest rectangular column that could fit within the trabecular centrum (mean number per vertebra = 70.75, maximum = 100, minimum = 45). This column did not include the cortical shell and endplates. The block size satisfied the continuum assumptions for the trabecular bone [26]. Each of the blocks was segmented using a global threshold value of 15% of the maximum gray value on a 16-bit scale (0.15 × 2¹⁵= 4915) and filtered using a Gaussian filter (σ = 0.8, and support = 1) (IPL, Scanco Medical, Brüttisellen, Switzerland). The global threshold value was obtained using an adaptive, iterative method [27]. Bone volume fraction, degree of anisotropy, and eigenvalues and eigenvectors of the fabric tensor [17,28] were determined for each of the linear blocks (IPL, Scanco Medical, Brüttisellen, Switzerland). Orthotropic, linear elastic material properties along the principal directions of the fabric ellipsoid (constructed from measurements of mean intercept length [29,30]) were calculated for the blocks using Cowin's morphology-elasticity constitutive model [17]

$$\begin{array}{l}{C}_{iiii}=E_{\text{tissue}}(k_1+2k_6+\left(k_2+2k_7\right)II+2\left(k_3+2k_8\right)H_i\\ +\left(2k_4+k_5+4k_9\right)H_i^2)\\ C_{iijj}=E_{\text{tissue}}\left(k_1+k_{2}II+k_3\left(H_i+H_j\right)+k_4\left(H_i^2+H_i^2\right)+k_5{H}_i{H}_j\right)\\ C_{ijij}=E_{\text{tissue}}\left(k_6+k_{7}II+k_8\left(H_i+H_j\right)+k_9\left(H_i^2+H_i^2\right)\right)\\ II=H_1{H}_2+H_2{H}_3+H_3{H}_1\\ k_i=k_{ia}+k_{ib}{\left(BV/TV\right)}^p,i=1,\mathrm{...},9,p=1.6\\ H_1>H_2>H_3,H_1+H_2+H_3=1\end{array}$$ (3)

where E _tissue is the tissue modulus (GPa), H_i is the normalized fabric eigenvalue, BV/TV is the bone volume fraction, II is the second invariant of the fabric tensor, and (k _ia, k _ib) are constants. The values of the constants (k _ia, k _ib) were taken from Kabel et al. [31] and the elastic modulus of the vertebral tissue was assumed to be 13 GPa [32]. The orthotropic material properties were then checked for satisfaction of thermodynamic constraints [33]. If the material properties for a block violated any one or more of these constraints, the bone volume fraction of the block was artificially increased beyond the measured value in increments of 0.0025 until all thermodynamic constraints were satisfied.

2.3.3. Parametric Variation of the Degree of Anisotropy.

To study the influence of the DA on the FE results, five different sets of transversely isotropic material properties, each corresponding to a DA of 1.09, 1.26, 1.43, 1.60, and 1.77 were defined for the μCT block model of each of the 12 vertebrae. These values of DA correspond to −2, −1, 0, 1, and 2 standard deviations from the mean DA (1.43) reported for trabecular bone from the human lumbar vertebra [34]. Transversely isotropic material properties were determined for each of the μCT blocks for different values of DA using Cowin's [17] morphology-elasticity relationship (Eq. (3)). The volume fraction for the μCT blocks was obtained from the μCT images (IPL, Scanco Medical, Brüttisellen, Switzerland). The normalized fabric eigenvalues for a given DA were calculated using the relationships DA = H ₁/H ₃, H ₂ = H ₃, and H ₁ + H ₂ + H ₃ = 1. It was assumed that the principal directions of the transversely isotropic properties were aligned along the geometric axes of the vertebra. The transversely isotropic material properties were checked for the satisfaction of thermodynamic constraints. It was observed that as the DA increased, the number of μCT blocks failing the thermodynamic constraints also increased. Thus, the following methodology was adopted in the determination of the material properties using different DA values.

The material properties were derived in a decreasing order of the DA starting from 1.77 using the volume fraction obtained from the μCT images. These properties were then checked against the thermodynamic constraints. If any of the properties violated a constraint, then the bone volume fraction was artificially increased beyond the measured value in increments of 0.0025 until the constraints were satisfied. The updated bone volume fraction was then assigned to the linear block for the determination of material properties using subsequent values of DA. The above steps were then repeated for the remaining values of DA.

2.4. Assignment of Material Properties.

The finite element model of each of the 12 vertebrae was assigned three different categories of material properties (Fig. 2(b)): (a) generic-anisotropic material properties; (b) specimen-specific, anisotropic material properties; and (c) DA-based material properties (Fig. 1). These categories corresponded to the categories of material properties described in Secs. 2.3.1–2.3.3, respectively. The generic-anisotropic material properties were mapped from the material properties derived using the density-elasticity relationships (Eqs. (1) and (2)) for the QCT-block model. The mapping was carried out using a centroid-based mapping algorithm [22]. Some of the finite elements on the edges of the geometric model do not have corresponding points in the QCT-block model due to the coarse nature of the QCT-block model. These elements were identified, and the material properties of the nearest elements (as defined by the distance between element centroids) with the centroid within the QCT-based block were assigned to these elements (Fig. 2(b), bottom left). The specimen-specific, anisotropic material properties were mapped from the morphology-elasticity relationships (Eq. (3)) for the μCT-block model. For the finite elements that were outside the μCT-block model, material properties prescribed for the element using the generic-anisotropic material properties were assigned (Fig. 2(b), bottom right). The DA-based material properties were mapped from the morphology-elasticity relationships (Eq. (3)) for the μCT-block model for the specified value of DA. This mapping was done separately for each of the five values of DA.

2.5. Finite Element Analyses of a Column of the Trabecular Centrum.

In the FE models of vertebra with the specimen-specific, anisotropic material properties, finite elements outside the μCT block were assigned generic-anisotropic material properties. Therefore, the results from the FE analysis using the specimen-specific, anisotropic material properties would have contributions from both the generic and specimen-specific, anisotropic material properties. To isolate the effect of the latter properties, an FE model of the rectangular column of trabecular bone was created out of the centrum of each of the vertebrae (Fig. 1, Fig. 3(a)). The columns were meshed using hexahedral elements 1.25 mm in length. The number of hexahedral elements per vertebrae varied from 2880 to 6400 with a mean of 4528. The FE models of the column were then assigned generic-anisotropic and, subsequently, specimen-specific, anisotropic material properties determined from the QCT- and μCT-block models, respectively (Figs. 3(b) and 3(c)).

Fig. 3.

(a) Depicted for one of the 12 vertebrae is the finite element mesh of the columnar region of trabecular bone, shown within the vertebral body for the purpose of demonstrating the column's location within the centrum. (b) the QCT blocks used for mapping of the generic-anisotropic material properties; (c) the μCT blocks used for mapping of the specimen-specific, anisotropic material properties.

Each FE model of a trabecular column was subjected to an axial compression by applying a uniform, downward displacement of 0.2 mm at the superior surface of the column (Abaqus v6.8, SIMULIA, Providence, RI). Displacement in the vertical direction at the inferior surface of the column was constrained. The total reaction force at the inferior surface of the column was determined from the FE analyses. Axial stiffness of the column was calculated by dividing the total reaction force at the inferior surface with the applied displacement on the superior surface. Distributions of minimum principal strain from the FE models using the generic-anisotropic and the specimen-specific, anisotropic material properties were also plotted and compared for each of the columns. The distribution of minimum principal strain is often used to identify regions of potential onset of fracture [35], with smaller (i.e., more compressive) values of minimum principal strain corresponding to greater risk of fracture.

2.6. Finite Element Analyses of the Vertebra.

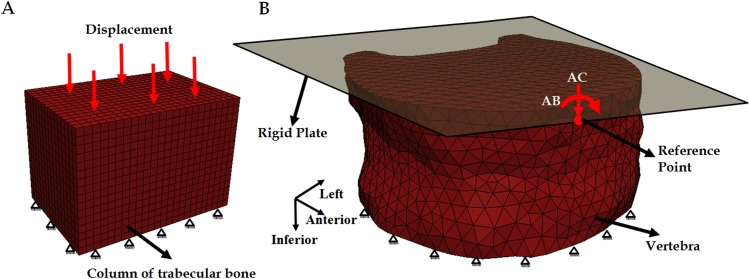
Finite element analyses were carried out on each of the 12 models of the entire vertebra using the generic-anisotropic; specimen-specific, anisotropic; and DA-based material properties (Fig. 1). The loading conditions on the FE model were applied via a rigid plate (modeled as an analytically rigid body) tied to the superior surface of the vertebra (Fig. 4). A reference point, which acts as the single node for the rigid body, was defined on the rigid plate at a distance of 30 mm from the plate center along the x-axis. The plate center nearly coincided with the geometric center of the superior surface.

Fig. 4.

Finite element model of (a) a column of trabecular bone and (b) vertebra with the rigid plate attached to the superior surface of the vertebra showing the force and boundary conditions applied to the reference point for axial compression (AC) and anterior bending (AB). The reference point was constrained to move only in the vertical direction under AC. For both types of loading, the inferior surfaces of the column and the vertebra were constrained in all directions.

Axial compression, anterior bending, and combined axial compression and anterior bending were implemented on the FE model. Axial compression was implemented by applying a compressive force (1000 N) on the reference point while constraining the rigid plate to move only in the vertical direction. Anterior bending (30 Nm) was simulated by applying a bending moment along the x-direction (Fig. 4(b)) at the reference point of the rigid plate. The displacement at the reference point was not constrained in any direction. Combined loading of axial compression and bending moment was applied through a compressive load on the reference point and without any displacement constraints. The superior surface was not allowed to expand with loading, and the displacement in the inferior surface was fully constrained in all directions.

Linear, static analyses were performed (Abaqus 6.8, SIMULIA, Providence, RI) on all the FE models. From the analyses, axial stiffness was computed by dividing the applied compressive force by the displacement of the rigid plate, and the bending stiffness was computed by dividing the applied moment by the rotation of the rigid plate in the direction corresponding to the bending moment. The distributions and directions of minimum principal strain using the generic-anisotropic and specimen-specific, anisotropic material properties were also plotted for each of the vertebrae. The directions of the principal strains were used as an indicator of the paths of load transfer throughout the vertebra and the principal directions of the trabecular structure (fabric eigenvectors) were also plotted.

2.7. Statistical Analysis.

Linear regression analyses and paired t-tests were performed to compare the FE predicted stiffnesses between the two categories of material properties, generic anisotropic and specimen-specific, anisotropic (JMP Pro 9.0.0, SAS Institute, Inc., Cary, NC), in order to understand the influence of nonuniform trabecular architecture on the mechanical behavior of the vertebra. Paired t-tests were also used to compare the minimum principal strains (on an element-by-element basis within each vertebra) predicted by the FE analysis with these two categories of material properties. For the FE analysis using the DA-based material properties, repeated-measures analyses of variance were used to compare the axial stiffness of the trabecular columns, and the axial and bending stiffnesses and the lowest (i.e., most compressive) minimum principal strain of the vertebrae among the DA values.

3. Results

3.1. Finite Element Analysis (FEA) of the Column of Trabecular Bone

3.1.1. Axial Stiffness.

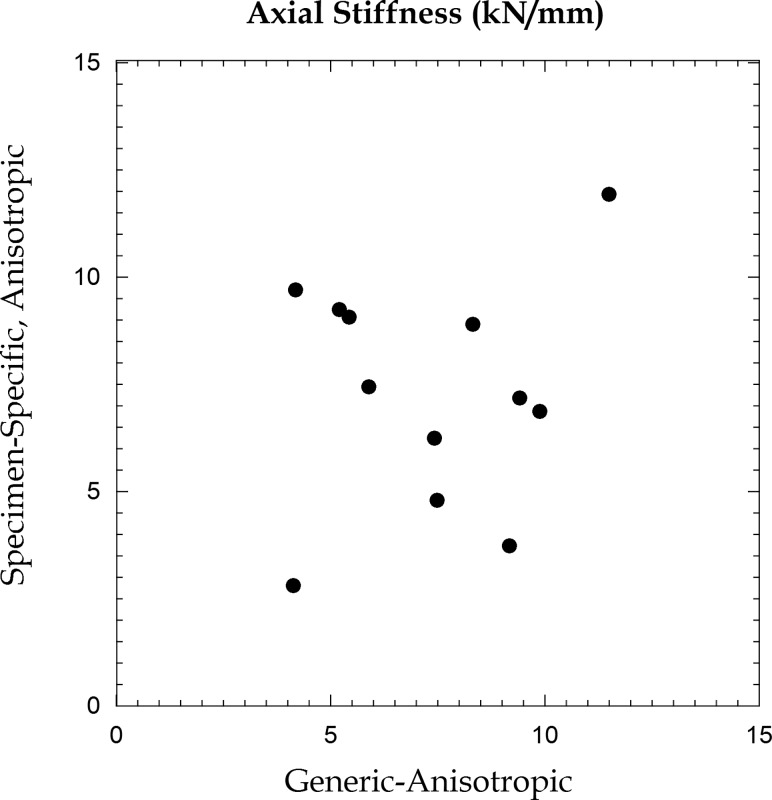
For the FE models of the columnar region of the trabecular centrum, no differences in axial stiffness were found between the generic-anisotropic and specimen-specific, anisotropic material properties (p = 0.987) (Table 1). However, the statistical power for this calculation was low (0.05), and no correlation was observed between the two sets of values (p = 0.605, Fig. 5).

Table 1.

FE predicted stiffness (mean ± standard deviation for the 12 vertebrae) obtained using the generic-anisotropic and specimen-specific, anisotropic material properties

	Generic-anisotropic	Specimen-specific, anisotropic
Column of trabecular bone:
Axial stiffness (kN/mm)	7.34 ± 2.39	7.32 ± 2.65
Vertebra:
Axial stiffness (kN/mm)	16.09 ± 5.52	16.24 ± 5.07
Bending stiffness (MNmm/rad)	1.48 ± 0.61	1.51 ± 0.60

Fig. 5.

Axial stiffness obtained from finite element analyses of the column using generic-anisotropic and specimen-specific, anisotropic material properties

3.1.2. Distribution of Minimum Principal Strain.

Both the magnitudes (p = 0.022 for the comparison of average strain and p < 0.001 for the element-by-element comparison) and spatial distributions of minimum principal strains differed between the two material properties (Table 2, Fig. 6). Regions of high strain predicted by the FE simulations with the specimen-specific, anisotropic material property did not have correspondingly high strains with the generic-anisotropic material property. The principal orientations of the elastic modulus, which were aligned with the anatomic axes in the FE models with the generic-anisotropic property but not necessarily in the FE models with the specimen-specific, anisotropic material property, were observed to influence the directions of principal strain (Fig. 7).

Table 2.

Difference in the minimum principal strains obtained from the finite element analysis using the generic-anisotropic and specimen-specific, anisotropic material properties: For each of the 12 vertebrae, the median of the element-by-element differences between the minimum principal strains computed using generic versus specimen-specific anisotropic material properties was computed. Listed in the table are the median, minimum, and maximum of those 12 values for each loading case.

	Median	Minimum	Maximum
Column of trabecular bone:
Axial compression	0.0029	0.0011	0.0018
Vertebra:
Axial compression	0.0002	0. 0001	0.0022
Anterior bending	0.0004	0.0	0.0007
Combined loading	0.0008	0. 0002	0.0048

Fig. 6.

Distribution of minimum principal strain for the columnar region of trabecular bone with the generic-anisotropic and specimen-specific, anisotropic material properties

Fig. 7.

(a) Direction of the primary Young's modulus and (b) Orientation of minimum principal strain in the midsagittal plane for a representative column model with generic-anisotropic and specimen-specific, anisotropic material properties. Each line represents the orientation for one element in the midsagittal plane.

3.1.3. Influence of DA.

The axial stiffness of the column increased with increasing DA (p < 0.001; Fig. 8(a)). Given that the morphology-elasticity constitutive model predicts an increase in elastic modulus along the primary material direction with increasing DA, the contribution of the primary elastic modulus to the axial stiffness of the column was identified by normalizing the axial stiffness with the average of the Young's moduli of the column in the superior-inferior direction (z-direction) (Fig. 8(b)). No difference (p = 0.181) was observed among the normalized axial stiffnesses for different values of DA.

Fig. 8.

Mean (n = 12) (a) axial stiffness of the column and (b) axial stiffness normalized with the average of the SI Young's modulus of the column of trabecular bone for varying DA. The axial stiffness of the column increased with increasing DA (p < 0.001). The error bars represent standard deviations.

3.2. FEA of Vertebra

3.2.1. Axial and Bending Stiffness.

No differences in either axial stiffness (p = 0.829) or bending stiffness (p = 0.359) were found between the FE models with the generic-anisotropic and the specimen-specific, anisotropic material properties (Table 1, Fig. 9). The axial stiffness (R ²= 0.82; p < 0.001) and bending stiffness (R²= 0.96; p < 0.001) for the two types of material properties were highly correlated.

Fig. 9.

(a) Axial stiffness (kN/mm) and (b) bending stiffness (MNmm/rad) obtained from finite element analyses using generic-anisotropic and specimen-specific, anisotropic material properties for 12 vertebrae. The dashed line represents 1:1 relationship.

3.2.2. Distribution and Directions of Minimum Principal Strain.

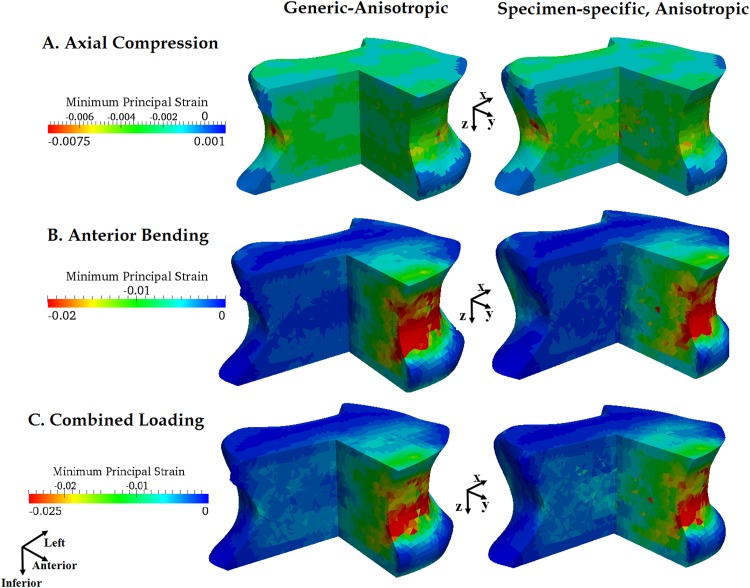
Only moderate variations in the distribution of minimum principal strains of the vertebra were observed within the vertebra between the generic-anisotropic and the specimen-specific, anisotropic material properties (Fig. 10). No differences in average strain were found between the two material properties for either loading mode (p > 0.278). When compared on an element-by-element basis, the magnitudes differed between different material properties (p < 0.001), but the magnitudes of the differences were small (Table 2). The directions of the minimum principal strains appeared to reflect the principal fabric directions and also the geometry of the vertebra (Fig. 11).

Fig. 10.

Distribution of minimum principal strain in one of the 12 vertebrae under axial compression, anterior bending, and combined loading obtained using the generic-anisotropy and specimen-specific, anisotropy based material properties

Fig. 11.

(a) Direction of the primary Young's modulus and (b) orientation of minimum principal strain (axial compression) at the midsagittal plane of one of the 12 vertebrae for generic-anisotropic and specimen-specific, anisotropic material properties. The lines are obtained for each element in the midsagittal plane of the vertebra.

3.2.3. Influence of DA.

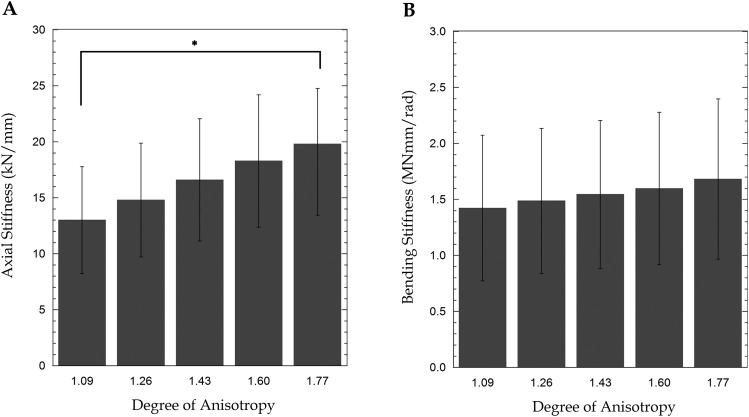
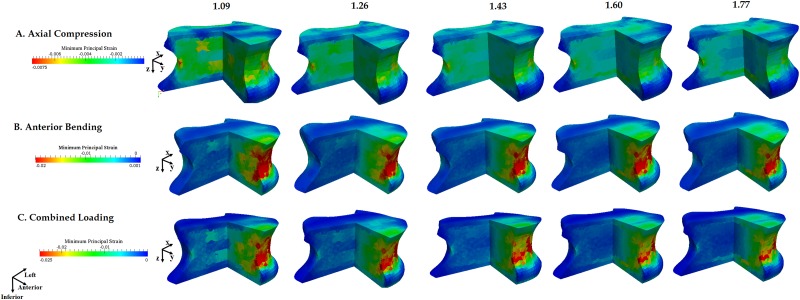
The axial stiffness of the vertebra increased with increasing DA (p = 0.007, Fig. 12(a)) whereas no effect of DA was observed for bending stiffness (p = 0.877, Fig. 12(b)). Only marginal changes in the strain distribution were observed for the bending and combined loading boundary conditions (Fig. 13). The magnitude of the maximum compressive strain (i.e., most compressive minimum principal strain) decreased with increasing DA (p = 0.008) for axial compression. The maximum compressive strain for DA = 1.77 was 37.43 ± 7.77% of the value predicted with DA = 1.09. However, for axial bending and combined loading, the maximum compressive strain did not differ among DA values (p > 0.056).

Fig. 12.

Mean (n = 12) (a) axial stiffness and (b) bending stiffness obtained from finite element analyses in which the degree of anisotropy (DA) was varied parametrically (* indicates a pairwise difference between the indicated groups (p < 0.05)). The error bars represent standard deviations.

Fig. 13.

Distribution of minimum principal strain under (a) axial compression, (b) anterior bending, and (c) combined loading in one of the 12 vertebrae modeled with different values of DA (shown above each column)

4. Discussion

In this study, we have investigated the effect of incorporating specimen-specific anisotropy and the influence of DA on the QCT-based FE predictions of vertebral stiffness and deformation patterns. The results from the FE analyses showed that incorporation of spatially varying trabecular anisotropy had a significant influence on the mechanical behavior of the central columnar region of the vertebra in isolation; however, when this columnar region was modeled within the entire vertebral body, the effects of the specimen-specific anisotropy were largely suppressed.

For the columns, the generic-anisotropic and specimen-specific, anisotropic material properties produced values of axial stiffness that were uncorrelated with one another (Fig. 5) and strain distributions that were different from one another (Fig. 6). Though the paired t-test indicated no differences in the stiffness values between the two types of material properties, these values were obtained using a tissue modulus of 13 GPa for the specimen-specific, anisotropic material properties. It is evident from literature that the tissue modulus can vary from 9.6 to 15.4 GPa [36,37]. If a lower tissue modulus were used, the axial stiffness of the column derived using the specimen-specific, anisotropic property would decrease.

Similar to the FE model of the column of trabecular bone, the stiffness of the vertebral body, whether under axial or flexural loading, was no different with the generic-anisotropic versus specimen-specific, anisotropic material properties (Fig. 9). However, unlike the results from the FE analyses of the column of trabecular bone, the FE predictions of the axial and bending stiffnesses of the vertebra were highly correlated between these two categories of material properties, and the predicted strain distributions were very similar to each other (Fig. 10). The above results, together with those from the column of trabecular bone, indicate that the regions of the vertebra not mapped by the μCT blocks (i.e., the cortical shell and peripheral regions of trabecular bone) contribute substantially to the mechanical behavior of the vertebra. This conclusion is consistent with experimental and numerical studies that indicate greater contributions to the mechanical integrity of vertebral bodies from the peripheral regions of the vertebra as compared to the trabecular core [38,39].

Numerous studies have shown the cortical shell alone to greatly influence the strength of vertebra [40,41]. The relative contribution of the load taken by the cortical shell varies with the axial distance from the endplates [42,43] and also increases with age [44]. A deterioration of the trabecular centrum also increases the relative load-bearing contribution of the cortical shell [3,45]. A recent study also found an interesting interaction of age and sex in the mechanical contribution of the peripheral regions, with these regions exhibiting an age-related increase in load-bearing in women but not in men [3]. These nuances in the load-carrying capacity of the shell and peripheral trabecular bone, together with the large contribution of the peripheral regions that we observed in this study, motivate further study of the role of specimen-specific anisotropy of the peripheral trabecular architecture in the mechanics of the entire vertebral body.

The combined role of the cortical shell and specimen-specific anisotropy in the vertebra was investigated recently using HR-pQCT FE models [20,21]. As compared to models with isotropic material properties, models with an explicit shell and with fabric-based, orthotropic material properties produced stiffnesses more closely matched to those computed from micro-finite element (μFE) models [21]. Incorporating fabric-based orthotropy in addition to an explicit shell also altered predictions of vertebral stiffness and strength as compared to models with no explicit shell and with fixed, transversely isotropic properties [20]. However, because no comparison between fabric-based material properties and generic-anisotropic material properties, where the FE models lack an explicit shell, was reported in these prior studies, we cannot make direct comparisons to our results. Even though the cortical shell was not explicitly modeled in our study, the material properties of periphery of the vertebra will have contributions from both the cortical shell and the adjoining peripheral trabecular tissue as the size of the QCT blocks (2.5 × 2.5 × 2.5 mm³) was larger than the average shell thickness of 0.35 mm [46]. Similarly, obtaining fabric measurements in the peripheral bone—a difficult task even with μCT due to the highly irregular architecture in and geometry of this region—will be an even greater challenge at clinical resolutions. The results of the present and prior studies suggest that accurate predictions of vertebral mechanical behavior from image-based FE models may require more information regarding vertebral microstructure than is presently obtainable in the clinical setting.

This study suffers from certain limitations. As noted earlier, the fabric information from the peripheral regions of the vertebra was not included in the FE models with the specimen-specific anisotropic material properties. The influence of specimen-specific anisotropy in these regions could be studied in the future using μFE models [8,47]. However, μFE models of the whole vertebra are computationally costly [48] and require higher-resolution images than are currently available clinically [49]. A second limitation is that, although the computed values of stiffness were very comparable to those measured experimentally by Kopperdahl et al. [50], the study design included no direct comparison to experiment. Nevertheless, the similarities shown in Figs. 9 and 10 suggest that, certainly in the absence of a method for specimen-specific modeling of the anisotropy of the peripheral regions, the generic-anisotropic material property is as good as the specimen-specific material property. A third limitation was the use of planar endplates to simplify the computational procedure and application of uniform boundary conditions. To understand the influence of the planar geometry, FE models were created without any cropping of the endplates for five of the 12 vertebrae used in this study. Elements were added adjacent to the endplate surfaces to simulate potting of the endplates in PMMA—a common procedure in ex vivo tests—and the compressive load was then applied to the vertebra via a rigid plate attached to the superior surface of PMMA. The stiffness values derived from cropped versus uncropped models were not different from one another (p = 0.184), and only moderate variations were observed in the distributions of the minimum principal strain. Also, a recent study on QCT-based FE models [51] showed excellent correlations for both ultimate force and damage distribution between cropped and uncropped (with PMMA) models. Even so, cropping of the endplates and applying uniform boundary conditions is likely a vast simplification of in vivo loading conditions. With degeneration of the intervertebral disks, the distribution of compressive load across the endplate shifts from a fairly uniform distribution [52,53] to one more heavily weighted on the regions underlying the outer annulus [54]. Increased load on the outer regions would be expected to change the load distribution between the peripheral and central regions of vertebra, further highlighting the need for accurate modeling of the peripheral region. A related limitation was exclusion of the posterior elements of the vertebrae. The results of this study may be most relevant for vertebrae adjacent to healthy disks because in this case the posterior elements carry only a small portion of the load in axial compression and anterior bending [55].

In summary, the results from this study indicate that the peripheral regions of the vertebral body can be highly influential in the mechanical behavior of this bone. As such, these results suggest two very different approaches to QCT-based FE modeling of vertebral bone, depending on the region to be modeled. For models of the trabecular centrum alone, the choice of anisotropic material properties can have substantial influence on the predictions of deformation and stiffness, and more realistic representations of the anisotropy can be advantageous. In contrast, for models of the entire vertebral body, and in the absence of specimen-specific data on the anisotropic mechanical behavior of the peripheral trabecular bone and shell, material properties corresponding to fixed, transverse isotropy suffice. Future studies are needed to develop approaches for using QCT images or other clinically obtainable data to model the specimen-specific, anisotropic mechanical behavior of the peripheral trabecular bone and shell. Further work is also needed to identify how the mechanical behavior of these peripheral regions varies with age, osteoporosis [11,15], and therapeutic interventions [56,57], all of which are known to alter the distribution of bone density and anisotropy throughout that vertebral body.