Table 2. Estimated marginal posterior mean for variance components and major gene parameters of ln(SI) using polygenic and mixed inheritance models in Bayesian segregation analysis¹.

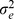
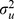
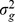
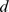
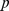
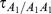
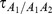
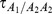
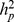
Model2											loge [p(y/Hi)] 3	Model tested	BF(H2; H1)4
1. General	0.011	0.110	3.408	1.36	−1.21	0.58	0.85	0.46	0.15	0.90	1,378.0	1 vs. 2	487.1
2. General fixed	0.087	[0]	35.834	5.72	−5.99	0.73	0.99	0.28	0.02	[0]	890.8	2 vs. 3	315.3
3. Sporadic	0.156	[0]	[0]	[0]	[0]	[0.0]	[0.0]	[0.0]	[0.0]	[0]	575.5	4 vs. 3	715.4
4. Polygenic	0.017	0.131	[0]	[0]	[0]	[0.0]	[0.0]	[0.0]	[0.0]	0.88	1,290.9	7 vs. 5	140.4
5. Dominant A2	0.015	0.121	0.055	0.23	0.23	0.45	[1.0]	[0.5]	[0.0]	0.89	1,354.3	5 vs. 1	−23.7
6. Additive	0.015	0.107	0.035	0.29	[0]	0.55	[1.0]	[0.5]	[0.0]	0.87	1,337.6	6 vs. 1	−40.4
7. Dominant A1	0.010	0.110	0.031	0.20	−0.20	0.52	[1.0]	[0.5]	[0.0]	0.91	1,494.7	7 vs. 1	116.8
8. Codominant	0.012	0.115	0.405	1.18	−0.13	0.46	[1.0]	[0.5]	[0.0]	0.90	1,343.2	8 vs. 1	−34.8

¹Bayesian segregation analysis of ln(SI) performed with software iBay version 1.46 [20]. The Gibbs sampler had these characteristics: number of iterations per chain = 1,200,000; burn-in period = 600,000; thinning = 10,000; collected samples per chain = 60; total chains = 20; and total collected samples = 1,200.

²Model parameters: error variance 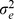; polygenic variance ; major gene variance 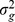; major gene additive effect ; major gene dominance effect 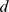; 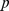is frequency of spleen size-decreasing allele A₁; 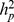is the polygenic model heritability 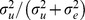; and transmission probabilities 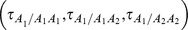defined as the probability that a parent with any of the three genotypes 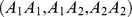transmits the allele 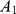to its offspring.

³ log _e of the marginal density under the fitted model H_i.

⁴Bayes factor BF(H₂; H₁) = p(y/H₂)/p(y/H₁) is the ratio of the marginal likelihood under one model to the marginal likelihood under a second model, and H₁ and H₂ are the two competing models.

⁵Value between squared brackets indicates the parameter was fixed to the value shown.