Automated and assisted RNA resonance assignment using NMR chemical shift statistics

Abstract

The three-dimensional structure determination of RNAs by NMR spectroscopy relies on chemical shift assignment, which still constitutes a bottleneck. In order to develop more efficient assignment strategies, we analysed relationships between sequence and ¹H and ¹³C chemical shifts. Statistics of resonances from regularly Watson–Crick base-paired RNA revealed highly characteristic chemical shift clusters. We developed two approaches using these statistics for chemical shift assignment of double-stranded RNA (dsRNA): a manual approach that yields starting points for resonance assignment and simplifies decision trees and an automated approach based on the recently introduced automated resonance assignment algorithm FLYA. Both strategies require only unlabeled RNAs and three 2D spectra for assigning the H2/C2, H5/C5, H6/C6, H8/C8 and H1′/C1′ chemical shifts. The manual approach proved to be efficient and robust when applied to the experimental data of RNAs with a size between 20 nt and 42 nt. The more advanced automated assignment approach was successfully applied to four stem-loop RNAs and a 42 nt siRNA, assigning 92–100% of the resonances from dsRNA regions correctly. This is the first automated approach for chemical shift assignment of non-exchangeable protons of RNA and their corresponding ¹³C resonances, which provides an important step toward automated structure determination of RNAs.

INTRODUCTION

Chemical shift assignment is a prerequisite for structure determination of biomolecules by NMR spectroscopy. Resonance assignment strategies for RNA are still mainly based on NOEs (1–4) because through-bond correlations are too insensitive (4) and can typically only complement but not replace the NOE-based approach (1). In contrast to proteins, for which ¹³C/¹⁵N labeling led to very robust assignment protocols, the small chemical shift dispersion of RNA signals hampers assignment strategies even if labeling is applied. Nevertheless, ¹³C/¹⁵N labeling helps to resolve some degeneracies and is crucial for the complete resonance assignment even for small RNAs. Due to the severe chemical shift overlap even in 3D spectra attempts to automate chemical shift assignments based solely on through-bond experiments seem to be out of reach.

A bottleneck of NOE-based sequential assignment strategies is to find good starting points, which are typically found by linking the more straightforward assignment of imino protons to non-exchangeable protons. However, typically only a small number of such anchor assignments can be obtained in this way and sometimes they are not unambiguous. A larger number of reliable anchor assignments would enhance resonance assignment strategies. In particular, the assignment of critical regions with chemical shift degeneracies that requires testing of several alternative assignment possibilities would benefit from additional reliable starting points. Our goal was to find characteristic RNA sequence-chemical shift relationships and to apply these for obtaining anchor assignments and global help for a reliable and efficient sequential RNA chemical shift assignment.

¹H chemical shifts of RNA and their dependence on the secondary structure and sequential neighbors were first systematically analysed in 2001 by the group of Wijmenga (5) using a small set of 28 RNAs. Based on this limited number of chemical shifts, it was found that H5, H6, H8 proton chemical shifts of dsRNA are predominantly influenced by the base type of the 5′-neighbor whereas the adenine H2 chemical shifts are influenced by both the 3′-neighbor and the 5′-neighbor. Recently, a more extensive analysis of ¹H chemical shifts and the influences of neighboring nucleotides was published (6). The authors assume that these influences are additive and provide an increment system to predict non-exchangeable ¹H chemical shifts for any base-paired triplet within a dsRNA. Investigations of ¹³C RNA chemical shifts have been sparse and mainly focused on the dependence of ribose resonances on the backbone conformation, the sugar pucker (7,8), and the secondary structure (9). Insufficient ¹³C data and inconsistent referencing hampered finding further structure-chemical shift relationships and in particular analysing the influence of neighboring residues on ¹³C chemical shifts. In another approach density functional theory (DFT) calculations were recently used to elucidate the relationship between ¹³C chemical shifts and the glycosidic torsion angle χ (10).

Whereas a large variety of automatic chemical shift assignment algorithms were developed for proteins (11,12), for example GARANT (13), AutoAssign (14), MARS (15), PINE (16) and FLYA (17), so far no comparably general, automated assignment approach was developed for RNA. The recently developed RNA-PAIRS algorithm (18) is able to automatically assign imino resonances of RNAs. It is very useful to derive and confirm the secondary structure of RNA but does not overcome the bottleneck of assigning the non-exchangeable protons that are essential for 3D structure determination. An automated resonance assignment program that assigns these non-exchangeable protons is therefore highly desirable.

Here we present ¹H and ¹³C chemical shift statistics for RNA that we used to develop efficient sequential assignment strategies for unlabeled RNA. We present manual assignment strategies based on the generation of starting points and the simplification of decision trees in the assignment walk. Finally, we present a fully automated assignment approach that consists of the new software Chess2FLYA and the FLYA algorithm (17) that was tested on several examples.

MATERIALS AND METHODS

Data mining

We collected all available RNA chemical shift entries of the BMRB database excluding RNA–protein and RNA–ligand complexes. An in-house C++ program was used to extract the BMRB number, the residue number and all available chemical shift values of every nucleotide that were further converted into a table (8). The secondary and tertiary structure information was extracted from PDB coordinates and publications. For each nucleotide i, the preceding i – 1 and succeeding i + 1 nt type was gathered, resulting in a triplet categorization like GAU. In addition, if present, Watson–Crick base-pairing of nucleotides i – 1, i and i + 1 was included. Terminal nucleotides were classified separately, as well as triplets containing a G•U wobble base pair. Chemical shift data of 15 additional RNAs reported only in publications were added manually. Details of all datasets used for the statistics and excluded chemical shift outliers are listed in Supplementary Table S1. ¹³C chemical shifts were validated and corrected as described (8).

1D statistics of ¹H and ¹³C chemical shifts

We focused our analysis on chemical shifts within regularly base-paired A-form RNA, in particular of the central nucleotides within a Watson–Crick base-paired triplet. In addition, we analysed chemical shifts of Watson–Crick base-pairs at the 5′ end and the 3′ end flanked by a Watson–Crick base-pair, and triplets containing a G•U wobble base pair. In this article, we use the following nomenclature for Watson–Crick base-paired nucleotides: XAY denotes an adenosine following a nucleotide of type X and preceding a nucleotide of type Y (always in the 5′ to 3′ direction). 5′GX denotes a Watson–Crick base-paired guanosine at the 5′ end. Nucleotides of G•U wobble base pairs are annotated with a superscript, e.g. CG^UX. 5′GGX denotes a guanosine within a Watson–Crick base-paired triplet next to the 5′ end starting with a guanosine. CC3′ denotes a cytidine at the 3′ end that follows a cytidine. Statistics are always given for the nuclei in the underlined nucleotide.

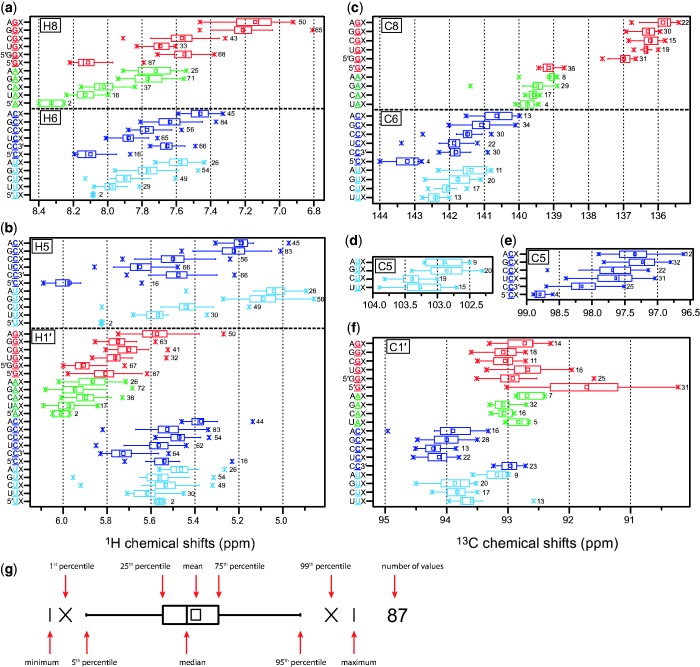
Chemical shift statistics of H2 and C2 were generated for each individual triplet category, for example the triplet GAU means an adenine succeeding a guanidine and preceding an uracil. Chemical shift statistics of H5, H6, H8, H1′, C5, C6, C8 and C1′ were generated for combined triplet categories in which the base type of nucleotide i + 1 is ignored, e.g. GAX, in which X can be any nucleotide. The same chemical shifts were also analysed for terminal nucleotides, e.g. for the categories 5′GX, CC3′ and 5′GGX. 1D statistical parameters for each chemical shift category were calculated using MicroCal OriginPro 8.5G (Microcal Software Inc.). The mean value, standard deviation, cluster size, skewness, minimum value, 25th percentile (1st quartile), median, 75th percentile (3rd quartile) and maximum value for each category are given in Supplementary Table S2. 1D statistical values are represented by box plots displaying the minimum, 5th percentile, 25th percentile, median, mean, 75th percentile, 95th percentile and maximum value (Figure 1).

Figure 1.

¹H and ¹³C chemical shift statistics for central nucleotides of Watson–Crick base-paired triplets in dependence of the RNA sequence displayed in form of box plots. Chemical shifts of residue i are given for a trinucleotide sequences consisting of residues i – 1, i and i + 1. Residue i is underlined. In addition, categories for nucleotides at the 5′ and 3′ terminus are displayed. The number of data points is given next to each box plot. (a) ¹H chemical shifts of H6 and H8. (b) ¹H chemical shifts of H5 and H1′. (c) ¹³C chemical shifts of base carbons C6 and C8. (d) ¹³C chemical shifts of C5 of uracils. (e) ¹³C chemical shifts of C5 of cytosines. (f) ¹³C chemical shifts of C1′. (g) Definition of the box plots.

2D statistical analysis of ¹H and ¹³C chemical shifts

For 2D statistical analysis an underlying bivariate normal distribution of the different clusters was assumed. The parameters of the distribution were estimated from the sample points as described by Batschelet (19). Bivariate normal distributions can be displayed by equidensity contours, also called covariance ellipses. We generated covariance ellipses that contain 86% of the sample values (19–21). The two semi-axes p₁, p₂ and the rotation angle α of the corresponding covariance ellipses were obtained as described by Paradowski (21). Covariance ellipses were then parameterized as described by Batschelet (19):

in order to display them directly in the NMR spectra analysis program SPARKY (22). The mean values µ₁, µ₂, standard deviations and the Pearson’s correlation coefficients for all C8–H8 and H5–H6 categories are given in Supplementary Tables S3 and S4, respectively. The ellipses that can be implemented in Sparky spectra are freely available under http://www.mol.biol.ethz.ch/groups/allain_group/members/schubert/software.

NMR spectroscopy

All NMR measurements were performed at 303 K on AVANCE (900 MHz) or AVANCE III (500, 600, 700 MHz) Bruker spectrometers equipped with cryogenetic triple-resonance probes. RNA samples in D₂O with typical concentrations of 1.5–2.5 mM were used. Natural abundance 2D ¹H–¹³C HSQC spectra were typically recorded with 220 transients. 2D ¹H–¹H NOESY spectra were measured with a mixing time of 250 ms and 48 scans. 2D ¹H–¹H TOCSY spectra were typically acquired using a mixing time of 50 ms and 4 scans. All spectra were referenced using an external sucrose/DSS sample (Bruker) as described previously (8). Data were processed with Topspin 2.1 (Bruker) and analysed with Sparky (22).

Preparing data for the FLYA automated resonance assignment algorithm

We developed the C++ program Chess2FLYA (Chemical shift statistics to FLYA) that uses RNA secondary structure information in the connectivity table format (.ct file format) and a built-in chemical shift statistics file to generate input files for the FLYA automated resonance assignment algorithm (17) implemented in the program package CYANA (12,23), namely a CYANA sequence file (.seq), an XEASY (24) chemical shift list (.prot) that incorporates the mean values and standard deviations from our 1D statistics, a torsion angle restraint file (.aco) that restricts the backbone of regular A-form RNA, and a file indicating the ranges of nucleotides involved in regular Watson–Crick base-pairs. Chess2FLYA is freely available under http://www.mol.biol.ethz.ch/groups/allain_group/members/schubert/software and http://www.bpc.uni-frankfurt.de/guentert/wiki/index.php/Chess2FLYA. The initial .ct files were created using RNAfold (25). The program Chess2FLYA determines chemical shift prediction intervals for each chemical shift taking into account also the samples sizes as described by Hahn and Meeker (26). For all calculations in this article the 60% prediction intervals were used. In a few cases for which an unusually narrow distribution was obtained due to a small number of values of related entries (sample standard deviation <0.1 ppm for ¹³C and <0.05 ppm for ¹H), the 60% prediction intervals were increased to a value typical for a distribution of the corresponding nucleus. The prediction intervals are used in FLYA as mean values and standard deviations for the building and scoring of assignments (see below). Chess2FLYA yielded generally narrow chemical shift prediction intervals for the nucleotides in dsRNA for which categorized chemical shift statistics were available. For other nucleotides that were not covered by the 1D chemical shift statistics of Figure 1 and Supplementary Figure S1 (i.e., any nucleotide not within a Watson–Crick base-paired triplet) the general BMRB statistics were used that comprise data from all secondary structures and do not consider the nucleotide type of the neighbors. These general BMRB statistics are therefore broad and unspecific.

For Watson–Crick base-pairs flanked on both sides by Watson–Crick base-pairs, torsion angles were restrained to values obtained from high-resolution crystal structures: α (−90° to −30°), β (150° to −150°), γ (30° to 90°), δ (50° to 110°), ε (180° to −120°) and ξ (−100° to −40°). For Watson–Crick base-pairs at the beginning of a regular double-stranded region, only the δ, ε and ξ angles were restrained. For Watson–Crick base-pairs at the end of a regular double-stranded region only the α, β, γ and δ angles were restrained. The file indicating the Watson–Crick base-pairs is used by CYANA to generate the corresponding hydrogen bond restraints.

Peak lists were prepared using the automatic peak-picking function in SPARKY and subsequently adjusted by visual inspection. Peaks were only picked in the chemical shift regions of the resonances of interest (excluding ribose resonances other than H1′ and C1′). The upfield limit for picking ¹H resonances was set based on the lowest H1′ or H5 chemical shift value in the ¹H–¹³C HSQC spectrum. In the TOCSY spectrum, peaks were only picked in the region of the uracil H5–H6 correlations. Peaks were picked on both sides of the diagonal in the TOCSY and NOESY spectra. Diagonal peaks were not picked.

Automated resonance assignment with the FLYA algorithm

Recently, we introduced the new FLYA automated resonance assignment algorithm for NMR spectra and showed that it is more general and yields more accurate results than other automated assignment methods for all chemical shifts in proteins (17). Here, we present its first application to nucleic acids. As primary input, the FLYA algorithm uses peak lists from multidimensional NMR spectra, e.g. for the calculations in this article 2D ¹H-¹H NOESY, 2D ¹H–¹H TOCSY and natural abundance ¹H–¹³C HSQC. Instead of prescribing a specific assignment strategy, the algorithm generates the peaks expected in each given spectrum by applying a set of rules for through-bond or through-space magnetization transfer, and determines the resonance assignment by constructing an optimal mapping between the expected peaks, assigned by definition but having unknown positions, and the measured peaks, initially unassigned but with known positions in the spectrum (13,17,27,28). An evolutionary algorithm combined with local optimization is used to maximize a scoring function that takes into account the distribution of chemical shift values with respect to general shift statistics, the alignment of peaks assigned to the same atom, the completeness of the assignment, and a penalty for chemical shift degeneracy. All experimental data is used simultaneously in order to exploit optimally the redundancy present in the input peak lists. The scoring and optimization of RNA assignments were performed in FLYA as described for protein NMR data (17).

FLYA reports a chemical shift for each nucleus that is assigned to at least one peak. Here, we restricted the generation of expected peaks to the most dispersed signals, namely H2, H5, H6, H8, H1′, and their corresponding carbon resonances, i.e. FLYA did not attempt to assign other nuclei. Expected TOCSY peaks were generated for the pyrimidine intra-base H5–H6 correlations. Expected ¹H–¹³C HSQC peaks were generated for the one-bond H2–C2, H5–C5, H6–C6, H8–C8 and H1′–C1′ correlations. NOESY peaks are expected to be observed for intra-nucleotide correlations, correlations between sequentially neighboring nucleotides, and correlations between based-paired nucleotides. To obtain the respective atom pairs, the FLYA algorithm generates an ensemble of structures of the respective RNAs that fulfill the hydrogen bond restraints for the Watson–Crick pairs and the angle restraints but are otherwise random. These random structures were generated by the CYANA torsion angle dynamics algorithm (23) using the standard simulated annealing protocol with 10 000 torsion angle dynamics steps per structure. Calculations were started from 500 random initial conformers with random torsion angle values. After simulated annealing the 20 structures with lowest CYANA target function value were retained for analysis. No assumption on the tertiary structure of the RNAs is made. Hence, these random structures sample a bigger conformational space than the correct structure, which leads to a wider range of observed distances between two specific atoms. To guarantee that all relevant correlations are considered, expected NOESY peaks were generated for H–H distances up to 14 Å in all random structures. This high distance limit takes into account the maximal distance for a detectable NOE of about 6 Å, and the possible deviations of the random structures from the unknown correct structure. Expected peak probabilities were set to 0.9, 0.8 0.5 and 0.3, respectively, for distances that were shorter than 4, 6, 9 and 14 Å in all random structures simultaneously.

The tolerance for the chemical shift matching in the FLYA algorithm was 0.02 ppm for ¹H and 0.3 ppm for ¹³C. The population size in the evolutionary algorithm was 100. Chemical shift assignments were consolidated from 20 independent runs with different random number seeds. The assignment of an atom was classified as ‘strong’ if at least 80% of the 20 chemical shift values from these runs differed less than the matching tolerance from the consensus value.

RESULTS

Database composition

The amount of RNA chemical shift data increased significantly since their first statistical analysis by the group of Wijmenga (5) 12 years ago, prompting us to search for new sequence-chemical shift relationships, in particular on the influence of sequential neighbors on certain nucleotide chemical shifts in a regular A-form dsRNA structure. Making use of our corrected lists of ¹³C RNA chemical shifts (8), we compiled a large and reliable ¹H and ¹³C chemical shift database by extracting ¹H and ¹³C chemical shifts from 114 RNA datasets originating from the BMRB database (29) and from publications. Since perturbations from regular chemical shifts are expected for protein–RNA complexes and RNA–ligand complexes, we excluded such datasets. Parts of RNAs containing tertiary structure such as pseudoknots were also excluded. We focused our statistical analysis on ¹H and ¹³C chemical shifts of regular A-form RNA, i.e. Watson–Crick base-paired nucleotides flanked by Watson–Crick base-pairs on either side. This results in 64 possible nucleotide triplets in a dsRNA. In addition, we analysed the chemical shifts of closing base-pairs at the 3′ and 5′ end of dsRNA.

RNA chemical shift statistics

1D chemical shift statistics

We analysed ¹H chemical shifts of H2, H5, H6, H8, H1′ and the corresponding ¹³C chemical shifts of C2, C5, C6, C8, C1′ for the central nucleotide of each possible Watson–Crick base-paired triplet. The 1D statistics are presented in the form of box plots (Figure 1 and Supplementary Figure S1). This representation provides a quick overview of the data without making assumptions on the underlying statistical distribution. The spacing between different parts of the box helps to indicate the degree of dispersion and skewness of the data and to identify outliers. We made statistics for the central nucleotide of three consecutive Watson–Crick pairs. Since the base proton chemical shifts of H5, H6 and H8 are mainly influenced by the 5′-neighbor (5,6) but only slightly by the 3′-neighbor (6) (Supplementary Figure S2), we combined the Watson–Crick base-paired triplets into 16 categories based on the initial dinucleotide sequence, for example AGX. Additional categories were introduced for closing base-pairs at the 3′ and 5′ termini of regular dsRNA: 5′AX, 5′CX, 5′GX, 5′UX and CC3′. H2 resonances are influenced by both, the 3′ and the 5′ neighboring base type, and categories of trinucleotide sequences (XAY) were analysed as shown in Supplementary Figure S1a. The nucleotide type preceding the Watson–Crick base-paired triplets did not have a significant influence on the chemical shifts. However, if the first nucleotide of the Watson–Crick base-paired triplet was the 5′ terminus, a significant influence was observed. We therefore introduced the additional category 5′GGX. For other triplets at the 5′ terminus there were not enough values for a statistical analysis. In addition, we analysed the influence of G•U wobble base pairs on chemical shifts. The ¹H chemical shifts of both nucleotides of a G•U wobble base pair (XG^UY and XU^GY) are similar to those of Watson–Crick paired XGY and XUY triplets (Supplementary Figure S3a and b) except that the H5 chemical shifts of U^G are significantly downfield shifted (∼0.3 ppm), and some H8, H6 and H1′ resonance distributions show smaller deviations (<0.15 ppm). The influence of a 5′ neighboring G•U wobble base pair on the H1′ chemical shifts was similar to G or U 5′ neighbor within a Watson–Crick base pair except purine H8 resonances are less upfield shifted (∼0.2 ppm) when U^G is the 5′ neighbor and pyrimidine H5 resonances are less upfield shifted (∼0.1 ppm) when G^U is the 5′ neighbor (Supplementary Figure S3c and d).

All H6 and H8 (Figure 1a) and also H5 and H1′ (Figure 1b) chemical shifts show dependencies on the base type of the 5′-neighbor and H2 chemical shifts (Supplementary Figure S1a) on the base types of both sequential neighbors as reported earlier (5,6). For example the cytidine H6 chemical shifts range from 7.3 ppm to 8.2 ppm, displaying the lowest values if the preceding base is an A (∼7.46 ppm). If the preceding nucleotide is a G, the values increase to ∼7.64 ppm, in case of a C to ∼7.77 ppm and of U to ∼7.88 ppm. This is a trend that is observed for most proton chemical shifts, namely H6, H8, H5 and H1′. A distinct higher chemical shift is found for protons of a nucleotide at the 5′ end. Although only few H2 data were available for some triplet categories they display clearly different chemical shift regions. The most separate H2 chemical shift is that of UAA at 6.46 ± 0.06 ppm which does not overlap with any other chemical shifts. This was used previously as a diagnostic tool to detect base-pairing in an RNA as large as 356 nt (30).

We provide statistical values for each analysed distribution (Supplementary Table S2). These statistics are complementary to the approach of Barton et al. (6) whose goal was to predict ¹H chemical shifts based on tabulated contributions of the neighborhood assuming that those contributions are additive. In contrast, we analysed the actually observed chemical shift ranges and derived statistical values. Furthermore, we analysed for the first time trends of ¹³C resonances in dsRNA. The resulting chemical shift statistics are provided for the ¹³C resonances of C6 and C8 (Figure 1c), C5 (Figure 1d and e), C1′ (Figure 1f) and C2 (Supplementary Figure S1b). Very clear and narrow clusters were obtained. For many ¹³C chemical shifts a dependency on the 5′-neighbor was observed as well. For example, cytosine C6 chemical shifts follow the same trend as H6 chemical shifts in regard to the preceding base: increasing values in the order of A, G, C and U. Clearly distinct ¹³C chemical shifts were obtained for nucleotides at the 5′ end and for C1′ of a cytidine at the 3′ end.

2D chemical shift statistics

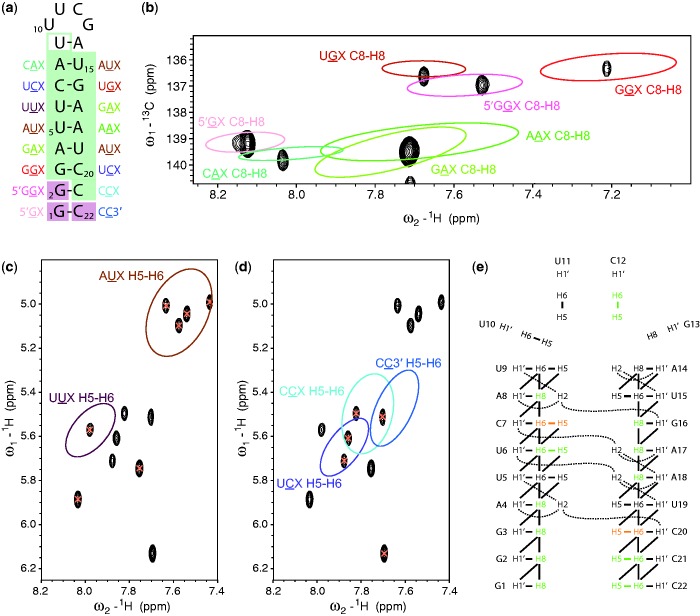
Spreading out the chemical shift data into two dimensions results in an even better separation of the different categories. Scatter plots of chemical shift pairs were generated for different triplet categories. We assumed that the different clusters have an underlying bivariate normal distribution and represented the distributions by covariance ellipses at a contour of 86% probability. Separated clusters were observed for H5–H6 correlations found in 2D TOCSY spectra (Figure 2a) and C8–H8 correlation found in ¹H–¹³C HSQC spectra (Figure 2b). The pyrimidine H5–H6 correlations show a large dispersion and despite some overlap between ellipses, many clusters are clearly separated, e.g. UUX from GUX. The C8 resonances of guanines are clearly separated from those of adenines. An exception is the cluster of 5′ terminal guanines (5′GX) that borders two adenosine clusters (UAX, CAX). However, the 5′GX cluster can be clearly distinguished from the GAX and AAX clusters. The ellipses of C8–H8 correlations of guanosines following a purine (AGX and GGX) are clearly separated from those that follow a pyrimidine (CGX, UGX). In addition, 2D statistics of H6/H8–H1′ correlations (resonances within the same nucleotide) were analysed (Supplementary Figure S4) resulting in similarly well-separated clusters.

Figure 2.

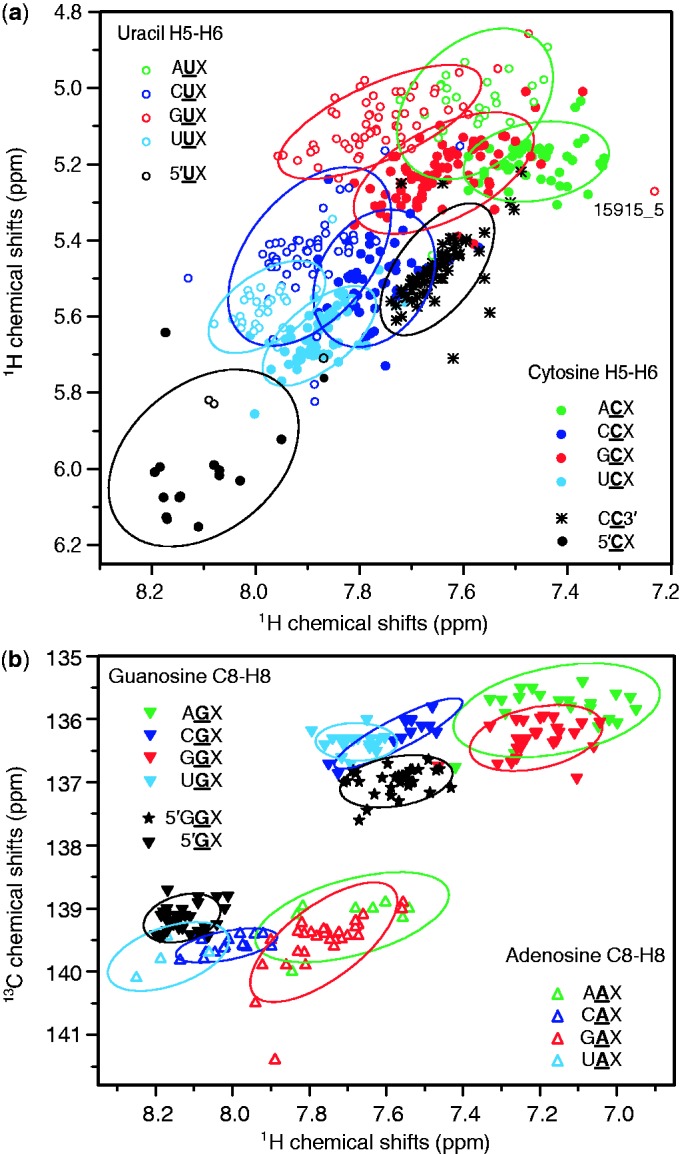
Two-dimensional chemical shift statistics for the central nucleotide of Watson–Crick base-paired triplets. Scatter plots display the clusters of chemical shift correlations for the different categories. Bivariate normal distributions are represented by ellipses at 86% probability. (a) H5–H6 chemical shift correlations that are found in a 2D ¹H–¹H TOCSY spectrum. (b) C8–H8 chemical shift correlations that are found in a 2D ¹H–¹³C HSQC spectrum.

Use of chemical shift statistics for efficient manual assignment of dsRNA

Based on our chemical shift statistics we developed an efficient resonance assignment strategy for the most dispersed non-exchangeable protons (namely H2, H5, H6, H8, H1′) and their corresponding ¹³C nuclei that is applicable to dsRNA with ¹³C at natural abundance. The method requires the acquisition of only three 2D NMR spectra: 2D NOESY, 2D TOCSY and a 2D natural abundance ¹H-¹³C HSQC (all measured in D₂O for a total recording time of about 48 h). To use the chemical shift statistics in an efficient manner, we provide covariance ellipses that can be directly displayed in the NMR assignment software Sparky (22). The 2D chemical shift statistics yielded a redundant amount of starting points for the assignment as illustrated in the following. This approach is more direct than the conventional strategy in which the assignment of the non-exchangeable protons depends on an initial assignment of the imino protons in the 2D NOESY spectrum in H₂O followed by a subsequent assignment of adenine H2 resonances of A-U base-pairs. Our new strategy was applied to assign the six RNA stem-loops FZL2, FZL4, RP1, TASL1, TASL2, TASL3 with 21–30 nt that were introduced in a previous publication (8) and a small interfering RNA (siRNA) of 42 nt (Supplementary Figure S5).

Finding starting points for sequential resonance assignment using 2D TOCSY and ¹H-¹³C HSQC spectra

We illustrate the strategy using the 22 nt RNA stem-loop TASL1 as an example (Figure 3a). Triplet-based chemical shift statistics are available for nucleotides 1–8 and 15–22, representing an A-form RNA environment and the most common terminal nucleotides. From the secondary structure it is apparent that only a subset of the existing Watson–Crick base-paired triplets is present in TASL1 (indicated next to every nucleotide in Figure 3a). Covariance ellipses of the categories found in TASL1 were superimposed on the corresponding 2D NMR spectra using the program Sparky (Figure 3b–d). Figure 3b shows the C8–H8 region of the ¹H–¹³C HSQC spectrum with superimposed covariance ellipses belonging to the C8–H8 categories for the triplets 5′GX, 5′GGX, GGX, UGX, AAX, CAX and GAX (found twice in the RNA sequence). In the ellipse of the category 5′GX there is only one cross-peak, suggesting that it can be assigned to G1. The cross-peak in the ellipse of the category 5′GGX suggests to originate from G2. This way all purine C8–H8 correlations of the stem can be assigned in TASL1. The strong signal within the ellipses of AAX and GAX suggests to contain the three expected cross-peaks of A4, A17 and A18. Assignments for G1, G2, G3, A4, A8, G16, A17 and A18 can be made immediately since only one signal per ellipse is observed. All those eight assignments were correct when compared to the consolidated resonance data.

Figure 3.

Application of 2D chemical shift statistics for proposing starting points for the assignment of the 22 nt RNA TASL1. (a) Secondary structure of TASL1. The region of regular dsRNA for which the statistics were made is highlighted in green. The chemical shifts of the last nucleotide of the stem (closing base-pair before the loop) typically fall within the clusters of regular dsRNA and thus the nucleotide is boxed in green (unfilled). In addition, the terminal nucleotides for which separate statistics were generated are boxed in pink. (b) Region of the ¹H–¹³C HSQC of TASL1 showing C8–H8 correlations. The corresponding bivariate normal distributions are displayed in form of ellipses. (c) H5–H6 correlations in a 2D TOCSY spectrum of TASL1 with uracil signals highlighted by orange crosses. (d) H5–H6 correlations in a 2D TOCSY spectrum of TASL1 with cytosine signals highlighted by orange crosses. Only one cytosine cross-peak is located outside the ellipses, which originates from the cytosine in the loop. (e) Scheme of the expected NOE correlations between aromatic and H1′ protons. The 12 unambiguous starting points for resonance assignment obtained from 2D H5–H6 and H8–C8 chemical shift statistics are indicated in green. Ambiguous predictions are shown in orange.

Whereas the ¹H–¹³C HSQC spectrum yielded valuable starting assignments of purines, the 12 H5–H6 cross-peaks observed in the TOCSY spectrum of TASL1 (Figure 3c and d) originate from five cytosines and seven uracils. We expect H5–H6 peaks from pyrimidines of the stem that belong to the following five categories AUX (4×), CCX, UCX (twice), UUX and CC3′ whose covariance ellipses are shown in Figure 3. For the pyrimidine resonances in the loop (U9, U10, U11 and C12), only general statistics are available (not shown). The H5 resonances of cytosines and uracils were distinguished by their ¹³C chemical shift. Uracil H5–H6 signals are highlighted in Figure 3c with the corresponding covariance ellipses for AUX and UUX. Only one cross-peak can be found in the ellipse representing the cluster of UUX so that this signal can be assigned to U6. Three signals within the ellipse of the AUX cluster are expected for nucleotides U5, U15 and U19 but four signals are observed (the closing base-pair U9 falls in the same region). The two uracil signals located outside the marked ellipses correspond to nucleotides of the loop. Figure 3d shows a similar overlay for the cytosines. The ellipse for CC3′ contains only one signal, which could be assigned to C22. Two signals are expected within the UCX ellipse (from C7 and C20) and one within the CCX ellipse (from C21). Although the ellipses overlap and some signals are part of two ellipses our statistical approach would suggest that C7 and C20 can be assigned to the two signals within the UCX ellipse (still ambiguous), C22 to the single signal within the CC3′ ellipse and C21 to the signal within the CCX ellipse that does not overlap with other ellipses. The remaining cytosine cross-peak with the most downfield H6 resonance, far away from the indicated ellipses, originates from C12 in the loop. This illustrates how many unambiguous and ambiguous assignments can be made immediately with this approach. These assignments can be used as starting points for the full resonance assignment. With only two spectra, a 2D TOCSY and a natural abundance ¹H-¹³C HSQC, we could determine immediately 12 unambiguous resonance assignments for 12 different nucleotides in this 22 nt RNA stem-loop that can be used as starting points for the full resonance assignment. All of those 12 assignments were correct. For regular dsRNA typical NOE signals are expected as illustrated schematically in Figure 3e. The 12 unambiguous and the 2 ambiguous starting assignments for the 22 nt TASL1 are nicely distributed over the entire RNA structure and are next used to find expected NOE patterns. By analysing these patterns in the 2D NOESY spectrum the starting points could be verified, ambiguous starting points unambiguously assigned, and the gaps in the assignment filled within a few hours of manual analysis. As an example, Supplementary Figure S6 illustrates how the H6/H8 starting points can be linked by a H6/H8–H6/H8 sequential walk. With increasing size of the RNA more correlations of the same triplet category are expected leading to several cross-peaks within the same ellipse as illustrated with the 42 nt siRNA (Supplementary Figure S5). However, some unambiguous and a variety of ambiguous assignment suggestions are good starting points for resonance assignment.

Application of the statistics for further assignments

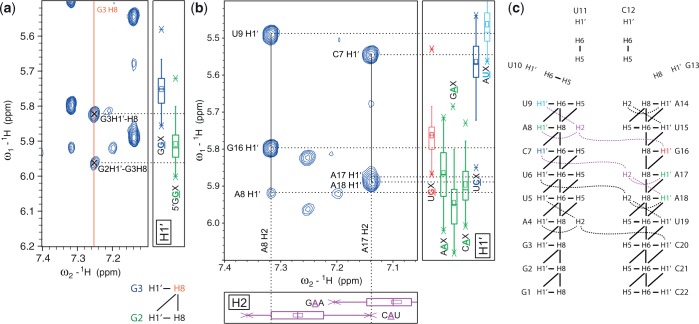
The chemical shift statistics are not only helpful to obtain rapidly initial resonance assignments, but also in all subsequent assignment steps as the statistics restrict the region where a cross-peak is expected and thereby reduce significantly the number of assignment possibilities. The following example uses 1D statistics during the H1′–H6/H8 sequential assignment walk in a 2D NOESY spectrum. In an A-form RNA helix, a purine H8 resonance has two correlations of medium intensity to its own H1′ and the H1′ of the preceding residue. Starting with an already assigned H8 resonance that displays two H1′ correlations, the 1D statistics for H1′ can then unambiguously distinguish these two H1′ chemical shifts and assign them to either intra-nucleotide or inter-nucleotide correlations (Figure 4).

Figure 4.

Application of 1D statistics during assignment walks. (a) Part of a 2D NOESY spectrum of TASL1 showing cross-peaks of the G3 H8 resonance that was already assigned based on 2D statistics. As illustrated schematically (bottom) the expected NOE correlations include two cross-peaks to H1′ resonances, one to nucleotide G2 and one to G3. The 1D statistics (right) help here to differentiate between the two cross-peaks assigning them to G2 H1′–G3 H8 and G3 H1′–H8. Only one of the ¹H chemical shifts lies within the borders of the GGX statistic and is therefore assigned to G3 H1′. The other ¹H chemical shift lies within the borders of the 5′GGX statistic and is assigned to G2 H1′. (b) Cross-peaks of two adenosine H2 resonances in the 2D NOESY spectrum of TASL1. At the bottom and on the right 1D statistics of the relevant triplets are displayed. (c) Scheme of TASL1 showing expected NOE correlations. The two adenosine H2 resonances and their correlations visible in the NOESY spectrum are colored in magenta. The involved H1′ resonances are color-coded as the chemical shifts statistics in panel b.

Chemical shift statistics are also useful during the assignment of NOE cross-peaks between H1′ and adenosine H2 resonances as illustrated in Figure 4b and c. The RNA TASL1 contains five adenosines whose H2 resonances were readily identified based on their signals in a ¹H–¹³C HSQC spectrum displaying the characteristic C2 chemical shift between 150 ppm and 155 ppm. Figure 4b shows the NOE patterns of two H2 resonances. Of the five adenosines and their corresponding H2 chemical shift statistics (Supplementary Figure S1) two box plots (CAU and GAA) show chemical shifts between 7.1 ppm and 7.3 ppm. The H1′ chemical shift statistics of expected NOE correlations with the involved adenosines A8 and A17 (indicated in magenta in Figure 4c) are displayed next to the spectrum (Figure 4b). The statistics can be used either as a confirmation during the assignment walk or to obtain starting points. For instance, the strong cross-strand NOE of A17 H2 to C7 H1′ can be readily assigned based on the box plots (H2 GAA and H1′ UCX) as shown in Figure 4b.

Another robust approach to enter the H1′–H6/H8 sequential assignment walk is based on H5–H8 correlations between a pyrimidine that follows a purine using a combination of 2D and 1D statistics. The approach is illustrated for the 30 nt RNA TASL3 in Supplementary Figure S7 that shows the characteristic NOE pattern in panels a and b. The H5–H6 correlations within the covariance ellipses of AUX and GCX serve as ambiguous starting points. For example, the signals 5 and 6 in the 2D TOCSY spectrum can be assigned ambiguously to C11 and C21. The same H5–H6 correlations are strongly present in the 2D NOESY spectrum. In addition, weak H5–H8_{i – 1} signals (red arrows) are clearly visible in this well-dispersed region of the 2D NOESY spectrum. These signals linked to H5–H6 starting point correlations, e.g. of pyrimidine i, provide the H8 chemical shift of the previous purine (i – 1). The H8 chemical shifts in turn reflect the influence of the predecessor of the purine (residue i – 2, see panels a and b). Applying the 1D statistics of purine H8 chemical shifts within triplets that occur in the sequence (panel f) removes some ambiguities. For instance, the cytosine signals 5 and 6 can now be distinguished: signal 5 originates likely from an AGCX quartet and signal 6 from an UGCX quartet resulting in the unambiguous assignment to C21 and C11, respectively. In a similar way, signals 1 and 4 can be assigned to U5 and U27 (still ambiguous), whereas signals 2 and 3 can be assigned to U9 and U23 (still ambiguous).

Fully automated RNA assignment of unlabeled RNA

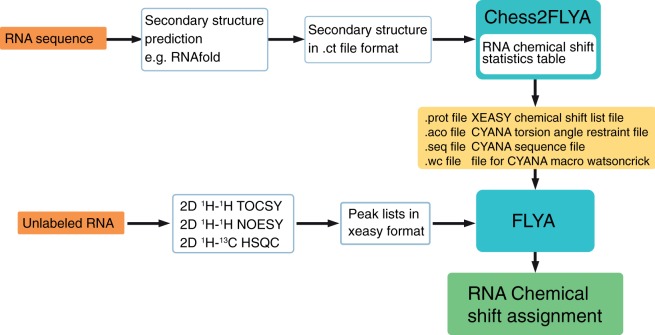
Based on the automated NMR assignment algorithm FLYA, we developed a strategy for automatically assigning RNA resonances of dsRNA using our 1D chemical shift statistics. FLYA was initially developed for protein assignment but is generally applicable (17). The workflow is illustrated in Figure 5. In the first step the program Chess2FLYA combines RNA secondary structure information with chemical shift statistics to create input files for FLYA. Beside the RNA secondary structure, NMR peak lists of three 2D spectra are required. The peak lists can be picked automatically, but a visual inspection and correction improves the performance. Using the chemical shift statistics, peak lists and information about hydrogen bonds and backbone-angle restraints FLYA generates a chemical shift assignment of the atoms. In order to give information about the reliability of the results, FLYA classifies the assignments into ‘strong’ and ‘weak’. ‘Strong’ means that an assignment is consistent within at least 80% of 20 independent runs of the algorithm and is therefore considered to be more reliable than others.

Figure 5.

Workflow of automated RNA assignment with the programs Chess2FLYA and FLYA. RNA secondary structure information in the connectivity table format (.ct file format) is used as an input for the program Chess2FLYA. RNA chemical shift statistics are supplied with the program, which generates .prot, .aco, .seq and .wc input files that are then used as an input of the FLYA automated resonance assignment algorithm (17). In addition, FLYA is supplied with peak lists of a 2D TOCSY, a 2D NOESY and a natural abundance ¹H–¹³C HSQC spectrum in order to obtain the RNA assignment.

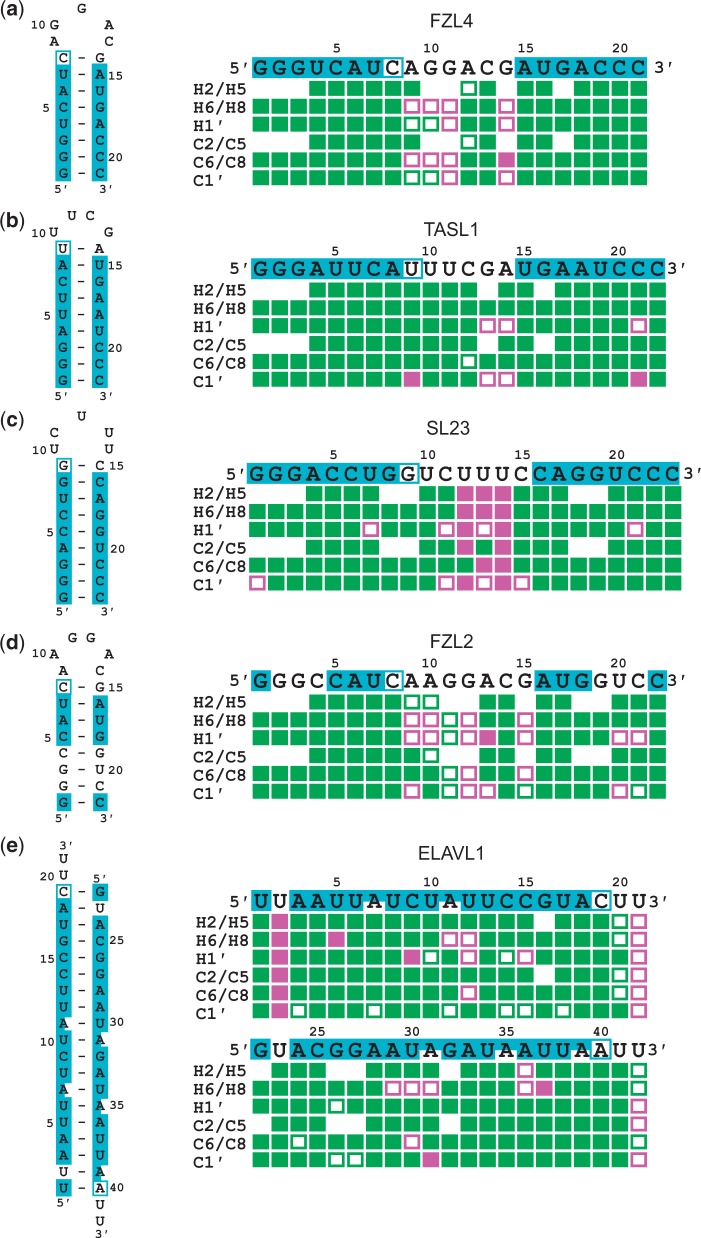
We applied this automated assignment procedure to four RNA stem-loops and a 42 nt siRNA (Figure 6). One of the stem-loops contains a G•U wobble base pair. Statistics of the input peak lists are given in Supplementary Table S5. The following analysis focuses on the results for H2, H5, H6, H8, H1′, and their corresponding carbon resonances that are based on categorized 1D chemical shift statistics of Watson–Crick base-paired triplets (Figure 1 and Supplementary Figure S1). The correctness of the automated assignments is illustrated in Figure 6 and Table 1, and the individual assignments are listed in Supplementary Tables S6–S10. In the regular dsRNA regions of the stem-loops (Figure 6 a–d), on average 99% of the aforementioned resonances were correctly assigned. Except for one ¹³C chemical shift (C1′ of C21 in TASL1) all assignments with strong support within regular double-stranded regions were correct. This incorrect ¹³C assignment was caused by severely overlapping cross-peaks in the ¹H–¹³C HSQC spectrum resulting in an incomplete input peak list. Although peaks on ‘shoulders’ were added and peak positions adjusted for such regions during manual inspection of the automatically picked peaks, some overlapped signals could not be picked. Since the input data contained only a single peak list with ¹³C chemical shifts, i.e. there could be at most one peak for every ¹³C nucleus, an unambiguous ¹³C assignment is not possible in these cases. Considering the degeneracies in the spectra of these example stem-loop RNAs, the correctness of the assignments for the dsRNA regions is remarkable. Even in the case of the G•U wobble base pair-containing stem-loop (Figure 6d) only three incorrect assignments occurred within this stem, all with weak support. On the other hand, assignments in loop and other unclassified regions were much less reliable, ranging from 53% to 85% correctness. This had to be expected because only general chemical shift statistics from the BMRB database were available for these regions. The FLYA results for the loop regions are still useful, since they provide tentative assignments that can be verified manually.

Figure 6.

Assignment of five RNAs by the fully automated assignment approach using Chess2FLYA and FLYA. Regions with triplet-based statistics (central nucleotide of a Watson–Crick base-paired triplet) and of Watson–Crick base-paired termini are colored in cyan. Nucleotides before irregularities with statistics that only consider the base type are shown in cyan boxes. For unmarked nucleotides only general statistics were available. This is the case for nucleotides without Watson–Crick base-pairing in loops. Adenosines with a smaller cyan box lacked ¹³C statistics of C2 due to insufficient chemical shift data. The results of the automated chemical shift assignment by FLYA are color-coded: green and magenta boxes indicate correct and incorrect assignments, respectively. Full boxes correspond to strong (self-consistent) FLYA assignments, empty boxes to weak (tentative) assignments.

Table 1.

Percentages of correct/incorrect assignments by the fully automated assignment approach using Chess2FLYA and FLYA^a

	FZL4 (%)	TASL1 (%)	SL23 (%)	FZL2 (%)	ELAVL1 (%)
dsRNA (categorized statistics available):
Correct (total)	100.0	97.7	96.4	100.0	92.1
Strong	100.0	97.7	96.4	100.0	85.7
Weak	0.0	0.0	0.0	0.0	6.3
Incorrect (total)	0.0	2.3	3.6	0.0	7.9
Strong	0.0	1.1	0.0	0.0	2.1
Weak	0.0	1.1	3.6	0.0	5.8
Correctness of strong assignments	100.0	98.9	100.0	100.0	97.6
Loop regions, bulges etc. (only general statistics available):
Correct (total)	66.7	85.3	52.5	76.4	71.7
Strong	50.5	82.4	52.5	63.9	58.5
Weak	16.7	2.9	0.0	12.5	13.2
Incorrect (total)	33.3	14.7	47.5	23.6	28.3
Strong	2.7	2.9	35.0	1.4	11.3
Weak	30.6	11.8	12.5	22.2	17.0
Correctness of strong assignments	94.7	96.6	60.0	97.9	83.8

^aAssignments were compared to the manually determined reference assignments and classified as correct if they agreed with the reference assignment within the matching tolerance of 0.02 ppm for ¹H and 0.3 ppm for ¹³C. The class ‘dsRNA’ corresponds to the residues marked by filled cyan boxes in Figure 6, the class ‘Loop regions, bulges etc.’ to all other residues. The entries in the table correspond to the color code for resonance assignments in Figure 6 as follows: correct, strong (filled green boxes in Figure 6); correct, weak (open green boxes); incorrect, strong (filled magenta boxes); incorrect, weak (open magenta boxes). The assignment of an atom was classified as ‘strong’ if at least 80% of its chemical shift values from 20 independent runs of the FLYA algorithm differed less than the matching tolerance from the consensus value.

The ELAVL1 siRNA with 42 nt challenges the FLYA algorithm especially because of its size and similar segments occur twice (AAUUA). FLYA could assign 92% of the resonances in the double-stranded region (cyan in Figure 6 and Supplementary Table S10) correctly, and 98% of the assignments with strong support within the double-stranded regions were correct. Compared to the stem-loop RNAs, there are more assignments with weak support (open rectangles) of which ∼50% were correct. Overall, the program FLYA performed remarkably well in assigning the ELAVL1 siRNA despite of its large size and partially repetitive sequence.

DISCUSSION

The chemical shift statistics presented in this article enabled us to develop assisted and fully automated methods for RNA assignment. The resonance assignment was restricted to the most disperse resonances H2, H5, H6, H8, H1′, and their corresponding ¹³C chemical shifts—that is approximately equivalent to the backbone assignment of proteins.

The manual assignment of all these resonances could be accomplished within 1 or 2 days for each of the six RNA stem-loops with 20–30 nt tested, except for a few carbon resonances that could not be assigned unambiguously due to degeneracies in the ¹H–¹³C HSQC spectrum. We were able to assign a siRNA of 42 nt with the manual strategy. The size limit of the RNAs to which our method can be applied is ∼40 nt depending on the sequence. Limitations of our strategy are expected for repetitive sequences, e.g. AUAUAU or CAUCAUCAU, for which many resonances will coincide. The statistics provided a redundant amount of starting points that simplified the assignment process drastically. Most immediate assignments were obtained with the ¹H–¹³C HSQC spectrum, emphasizing the importance of ¹³C chemical shifts and their combination with proton resonances. The statistics proved to be reliable: in all cases the ellipses of the bivariate distributions covered the area in which the finally assigned cross-peak was found. Traditional strategies to enter the NOESY assignment walks of the non-exchangeable protons using H2 could be used in addition. 1D statistics for H2 (Supplementary Figure S1) can be used to confirm these conventional starting points. 1D statistics helped to increase the speed and completeness of the dsRNA assignment, which, in turn, was of advantage to assign the remaining bulge and loop regions. Resonances outside the dsRNA bivariate distributions typically originated from loop regions or mismatches.

Combining the chemical shift statistics with the FLYA algorithm enabled for the first time the reliable automated assignment of the H2, H5, H6, H8, H1′, and corresponding ¹³C resonances in dsRNA. This extends the realm of automated resonance assignment from proteins to nucleic acids and strongly reduces the human time effort needed for assigning dsRNA, even when a manual verification is included as a safeguard against the small number of incorrect assignments within dsRNA. The automated approach also yields assignments in the loops and other regions of non-regular secondary structure. However, these are tentative and manual methods are required for reliably assigning these regions.

Both assignment methods presented in this article are fast and straightforward to apply. Most time-consuming was the manual evaluation of the peak-picking in all spectra (0.5–3 h). The manual picking of additional peaks and adjusting peak positions depends strongly on the signal overlap especially in the NOESY and HSQC spectra. The Chess2FLYA and FLYA calculations in this paper required 3–5 min of computation time using 20 processors of a Linux cluster system in parallel, and are thus much less time-consuming than currently prevailing manual methods. The FLYA output includes a table of the chemical shift assignments with their assignment confidence (and comparison to previously determined chemical shifts, if available) and summary statistics, as well as a computer-readable chemical shift list and assigned peak lists for all spectra. Manual ‘assignment walks’ can be used to confirm the FLYA assignments. This typically requires about 1 h for the dsRNA regions. More time is required for evaluating the merely tentative FLYA assignments for the non-dsRNA regions. FLYA is also applicable to G•U wobble base pair-containing RNAs resulting in assignments with slightly lower confidence. However, more chemical shift data available in the near future will lead to applicable ¹³C statistics of G•U base-pair environments that will certainly increase the reliability of those assignments.

The automated and assisted assignment methods introduced in this article do not require isotope labeling and are thus ideally suited for various applications. An example is the optimization of RNA constructs for structure determination, e.g. of protein–dsRNA complexes by localizing and monitoring the binding sites on the RNA. H5, H6 and H8 nuclei located in the major groove, and H1′ and H2 nuclei located in the minor groove will be sensitive to binding events. Residues not involved in the binding can be truncated or modified. Such a rational approach might not only be useful for NMR structure determination of complexes but also for X-ray crystallography, since the study of complexes with X-ray crystallography often involves screening of many different RNA constructs in addition to the different crystallization conditions. Another application is the interaction mapping of siRNAs that received much interest recently because of their sequence-specific gene-silencing capability (31). Our method is ideally suited for siRNAs because they consist of Watson–Crick base-paired dsRNA, lack loops and bulges and are of a manageable size of around 40 nt. The 2D statistics could be applied for drug screening: H5–H6 TOCSY signals in characteristic regions (covariance ellipses) corresponding to unique triplets can be followed upon titration of small molecules. This method can be applied also to larger RNAs for which a complete assignment is not required. RNA folding is a further application field: the formation of dsRNA can be followed by the appearance of H5–H6 signals within characteristic chemical shift covariance ellipses.

The automated resonance assignment with FLYA is an important step toward the automatic structure determination of RNA that might be achieved by combining the present approach with automated NOESY assignment (32) and structure calculation (23) as it has been shown for proteins (33). To this end, it may be necessary to assign additional resonances, especially in loop regions, and to reduce the ambiguity of NOE assignments, e.g. by uniform ¹³C/¹⁵N labeling, and experimental and algorithmic developments. Compared with the situation for proteins, where automated structure determination is possible, RNA-specific challenges that will have to be addressed include the generally smaller chemical shift dispersion, the lower density of ¹H nuclei, which results in less dense NOE restraint networks, and the absence or reduced number of potential, truly tertiary structure-determining long-range distance restraints.

An advantage of our chemical shift-based assignment strategies is that, in principle, they can be combined with other approaches, for example with nucleotide-specific ¹³C/¹⁵N labeling (34) in combination with filtered/edited 2D NOESY spectra (35,36). Nucleotide-specific labeling not only allows assigning NMR resonances to a certain nucleotide type, but also provides information about their sequential neighbors and the non-labeled sections. For large RNAs the combination with deuteration methods are promising, e.g. by using samples that are nucleotide-specifically protonated in a deuterated background (37) or samples containing specifically deuterated or/and ¹³C-labeled nucleotides (38–41). Finally, a powerful approach for the assignment of even larger RNAs could be envisaged by combining our strategy with recent developments in segmental isotope labeling of RNAs (42).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Swiss National Science Foundation, National Centre of Competence in Research (NCCR) Structural Biology, SNF Sinergia [CRSII3_127333 to F.H.-T.A.]; Swiss Commission for Technology and Innovation (CTI) [11329.1 PFLS-LS to F.H.-T.A.]; Lichtenberg program of the Volkswagen Foundation [I/81 913 to P.G.]; and Japan Society for the Promotion of Science (JSPS) [to P.G.]. Funding for open access charge: The open access publication charge for this paper has been waived by Oxford University Press - NAR Editorial Board members are entitled to one free paper per year in recognition of their work on behalf of the journal.

Conflict of interest statement. None declared.