Prediction of Protein Essentiality by the Support Vector Machine with Statistical Tests

Abstract

Essential proteins include the minimum required set of proteins to support cell life. Identifying essential proteins is important for understanding the cellular processes of an organism. However, identifying essential proteins experimentally is extremely time-consuming and labor-intensive. Alternative methods must be developed to examine essential proteins. There were two goals in this study: identifying the important features and building learning machines for discriminating essential proteins. Data for Saccharomyces cerevisiae and Escherichia coli were used. We first collected information from a variety of sources. We next proposed a modified backward feature selection method and build support vector machines (SVM) predictors based on the selected features. To evaluate the performance, we conducted cross-validations for the originally imbalanced data set and the down-sampling balanced data set. The statistical tests were applied on the performance associated with obtained feature subsets to confirm their significance. In the first data set, our best values of F-measure and Matthews correlation coefficient (MCC) were 0.549 and 0.495 in the imbalanced experiments. For the balanced experiment, the best values of F-measure and MCC were 0.770 and 0.545, respectively. In the second data set, our best values of F-measure and MCC were 0.421 and 0.407 in the imbalanced experiments. For the balanced experiment, the best values of F-measure and MCC were 0.718 and 0.448, respectively. The experimental results show that our selected features are compact and the performance improved. Prediction can also be conducted by users at the following internet address: http://bio2.cse.nsysu.edu.tw/esspredict.aspx.

Introduction

Identifying essential proteins is important for understanding the cellular processes in an organism because no other proteins can perform the functions of essential proteins. Once an essential protein is removed, dysfunction or cell death results. Thus, several studies have been conducted to identify essential proteins. Experimental approaches for identifying essential proteins include gene deletion,¹ RNA interference,² and conditional knockouts.³ However, these methods are labor-intensive and time-consuming. Hence, alternative methods for identifying essential proteins are necessary.

The essential protein classification problem involves determining the necessity of a protein for sustaining cellular function or life. Among the methods available for identifying essential proteins, machine-learning based methods are promising approaches. Therefore, several studies have been conducted to examine the effectiveness of this technique. Chin⁴ proposed a double-screening scheme and constructed a framework known as the hub analyzer (http://hub.iis.sinica.edu.tw/Hubba/index.php) to rank the proteins. Acencio and Lemke⁵ used Waikato Environment for Knowledge Analysis (WEKA)⁶ to predict the essential proteins. Hwang et al⁷ applied a support vector machine (SVM) to classify the proteins.

Protein-protein interactions (PPIs) are well-known to be significant characteristics of protein function. Several studies have attempted to predict and classify protein function⁸ as well as analyze protein phenotype⁹ by studying interactions. A previous study¹⁰ further suggested that essential proteins and nonessential proteins can be discriminated by means of topological properties derived from the PPI network. In spite of the above superior properties, however, analyzing PPI experimentally is time-consuming. With the advent of yeast two-hybrid¹¹ high-throughput techniques, which can be used to identify several PPIs in one experiment, obtaining PPI information has become easier. Since a PPI network is similar to a social network in many aspects, some researchers apply social network techniques for analyzing PPI networks. Thus, several topological properties have been extensively explored and studied in recent years.

Fundamental properties, such as sequence or protein physiochemical ones, are not subjected to detailed examination in previous studies. This may be because each of these preliminary properties alone is somewhat less relevant to essentiality. However, this information is highly accessible because only sequence information is required to derive these properties. Hence, we included these properties in our study. For topological properties, in addition to physical interactions, we incorporated a variety of interaction information, including metabolic, transcriptional regulation, integrated functional, and genomic context interactions. Our experimental results revealed that these features provide either complement information for essentiality identification or provide other biological justification.

To identify the reduced feature subset, which is crucial for biological processes, previous studies have used feature selection techniques. The advantages of this method include storage reduction, performance improvement or data interpretation.¹² In accordance with whether the feature selection procedure is bound with the predictor, the method is roughly classified into three categories: filter, wrapper, and embedded. Filter methods often provide a complete order of available features in terms of relevance measures. Methods such as Fisher score,¹² mutual information, minimal redundancy and maximal relevance (mRMR),¹³ conditional mutual information maximization (CMIM),¹⁴ and minimal relevant redundancy (mRR)¹⁵ belong to this category. Both wrapper and embedded methods involve the selection process as a part of the learning algorithm. The former utilizes a learning machine to evaluate subsets of features according to some performance measurements. For example, sequential backward and forward feature selection¹² falls into this category. Embedded methods directly perform feature selection in the learning process and they are usually specific to given learning machines. Example include C4.5,¹⁶ Classification and Regression Trees (CART),¹⁷ and ID3.¹⁸ Additionally, some researchers proposed an information-gain based the feature selection method,¹⁹ which examines the effectiveness of classifier combination.

In this paper, we used two datasets. The first one was from Saccharomyces cerevisiae. The corresponding PPI data set was Scere 20070107, which was obtained from the DIP database. The data set totally contains 4873 proteins and 17,166 interactions. Our feature set consisted of the features obtained or extracted from the methods proposed by Acencio and Lemke,⁵ Chin,⁴ Hwang et al,⁷ and Lin et al.²⁰ The second data set was from Escherichia coli, which was first compiled by Gustafson et al.²¹ The data set totally contained 3569 proteins. The associated network information included physical, integrated functional, and genomic context interactions and is collected from Hu et al.²² For both data sets, we propose a modified sequential backward feature selection method for selecting important features.

Next, SVM models were built using the selected feature subsets. In this study, the SVM software LIBSVM²³ was adopted for classification models. Each model was applied to both imbalanced and balanced data sets. The results were compared with those of previous studies and statistical tests were conducted to examine significance. For the imbalanced S. cerevisiae data, our best results for F-measure and MCC were 0.549 and 0.495, respectively, which outperform the best previous method⁷ with results of 0.354 and 0.36, respectively. We obtained values of 0.770 and 0.545 for F-measure and MCC in the balanced data experiment, which was superior to the best previous method⁷ with 0.737 and 0.492, respectively. For experiments examining the E. coli data set, our best values for F-measure and MCC were 0.421 and 0.407, respectively, in the imbalanced data set. In the balanced experiment, the best values for F-measure and MCC were 0.718 and 0.448, respectively. The results are similar to those of Gustafson et al,²¹ who examined 29 features, but in our method, only five or seven features were used for prediction. To verify whether our improvement was statistically significant, we performed bootstrap cross-validation²⁴ on performance measures.

Background

The data set

In this paper, we used two data sets for experiments: S. cerevisiae and E. coli. The former included PPI network data. We downloaded the data set from the DIP ( http://dip.doe-mbi.ucla.edu/) website.²⁵ The original data set contained 4873 proteins and 17166 interactions. To comply with previous studies, we also adopted the largest connected component of the network data. There were a total of 4815 proteins, including 975 essential proteins and 3840 nonessential proteins. The information of protein essentiality was obtained from the Saccharomyces Genome Database (SGD), which is located at http://www.yeastgenome.org/. Since this data set has been used in several previous studies, we thus obtained and incorporated various related features for experiments.

The E. coli data set was obtained from Gustafson et al.²¹ It contained 3569 proteins, among which 611 are essential. Due to availability and coverage issues, we used another information from three additional networks: physical interaction (PI), integrated functional interaction, and integrated PI and genomic context (GC) network. The information was collected from Hu et al.²²

In the above two data sets, the ratio of nonessential proteins to essential proteins was approximately 4:1 and 5:1, respectively. The data imbalance will inevitably led to biased fitting to nonessential proteins during the learning processes. Thus, we constructed another balanced data set. Taking the first data set, for example, we randomly selected 975 nonessential proteins and mixed them with essential proteins to form a balanced data set. In the new data set, the number of nonessential data elements against that of essential elements was equal.

Bootstrap cross-validation

We used bootstrap cross-validation (BCV) to compare the performance of the two classifiers using the k-fold cross-validation. Assume that a sample S = {(x₁, y₁), (x₂, y₂), …, (x_n, y_n)} is composed of n observations, where x_i represents the feature vector of the ith observation and y_i denotes the class label associated with x_i. A bootstrap sample S_b^* = {(x₁^*_,y₁^*),(x₂^*_,y₂^*),…,(x_n^*_,y_n^*)} consists of n observations that are sampled from S with replacement, where 1 ≤ b ≤ B, and B is a constant between 50 and 200. For each sample S_b^*, a k-fold cross-validation was carried out. The performance measure c_b, such as error rate, was calculated with S_b^*. The procedure was repeated B times and then the average performance measure C_B = ∑^B_b=1c_b/B was evaluated over the B bootstrap samples. Since the distribution of the bootstrap performance measures was approximately normal, the confidence interval and significance were estimated accordingly.

Performance measures

In this study, the performance measures included precision, recall, F-measure (F1), Matthews correlation coefficient (MCC), and top percentage of essential proteins. Their formulas are given as follows:

1. Precision: TP/TP + FP

2. Recall: TP/TP + FN

3. F-measure: 2 × precision × recall/(precision + recall)

4. MCC: $\frac{TP\times TN-FP\times FN}{\sqrt{(TP+FN)(TP+FP)(TN+FP)(TN+FN)}}$

5. Top percentage of essential protein: $\frac{Number\hspace{0.17em}of\hspace{0.17em}real\hspace{0.17em}essential\hspace{0.17em}proteins\hspace{0.17em}in\hspace{0.17em}top\hspace{0.17em}n}{n}$.

Here, an essential protein is represented by the positive observation. True positive (TP), true negative (TN), false positive (FP), and false negative (FN) represent the numbers of true positive, true negative, false positive, and false negative proteins, respectively. The value n denotes the total number of predictions. In addition, receiver operating characteristic (ROC) curve¹⁸ and area under curve (AUC) were used to evaluate the classification performance.

Feature extraction

The feature set we used included sequence properties (S), such as amino acid occurrence and average amino acid PSSM; protein properties (P), such as cell cycle and metabolic process; topological properties (T), such as bit string of double screening scheme and betweenness centrality related to physical interactions; and other properties (O), such as phyletic retention and essential index. There were a total of 45 groups and 90 features in the S. cerevisiae data set. For the E. coli data set, there were 35 groups and 80 features. All names and sources are shown in Table 1. Only Bit string of double screening scheme is presented.

Table 1.

Protein features.

ID	Property name	Type	Size	Sub-names	S. cere	E. coli
1	Amino acid occurrence20	S	20	A … Y	•	•
2	Average amino acid PSSM20	S	20	A … Y	•	•
3	Average cysteine position20	S	1		•	•
4	Average distance of every two cysteines20	S	1		•	•
5	Average hydrophobic20	S	1		•	•
6	Average hydrophobicity around cysteine20	S	4	1 … 4	•	•
7	Cysteine count20	S	1		•	•
8	Cysteine location20	S	5	1 … 5	•	•
9	Cysteine odd-even index20	S	1		•	•
10	Protein length20	S	1		•	•
11	Cell cycle5	P	1		•
12	Cytoplasm5	P	1		•
13	Endoplasmic reticulum5	P	1		•
14	Metabolic process5	P	1		•
15	Mitochondrion5	P	1		•
16	Nucleus5	P	1		•
17	Other process5	P	1		•
18	Other localization5	P	1		•
19	Signal transduction5	P	1		•
20	Transport5	P	1		•
21	Transcription5	P	1		•
22	Betweenness centrality related to all interactions41	T	1		•	•
23	Betweenness centrality related to metabolic interactions5	T	1		•
24	Betweenness centrality related to physical interactions5	T	1		•	•
25	Betweenness centrality transcriptional regulation interactions5	T	1		•
26	Bit string of double screening scheme [this paper]	T	1		•	•
27	Bottleneck8,41	T	1		•	•
28	Clique level7	T	1		•	•
29	Closeness centrality42	T	1		•	•
30	Clustering coefficient7	T	1		•	•
31	Degree related to all interactions43	T	1		•	•
32	Degree related to physical interactions5	T	1		•	•
33	Density of maximum neighborhood component4	T	1		•	•
34	Edge percolated component9	T	1		•	•
35	Indegree related to metabolic interaction5	T	1		•
36	Indegree related to transcriptional regulation5	T	1		•
37	Maximum neighborhood component4	T	1		•	•
38	Neighbors’ intra-degree7	T	1		•	•
39	Outdegree related to metabolic interaction5	T	1		•
40	Outdegree related to transcriptional regulation interaction5	T	1		•
41	Betweenness centrality related to integrated functional interaction22	T	1			•
42	Betweenness centrality related to integrated PI and GC network22	T	1			•
43	Degree related to integrated functional interaction22	T	1			•
44	Degree related to integrated PI and GC network22	T	1			•
45	Common function degree7	O	1		•
46	Essential index7	O	1		•
47	Identicalness5	O	1		•
48	Open reading frame length7	O	1		•	•
49	Phyletic retention21	O	1		•	•
50	Number of paralagous genes21	O	1			•
51	Codon Adaptation Index (CAI)21,44	O	1			•
52	Codon Bias Index (CBI)21,44	O	1			•
53	Frequency of optimal codons21,44	O	1			•
54	Aromaticity score21,44	O	1			•
55	Leading strand of the circular chromosome21	O	1			•
	Total		100		90	80

Notes:S. cere and E. coli mean Saccharomyces cerevisiae and Escherichia coli datasets, respectively. For topological features, if not particularly mentioned, they are related to physical interactions. Due to coverage or availability issue, we adopt different features for S. cere and E. coli datasets. For example, interactions in E. coli data set contain integrated functional, PI, and GC network information while those in S. cere include metabolic, transcriptional regulation and PI network information.

Abbreviations: GC, genomic context; PI, physical interactions.

The remaining features are detailed in the Appendix.

Lin et al²⁶ and Chin⁴ proposed the double screening scheme. They used multiple ranking scores to sort essential proteins. The drawback is that each protein does not have a unique score. Thus, we propose a bit string implementation to incorporate these two properties into a single score.

An example of our bit string implementation is shown in Tables 2 and 3. Suppose that four proteins, W, X, Y, and Z, are to be ranked. In the first iteration, we desire to find the top one protein. We first select the top 2 proteins using the ranking method A, which are W and X. Next, we use method B to rank these two proteins. The ranks of W and X are 2 and 1, respectively. Hence, in the first iteration, X is finally selected. It follows the bit M [X, 1] is set to 1, and others, M [W, 1], M [Y, 1] and M [Z, 1], are set to 0. In the second iteration, 2 top-ranking proteins are to be found. First, four proteins W, X, Y and Z are selected, because they are the top 4 proteins by ranking method A. Next, with ranking method B, we select the top 2 proteins from them, which are X and Y. Hence, the bits corresponding to M [X, 2] and M [Y, 2] are set to 1, and the others are set to 0 in this iteration. Finally, we sum up the bits of each protein, as shown in the fourth column of Table 3.

Table 2.

Ranking by two different methods, where smaller numbers indicate higher ranks.

Protein name	Ranking method
	A (DMNC)	B (MNC)
W	1	4
X	2	2
Y	3	1
Z	4	3

Table 3.

Bit strings by the double screening method.

Protein name	i th iteration		Sum of bit string	n – r	Sum
	1st	2nd
W	0	0	0	0	0
X	1	1	2	2	4
Y	0	1	1	3	4
Z	0	0	0	1	1

There is still an issue in the bit string implementation, that is, M may be too sparse to be handled by classifiers. Since the number of proteins being selected is around n/2, the sum of about n/2 bits is close to 0. In our experience, this makes it difficult to distinguish between proteins. To overcome this problem, for each protein, we added another score n – r to the sum of the bit string, where r is the rank of the protein by the ranking method B. In this study, we used DMNC to rank A and MNC to rank B. In this example, n = 4, so the values n – r of W, X, Y and Z are 0, 2, 3, and 1, respectively. We summed the values with the bit string; hence, the final scores are 0, 4, 4, and 1. The overall procedure is given in the Procedure bit string implementation of DSS.

Sequential backward feature selection method

SVM is a well-established tool for data analysis which has been shown to be useful in various fields, such as text summarization,²⁷ intrusion detection,²⁸ and image coding.²⁹ In this study, we utilized the SVM software developed by Chang and Lin, called LIBSVM.²³ To address the data imbalance, we propose the modified sequential backward feature selection method.

Since most data were nonessential, choosing only accuracy as an objective or adopting conventional feature ranking schemes favored negative data. As more and more features were excluded, overall accuracy declined. Since the number of negative data elements was higher than that of positive factors, the true-positive rate thus decreased more than the true-negative rate. Thus, features should be selected that most positive samples are correctly classified while not deteriorating the overall accuracy too much. In this sense, rather than using only accuracy to guide the feature selection, we used a composite score C as the objective function. The composite score was represented in terms of precision (P), recall (R), F-measure (F), and MCC (M) and was given as C = w_P * P + w_R * R + w_F * F + w_M * M. The four adjustable weights, w_P, w_R, w_F, and w_M, were used, leading to compromise among the associated performance measures. An additional punishment was imposed to C to allow scores associated with fewer features could compete with those with more features. That is,

$$C(S)=w_P*P(S)+w_R*R(S)+w_F*F(S)+w_M*M(S)\times (|S|-t)*u(|S|-t)*e,$$

where S denotes the selected feature subset. |S| and t denote the size of S and the goal number of features specified by a user, respectively. The unit step function u(|S| – t) = 0 as |S| – t ≤ 0, otherwise u(|S| – t) = 1. Finally, a threshold ρ was adopted to make ensure that the improvement over feature changes was not a random process. The value of ρ was estimated by comparing average score difference among feature subsets of sizes p and p + 1 in the preliminary run for given several different values of p. The value e denotes the penalty score when an additional feature is selected. The score is also specified by the user and should be slightly larger than ρ to encourage feature subsets of smaller sizes. The procedure for feature selection is described in Procedure backward feature selection.

Procedure: Bit String Implementation of DSS
input: P: proteins for ranking, where |P| = n
           A: ranking methods, where |A| = m = 2
          M: bit matrix of $n\times \frac{n}{2}$, initialized by 0
output: Protein ranking scores R
begin
    fori = 1 tondoR[i] = 0;
    fori = 1 to |_n/2_| do
        T1 = top 2i proteins ranked by A(1) in P;
        T2 = top i proteins ranked by A(2) in T1;
        foreachx ∈ T2doM [x, i] = 1;
    end
    fori = 1 tondo
        foreachj = 1 to |_n/2_| doR[i] = R[i]
       + M [i, j];
       end
       T = protein orders ranked by A(m) ;
       foreachi = 1 tondoR[i] = R[i] + (n − T [i])
end

Experimental procedure and results

For comparison purposes, we used two feature selection methods: mRMR and CMIM. In the S. cerevisiae data set, our results were also compared to those of Acencio and Lemke⁵ and Hwang et al.⁷ For the E. coli data set, we also compared our results with those of Gustafson et al.²¹

Procedure: Backward Feature Selection
input :e: penalty score
            k: number of folds for cross-validation
            r: maximal number of rounds to retry
           S0: set of all available features, where |S0| = n
           t: goal number of selected features
           wP, wR, wF and wM: weights of performance measures
           ρ: minimal improvement to proceed
output: Selected feature subset S
data: 50% of all available data elements
begin
    S = S0;
    ift ≥ nthen stop elsem = n − t;
    forp = 1 tomdo
            improved = False ;
            fori = 1 tordo
                 Conduct k-fold CV and calculate C (S);
                 foreachs ∈ Sdo
                      Conduct k-fold CV and calculate C
                      (S – {s});
                 end
                 q = argmaxs∈S {C (S – {s}) – C (S)};
                 ifC (S - {q}) – C (S) ≥ ρthen
                    S = S - {q};
                     improved = True;
                     break;
                 end
            end
             ifnot improvedthen stop and output S
    end
end

Experimental procedure

The overall procedure of our experiments is illustrated in Figure 1 and is described as follows.

Figure 1.

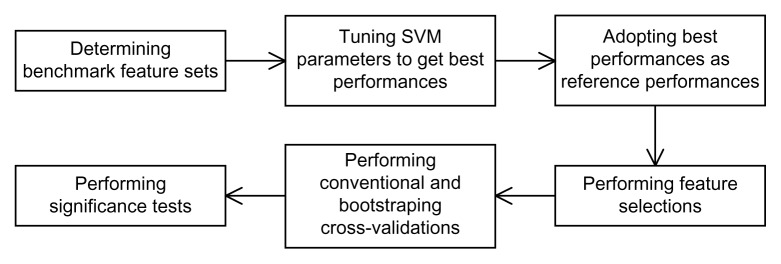
Flowchart for the construction of SVM models and performance comparison.

Stage 1: Determine benchmark feature set

For the S. cerevisiae data set, we used Hwang’s feature set as the benchmark. For the E. coli data set, we used Gustafson’s feature set as the benchmark. These two feature sets are considerably effective for various performance measures.

Stage 2: Tune SVM parameters for best performance

For the above two feature sets, we first ran the SVM software using the feature sets of Hwang or Gustafson and tuned the SVM parameters to achieve the highest average performances.

Stage 3: Adopt best performances as reference performances

After determining the best SVM parameters for the feature sets of Hwang and Gustafson, we recorded the SVM parameters and results. To compare our results with other models, such as those obtained using our methods, mRMR and CMIM, we used the same SVM software and adjust the cost parameters of SVM in order to achieve similar levels of precision.

Stage 4: Perform feature selection

We randomly chose 50% of available data. Next, the backward feature selection procedure was applied to these selected data. In the beginning of our feature selection procedure, we imposed no penalty on the score calculation. Hence, the procedure attempts to achieve the highest score. In the subsequent runs, we added penalties for feature sizes to the score calculation. Subsets with smaller feature size but only slightly inferior in performance were selected. To compare our results with those of other methods, we also used the mRMR and CMIM feature ranking methods and chose subsets as in Procedure backward feature selection.

Stage 5: Perform 10-fold and bootstrap cross-validations

The data were prepared in both balanced and imbalanced manners. For each data set, we randomly partitioned all data into 10 disjoint groups and used the feature subsets selected in the previous stage to calculate various performance measures. The data were prepared in both balanced and imbalanced manners. The 10-fold cross validation was repeated 10 times and average performance measures were computed. Next, a bootstrap sampling procedure was conducted and 200 bootstrap samples were produced, including both balanced and imbalanced samples. Each bootstrap sample was also partitioned for 10-fold cross validations and performance measures were calculated. Note that all models were examined by the same sets of data partitions for conventional and bootstraping cross-validations.

Stage 6: Perform significance tests

Once bootstrap cross validations were carried out, the significance tests were adopted accordingly. In addition to the average values of AUC, precision, recall, F-measure, and MCC, we conducted a statistical significance test for these performance measures. Additionally, we calculated ROC curves and top percentage values for imbalanced experiments.

Backward feature selection and mRMR/CMIM feature ranking

We used 50% of available data elements for feature selection. Taking the S. cerevisiae data set as an example, only (3840 + 975) × 50% observations were randomly chosen for the Backward feature selection procedure. During the procedure, several performance scores were calculated by means of k-fold cross-validations. In the first run, the parameters were set as follows: k = 2, w_P = 1, w_R = 1, w_F = 1, w_M = 1, ρ = 0.005, e = 0, t = 0, and r = 5. Since all associated weights were equal, the procedure sought the best compromise among all performance measures. t = e = 0, meaning that no goal number of selected features was imposed, giving the procedure opportunities to exploit all available feature combinations to achieve the best performance. In this initial run, we obtained a feature subset of 18 in size.

For the subsequent runs, the value of t was decreased starting from 17 (= 18 – 1) until performances were significantly worse than those of Hwang et al.⁷ In order to obtain feature subsets of reduced sizes, parameters were set: k = 2, w_P = 1.03, w_R = 1, w_F = 1, w_M = 1, ρ = 0.005, e = 0.01, and r = 5. The reason for setting w_P = 1.03 was to prevent the true positive rate from decreasing too much. In addition, e > ρ was to allow the procedure to be proceeded to fewer features. The above settings were used to encourage selection of reduced feature subsets.

For each setting of t, we executed the procedure 10 times with different k-fold partitions and obtained 10 feature subsets of the same size. Since these 10 resultant feature subsets were slightly different, we performed another 5-fold cross-validation with these feature subsets and compared their performance scores. The one with the highest score were finally preserved as our feature subset.

In addition to the methods of Hwang et al or Gustafson et al,²¹ we also used mRMR¹³ and CMIM¹⁴ feature selection methods for comparison. Using mRMR as an example, the data used in our feature selection procedure were input into the mRMR program, which produced the ranking score of each feature. The feature with the least score was removed first and a subsequent 5-fold cross-validation with the preserved features is performed to calculate the composite score C (S). That is, in the ith iteration, the features with the lowest i ranking scores were removed and C (S) was calculated. The removal and cross-validation procedure was repeated until no feature was preserved. The entire process (including random choice of 50% data and feature removal) was executed 10 times and the feature subset of the same size with the highest score was recorded.

Table 4 shows the selected feature subsets of different sizes for S. cerevisiae data. The second column of the table lists all selected features. Each N_i in the first row represents the feature subset of size i, 4 ≤ i ≤ 18, which was found using our backward feature selection procedure. For each feature subset N_i, a bullet (•) mark below in the same column was used to indicate which feature was included. The most competent feature subsets selected by CMIM and mRMR were denoted by C32 and m31, which means that 32 and 31 features were selected, respectively. It is observed that a total of 60 features have been selected, which represent the prominent proteins used to identify essential proteins.

Table 4.

Selected features for S. cerevisiae data set.

	Feature	N5	N6	N7	N8	N9	N10	N11	N12	N13	N14	N15	N16	N17	N18	m31	C32	TOT
1	PR (phyletic retention)	•	•	•	•	•	•	•	•	•	•	•	•	•	•	•	•	16
2	EI (essentiality index)	•	•	•	•	•	•	•	•	•	•	•	•	•	•	•	•	16
3	Cytoplasm	•	•	•	•	•	•	•	•	•	•	•	•	•	•		•	15
4	Nucleus	•	•	•	•	•	•	•	•	•		•	•	•	•	•	•	15
5	Occurrence of A.A. I			•	•	•	•	•	•	•	•	•	•	•	•		•	13
6	Bit string of DSS		•	•	•	•	•	•	•		•	•	•	•	•			12
7	Occurrence of A.A. W				•	•	•	•	•	•	•	•	•	•	•		•	12
8	Endoplasmic reticulum					•	•	•	•	•	•	•	•	•	•	•		11
9	Other process										•	•	•	•	•	•	•	7
10	Occurrence of A.A. S								•		•		•	•	•	•	•	7
11	Occurrence of A.A. G							•		•		•	•	•	•			6
12	KLV (clique level)								•	•	•		•			•	•	6
13	Cell cycle								•		•		•			•	•	5
14	Average hydrophobic									•		•		•	•		•	5
15	Average PSSM of A.A. R						•	•				•		•	•			5
16	B.C. related to PI									•				•	•	•		4
17	Occurrence of A.A. E									•			•			•	•	4
18	Average PSSM of A.A. P						•	•				•					•	4
19	ID related to T.R.													•	•	•		3
20	B.C. T.R. interactions											•			•	•		3
21	Other localization													•	•		•	3
22	DMNC	•	•														•	3
23	Average HYD around C-2								•		•		•					3
24	Signal transduction													•	•			2
25	Edge percolated component															•	•	2
26	Occurrence of A.A. P															•	•	2
27	Occurrence of A.A. T				•	•												2
28	Occurrence of A.A. Y															•	•	2
29	Average PSSM of A.A. Q									•							•	2
30	Average PSSM of A.A. E										•		•					2
31	CLC (clustering coefficient)															•	•	2
32	FunK (common function degree)															•	•	2
33	OD related to T.R. interaction															•		1
34	OD related to M.I.															•		1
35	ID related to M.I.															•		1
36	B.C. related to M.I.															•		1
37	Degree related to PI																•	1
38	Metabolic process															•		1
39	Bottleneck															•		1
40	MNC															•		1
41	Occurrence of A.A. A																•	1
42	Occurrence of A.A. C															•		1
43	Occurrence of A.A. D																•	1
44	Occurrence of A.A. H															•		1
45	Occurrence of A.A. K																•	1
46	Occurrence of A.A. M															•		1
47	Average C position																•	1
48	Protein length															•		1
49	Cysteine count																	1
50	Cysteine odd-even index			•												•		1
51	Average HYD around C-1										•							1
52	Cysteine location-1															•		1
53	Average PSSM of A.A. A											•						1
54	Average PSSM of A.A. D																•	1
55	Average PSSM of A.A. S																•	1
56	Average PSSM of A.A. W																•	1
57	Average PSSM of A.A. Y																•	1
58	ORFL (ORF length)																•	1
59	CC (closeness centrality)																•	1
60	BC (B.C.)															•		1

Abbreviations: DSS, double screening scheme; A.A., amino acid; B.C., betweenness centrality; T.R., transcriptional regulation; HYD, hydrophobicity; PI, physical interaction; A … Y, amino acid abbreviation; M.I., metabolic interaction; OD, outdegree; ID, indegree; m31, mRMR31; C32, CMIM32; FunK, Common function degree; TOT, total.

After the feature subsets were selected, to conduct performance comparison as well as to cope with the randomness, we used Hwang’s method to perform 10 10-fold cross-validations. Here, the true positive rates and false positive rates were input into a diferent software program to calculate ROC curves and AUC values. In this study, the software package we used is ROCR, which was developed by Tobias et al.^30,31 Thus, the reported performance measures, including AUC, F1, MCC, precision, and recall values and ROC curves, were averaged over 10 10-fold cross-validations.

For the S. cerevisiae data set, the predictor with Hwang’s 10 features served as a benchmark because it yielded distinguished results in terms of feature size and performance. Additionally, mRMR or CMIM were adopted for comparison.

We appled the same procedure for the E. coli data set. The selected features are shown in Table 5, with a total of 43 features selected. In the table, feature subsets selected by CMIM and mRMR are denoted by C9 and m13, meaning that 9 and 13 features were selected, respectively.

Table 5.

Selected features for E. coli data set.

	Feature	N4	N5	N6	N7	N8	N9	N10	N11	N12	N13	C9	m13	TOT
1	PR (phyletic retention)	•	•	•	•	•	•	•	•	•	•	•	•	12
2	Open reading frame length		•		•	•	•	•	•	•	•			8
3	Average PSSM of A.A. C	•	•	•	•	•					•			6
4	Degree related to F.I.	•	•	•	•	•					•			6
5	Degree related to A.I.						•	•	•	•		•		5
6	Degree related to PI						•	•	•	•			•	5
7	Average PSSM of A.A. A				•	•						•	•	4
8	Average PSSM of A.A. R						•	•	•	•				4
9	Average hydrophobic						•	•	•	•				4
10	Bit string of DSS for PI						•	•	•	•				4
11	Paralog count			•						•	•		•	4
12	Occurrence of A.A. M					•	•			•				3
13	Occurrence of A.A. W							•			•	•		3
14	Occurrence of A.A. E		•	•										2
15	Occurrence of A.A. F								•			•		2
16	Occurrence of A.A. G						•		•					2
17	Occurrence of A.A. I											•	•	2
18	Average PSSM of A.A. Y					•			•					2
19	Cysteine location-4											•	•	2
20	KLV (clique level) for PI				•						•			2
21	Degree related to PI and GC								•	•				2
22	Strand bias									•			•	2
23	Occurrence of A.A. A							•						1
24	Occurrence of A.A. C											•		1
25	Occurrence of A.A. H											•		1
26	Occurrence of A.A. P			•										1
27	Occurrence of A.A. S							•						1
28	Average PSSM of A.A. N										•			1
29	Average PSSM of A.A. G										•			1
30	Average PSSM of A.A. K				•									1
31	Average PSSM of A.A. F					•								1
32	Average PSSM of A.A. T										•			1
33	Average PSSM of A.A. V										•			1
34	Average distance of every two Cs									•				1
35	Average HYD around C-2										•			1
36	Cysteine location-1												•	1
37	Cysteine location-5												•	1
38	Cysteine odd-even index												•	1
39	Protein length	•												1
40	Bottleneck for PI												•	1
41	CC (closeness centrality) for PI												•	1
42	MNC for PI										•			1
43	B.C. related to all F.I.												•	1

Abbreviations: C9, CMIM09; m13, mRMR13; TOT, total; DSS, double screening scheme; F.I., integrated functional interaction; A.I., all interactions. PI, physical interaction; HYD, hydrophobicity; A.A., amino acid; A … Y, amino acid abbreviation.

Bootstrap cross validations

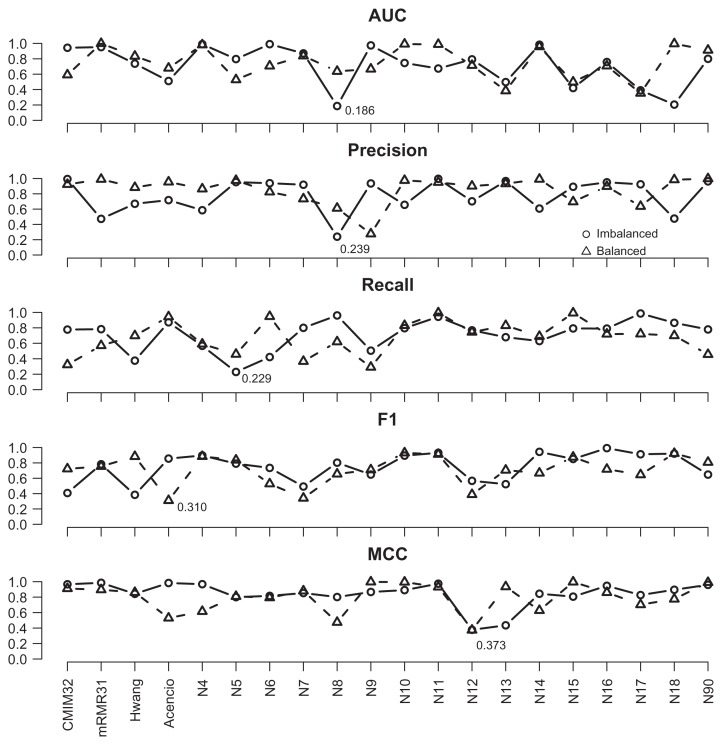
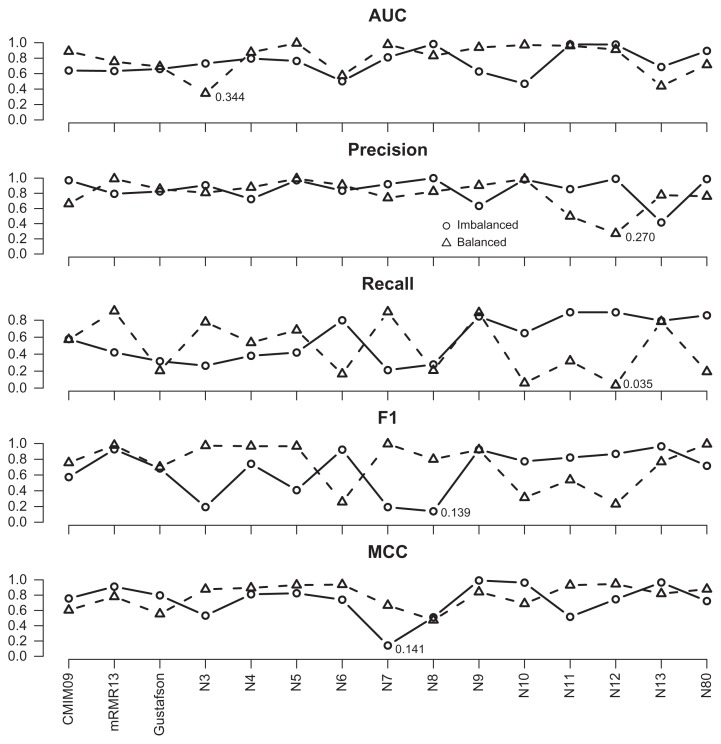
During the bootstrapping stage, for each bootstrap sample, an identical 10-fold partition was employed for all feature subsets to carry out cross-validations and compute various average performance measures. The procedure was repeated for 200 distinct bootstrap samples. In order to perform parametric significance tests, we evaluated whether the distribution of the resultant performance measures was normal and the variances obtained from different feature subsets were similar. Consequently, 200 results of each performance measure for each feature subset were subjected to the Kolmogorov-Smirno test.³¹ This test examines the null hypothesis that no systematic difference exists between the standard normal distribution and the underlying distribution against the alternative one that asserts a systematic difference. The threshold was set to 0.05. If the P-value was less than 0.05, we rejected the null hypothesis. For CMIM and mRMR, only the most prominent values are shown. Figures 2 and 3 illustrate the results for S. cerevisiae and E. coli data sets, respectively, in which the test values were recorded according to the feature subsets, performance measures, and experiment types. For the S. cerevisiae data set, the lowest P-value, 0.186, was observed for AUC of the N8-imbalanced experiment. Therefore, it is likely that there was no significant difference between the normal distribution and the distribution of every performance measure of each feature subset. For the E. coli data set, most performance measures were normal with the exception of the recall values associated with N12-balanced (with P-value = 0.035), for which comparing results were not reliable. For the performance measures associated with each model, we also listed their confidence interval and information odds ratios,³² which are shown in the Appendix.

Figure 2.

The P-value of the normality test in S. cerevisiae data set.

Figure 3.

The P-value of the normality test in S. cerevisiae data set.

For a certain performance measure, since the variances obtained by various feature subsets were quite similar, we used an analysis of variance³³ (ANOVA) test to examine whether differences existed among performance measures of different feature subsets. Here, one variance can be obtained from the multiple experiments with a feature subset. Differences existed according to the ANOVA. Next, all of these measures were compared with their associated benchmark to calculate performance deviations. The average deviation corresponding to each type of performance measure was evaluated using the 95% confidence interval covering 0 to determine significance.

Performance comparison and significance tests

In this section, we compared our experimental results with those associated with other feature selection methods and previous studies. For conciseness, we only show the most prominent results associated with mRMR and CMIM. We observed that feature sizes identified by these two methods were relatively large. To compare the feature subsets of smaller sizes, their comparison and their working principles are detailed in the Appendix.

S. cerevisiae

Table 6 lists the average values of five performance measures associated with a variety of feature subsets, which were obtained by 10 10-fold cross-validations for imbalanced data. We adjusted the SVM cost parameters in order to achieve similar levels of precision. The first four rows show results of CMIM32 (32 features), mRMR31 (31 features), Hwang’s (10 features), and Acencio’s (23 features). Values following these items are enclosed by parentheses and represent the numbers of features. Results produced by our method are listed in the subsequent rows of the table. Significance tests were carried out with the bootstrap cross-validations over 200 bootstrap samples. The first three symbols, which can be plus (+) or minus (−), following each numerical value represents significantly higher or lower than benchmark results. For those which serve as benchmarks are marked by star (*) symbols for clarity. For example, the recall of N6 was significantly higher than that of Hwang, while its AUC was significantly lower than those of mRMR31 and Hwang. For the feature subsets with a prefix name ‘N’, their fourth symbols behind numerical values are used to indicate the significance between two neighboring rows. For example, for N7, its AUC was significantly higher than that of N6 and its recall value was also significantly higher than that of N8. For values of the same performance measure in each column, the best is underlined. Values in the last row show the results with the full set of 90 features.

Table 6.

Performance comparison for the imbalanced S. cerevisiae data set.

	AUC					Precision					Recall					F-measure					MCC
CMIM32	0.825	*	(+)	(+)		0.744	*		(+)		0.369	*		(+)		0.493	*		(+)		0.450	*		(+)
mRMR31	0.821	(−)	*	(+)		0.738		*			0.372		*	(+)		0.495		*	(+)		0.449		*	(+)
Hwang(10)	0.775	(−)	(−)	*		0.743	(−)		*		0.343	(−)	(−)	*		0.469	(−)	(−)	*		0.432	(−)	(−)	*
Acencio(23)	0.707	(−)	(−)	(−)		0.675	(−)	(−)	(−)		0.121	(−)	(−)	(−)		0.204	(−)	(−)	(−)		0.228	(−)	(−)	(−)
N4	0.744	(−)	(−)	(−)		0.782					0.327	(−)	(−)	(−)		0.461	(−)	(−)	(−)		0.439	(−)	(−)
N5	0.727	(−)	(−)	(−)		0.741	(−)			(−)	0.387	(−)	(−)		(+)	0.509	(−)	(−)		(+)	0.461	(−)	(−)		(+)
N6	0.730	(−)	(−)	(−)		0.752	(−)				0.395	(−)	(−)	(+)		0.518	(−)	(−)			0.472	(−)	(−)
N7	0.761	(−)	(−)		(+)	0.767	(−)				0.386	(−)	(−)	(+)		0.513	(−)	(−)	(+)		0.473	(−)	(−)
N8	0.772	(−)	(−)			0.755					0.371	(−)	(−)		(−)	0.498	(−)	(−)	(+)	(−)	0.457	(−)	(−)		(−)
N9	0.782	(−)	(−)	(+)		0.749					0.382	(−)		(+)	(+)	0.506	(−)		(+)		0.462	(−)		(+)
N10	0.781	(−)	(−)	(+)		0.751					0.399			(+)		0.521			(+)		0.474			(+)
N11	0.786	(−)	(−)	(+)		0.752					0.402			(+)		0.524			(+)		0.476			(+)
N12	0.798	(−)	(−)	(+)		0.759					0.409			(+)		0.532			(+)		0.485			(+)
N13	0.789	(−)	(−)	(+)		0.748					0.433			(+)	(+)	0.549			(+)		0.495			(+)
N14	0.802	(−)		(+)		0.749					0.397			(+)	(−)	0.519			(+)	(−)	0.471			(+)	(−)
N15	0.801	(−)		(+)		0.763					0.406			(+)		0.530			(+)		0.485			(+)	(+)
N16	0.814	(−)		(+)	(+)	0.762					0.401			(+)		0.525			(+)		0.480			(+)
N17	0.814	(−)		(+)		0.761					0.407			(+)		0.530			(+)		0.484			(+)
N18	0.811	(−)		(+)		0.751					0.411			(+)		0.531			(+)		0.482			(+)
N90	0.829	(+)	(+)	(+)	(+)	0.738		(+)	(+)		0.355		(+)	(+)	(−)	0.479	(+)	(+)	(+)	(−)	0.438	(+)	(+)	(+)	(−)

Note: With the polynomial kernel function, the values of precision, recall and MCC are reported as 0.77, 0.23, and 0.36, respectively, in the original paper of Hwang et al.⁷

Based on Table 6, CMIM32, mRMR31 and Hwang’s predictors outperformed Acencio’s in all performance measures. For our feature subsets, the performance measures were slightly higher than Hwang’s. For those of N8, there was no performance difference from Hwang’s in AUC, while the remaining measure values were higher than Hwang’s. When the feature size exceeded 8, except for precision values, improvement over Hwang’s was consistently significant in most cases. For comparison with mRMR, our method performed nearly as well as mRMR31 when the feature size was between 9 and 13 with the exception of AUC values. When the feature size ranged from 14 to 18, there was no performance difference between our model and mRMR31. The most prominent predictor was CMIM32. Except for AUC values, our results achieved similar levels of performance when the size of features exceeded 14. Note that the number of features in CMIM32 and mRMR31 were 32 and 31, which was much higher than ours.

Table 7 shows the average performance measures in balanced experiments of the S. cerevisiae data set, which were also obtained via 10 10-fold cross-validations. For those of our feature subsets with size ranging from 5 to 18, nearly all performance measures were the same as or higher than those of Hwang’s. This shows that the feature subsets with sizes exceeding 5 are at least as good as Hwang’s. Additionally, those with 12 or more features achieved significant improvement. Compared with CMIM32 and mRMR31, our results showed similar levels of performance when the size of features exceeded 15. The results with the full set of 90 features are shown in the last row, whose performance measures were similar to those from N14 to N18.

Table 7.

Performance comparison for the balanced S. cerevisiae data set.

	AUC					Precision					Recall					F-measure					MCC
CMIM32	0.842	*		(+)		0.772	*				0.766	*		(+)		0.769	*		(+)		0.540	*		(+)
mRMR31	0.836		*	(+)		0.765		*			0.741		*	(+)		0.752		*	(+)		0.513		*	(+)
Hwang(10)	0.822	(−)	(−)	*		0.778			*		0.720	(−)	(−)	*		0.748	(−)	(−)	*		0.516	(−)	(−)	*
Acencio(23)	0.768	(−)	(−)	(−)		0.696	(−)	(−)	(−)		0.734	(−)	(−)			0.714	(−)	(−)	(−)		0.414	(−)	(−)	(−)
N4	0.811	(−)	(−)	(−)	(+)	0.777		(−)		(+)	0.716	(−)	(−)			0.745	(−)	(−)		(+)	0.512	(−)	(−)		(+)
N5	0.824	(−)	(−)		(+)	0.778		(−)			0.735	(−)	(−)		(+)	0.756	(−)	(−)			0.527	(−)	(−)
N6	0.827	(−)	(−)		(+)	0.778		(−)			0.739	(−)	(−)			0.758	(−)	(−)			0.530	(−)	(−)
N7	0.831	(−)	(−)			0.779					0.733	(−)	(−)			0.755	(−)	(−)			0.526	(−)	(−)
N8	0.826	(−)	(−)			0.786					0.721	(−)	(−)			0.752	(−)	(−)			0.527	(−)	(−)
N9	0.833	(−)	(−)		(+)	0.791					0.735	(−)	(−)		(+)	0.762	(−)	(−)			0.541	(−)	(−)
N10	0.834	(−)	(−)			0.789					0.736	(−)	(−)			0.761	(−)	(−)			0.540	(−)	(−)
N11	0.831	(−)	(−)			0.784					0.737	(−)	(−)			0.760	(−)	(−)			0.535	(−)	(−)
N12	0.829	(−)	(−)			0.779					0.732					0.755			(+)		0.526			(+)
N13	0.834	(−)	(−)			0.788					0.730	(−)	(−)			0.758	(−)	(−)			0.535	(−)	(−)
N14	0.836	(−)	(−)	(+)		0.777					0.743	(−)	(−)	(+)		0.759	(−)	(−)	(+)		0.530	(−)	(−)
N15	0.843	(−)	(−)	(+)		0.784					0.748	(−)	(−)	(+)		0.766		(−)	(+)		0.542		(−)	(+)
N16	0.842			(+)		0.777					0.756			(+)		0.767			(+)		0.540			(+)
N17	0.847			(+)		0.778					0.763			(+)		0.770			(+)		0.545			(+)
N18	0.840	(−)	(−)	(+)	(−)	0.779		(−)			0.740	(−)	(−)	(+)	(−)	0.759	(−)	(−)			0.531	(−)	(−)
N90	0.839	(+)		(+)		0.760					0.753			(+)		0.757			(+)		0.516			(+)

Note: In the original paper of Hwang et al⁷ the values of precision, recall, F-measure and MCC are reported as 0.763, 0.713, 0.737, and 0.492, respectively, with the polynomial kernel function.

In Table 6, we can observe that feature subsets N5, N7, N9, N13, N15, and N16 showed significant improvement in performance but were smaller in feature sizes when compared with neighboring rows. In Table 7, the significant subsets were N5, N6, and N9. In addition, as shown in Tables 6 and 7, our models performed equally well as CMIM32 and mRMR31 when the feature size was 16 or 17. We used N5, N9, and N16 to draw ROC curves.

E. coli

Tables 8 and 9 shows the average values of five performance measures associated with a variety of feature subsets, which were obtained by 10 10-fold cross-validations for imbalanced and balanced experiments, respectively. The first two rows show results of CMIM09 (9 features) and Gustafson’s (29 features).

Table 8.

Performance comparison for imbalanced E. coli data set.

	AUC				Precision					Recall					F1					MCC
CMIM09	0.701	*		(−)	0.720	*				0.271	*		(−)		0.394	*		(−)		0.382	*		(−)
mRMR13	0.715		*	(−)	0.713		*			0.250		*	(−)		0.370		*	(−)		0.360		*	(−)
Gustafson(29)	0.711	(+)	(+)	*	0.720			*		0.290	(+)	(+)	*		0.420	(+)	(+)	*		0.413	(+)	(+)	*
N4	0.691	(−)	(−)	(−)	0.725					0.280	(+)		(−)	(−)	0.404	(+)		(−)		0.391			(−)
N5	0.690	(−)	(−)	(−)	0.737					0.295	(+)	(+)		(+)	0.421	(+)	(+)	(−)	(+)	0.407	(+)		(−)	(+)
N6	0.701			(−)	0.742					0.287	(+)	(+)			0.414	(+)	(+)			0.403	(+)	(+)
N7	0.714			(−)	0.735					0.275	(+)	(+)	(−)		0.400	(+)	(+)	(−)		0.392	(+)
N8	0.705			(−)	0.742					0.288	(+)	(+)	(−)	(+)	0.415	(+)	(+)	(−)	(+)	0.405	(+)		(−)
N9	0.707			(−)	0.726				(−)	0.293	(+)	(+)			0.417	(+)	(+)			0.401	(+)	(+)
N10	0.711			(−)	0.724					0.294	(+)	(+)			0.418	(+)	(+)			0.401	(+)	(+)
N11	0.714			(−)	0.732					0.278	(+)	(+)		(−)	0.403	(+)	(+)			0.393	(+)	(+)
N12	0.712	(+)			0.725					0.292	(+)	(+)			0.416	(+)	(+)			0.400	(+)	(+)
N13	0.714	(+)			0.733					0.287	(+)	(+)			0.413	(+)	(+)			0.400	(+)	(+)
N80	0.716	(+)	(+)	(+)	0.677	(+)	(+)	(+)	(−)	0.237	(+)	(+)		(−)	0.352	(+)	(+)		(−)	0.339	(+)	(+)	(+)	(−)

Table 9.

Performance comparison for balanced E. coli data set.

	AUC					Precision				Recall					F1					MCC
CMIM09	0.767	*	(+)			0.720	*			0.700	*	(+)			0.710	*	(+)			0.421	*
mRMR13	0.762	(−)	*	(−)		0.728		*		0.654	(−)	*	(−)		0.689	(−)	*	(−)		0.396	*	(−)
Gustafson(29)	0.777		(+)	*		0.722			*	0.715		(+)	*		0.719		(+)	*		0.440	(+)	*
N4	0.780		(+)			0.733				0.701		(+)			0.717		(+)			0.446	(+)
N5	0.779		(+)			0.730				0.706		(+)			0.718		(+)			0.445	(+)
N6	0.762			(−)	(−)	0.735				0.663			(−)	(−)	0.696					0.425
N7	0.783		(+)		(+)	0.737				0.696		(+)			0.716		(+)		(+)	0.448	(+)
N8	0.781		(+)			0.723				0.711		(+)			0.717		(+)			0.439	(+)
N9	0.782		(+)			0.715				0.703		(+)			0.709		(+)			0.423
N10	0.781		(+)			0.725				0.702		(+)			0.713		(+)			0.436	(+)
N11	0.777		(+)			0.719				0.700		(+)			0.709		(+)			0.426
N12	0.776		(+)			0.715				0.695		(+)			0.705		(+)			0.418
N13	0.776		(+)			0.731				0.695		(+)			0.712		(+)			0.439	(+)
N80	0.769					0.711				0.715		(+)		(+)	0.713		(+)			0.424

Table 8 shows that Gustafson’s predictors outperformed CMIM09 in most performance measures in imbalanced experiments. For our feature subsets, the performance measures were slightly higher than CMIM09. When the feature size exceeded 6, the improvement over CMIM09 was consistently significant. To compare Gustafson’s method with our method, ours almost performed as well as Gustafson’s when the feature size was over 11. Note that the number of features in Gustafson’s was 29, which was higher than ours. Table 9, except for the least effective predictor mRMR13, shows almost no performance difference among most feature subsets in balanced experiments. For further ROC analysis, in addition to CMIM09, mRMR13, and Gustafson’s, we further used N4, N8, N11 and N80 to draw ROC curves. This is because we observed performances of insufficient, middle and full feature sets.

ROC analysis

S. cerevisiae

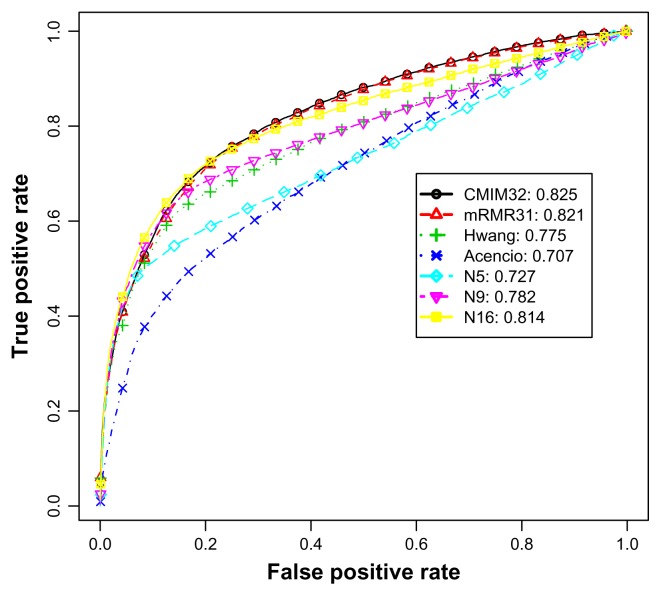
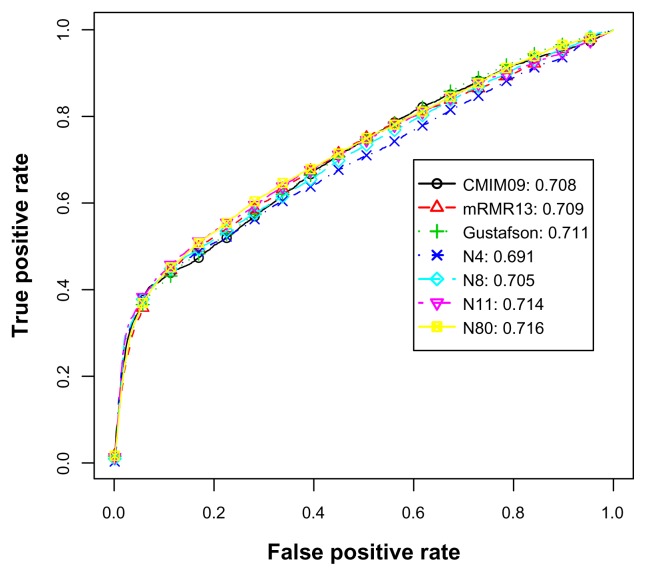
Figure 4 illustrates the average ROC curves and AUCs of various feature subsets for the imbalanced data experiments. Apart from the most competent predictor CMIM32, although the AUC of N5 is higher than that of Acencio’s, an intersection can be observed at 0.5 on the horizontal axis. This indicates that N5 was a better predictor when the allowed maximal false positive rate was below 0.5. In contrast, when the allowed false positive rate exceeded 0.5, Acencio’s was better than N5. Comparing N9 and Hwang’s method, both AUC values were similar. For the feature subsets with sizes exceeding 8 (not all shown in this figure), all true positive rates were either higher or at least close to Hwang’s. This was also supported by the significance tests in Table 6 and suggests that the feature subsets with sizes exceeding 8 achieved higher performance in AUC than Hwang’s predictor.

Figure 4.

The average ROC curves and AUCs for the imbalanced S. cerevisiae data set.

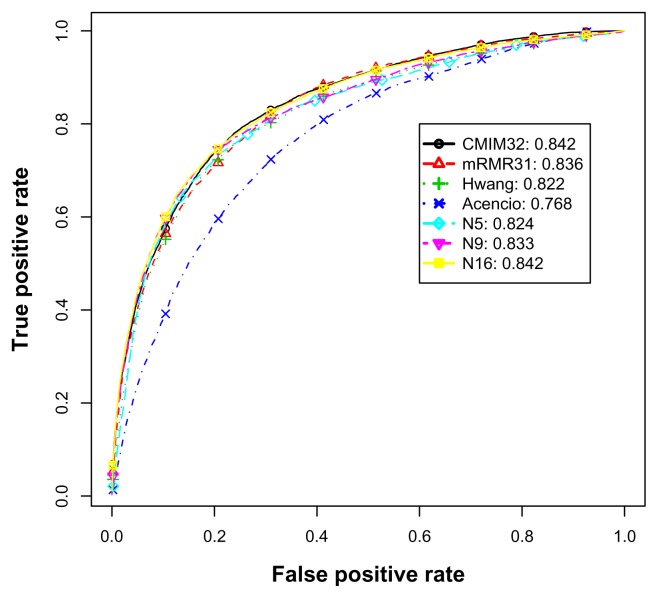
Figure 5 illustrates the average ROC curves and AUCs of various feature subsets for the balanced data experiments. CMIM32 again was the most competent predictor. Additionally, N16 also achieved the same level of AUC. For the feature subsets of sizes ranging from 5 to 18 (not all shown), their true positive rates were either higher or at least close to Hwang’s level. Thus, N5, N6, …, N18 outperformed or performed equally well for various combinations of true and false positive rates in the balanced experiments. Similarly to the imbalanced data set, the more features, the higher the AUC values. However, the improvement in AUC over the feature addition was not as significant as those in the imbalanced experiments. It should be noted that both the ROC curve and AUC of Acencio’s predictor were reproduced by our experiments and thus they were slightly different from the original values reported by Acencio and Lemke.⁵

Figure 5.

The average ROC curves and AUCs for the balanced S. cerevisiae data set.

E. coli

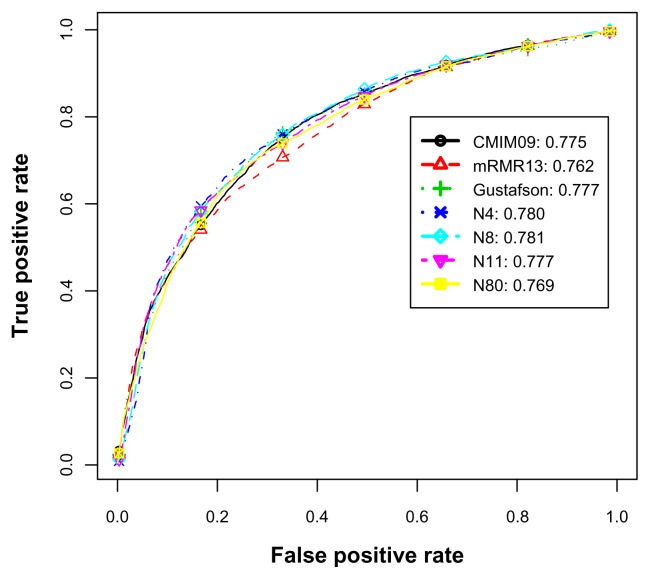
For imbalanced data set, Figure 6 illustrates the average ROC curves and AUCs of various feature subsets. It shows that all curves were similar below the 10% horizontal range. This indicates that there was little difference when the allowable false positive rate was less than 10%. For the horizontal range above 10%, N80 was the highest performer, Gustafson and N11 were secondary, and N4 was the worst. In contrast to the imbalanced data set, for Figure 7 corresponding to the balanced data set, N4 and N8 were the best performers. The remaining predictors showed few differences.

Figure 6.

The average ROC curves and AUCs for the imbalanced E. coli data set.

Figure 7.

The average ROC curves and AUCs for the balanced E. coli data set.

Top percentage analysis

S. cerevisiae

Table 10 shows the average top percentage information for the imbalanced data set. The top θ probability is defined as the ratio of the number of truly predicted essential proteins over the top-ranked θ × 975 proteins, where the total number of true essential proteins is 975. The top θ probability shows the likelihood that the proteins are essential if the user decides to choose a specific number of top-ranked candidates. It is slightly different from precision because the top-ranked candidates (or denominator) are not necessary to be classified as essential. CMIM32, mRMR31 and Hwang’s results again served as benchmarks and they are denoted by star ‘*’ symbols in the table. The minus symbol following each value represents that the value was lower than the benchmark results.

Table 10.

Percentage of essential proteins in the imbalanced S. cerevisiae data.

	Top 5%			Top 10%			Top 15%			Top 20%			Top 25%			Top 30%			Top 50%			Top 75%			Top 100%
CMIM32	0.939*	–	–	0.918*			0.910*			0.892*			0.870*			0.839*			0.743*			0.645*			0.582*
mRMR31	0.955	*	–	0.905–	*	–	0.884–*			0.862–*			0.834–*	–		0.820–*			0.740–*			0.641–*			0.572–*
Hwang(10)	0.959		*	0.918		*	0.871–	–*		0.853–	–*		0.843–		*	0.816–	–*		0.720–	–*		0.637–	–*		0.563–	–*
Acencio(23)	0.800–	–	–	0.741–	–	–	0.693–	–	–	0.661–	–	–	0.646–	–	–	0.625–	–	–	0.578–	–	–	0.519–	–	–	0.457–	–	–
N4	0.980			0.930			0.905–			0.877–			0.865–			0.850			0.727–	–		0.632–	–	–	0.559–	–	–
N5	0.843–	–	–	0.861–	–	–	0.859–	–	–	0.852–	–	–	0.841–		–	0.827–			0.751			0.641–			0.530–	–	–
N6	0.908–	–	–	0.894–	–	–	0.875–	–		0.857–	–		0.850–			0.834–			0.763			0.635–	–	–	0.526–	–	–
N7	0.861–	–	–	0.892–	–	–	0.897–			0.885–			0.854–			0.832–			0.770			0.645–			0.570–	–
N8	0.892–	–	–	0.904–	–	–	0.895–			0.877–			0.868–			0.850			0.751			0.657			0.574–
N9	0.880–	–	–	0.911–		–	0.895–			0.875–			0.860–			0.832–			0.753			0.665			0.585
N10	0.882–	–	–	0.896–	–	–	0.893–			0.882–			0.858–			0.846			0.762			0.665			0.581–
N11	0.900–	–	–	0.900–	–	–	0.888–			0.875–			0.861–			0.856			0.769			0.667			0.580–
N12	0.941	–	–	0.924			0.899–			0.872–			0.866–			0.854			0.776			0.664			0.588
N13	0.941	–	–	0.910–		–	0.886–			0.870–			0.853–			0.840			0.781			0.672			0.578–
N14	0.949	–	–	0.932			0.916			0.897			0.867–			0.845			0.759			0.667			0.587
N15	0.906–	–	–	0.894–	–	–	0.897–			0.884–			0.866–			0.851			0.776			0.672			0.584
N16	0.933–	–	–	0.901–	–	–	0.895–			0.886–			0.864–			0.851			0.771			0.677			0.599
N17	0.943	–	–	0.903–	–	–	0.879–	–		0.871–			0.866–			0.856			0.777			0.679			0.595
N18	0.937–	–	–	0.892–	–	–	0.880–	–		0.870–			0.864–			0.854			0.778			0.683			0.595
N90	0.939	–	–	0.911–		–	0.884–			0.869–			0.856–			0.835–			0.728–	–		0.639–	–		0.572–

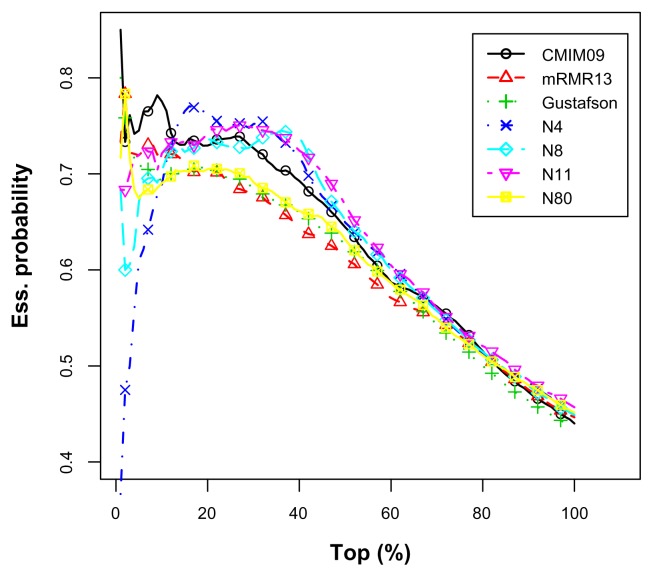
Both mRMR31 and Hwang’s predictor were extremely effective within the 10% range. This indicates that these predictors were quite preferable when the total number of true essential proteins was known and the allowable top-ranked candidates were within 10%. Most of our predictors outperformed them beyond 10%. For CMIM32, our predictors outperformed it beyond 30%. Thus, N14 may be a better choice because it is relatively effective beyond 10%. Figure 8 depicts the average top percentage curves.

Figure 8.

The average top percentage curves for the imbalanced S. cerevisiae data set.

E. coli

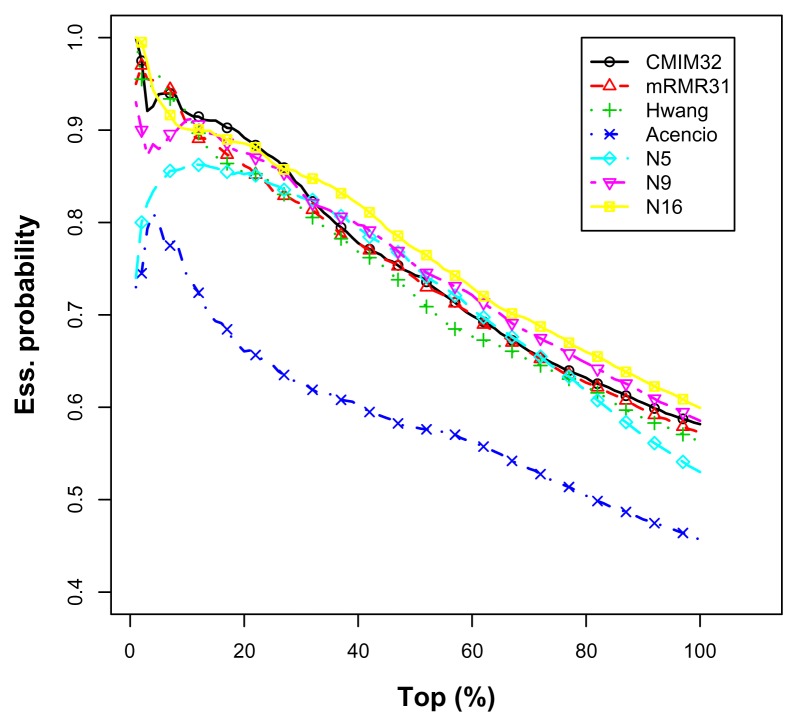
Table 11 shows the average top percentage information for the imbalanced data set. CMIM09, mRMR13, and Gustafson’s results serve as benchmarks. The CMIM09 predictor was the most effective over the entire range. Most of our predictors outperformed these predictors beyond 15%. N9 was the most prominent since it was relatively effective over the entire range. Figure 9 depicts the average top percentage curves.

Table 11.

Percentage of essential proteins in the imbalanced E. coli experiment.

	Top 5%			Top 10%			Top 15%			Top 20%		Top 25%		Top 30%		Top 50%		Top 75%		Top 100%
CMIM09	0.745*			0.775*			0.730*			0.730*		0.737*		0.727*		0.644*		0.542*		0.440*	–
mRMR13	0.719–*			0.725–*			0.714–*			0.701–*	–	0.690–*	–	0.679–*	–	0.614–*	–	0.531–*		0.446*
Gustafson(29)	0.706–	–*		0.692–	–*		0.705–	–*		0.707–	*	0.695–	*	0.685–	*	0.624–	*	0.522–	–*	0.436–	–	*
N4	0.610–	–	–	0.689–	–	–	0.765			0.760		0.749		0.752		0.649		0.534–		0.449
N5	0.655–	–	–	0.705–	–		0.747			0.747		0.745		0.743		0.653		0.535–		0.443	–
N6	0.719–			0.723–	–		0.717–			0.736		0.744		0.748		0.658		0.525–	–	0.435–	–	–
N7	0.568–	–	–	0.700–	–		0.713–	–		0.730		0.748		0.762		0.655		0.540–		0.464
N8	0.671–	–	–	0.703–	–		0.723–			0.736		0.728–		0.731		0.652		0.535–		0.449
N9	0.813			0.785			0.766			0.754		0.734–		0.726–		0.685		0.548		0.459
N10	0.794			0.751–			0.728–			0.732		0.741		0.745		0.668		0.550		0.463
N11	0.719–			0.721–	–		0.734			0.742		0.748		0.748		0.668		0.539–		0.457
N12	0.735–			0.738–			0.745			0.750		0.743		0.740		0.667		0.548		0.458
N13	0.655–	–	–	0.672–	–	–	0.713–	–		0.739		0.736–		0.732		0.668		0.548		0.457
N80	0.674–	–	–	0.690–	–	–	0.703–	–	–	0.705–	–	0.703–		0.691–		0.632–		0.529–	–	0.452

Figure 9.

The average top percentage curves for the imbalanced E. coli data set.

Discussion

By inspecting the S. cerevisiae feature subsets listed in Table 4, we observed that the most prominent features indeed come from diverse sources. This includes sequence, protein, topology and other properties. Among these features, amino acid occurrence I, amino acid occurrence W, bit string of double screening scheme, cytoplasm, endoplasmic reticulum, EI (essentiality index), nucleus, and PR (phyletic retention) were selected more than 10 times. Two among the above features, EI and PR, were included in all feature subsets and thus they are regarded as the most important factors for identifying essential proteins. N9 and N8 were the feature subsets that cover most of the above 8 features. Their prediction capability associated with these two feature subsets outperformed Hwang’s results in all performance measures, except for AUC and the top percentage probability at a very low value. Furthermore, two amino acids, which were relatively easy to extract, were included in these two feature subsets. For predictors that were built by the feature subsets of 10 or more features, they were consistently superior to Hwang’s in nearly all performance measures. Interestingly, mRMR and CMIM selected several sequence-derived features, such as PSSM and amino acid occurrence. It thus seems these features are good for essentiality prediction in terms of relevance and feature independence. By analyzing Tables 6 and 7, we recommend using N16, N9, and N6. N16 performed nearly as well as CMIM32 (or mRMR31) and was more compact in feature size. For N9 and N6, by choosing one additional feature, they were significant higher than N8 and N5 in some performance measures.

For the E. coli features listed in Table 5, the most and second important features were PR (phyletic retention) and open reading frame length. The rest of important features which were selected more than five times included: average PSSM of amino acid C and degree related to integrated functional interactions. N5, N7, N8, and N13 covered most of these features. Among the 43 listed features, 21 sequence-related features, such as amino acid occurrence and average PSSM, were selected. In this data set, we recommend feature subsets of sizes exceeding 11 because of their effectiveness and compactness in feature size.

With experimental results for the two data sets, we conclude that phyletic retention is the most important feature for identifying essential proteins. It is defined as the number of present ortholog organisms. Gustafson et al study²¹ analyzed different organisms to calculate phyletic retention for E. coli and S. cerevisiae data sets. This is sensible because different species may be associated with different organisms. From the biological view, the retention process over long evolutionary periods suggests that some organisms are crucial for certain cell functionality. By inspecting the top 5 occurrences of amino acids in Tables 4 and 5, we find Tryptophan (W) and Glycine (G) were two top-ranking features. Since both these two amino acids are non-polar and hydrophobic, we may hypothesize that either essentiality is related to these physicochemical properties or that the features possessing discrimination information is not captured by other top-ranking features.

In this study, we compiled various interaction information including physical, metabolic, transcriptional regulation, and integrated functional and genomic context interactions. The experimental results revealed that various properties, such as degrees, were more or less identified as important features. This implies that the interaction information, not limited to physical interactions, may also be closely related to essential properties. According to the literature, hubs of the networks, possessing abundance of interaction partners, are important due to the fact that they play central roles in mediating interactions among numerous less-connected proteins. Thus, proteins involved in the complex mediation processes are more likely to be crucial for cellular activity or survival.

For the feature selection proposed in this study, let the size of all available and target selected features be m and t, and the maximal retry times be r. The number of SVM cross-validation times is between 1/2 (m + t + 1) × (m − t) and 1/2 (m + t + 1) × (m − t) × r. It takes approximately 1 minute for the LIBSVM software to perform a 2-fold cross-validation on one Power5+ processor of IBM P595 computer. Assuming m = 90, t = 10 and r = 5, the total running time is between 4,000 and 20,000 minutes. The IBM P595 allows users to manually submit several processes into the computer in order to speed up the execution. For example, we can invoke at most 10 SVM processes simultaneously. Consequently, a maximal 10-time speed-up can be achieved and the total running time can thus be reduced.

If we inspect Tables 4 and 5, we can find that more than one-third of the features were not significantly relevant and thus were not selected. These features are relatively easy to remove during backward feature selection procedure at the beginning stage. According to the authors’ experience, the rounds of retry r are not critical in this stage. With an increasing number of features removed, the required number of retry must be increased as identifying relatively less competent features becomes increasingly difficult. The number of retry r accompanied by the rest of user-specified parameters (such as the minimal improvement ρ et al) was set appropriately to ensure that the feature selection procedure could proceed.

Conclusion and Future Work

In this study, we incorporated several protein properties, including sequence, protein, topology, and other properties. There was a total of 55 groups and 96 features. The features were included in two data sets for experiments: S. cerevisiae and E. coli. We used a modified sequential backward feature selection to identify good feature subsets and used the SVM software tools for classifying essential proteins. In addition, we built several SVM models for both imbalanced and balanced data sets. As our experimental results illustrate, some features were indeed shown to be effective for essentiality prediction. Feature subsets selected by our method were effective in term of feature size and performance. This is because our method took both feature size and performance into consideration and consequently the resultant feature subset was considerably compact. We compared our experimental results by carrying out significance tests for several types of performance measures. Hence, this provides the potential researcher of essential proteins a practical guide to which feature or method is more prominent.

In the imbalanced S. cerevisiae data experiment, our best results for F-measure and MCC were 0.549 and 0.495, respectively, which was associated with the N13 predictor. In contrast, for the same performance measures, we achieved 0.77 and 0.545 in the balanced data experiment, which were associated with the N17 predictor. The experimental results showed that the performance of our models was better than Hwang’s when we selected more than 9 features. If achieving higher accuracy is the main issue, we recommend the N16 model (16 features). When one prefers a compact feature set of small size, we suggest using the N9 model (9 features). We also list important features. These features may be crucial for identifying essential proteins.

For E. coli data set, our best values of F-measure and MCC were 0.421 and 0.407 in the imbalanced experiments. In the balanced experiment, the best values of F-measure and MCC were 0.718 and 0.448, respectively. Both of the best results were associated with the N5 predictor. For the data set, we found that predictors associated with the feature size above 11 were indeed comparable to Gustafsons’.

There several possible methods for further improving the prediction capability. Features related to the protein sequence properties may also be useful for identifying essentiality. Furthermore, since proteins with similar primary structures may possess similar functions, thus the essentiality may be addressed from the sequence motif perspective.³⁴ In addition to the above approaches, performance can be improved by incorporating other tools or constructing hybrid predictors. Among these, the majority vote³⁵ is a strategy for combining classifiers. This method represents the simplest method for categorical data fusion. According to the literature,³⁶ the prerequisite for improvement arises from the fact that each individual classifier must contain distinct information for discrimination. Otherwise, some negative effects may be imposed on the constructed ensemble.

Table 13.

Confidence intervals of performance measures (×100) and informational odds ratios for models produced by the balanced S. cerevisiae data set.

	AUC	Precision	Recall	F1	MCC	IOR
CMIM32	84.2 ± 1.5	77.2 ± 2.2	76.6 ± 2.9	76.9 ± 2.1	54.0 ± 3.9	3.3 ± 0.4
mRMR31	83.6 ± 1.6	76.5 ± 2.4	74.1 ± 3.0	75.2 ± 2.1	51.3 ± 4.1	3.0 ± 0.3
Hwang	82.2 ± 1.7	77.8 ± 2.6	72.0 ± 3.7	74.8 ± 2.3	51.6 ± 3.9	3.0 ± 0.3
Acencio	76.8 ± 2.2	69.6 ± 2.4	73.4 ± 4.0	71.4 ± 2.3	41.4 ± 4.3	2.5 ± 0.3
N4	81.1 ± 1.8	77.7 ± 2.5	71.6 ± 3.6	74.5 ± 2.3	51.2 ± 3.9	3.0 ± 0.3
N5	82.4 ± 1.8	77.8 ± 2.6	73.5 ± 3.5	75.6 ± 2.2	52.7 ± 4.1	3.1 ± 0.3
N6	82.7 ± 1.8	77.8 ± 2.6	73.9 ± 3.6	75.8 ± 2.3	53.0 ± 4.1	3.1 ± 0.3
N7	83.1 ± 1.8	77.9 ± 2.5	73.3 ± 3.5	75.5 ± 2.2	52.6 ± 4.0	3.1 ± 0.3
N8	82.6 ± 1.8	78.6 ± 2.5	72.1 ± 3.5	75.2 ± 2.3	52.7 ± 4.0	3.1 ± 0.3
N9	83.3 ± 1.8	79.1 ± 2.4	73.5 ± 3.4	76.2 ± 2.2	54.1 ± 3.8	3.2 ± 0.3
N10	83.4 ± 1.7	78.9 ± 2.4	73.6 ± 3.3	76.1 ± 2.1	54.0 ± 3.8	3.2 ± 0.3
N11	83.1 ± 1.7	78.4 ± 2.4	73.7 ± 3.5	76.0 ± 2.2	53.5 ± 3.8	3.2 ± 0.3
N12	82.9 ± 1.8	77.9 ± 2.5	73.2 ± 3.1	75.5 ± 2.2	52.6 ± 4.2	3.1 ± 0.3
N13	83.4 ± 1.7	78.8 ± 2.4	73.0 ± 3.5	75.8 ± 2.2	53.5 ± 3.9	3.1 ± 0.3
N14	83.6 ± 1.6	77.7 ± 2.3	74.3 ± 3.4	75.9 ± 2.1	53.0 ± 3.8	3.2 ± 0.3
N15	84.3 ± 1.7	78.4 ± 2.4	74.8 ± 3.3	76.6 ± 2.1	54.2 ± 3.9	3.3 ± 0.4
N16	84.2 ± 1.6	77.7 ± 2.2	75.6 ± 3.1	76.7 ± 2.0	54.0 ± 3.7	3.3 ± 0.4
N17	84.7 ± 1.6	77.8 ± 2.3	76.3 ± 3.0	77.0 ± 2.0	54.5 ± 3.8	3.3 ± 0.4
N18	84.0 ± 1.6	77.9 ± 2.4	74.0 ± 3.3	75.9 ± 2.0	53.1 ± 3.8	3.1 ± 0.3
N90	83.9 ± 1.4	76.0 ± 2.0	75.3 ± 2.7	75.7 ± 1.8	51.6 ± 3.5	3.1 ± 0.3

Table 14.

Confidence intervals of performance measures (×100) and informational odds ratios for models produced by the imbalanced E. coli data set.

	AUC	Precision	Recall	F1	MCC	IOR
CMIM09	70.1 ± 0.9	72.0 ± 1.4	27.1 ± 0.7	39.4 ± 0.9	38.2 ± 0.9	5.2 ± 0.6
mRMR13	71.5 ± 2.4	71.3 ± 5.4	25.0 ± 5.8	37.0 ± 6.8	36.0 ± 5.8	4.7 ± 0.6
Gustafson	71.1 ± 2.3	66.5 ± 4.6	25.5 ± 5.0	36.8 ± 5.2	34.7 ± 4.8	4.9 ± 0.6
N4	69.1 ± 1.8	72.5 ± 1.0	28.0 ± 0.6	40.4 ± 0.7	39.1 ± 0.7	5.5 ± 0.6
N5	69.0 ± 2.0	73.7 ± 1.4	29.5 ± 0.8	42.1 ± 0.9	40.7 ± 1.0	5.7 ± 0.6
N6	70.1 ± 1.7	74.2 ± 1.4	28.7 ± 0.9	41.4 ± 1.1	40.3 ± 1.0	5.7 ± 0.6
N7	71.4 ± 1.4	73.5 ± 1.3	27.5 ± 0.7	40.0 ± 0.9	39.2 ± 0.9	5.5 ± 0.6
N8	70.5 ± 1.3	74.2 ± 1.1	28.8 ± 0.8	41.5 ± 0.9	40.5 ± 0.9	5.7 ± 0.6
N9	70.7 ± 1.5	72.6 ± 1.4	29.3 ± 1.0	41.7 ± 1.2	40.1 ± 1.2	5.6 ± 0.6
N10	71.1 ± 1.5	72.4 ± 1.6	29.4 ± 1.0	41.8 ± 1.1	40.1 ± 1.2	5.6 ± 0.6
N11	71.4 ± 1.4	73.2 ± 1.3	27.8 ± 0.8	40.3 ± 1.0	39.3 ± 1.0	5.5 ± 0.6
N12	71.2 ± 1.4	72.5 ± 1.9	29.2 ± 1.1	41.6 ± 1.2	40.0 ± 1.3	5.6 ± 0.6
N13	71.4 ± 1.3	73.3 ± 1.8	28.7 ± 1.2	41.3 ± 1.4	40.0 ± 1.4	5.6 ± 0.6
N80	71.6 ± 0.9	67.7 ± 2.1	23.7 ± 1.3	35.2 ± 1.6	33.9 ± 1.6	4.9 ± 0.6

Appendix

Feature extraction

• a. Outdegree and in degree related to transcriptional regulation interaction: The feature represents the number of outgoing (or incoming) links to the gene g corresponding to a protein. Links are represented in terms of transcriptional regulation interactions.

• b. Betweenness centrality transcriptional regulation interactions: Let σ_{gi gj} denote the number of shortest paths between g_i and g_j. The value σ_{gi gj} (g) is defined as the number of shortest paths between g_i and g_j passing through g. Paths are represented in terms of transcriptional regulation interactions.

• c. Betweenness centrality related to physical interactions: The value τ_{gi gj} (g) is defined as the number of shortest paths between g_i and g_j passing through g. The definition is similar to the previous one. However, the paths here are represented in terms of protein physical interactions.

• d. Protein properties: Acencio and Lemke⁵ discovered that the integration of topological properties, cellular components, and biological processes possess good capability for predicting essential proteins. Hence, our features also contained cellular components (cytoplasm, endoplasmic reticulum, mitochondrion, nucleus or other localization) and biological processes (cell cycle, metabolic process, signal transduction, transcription, transport or other process).

The above four feature sets were obtained from Acencio and Lemke.⁵

• e. Betweenness centrality related to integrated functional, PI and GC network: The values are defined identically as those mentioned above while the paths here are represented in terms of integrated functional, PI and GC network interactions.

• f. Degree related to integrated functional, PI and GC network: The values were defined identically to those mentioned above, while the paths here are represented in terms of integrated functional, PI, and GC network interactions.

For the above two feature sets, we first collected network information from Hu et al²² and then conducted calculations using iGraph software.³⁷

• g. Maximum neighborhood component and density of maximum neighborhood component: The maximum neighborhood component (MNC) and density of maximum neighborhood component (DMNC) properties were proposed by Lin et al²⁶ and Chin.⁴ For a protein i, let N(i) be the set of neighbors of i. The MNC of i is the connected component of N(i) with maximum size, and it is denoted as M N(i).

  For a protein i, the number of proteins and the number of edges in M N (i) are denoted as n_i and d_i, respectively. DMNC of i is d_i/n_i^α for some 1 ≤ α ≤ 2. In their system, they set α to 1.7.

• h. Sequence features: We used ten feature sets from Lin et al.²⁰ Let L be the protein length, F_i be the occurrence number of amino acid i in the protein, H (i) be the hydrophobic coefficient³⁸ of amino acid i, P_i,j be the position of the jth occurrence of amino acid i, A(j) be the amino acid of position j and S_m,n be the score of row m and column n in PSSM.³⁹

  The sequence features are listed as follows.

  1. Protein length: L

  2. Cysteine count: F_C

  3. Amino acid occurrence: The composition of amino acid i is F_i/L, where 1 ≤ i ≤ 20.

  4. Average cysteine position: ${\sum }_{j=1}^{F_C}{P}_{C,j}/F_C$

  5. Average distance of every two cysteines: $\frac{{\sum }_{x=1}^{F_C}{\sum }_{y=1}^{F_C}|P_{C,x}-P_{C,y}|}{L\times F_C}$

  6. Cysteine odd-even index: F_C mod 2.

  7. Average hydrophobicity: ${\sum }_{i=1}^{20}{F}_i\times H(i)/L$

  8. Average hydrophobicity around cysteine: The kth values of average hydrophobicity around all cysteines were defined as ${\sum }_{j=1}^{F_C}H\left(A(P_{C,j}+k)\right)/F_C$. Here we set k = −2, −1, +1, +2.

  9. Cysteine position distribution: For 1 ≤ d ≤ ρ, the dth cysteine position distribution was

     $$\frac{\left|\left\{{\alpha }_j|{\alpha }_j=\frac{P_{C,j}}{L},\frac{d-1}{\rho }<{\alpha }_j\le \frac{d}{\rho },1\le j\le F_C\right\}\right|}{F_c}$$

     We set ρ = 5

  10. Average PSSM of amino acid: The average PSSM of residue i is ${\sum }_{m=1}^L{S}_{m,i}/L$.

• i. Phyletic retention: Gustafson et al²¹ discovered that the essential proteins are generally more conserved than nonessential proteins. Phyletic retention of protein i is the number of organisms in which an ortholog is present. The ortholog of each protein was obtained from Hwang et al.⁷

• j. Essential index:⁷ Essential index measures the ratio of essential proteins in the neighbors N(i) of node i. Essential index of node i is defined as p(i)/d_i, where p(i) is the number of essential proteins in N(i) and d_i is the degree of node i.

• k. Clique level:⁷ The clique level of protein i is defined as the maximal clique containing i. Here, only cliques with sizes between 3 and 10 were taken into consideration.

• l. Number of paralagous genes: It is shown that genes are more likely to be essential if there no duplicate existed in the same genome.²¹ This feature is defined as the number of genes that are present in the same genome. In addition, their BLASTP E-values must be less than 10⁻²⁰ and the ratios of the larger gene to the smaller do not exceed 1.33.

• m. Open reading frame length: Gustafson et al²¹ observed that ancestral genes are more likely to be essential and that proteins generally become larger throughout evolution. Consequently, The open reading frame length may indicate essentiality.

Confidence intervals of performance measures and informational odds ratios

All performance measures were multiplied by 100. The confidence intervals were set at 95%. We used the informational odds ratios (IOR)³² to represent the association between the essentiality and predictions. IOR measures how much more likely a protein is to be essential when one learning machine outputs essentiality rather than non-essentiality. A value of 1.0 indicates no association between the essentiality and predictions produced by learning machines. All confidence intervals of performance measures and informational odds ratios corresponding to each prediction models are shown in Tables 12–15.

Table 12.

Confidence intervals of performance measures (×100) and informational odds ratios for models produced by the imbalanced S. cerevisiae data set.

	AUC	Precision	Recall	F1	MCC	IOR
CMIM32	82.5 ± 1.2	74.4 ± 3.1	36.9 ± 4.5	49.3 ± 3.8	45.0 ± 3.6	5.2 ± 0.5
mRMR31	82.1 ± 1.6	73.8 ± 3.2	37.2 ± 4.3	49.5 ± 3.6	44.9 ± 3.4	5.2 ± 0.5
Hwang	77.5 ± 2.2	74.3 ± 3.7	34.3 ± 4.3	46.9 ± 4.0	43.2 ± 3.6	5.1 ± 0.4
Acencio	70.7 ± 3.4	67.5 ± 6.3	12.1 ± 5.5	20.4 ± 7.6	22.8 ± 6.0	3.7 ± 0.4
N4	74.4 ± 2.7	78.2 ± 3.7	32.7 ± 4.1	46.1 ± 4.1	43.9 ± 3.5	5.3 ± 0.4
N5	72.7 ± 3.6	74.1 ± 4.1	38.7 ± 4.7	50.9 ± 4.1	46.1 ± 3.8	5.3 ± 0.5
N6	73.0 ± 3.2	75.2 ± 4.2	39.5 ± 4.4	51.8 ± 3.8	47.2 ± 3.6	5.5 ± 0.5
N7	76.1 ± 2.4	76.7 ± 3.7	38.6 ± 4.4	51.3 ± 3.9	47.3 ± 3.6	5.5 ± 0.5
N8	77.2 ± 2.4	75.5 ± 3.4	37.1 ± 4.9	49.8 ± 4.3	45.7 ± 3.9	5.3 ± 0.5
N9	78.2 ± 2.4	74.9 ± 3.4	38.2 ± 4.5	50.6 ± 3.9	46.2 ± 3.6	5.4 ± 0.5
N10	78.1 ± 2.2	75.1 ± 3.5	39.9 ± 4.1	52.1 ± 3.6	47.4 ± 3.5	5.5 ± 0.5
N11	78.6 ± 2.1	75.2 ± 3.2	40.2 ± 4.2	52.4 ± 3.6	47.6 ± 3.4	5.5 ± 0.5
N12	79.8 ± 2.0	75.9 ± 3.2	40.9 ± 4.2	53.2 ± 3.6	48.5 ± 3.4	5.7 ± 0.5
N13	78.9 ± 1.9	74.8 ± 3.2	43.3 ± 4.3	54.9 ± 3.4	49.5 ± 3.4	5.8 ± 0.5
N14	80.2 ± 1.8	74.9 ± 3.2	39.7 ± 4.3	51.9 ± 3.5	47.1 ± 3.4	5.5 ± 0.5
N15	80.1 ± 1.9	76.3 ± 3.3	40.6 ± 4.2	53.0 ± 3.5	48.5 ± 3.5	5.7 ± 0.5
N16	81.4 ± 1.7	76.2 ± 3.2	40.1 ± 4.6	52.5 ± 3.8	48.0 ± 3.6	5.6 ± 0.5
N17	81.4 ± 1.7	76.1 ± 3.3	40.7 ± 4.5	53.0 ± 3.8	48.4 ± 3.6	5.7 ± 0.5
N18	81.1 ± 1.8	75.1 ± 3.2	41.1 ± 4.3	53.1 ± 3.6	48.2 ± 3.5	5.6 ± 0.5
N90	82.9 ± 1.0	73.8 ± 2.8	35.5 ± 4.5	47.9 ± 3.6	43.8 ± 3.4	5.1 ± 0.4

Table 15.

Confidence intervals of performance measures (×100) and informational odds ratios for models produced by balanced E. coli data set.

	AUC	Precision	Recall	F1	MCC	IOR
CMIM09	76.7 ± 1.7	72.0 ± 2.4	70.0 ± 3.7	71.0 ± 2.2	42.1 ± 4.0	2.4 ± 0.3
mRMR13	76.2 ± 2.0	72.8 ± 3.1	65.4 ± 6.4	68.9 ± 3.3	39.6 ± 3.9	2.2 ± 0.2
Gustafson	77.7 ± 2.6	72.2 ± 3.3	71.5 ± 4.0	71.9 ± 2.8	44.0 ± 5.5	2.6 ± 0.3
N4	78.0 ± 1.6	73.3 ± 2.5	70.1 ± 2.7	71.7 ± 1.9	44.6 ± 3.8	2.6 ± 0.3
N5	77.9 ± 1.7	73.0 ± 2.5	70.6 ± 2.8	71.8 ± 1.8	44.5 ± 3.8	2.6 ± 0.3
N6	76.2 ± 1.7	73.5 ± 2.6	66.3 ± 4.3	69.6 ± 2.6	42.5 ± 4.1	2.4 ± 0.3
N7	78.3 ± 1.7	73.7 ± 2.5	69.6 ± 2.7	71.6 ± 1.8	44.8 ± 3.6	2.6 ± 0.3
N8	78.1 ± 1.7	72.3 ± 2.3	71.1 ± 3.3	71.7 ± 2.1	43.9 ± 3.8	2.5 ± 0.3
N9	78.2 ± 1.6	71.5 ± 2.2	70.3 ± 4.1	70.9 ± 2.3	42.3 ± 3.8	2.4 ± 0.3
N10	78.1 ± 1.6	72.5 ± 2.4	70.2 ± 3.3	71.3 ± 2.1	43.6 ± 3.9	2.5 ± 0.3
N11	77.7 ± 1.7	71.9 ± 2.2	70.0 ± 3.3	70.9 ± 2.0	42.6 ± 3.6	2.5 ± 0.3
N12	77.6 ± 1.9	71.5 ± 2.3	69.5 ± 4.5	70.5 ± 2.5	41.8 ± 4.0	2.4 ± 0.3
N13	77.6 ± 1.7	73.1 ± 2.4	69.5 ± 3.0	71.2 ± 2.1	43.9 ± 3.9	2.5 ± 0.3
N80	76.9 ± 1.8	71.1 ± 2.4	71.5 ± 2.4	71.3 ± 1.8	42.4 ± 3.8	2.5 ± 0.3

Comparison with other feature selection methods

We first introduced two feature selection methods that served as benchmarks, mRMR¹³ and CMIM,¹⁴ both of which are theoretical methods. Next, we compared them with our feature selection method when the feature subsets of equal size were selected.

Unlike other methods that select top-ranking features based on F-score or mutual information without considering relationships among features, mRMR accommodates both feature relevance with respect to class label and dependency among selected features. The strategy combines both the maximal relevance and the minimal redundancy criteria. In order to take the above two criteria into consideration and to avoid an exhaustive search, mRMR adopts an incremental search approach. That is, the rth selected feature should satisfy

$$X_r=\underset{X_j\in X-X_{r-1}}{\text{arg\hspace{0.17em}max}}\left\{I(X_j,Y)-\frac{1}{r-1}\sum _{X_i\in X_{r-1}}I(X_j,X_i)\right\}$$ (1)

where X is the full feature set. X_i is a feature within X_r−1 and r − 1 is the number of selected features contained in X_r−1. X_j is any feature that is not yet selected. I (X_j, Y) is mutual information and it quantifies the dependence (or relevance) between the feature X_j and class label Y. This means that the rth selected feature should be as relevant to the class label as possible while possesses least dependency averagely to the selected features.

For CMIM, a feature X_j is good if I (Y, X_j|X_i) is large for every selected feature X_i. I (Y, X_j|X_i) is conditional mutual information and it quantifies discrepancy between features X_j and X_i for given the class label Y. Consequently, the feature selection procedure was also carried out in an incremental manner as follows:

$$\nu (1)=\mathit{arg}\hspace{0.17em}\underset{X_j}{\text{max}}\hspace{0.17em}I(X_j,Y)$$ (2)

$$\nu (r)=\mathit{arg}\hspace{0.17em}\underset{X_j}{\text{max}}\hspace{0.17em}\left\{\underset{k\le r-1}{\text{min}}I(Y,X_j\mid X_{\nu (k)})\right\}.$$ (3)

where v(k) denotes the kth selected feature.

In the following paragraph, we compare our method with the above two feature selection methods when the feature subsets of equal size were selected. We first ran the SVM software with Hwang’s or Gustafson feature sets and tune the SVM parameters to achieve the highest average performances. To fairly compare the methods given feature subsets with same sizes obtained by our methods, mRMR and CMIM, we used the same SVM software and adjust the cost parameters in order to achieve similar levels of precision. For S. cerevisiae and E. coli data set, the feature numbers k are 4 ≤ k ≤ 18 and 4 ≤ k ≤13, respectively, to be compliant with those in Section V.

For the S. cerevisiae data set in the imbalanced experiment, Tables 16 and 17 show the performance comparison of our method versus mRMR and CMIM. Our method performed significantly better when the size of a feature subset exceeded 7. For the balanced experiment, as illustrated in Tables 18 and 19, our method was significantly better only when the number of selected features exceeded 16.

Table 16.

Performance comparison of our method vs. mRMR for the imbalanced S. cerevisiae data set with the same sizes of feature subsets, where the > symbol represents that the values are significantly higher.

	AUC		Precision		Recall		F-measure		MCC
N4	0.744	0.762	0.782	0.756	0.327	0.331	0.461	0.461	0.439	0.430
N5	0.727	0.718	0.741	0.740	0.387	0.359	0.509	0.484	0.461	0.442
N6	0.730	0.753	0.752	0.753	0.395 >	0.333	0.518 >	0.462	0.472 >	0.430
N7	0.761	0.763	0.767	0.761	0.386 >	0.330	0.513 >	0.460	0.473 >	0.431
N8	0.772 >	0.771	0.755	0.757	0.371 >	0.326	0.498 >	0.456	0.457 >	0.427
N9	0.782	0.776	0.749	0.749	0.382 >	0.341	0.506 >	0.469	0.462 >	0.434
N10	0.781 >	0.778	0.751	0.752	0.399 >	0.340	0.521 >	0.469	0.474 >	0.434
N11	0.786 >	0.774	0.752	0.750	0.402 >	0.341	0.524 >	0.469	0.476 >	0.434
N12	0.798 >	0.781	0.759	0.757	0.409 >	0.334	0.532 >	0.463	0.485 >	0.432
N13	0.789 >	0.774	0.748	0.746	0.433 >	0.342	0.549 >	0.469	0.495 >	0.432
N14	0.802 >	0.775	0.749	0.750	0.397 >	0.340	0.519 >	0.468	0.471 >	0.433
N15	0.801 >	0.798	0.763	0.764	0.406 >	0.318	0.530 >	0.449	0.485 >	0.424
N16	0.814 >	0.799	0.762	0.762	0.401 >	0.318	0.525 >	0.449	0.480 >	0.423
N17	0.814 >	0.799	0.761	0.759	0.407 >	0.326	0.530 >	0.456	0.484 >	0.427
N18	0.811 >	0.797	0.751	0.749	0.411 >	0.342	0.531 >	0.469	0.482 >	0.434

Table 17.

Performance comparison of our new method vs. CMIM for the imbalanced S. cerevisiae data set when identical number of features are selected.

	AUC		Precision		Recall		F1		MCC
N4	0.744	0.761	0.782	0.762	0.327	0.344	0.461	0.474	0.439	0.442
N5	0.727	0.735	0.741	0.738	0.387	0.371	0.509	0.494	0.461	0.449
N6	0.730	0.757	0.752	0.749	0.395	0.359	0.518	0.485	0.472	0.446
N7	0.761	0.779	0.767	0.763	0.386 >	0.339	0.513 >	0.470	0.473 >	0.439
N8	0.772	0.779	0.755	0.754	0.371 >	0.350	0.498 >	0.478	0.457 >	0.442
N9	0.782	0.776	0.749	0.750	0.382 >	0.357	0.506 >	0.483	0.462 >	0.445
N10	0.781	0.782	0.751	0.751	0.399 >	0.353	0.521 >	0.480	0.474 >	0.443
N11	0.786	0.786	0.752	0.752	0.402 >	0.363	0.524 >	0.490	0.476 >	0.450
N12	0.798	0.799	0.759	0.758	0.409 >	0.354	0.532 >	0.483	0.485 >	0.447
N13	0.789	0.797	0.748	0.750	0.433 >	0.360	0.549 >	0.487	0.495 >	0.447
N14	0.802 >	0.801	0.749	0.749	0.397 >	0.348	0.519 >	0.475	0.471 >	0.438
N15	0.801 >	0.797	0.763	0.760	0.406 >	0.330	0.530 >	0.460	0.485 >	0.430
N16	0.814 >	0.796	0.762	0.759	0.401 >	0.338	0.525 >	0.468	0.480 >	0.436
N17	0.814 >	0.795	0.761	0.756	0.407 >	0.339	0.530 >	0.469	0.484 >	0.435
N18	0.811	0.799	0.751	0.756	0.411 >	0.338	0.531 >	0.467	0.482 >	0.435

Table 18.

Performance comparison of our method vs. mRMR for the balanced S. cerevisiae data set with the same sizes of feature subsets, where the > symbol indicates that the values are significantly higher.

	AUC		Precision		Recall		F-measure		MCC
N4	0.811	0.815	0.777	0.770	0.716	0.725	0.745	0.747	0.512	0.510
N5	0.824	0.818	0.778	0.771	0.735	0.722	0.756	0.745	0.527	0.508
N6	0.827	0.814	0.778	0.775	0.739	0.709	0.758	0.740	0.530	0.504
N7	0.831	0.824	0.779	0.779	0.733	0.718	0.755	0.747	0.526	0.516
N8	0.826	0.827	0.786	0.781	0.721	0.721	0.752	0.750	0.527	0.521
N9	0.833	0.834	0.791	0.783	0.735	0.734	0.762	0.758	0.541	0.531
N10	0.834	0.835	0.789	0.783	0.736	0.733	0.761	0.757	0.540	0.531
N11	0.831	0.834	0.784	0.780	0.737	0.730	0.760	0.754	0.535	0.525
N12	0.829	0.834	0.779	0.778	0.732	0.734	0.755	0.755	0.526 >	0.525
N13	0.834	0.834	0.788	0.779	0.730	0.732	0.758	0.754	0.535	0.525
N14	0.836	0.832	0.777	0.777	0.743	0.731	0.759	0.753	0.530	0.522
N15	0.843	0.835	0.784	0.778	0.748	0.734	0.766	0.756	0.542	0.526
N16	0.842 >	0.836	0.777	0.777	0.756 >	0.735	0.767 >	0.755	0.540 >	0.525
N17	0.847 >	0.834	0.778	0.777	0.763	0.733	0.770 >	0.754	0.545 >	0.523
N18	0.840	0.835	0.779	0.778	0.740	0.735	0.759	0.756	0.531	0.526

Table 19.

Performance comparison of our method vs. CMIM for the balanced S. cerevisiae data set when identical number of features are selected.

	AUC		Precision		Recall		F1		MCC
N4	0.811	0.813	0.777	0.777	0.716	0.724	0.745	0.749	0.512	0.517
N5	0.824	0.817	0.778	0.775	0.735	0.740	0.756	0.757	0.527	0.526
N6	0.827	0.821	0.778	0.777	0.739	0.742	0.758	0.759	0.530	0.529
N7	0.831	0.830	0.779	0.772	0.733	0.744	0.755	0.758	0.526	0.524
N8	0.826	0.833	0.786	0.776	0.721	0.738	0.752	0.756	0.527	0.525
N9	0.833	0.834	0.791	0.775	0.735	0.740	0.762	0.757	0.541	0.526
N10	0.834	0.835	0.789	0.776	0.736	0.739	0.761	0.757	0.540	0.527
N11	0.831	0.836	0.784	0.778	0.737	0.739	0.760	0.758	0.535	0.528
N12	0.829	0.838	0.779	0.779	0.732	0.742	0.755	0.760	0.526	0.532
N13	0.834	0.837	0.788	0.778	0.730	0.741	0.758	0.759	0.535	0.530
N14	0.836	0.836	0.777	0.777	0.743	0.743	0.759	0.759	0.530	0.530
N15	0.843	0.836	0.784	0.777	0.748	0.739	0.766	0.758	0.542	0.528
N16	0.842 >	0.837	0.777	0.776	0.756	0.741	0.767 >	0.758	0.540 >	0.528
N17	0.847 >	0.838	0.778	0.777	0.763 >	0.744	0.770 >	0.760	0.545 >	0.531
N18	0.840	0.837	0.779	0.778	0.740	0.746	0.759	0.762	0.531	0.533

For the E. coli data set in the imbalanced experiment, Tables 20 and 21 show the performance comparison of our method versus mRMR and CMIM with configurations similar to the S. cerevisiae data set. Our method performed significantly better when the size of a feature subset exceeded 9. For the balanced experiment, as illustrated in Table 22 and 23, our method performed significantly better than mRMR when the numbers of selected features exceeded 7. The experimental results showed almost no difference between our method and CMIM except for N6 AUC.

Table 20.

Performance comparison of our method vs. mRMR for the imbalanced E. coli data set when identical numbers of features are selected.

	AUC		Precision		Recall		F1		MCC
N4	0.691	0.651	0.725	0.678	0.280	0.269	0.404	0.385	0.391	0.363
N5	0.690	0.675	0.737	0.687	0.295	0.254	0.421	0.371	0.407	0.356
N6	0.701	0.681	0.742	0.708	0.287	0.220	0.414	0.336	0.403	0.338
N7	0.714	0.686	0.735	0.712	0.275	0.212	0.400	0.326	0.392	0.333
N8	0.705	0.692	0.742	0.713	0.288	0.209	0.415	0.323	0.405	0.330
N9	0.707	0.692	0.726	0.713	0.293 >	0.199	0.417 >	0.312	0.401	0.322
N10	0.711	0.697	0.724	0.703	0.294 >	0.193	0.418 >	0.302	0.401	0.313
N11	0.714 <	0.702	0.732	0.697	0.278 >	0.187	0.403	0.295	0.393	0.306
N12	0.712 <	0.704	0.725	0.683	0.292	0.192	0.416	0.300	0.400	0.305
N13	0.714 <	0.715	0.733	0.713	0.287	0.250	0.413	0.370	0.400	0.360

Table 21.

Performance comparison of our method vs. CMIM for the imbalanced E. coli data set when identical numbers of features are selected.

	AUC		Precision		Recall		F1		MCC
N4	0.691 >	0.663	0.725	0.717	0.280	0.271	0.404	0.393	0.391	0.381
N5	0.690	0.686	0.737	0.710	0.295 >	0.264	0.421 >	0.385	0.407 >	0.373
N6	0.701	0.697	0.742	0.715	0.287 >	0.265	0.414 >	0.387	0.403 >	0.376
N7	0.714	0.693	0.735	0.711	0.275 >	0.261	0.400 >	0.382	0.392 >	0.371
N8	0.705	0.690	0.742	0.709	0.288 >	0.254	0.415 >	0.373	0.405 >	0.364
N9	0.707	0.701	0.726	0.720	0.293 >	0.271	0.417 >	0.394	0.401 >	0.382
N10	0.711	0.702	0.724	0.692	0.294 >	0.248	0.418 >	0.364	0.401 >	0.353
N11	0.714	0.698	0.732	0.690	0.278 >	0.247	0.403 >	0.363	0.393 >	0.351
N12	0.712	0.690	0.725	0.683	0.292 >	0.239	0.416 >	0.353	0.400 >	0.342
N13	0.714	0.688	0.733	0.678	0.287 >	0.236	0.413 >	0.349	0.400 >	0.337

Table 22.

Performance comparison of our method vs. mRMR for the balanced E. coli data set when identical numbers of features are selected.

	AUC		Precision		Recall		F1		MCC
N4	0.780 >	0.773	0.733	0.726	0.701 >	0.651	0.717 >	0.686	0.446 >	0.407
N5	0.779	0.772	0.730	0.720	0.706 >	0.654	0.718 >	0.684	0.445 >	0.401
N6	0.762	0.771	0.735	0.717	0.663	0.649	0.696	0.680	0.425	0.394
N7	0.783 >	0.768	0.737	0.716	0.696	0.649	0.716 >	0.680	0.448 >	0.394
N8	0.781 >	0.764	0.723	0.715	0.711 >	0.641	0.717 >	0.675	0.439 >	0.387
N9	0.782 >	0.764	0.715	0.713	0.703	0.643	0.709 >	0.675	0.423 >	0.386
N10	0.781 >	0.765	0.725	0.716	0.702 >	0.636	0.713 >	0.673	0.436 >	0.386
N11	0.777 >	0.766	0.719	0.720	0.700	0.643	0.709 >	0.678	0.426	0.394
N12	0.776	0.765	0.715	0.714	0.695	0.643	0.705	0.676	0.418	0.388
N13	0.776 >	0.762	0.731	0.728	0.695 >	0.654	0.712 >	0.689	0.439 >	0.396

Table 23.

Performance comparison of our method vs. CMIM for the balanced E. coli data set when identical numbers of features are selected.

	AUC		Precision		Recall		F1		MCC
N4	0.780	0.769	0.733	0.719	0.701	0.696	0.717	0.707	0.446	0.424
N5	0.779	0.771	0.730	0.715	0.706	0.696	0.718	0.705	0.445	0.419
N6	0.762 <	0.771	0.735	0.716	0.663	0.684	0.696	0.699	0.425	0.413
N7	0.783	0.769	0.737	0.711	0.696	0.696	0.716	0.703	0.448	0.413
N8	0.781	0.767	0.723	0.709	0.711	0.697	0.717	0.703	0.439	0.412
N9	0.782	0.767	0.715	0.720	0.703	0.700	0.709	0.710	0.423	0.421
N10	0.781	0.767	0.725	0.705	0.702	0.702	0.713	0.704	0.436	0.409
N11	0.777	0.765	0.719	0.706	0.700	0.700	0.709	0.703	0.426	0.408
N12	0.776	0.764	0.715	0.703	0.695	0.698	0.705	0.700	0.418	0.404
N13	0.776	0.765	0.731	0.704	0.695	0.700	0.712	0.702	0.439	0.406

For methods such as mRMR and CMIM, both relevance and information redundancy are taken into consideration. Therefore, the obtained feature subsets were quite compact as well as effective. However, the relevance may only be appropriate for some performance measures, such as classification accuracy or precision. Our method took both the performance and feature size into consideration. Consequently, the resultant feature subsets were more effective in some other performance measures for given equal number of features and precision values.