Specific evidence of low-dimensional continuous attractor dynamics in grid cells

Abstract

We examine simultaneously recorded spikes from multiple grid cells, to elucidate mechanisms underlying their activity. We demonstrate that grid cell population activity, among cells with similar spatial periods, is confined to lie close to a 2-dimensional manifold: grid cells differ only along two dimensions of their responses and are otherwise nearly identical. The relationships between cell pairs are conserved despite extensive deformations of single-neuron responses. Results from novel environments suggest such structure is not inherited from hippocampal or external sensory inputs. Across conditions, cell-cell relationships are better conserved than the responses of single cells. Finally, the system is continually subject to perturbations that were the 2-d manifold not attractive, would drive the system to inhabit a different region of state-space than observed. Together, these findings have strong implications for theories of grid cell activity, and provide compelling support for the general hypothesis that the brain computes using low-dimensional continuous attractors.

Introduction

A set of N uncoupled spiking neurons, each with dynamic range Q, supply a vast representational space (volume ~Q^N), (Fig. 1a, top). However, the representation has poor resistance to noise: each state is independent and if changed to another, there is no restoring dynamics to correct the state. Even in the absence of noise, the states persist only for the time-constant of single neurons.

Figure 1.

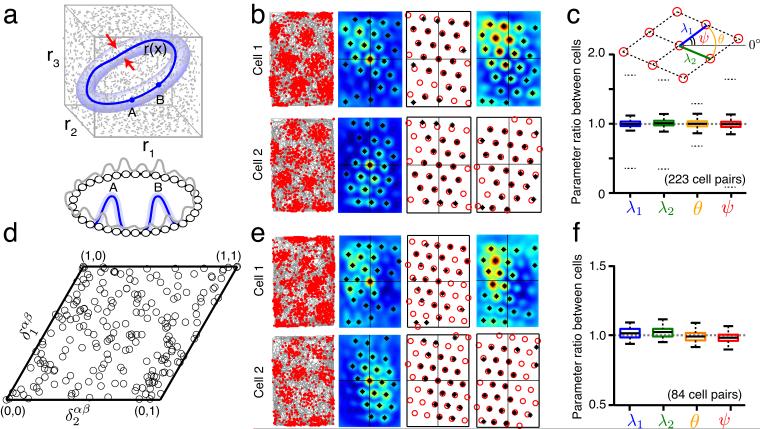
Spatial grid parameters other than phase are identical across cells recorded on the same or nearby tetrodes; cell-cell relationships are stable over time. (a) Top (state space): The state of N independent neurons, each described by a firing rate r_i in [0, r_max] may lie anywhere in an N -dimensional cube of side length r_max□ (shown for N = 3 neurons). Appropriate coupling between the neurons can shrink the allowed states to a low-dimensional attractor (dark blue). All other states are transient, rapidly decaying back to the attractor, and are thus rarely seen. States very close to the attractor (light blue), through transient, may be observed if perturbations frequently drive the system into those states. Bottom: An example network of N neurons (small circles) with 1-d continuous attractor dynamics. Local excitatory and global inhibitory connections (not shown) between all neurons stabilize population states that are local activity bumps (e.g. blue bump A or B; gray: transient/unstable activity profiles). An activity bump is a single point on the continuous attractor (top) of all possible translations of the bump. If points on the attractor are identified with values of some circular variable, then all neural tuning curves for that variable will be identical, except for a phase shift (translation). (b) Column one: Recorded spikes (red dots) of two simultaneously recorded cells as a function of space (rat trajectory: gray lines). Column two: Autocorrelograms of the smoothed spatial response (peaks identified by black asterisks). Column three: A template lattice (red circles) is fit to all the peaks of the autocorrelogram. Parameters of the template (see c, inset) include the two primary axis lengths (λ₁,λ₂) and two angles (θ,ψ). Column four: Crosscorrelogram between the two cells (top), and the corresponding template fit (bottom). (c) Box plot of the ratio of each lattice parameter across 223 cell pairs (e.g., θ” (cell ” i)/θ” (cell ” j)” where ” i > j ) (median ratio: center line in box; interquartile ranges: box; lowest and highest values within 1.5 × of interquartile range: outer horizontal lines; 95% confidence interval based on 223 randomly chosen pairs not recorded simultaneously: dotted outer horizontal lines). (d) The distribution of relative phases (black circles) between all cell pairs, plotted within a canonical unit cell of the grid lattice. (e) Discharge maps (as in b) of the same cell pair, recorded again after an interval of > 60 minutes. (f) Box plot of parameter ratios (as in c) from this later trial, for the subset of cell pairs from c that were also recorded in this trial (N = 84 cell pairs).

Coupling between neurons generally disallows many states, shrinking the representational space (Fig. 1a, top and bottom). An advantage of coupling is that it can, in special cases, produce stable fixed points (attractors) of the network dynamics that allow the network to hold a state after inputs are removed, for far longer than the single-neuron time-constant. Moreover, if noise is present in the system, it may perturb the system off the attractor, but the perturbations are transient and automatically corrected as the system rapidly flows back toward the attractor (Fig. 1a, top). Discrete or point attractors, as in Hopfield networks, may be used to represent discrete items¹. In many cases, the brain must represent continuous variables. In these cases, the value of the variable could be represented as a point on a continuous manifold of stable fixed points, of the same dimensionality D as the variable^2–5. This manifold is called a low-dimensional continuous attractor, if its dimensionality is much smaller than the number of neurons in the network (D « N). In these ways, attractors enable robust representation and memory, albeit at the cost of diminished representational space.

Low-dimensional continuous attractor dynamics have been widely hypothesized to underlie the stable tuning curves of population codes^2,6, motor control^3,7, neural integration^3,4,8–15, and parametric working memory^16,17. The predicted signatures of low-dimensional continuous attractors in the neural context are systematic differences in neural responses along the attractor manifold (e.g. preferred angles that vary along a continuum for a 1-d ring attractor, Fig. 1a, bottom) but conformity and stability otherwise (e.g. tuning curves generated by pulling a rigid activity bump across the 1-d ring attractor). Critically, the mapping of states on the attractor to specific values of the represented variable may vary based on changing associations between the network and the external world (e.g. rotation of the network states relative to the world), but relationships between cells (e.g., whether they are in-phase or counter-phase or quadrature-phase in their relative activity patterns), must remain absolutely stable^3,4,12,15. In other words, the responses of cells – when plotted against the external represented quantity – may change substantially, but pairwise relationships between cells should not. Despite these predictions, and beautiful empirical results^10,11,18,19, definitive validation of the low-dimensional continuous attractor hypothesis has been somewhat elusive: In most cases, partly because of the difficulty of inducing sufficient change or perturbation in the neural responses and partly because quantitative analyses on simultaneously recorded neural pairs have not been conducted, it has been unclear whether the dynamics are truly low-dimensional, what the dimension is, or where the dynamics originates^10,18,19.

Mammalian grid cells²⁰, each of which fires at the vertices of a regular spatial grid as the animal moves through its environment, are hypothesized^{12–15,20–23} to compute ongoing location estimates through integration of self-motion cues, based on the theoretical argument that their responses constitute a relatively context-independent code for spatial displacements. Across different familiar environments, the firing field locations in a grid cell change only through global phase shifts and rotations^20,24, in contrast with place cells, which change in more elaborate ways, by gains or losses and shifts in subsets of their place fields^25–29. The notable regularity and stability of a grid cell’s response hints that the population might be well-described by relatively few parameters, a signature of an underlying low-dimensional dynamical system.

On the other hand, spatially periodic firing in grid cells is neither necessary nor sufficient for inferring low-dimensional population dynamics: It is theoretically possible for the population dynamics to be low-dimensional and periodic without spatially regular firing in individual cells, because of poor velocity integration¹⁵. Conversely, if the N cells in a single population have periodic spatial responses, but each displays independent shifts (relative to the other cells) of its spatial phase across environments, the dimensionality of the population response would be high, or ~N. Finally, experiments that involve resizing of a familiar environment, or exploration in novel environments, reveal that grid cell spatial responses stretch along one or both dimensions^30–32, a malleable response that is possibly consistent with higher-dimensional dynamics.

Here we examine spikes from simultaneously recorded grid cell pairs, in experiments where the single-cell responses undergo significant change, and where external inputs do not provide reliable spatial cues, to rigorously determine across conditions the dimensionality of the population response for each grid cell network or module (discrete networks or modules, consisting of local groups of cells with a common grid period and orientation, were predicted to exist through modeling^12,15,22,33 and experimentally validated^30,32), and thus probe for evidence of low-dimensional continuous attractor dynamics in the brain. We relate the empirical findings to dynamical models of grid cells, to generate constraints on the mechanisms that underlie grid cell response.

Results

We examine several datasets of grid cell recordings in their entirety. The results reported below include all simultaneously recorded cell pairs from these datasets, in which both cells of the pair share a common spatial period and meet a modified gridness score that includes cells with regular triangular grids, even if the triangles are not equilateral (see Online Methods).

Identical spatial responses up to 2-d translation

We examine spikes from neurons recorded simultaneously from the same or nearby tetrodes. The activity peaks of a sample pair (Fig. 1b) are arranged in the spatially periodic firing patterns characteristic of grid cells. Our definition of the spatial responses of grid cells, here and in the rest of this work, is the set of locations of the firing peaks. Six parameters are sufficient to characterize any periodic tiling in 2-d, regardless of the shape of the tiles³⁴. Thus, the spatial response of an individual cell in a particular environment is well-described by four parameters for the angles and lengths of two primary lattice vectors (Fig. 1c, inset), with two additional parameters that specify the 2-d spatial phase of the lattice, relative to some reference phase or location.

We find that cell pairs from the same or nearby tetrodes have extremely similar values for the first four parameters (Fig. 1c, N = 223 cell pairs: 24 from ref. 20; 97 from ref. 35; 12 from ref. 30; 90 from ref. 31). This is the case even though the cells have very different spatial phases (Fig. 1d), i.e., even when the cells are active in complementary parts of the environment. The relative phase between cell pairs, defined as the difference in their spatial phases, appears to be uniformly distributed (N = 223 cell pairs) over the unit cell of the lattice (Fig. 1d; consistent with similar result from ref. 20).

Cell-cell relationships more stable than single cells

We next examine the stability over time of each cell’s response and of cell-cell response relationships. Without any detailed analysis, the fact that a clear grid pattern is visible in the responses of individual neurons over a 20-minute recording session means that the individual spatial phases remain essentially constant over the session; if the phase shifted over time, the cell would fire at these different phases, and the grid response would be washed out. It follows directly that the relative phase between cells of the same spatial period and orientation will also be constant over that interval.

In this analysis, we probe the grid cell responses over longer time intervals: cells are recorded in an environment, then following an interval in which the animal is tested under varying conditions and environments, the cells are recorded again in the original environment (Fig. 1e). The elapsed time between recordings in the original environment is > 60 minutes. We find that cells that shared essentially identical values of the first four grid parameters in the first measurement (Fig. 1b,c) continue to share essentially identical parameter values in the subsequent measurement in the original environment (Fig. 1f, N = 84 cell pairs from refs. ^30,31).

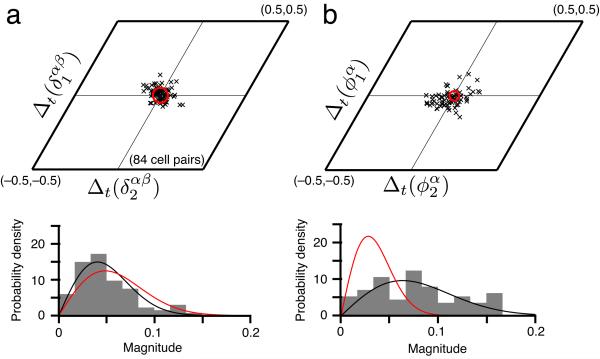
Moreover, the relative phases between cell pairs remain essentially constant over this interval (Fig. 2a, N = 84 cell pairs), consistent with continuous attractor dynamics that stabilizes cell-cell relationships. However, this stability of relative phase between cells may be attributable to the stability of the phases of individual cells across visits to the original environment. To differentiate between the two possibilities, we therefore compared the stability in the spatial phase of single cells with the stability of relative phase between cells. We find that, notably, the relative phase between cells is more tightly preserved than the phase of each cell (Fig. 2b), strongly suggesting a low-dimensional internal dynamics that yokes together the responses of different cells in the network, rather than spatially informative external cues.

Figure 2.

Across time in familiar environments, the relative phases between cells are more stable than the phases of single cells. (a) Top: The difference across time (trials separated by > 60 mins) in the relative phase between cell pairs is clustered near zero (black x’s, see Online Methods). Red circle: uncertainty in estimating relative phase differences (see Online Methods for error analysis). Bottom: Normalized histogram of the magnitudes of these relative phase differences (gray), with the null distribution (red), in which phase differences are not significantly different from zero and drawn independently from a Gaussian with standard deviation equal to the uncertainty in phase estimation. The null distribution of magnitudes is Rayleigh. Black: best-fit Rayleigh distribution to the data. (b) Difference across time (i.e., trials) of the phase of single cells (top), and the normalized histogram of magnitudes (bottom). Black, red defined similarly as in a. The data in a are not significantly different from the null hypothesis, while those in b are (a: P = 0.58 » 0.05, b: P « 10–4 under the F-test for whether the data and the null distribution come from a distribution of the same variance). Finally, P < 0.001 under the F-test for whether the data in a, b (bottom) come from a distribution of the same variance.

Cell-cell relationships stable despite grid distortions

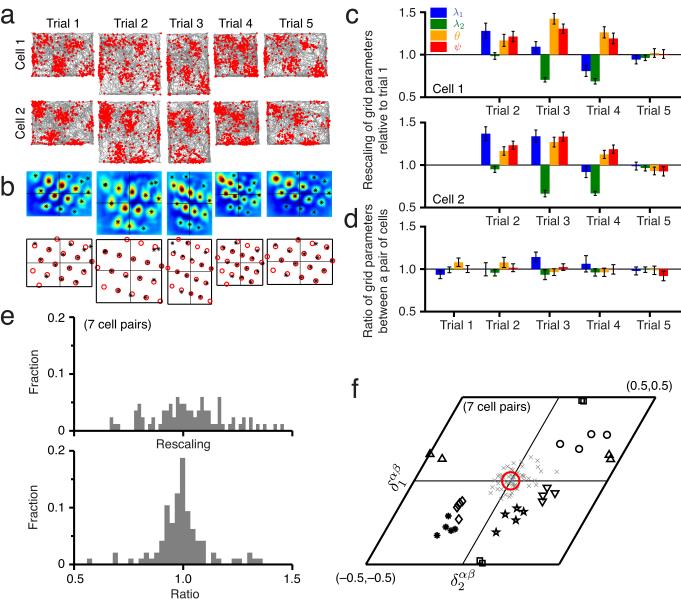
Next, we test pairwise relationships between grid cells that undergo a non-uniform rescaling of their individual grid responses when a familiar enclosure is suddenly resized³⁰ (Fig. 3a,b). This rescaling constitutes a major change in the responses and grid parameters of individual cells (Fig. 3c). But despite rescaling, the ratios of the first four grid parameters between cell pairs remain fixed very close to 1, indicating that these parameters change in tandem across the population (Fig. 3d). This result holds for all cell pairs (Fig. 3e, 7 cell pairs from ref. 30).

Figure 3.

Grid parameter ratios and relative phases are stable even when grid parameters are rescaled as the environment is resized. (a) Firing fields of two simultaneously recorded cells in a familiar environment (trials 1, 5) and resized versions of the familiar environments (trials 2, 3, and 4). (b) Spatial crosscorrelograms for the cell pair (top) and the best-fit template lattices (bottom). Asterisks denote local peaks in the crosscorrelogram. (c) Each grid parameter for cell 1 (top) or cell 2 (bottom) normalized by the value from trial 1. The parameters are substantially rescaled across trials 2–4.Error bars indicate ± 1 s.d. (Online Methods). (d) The ratio, between cells 1 and 2, of each grid parameter, for each trial. The ratios are statistically very close to one, despite the significant rescaling in each cell, seen in c. Error bars indicate 1 ± s.d. (Online Methods). (e) Top: Histogram of all grid parameters for the 11 cells in the resizing experiments from trials 2,3,4 normalized to the corresponding value from trial 1. Bottom: Histogram of the ratios of all grid parameter values between cells 1 and 2 for all 7 cell pairs from trials 1–4. This distribution is strongly peaked at 1 and different from the distribution at top. The Kolmogorov-Smirnov test for whether the two data samples come from the same distribution produces P < 0.001. The F-test for whether the two data samples come from a distribution of the same variance produces P < 0.001. (f) The relative phases for the 7 cell pairs span the unit cell (each black symbol represents a different cell pair; each marker for a given symbol represents a different trial). Gray x’s: relative phase differences, computed across all cell pairs and trials. Red circle: uncertainty in the relative phase difference magnitude (Online Methods). The relative phase differences are not significantly different from zero (P ≈ 0.6 » 0.05 for the same null hypothesis as in Fig. 2).

Crucially, the relative phases between cells remain nearly constant (Fig. 3f) despite the changes in grid cell responses, and the constancy of relative phases is independent of whether the cells have similar or very different phases relative to each other (Figs. 3f and 6). Thus we see that relative phase is strongly conserved even when the responses of single cells – influenced by changing external cues – have changed significantly, again strongly suggesting a 2-d state space and simultaneously suggesting that internal dynamics rather than external cues are responsible for the low-dimensional response.

Figure 6.

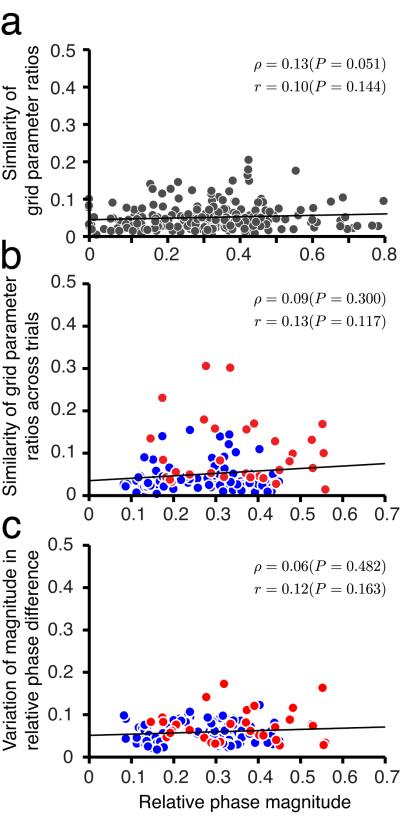
Stability of cell-cell relationships is independent of distance in spatial phase. (a) Parameters between cell pairs (223 cell pairs from Fig. 1c,d) in the same network are very similar (as reported in Fig. 1), and moreover, the degree of similarity does not vary with the difference in spatial phase (i.e. magnitude of relative phase) between cells (Parameter similarity is defined as the square-root of the squared deviation of parameter ratios from 1, averaged over all parameters per pair). Each dot represents one trial from one cell pair. Black: linear regression; p : Spearman’s rank correlation; r : Pearson’s product-moment correlation. (b) The stability of parameter ratios between cell pairs across rescaling trials (red dots, 7 pairs from Fig. 3f) and novel enclosure trials (blue dots, 24 pairs from Figs. 4 and 5) is independent of the pair’s relative phase. (c) The stability of relative phase (mean of magnitude of relative phase differences) across rescaling and novel enclosure trials is independent of relative phase between cells in a pair (same dataset and color-coding as in b).

Constancy of cell-cell relationships without place-cell stability

The preceding results are consistent with a population response that is confined to a 2-d manifold: Given the spatial response of one cell, the responses of the others are always predictable, differing from the single cell only by a fixed 2-d phase shift, which remains invariant across conditions. However, it remains possible that, rather than arising from attractor dynamics generated within the grid cell network, the low-dimensional response of grid cells is externally imposed: by sensory cues from the familiar room, that somehow are flexible enough to permit rescaling of individual responses yet rigidly force fixed relative phases; or more plausibly, by inputs from the hippocampus.

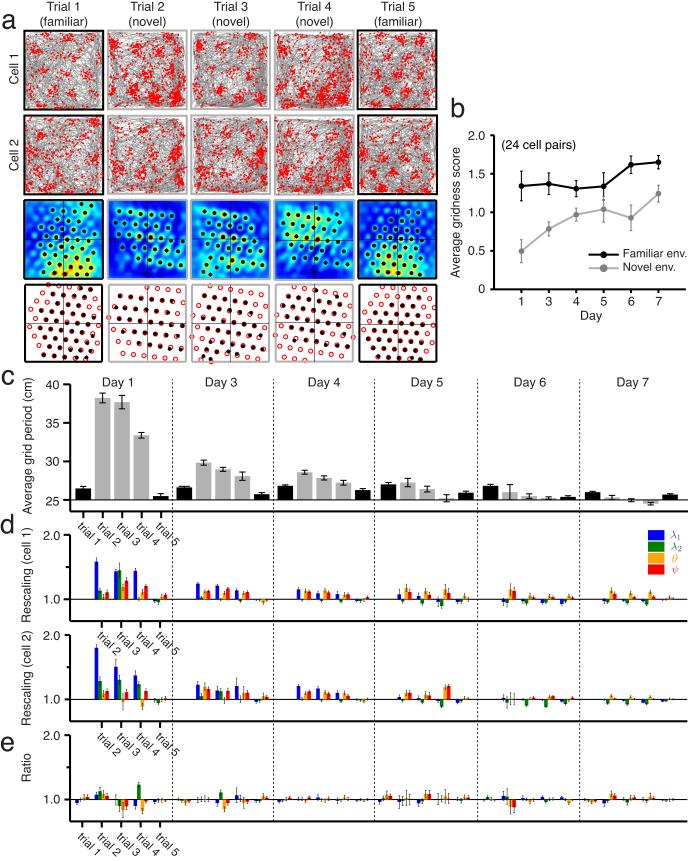
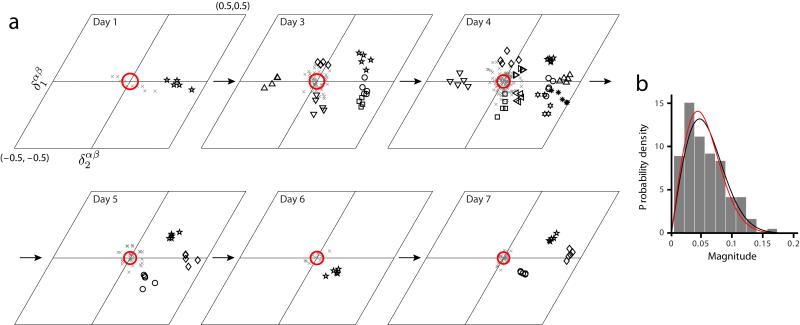
In an attempt to address these possibilities, we analyze grid cell responses from animals’ first exposures to novel environments. Grid cells are recorded first in a familiar environment, then in a novel environment, then again in several subsequent sessions in the novel environment as it becomes gradually more familiar³¹. In the first exposure to a novel environment, the spatial periods of grid cells expand suddenly, and the responses become less regular (Fig. 4a-c, 24 cell pairs from ref. 31). As the novel environment becomes more familiar, significant changes occur: the responses become more grid-like (Fig. 4b), and the grid periods contract steadily (Fig. 4c). Indeed, the four parameters of the grid response all change in the novel environment then relax back over days to values seen in familiar environments (Fig. 4d), while the environmental sensory input remains unchanged. This suggests that the response of grid cells and their relationships are not determined, and by extension, not stabilized, by the environmental sensory input during this contraction period. With this in mind, we next examine the relationships of grid parameters between cells. We find that the ratios of each grid parameter between cell pairs remain close to unity in the novel environment, as in familiar environments, starting with the very first exposure in the novel environment (Fig. 4e), and continuing throughout the period of contraction of the grid period. Again, crucially, we find that the relative phase between cells remains essentially unchanged between the familiar environment and the very first exposure to a novel environment (Fig. 5, 24 cell pairs from ref. 31), despite the large changes in the grid responses of neurons, and thus in their absolute phases. The relative phase between cells continues to remain fixed as the grid response shrinks over repeated exposures to the novel environment (Fig. 5).

Figure 4.

Grids become less stable and expand in novel enclosures, but grid parameter ratios remain stable. (a) Firing fields of pairs of simultaneously recorded cells in a familiar environment (black squares) and novel ones (gray squares) across five consecutive trials on one day, and the corresponding crosscorrelograms and best-fit template lattices. Note that on different days, the recordings involve different cells from the same tetrodes in the same area in the animal (Supplementary Fig. 5 for all cell pairs). (b) Development of average modified gridness in novel environments (gray) across seven days. The grid score gradually approaches that measured in familiar environments (black) (24 cell pairs, from ref. 31; means ± s.e.m.). (c) Change, across trials and days in the novel environment (gray), of the average grid period. Average grid period is the mean of the first two grid parameters across all cells in a trial (means ± s.e.m. 24 cell pairs total: 1, 6, 10, 3, 1, and 3 on days 1, 3, 4, 5, 6, and 7, respectively; no cells in day 2 passed the gridness criterion). The grid period significantly rescales in a novel environment, compared to when measured in the familiar environment (black), then gradually relaxes to its original value over seven days. (d) Grid parameters of one typical cell pair from each day (all cell pairs shown in Supplementary Fig. 5), normalized by the corresponding parameter values from the first trial (familiar environment) of the day. Clusters of four narrow bars represent the four parameters, in the same ordering and color scheme as in Figs. 1 and 3. Error bars indicate ± 1 s.d. (Online Methods). (e) Grid parameter ratios for the two cells, across trials and days. Almost all these ratios are statistically indistinguishable from 1 (for all cell pairs, see Supplementary Figs. 5 and 6). Error bars indicate ± 1 s.d. (Online Methods).

Figure 5.

Relative phase remains stable in novel enclosures. (a) The relative phases of the cell pairs (each distinct symbol represents a pair), across different trials and days (N = 24 cell pairs from ref. 31, across all 7 days). Gray x’s: the relative phase difference for every trial and all pairs. Red circle: uncertainty in the magnitude of relative phase differences (Online Methods). (b) The relative phase differences are not significantly different from zero for the same null hypothesis as in Fig. 2 (P = 0.38 » 0.05 under the F-test for whether the data and the null distribution come from a distribution of the same variance).

Because the animal in a novel space has not yet learned to associate external sensory cues with location^36,37, and because external cues remain fixed while the grid responses shrink over several days, it follows that the relationship between grid cells and the external world is less stable than is the relationship between grids cells. It is therefore unlikely that external sensory cues are stabilizing cell-cell relationships across novel and familiar environments.

In contrast to grid cell responses in the novel environment, simultaneously recorded place cells underwent complete remapping³¹ – defined as the loss of some of their firing fields and gain of others, with little preservation of spatial correlations between place cell firing fields. Like grid cells, place cell firing fields also expanded, then shrank, but to a much lesser extent than the grids, and for a shorter time. The remapped responses were not immediately stable, taking hours to stabilize³¹ (see also refs. ^25,38-40 for similar results on place cell remapping). Thus, hippocampal representations, and by extension, place cell-grid cell relationships, are in flux while cell-cell relationships between grid cells remain stable, suggesting that hippocampal input is not stabilizing relative phases between grid cells in the transition from familiar to novel environments, and within the novel environment. Taken together, these findings suggest that the hippocampus cannot be generating and feeding forward the 2-d stable responses observed in grid cells.

The above result is not inconsistent with the finding that hippocampal inputs seem required for grid cell activity⁴¹. A reduction of excitatory drive from the hippocampus and diminished activation of grid cells can, if the recurrent connections between grid cells are dominantly inhibitory^42,43, result in a failure of the recurrent connections to induce population patterning and low-dimensional dynamics, as in the models of refs. ^15,41. Hippocampal inputs might also correct path integration errors by selecting the appropriate population state for a given location from a set of stable population patterns^23,44,45, thus enabling accurately patterned spatial grid cell responses over a trajectory¹⁵. In either of these cases, the 2-dimensionality of the grid cell population response is intrinsic to the entorhinal cortex, but abolishing hippocampal drive may abolish spatial patterning.

We may conclude, first, that the grid cell population response is restricted to the same 2-d manifold at the first exposure to novel environments as in familiar environments, and second, that this restriction to the 2-d manifold cannot easily be ascribed to external sensory cues or hippocampal inputs, because relative phases and parameter ratios are stable even when these inputs are not.

Smoothness (continuity) of 2-d manifold

We next more closely examined the 2-d manifold of stable grid parameters and relative phases, to determine whether it exhibits a granular or “lumpy” structure, in which cell-cell stability is dependent on cell-cell similarity. A scenario in which cells with similar spatial phases conserved their relationships with each other more strongly, would be consistent with distinct subnetworks of cells with similar spatial response patterns stabilizing each other and not others with more dissimilar responses. Thus, we reexamined the results from familiar, rescaled, and novel environments, plotting parameter ratios as a function of relative phase between cell pairs. Parameter ratios were consistently close to one, independent of the distance in phase between cells (Fig. 6a). Importantly, the stability in cell-cell relationships across rescaled and novel enclosure trials, as measured by stability of parameter ratios (Fig. 6b) and stability of relative phases (Fig. 6c), did not vary with relative phase magnitude between cell pairs. Therefore, up to experimental resolution, the 2-d manifold of states is continuous.

Stability (attractiveness) of the 2-d manifold of states

We have established that the grid cell population response is localized to the neighborhood of a 2-d manifold, over extended periods of time and across varying external conditions that induce significant changes in the grid cell responses. Further, this localization is very likely due to internal recurrent dynamics, not a low-dimensional external input. What can we say about the dynamical stability of the 2-d manifold?

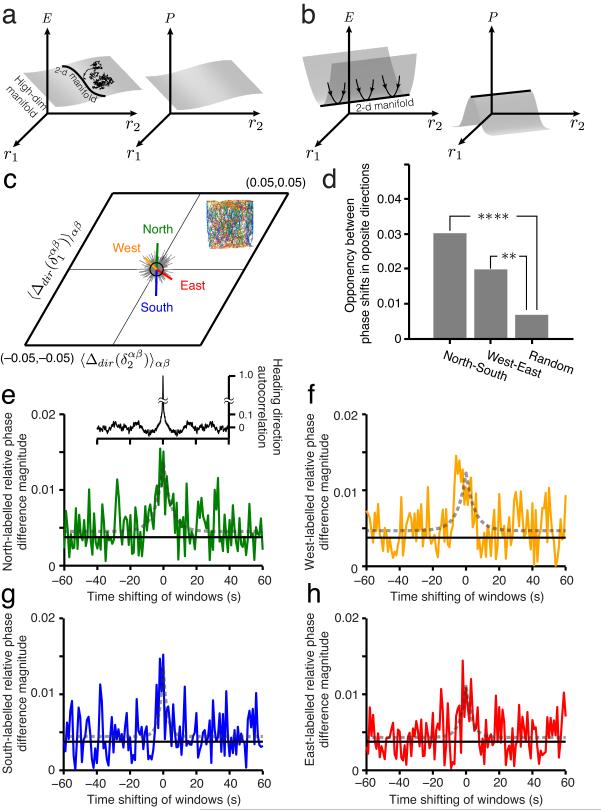
Real-world dynamical systems are localized to their stable or attractive states. They are seldom (with vanishing probability) found at or near unstable fixed points, precisely because such points are unstable and the smallest perturbation will drive the system away. Conversely, the dimensionality of state space occupied by the system is indicative of the dimensionality of the attractive states of the system. If a low-dimensional manifold is stable but is part of a higher-dimensional manifold of stable fixed points (Fig. 7a), then high-dimensional noise, however small, will cause the system to random-walk through the larger manifold⁴⁶. The system will consequently be found to inhabit any of the states across all dimensions of the stable higher-dimensional manifold. Grid cells are likely subject to high-dimensional internal noise: For example, stochastic vesicle release in synapses⁴⁷ causes independent perturbations in every postsynaptic neuron (noise dimension ~N, where N is the number of neurons). An analysis of spiking variability as a source of noise in grid cells is given in the SI (Supplementary Fig. 4). The fact that grid cells nevertheless primarily occupy the neighborhood of a 2-d manifold of states, in which cell-cell relationships are tightly conserved, suggests that the 2-d manifold is attractive (Fig. 7b) and that locally, the attractive manifold has a dimension neither greater than nor smaller than 2.

Figure 7.

Evidence of external perturbation and attractor dynamics in grid cell activity (a-b) Schematic energy landscape (left) and occupation probability (right) plots of a dynamical system. The independent variables on the plots depicting energy (left) and probability density (right) as heights are the firing rates of the neurons in the network. If the energy landscape has a flat plateau (a, left) of dimension D > 2, in which the 2-d manifold is embedded (depicted as a line), the system will likely be found off the 2-d manifold because there is no specific restoring drive back to it (a, right). When there is a 2-d valley in energy (b, left), the system state will be localized to the 2-d manifold (b, right) even in the presence of noise. (c) Inset: animal trajectory from one trial color-coded (green, blue, red, yellow) by the instantaneous movement direction (North, South, East, West quadrants, respectively). Main plot, green vector: the difference in relative phase between cell pairs, computed as the relative phase obtained from spikes obtained only during Northward trajectory fragments minus the relative phase obtained from all spikes in the trajectory, averaged across all cell pairs (223 pairs). Gray vectors: Samples from the null hypothesis of randomly segmenting the full trajectory into four sets of fragments of the same average lengths as the directional fragments, without directional specificity. Black circle: one standard deviation of the null hypothesis distribution (Online Methods). p -values for the directional shifts in relative phase under null hypothesis: North (P = 0.0004), West (P = 0.0444), South (P = 0.0003), East (P = 0.0201). (d) Opposing shifts in relative phase from opposing trajectory directions: North-South (****P < 10⁻⁴), West-East (**P < 0.0014 ) (Online Methods). (e-h) Green: Directional shifts induced in relative phase decay as the spike selection windows spanning Northward trajectory fragments are shifted in time, 1 second at a time, away from the centers of those directional segments, to include spikes emitted just before or after Northward movements. Black solid line: Radius of black circle from c. Gray dotted curve: Best-fit Laplace distribution with zero mean. Inset: Autocorrelation of movement direction in trajectories.

Besides the deduction, above, that the grid cell system is subject to perturbations off the attractor through internal stochastic dynamics, we find evidence that external perturbations, in the form of velocity inputs, drive the grid cell system away from the 2-d manifold. To see this, we select all the spikes emitted by a cell during parts of the trajectory when the animal is headed ‘northward’ (north ± 45deg), to form a North spatial activity map. We then compute the relative phase between a cell pair only for the North maps of each. The difference between this relative phase and the relative phase computed over the full trajectory is the perturbation off the attractor that northward motion induces in the state. All grid cells in our analysis have negligible directional tuning (Supplementary Fig. 2-2), thus changes in relative phase cannot be attributed to a direct velocity modulation. We do the same for the South, East, and West conditions. The resulting directional shifts in relative phase are statistically significant, compared to controls computed from similarly sized trajectory fragments unsorted by heading direction (Fig. 7c,d: data from the same cells in Fig. 1c,d). The shifts in relative phase between cells are consistent with the respective heading directions (Fig. 7c), suggesting that these shifts are indeed due to directional velocity input to the system. Thus, ongoing movements push the network away from the attractor by causing small deformations of the population pattern, in the form of a slight stretching of the population pattern along the direction of motion.

Finally, we examine the dynamics of perturbation by sliding the spike-selection windows in time relative to the centers of e.g. the Northward trajectory fragments (see Online Methods). We see that the shift in relative phase decays as the window is slid by a few seconds, and the decay time-constant is very similar to the autocorrelation time for directional motion in the animal trajectories. Thus, the off-manifold (perturbed) components of the network state relax back to the 2-d manifold on a time-scale similar to or faster than the few-second time-scale on which the perturbing input changes. The quick return of the system back to the 2-d manifold of states after perturbation from the external velocity input is direct evidence that the 2-d manifold is attractive.

Discussion

Summary

We have shown that, over short times and in familiar enclosures, the spatial responses of individual grid cells are well-characterized by a low-dimensional set of six parameters, with essentially the only difference between cells in the same network given by a 2-dimensional phase representing a rigid translation of the same basic response pattern. Over time and across environmental manipulations, the responses of individual grid cells change, and thus the parameters that describe their responses vary. Therefore, the responses of an individual grid cell are not described by a single set of six parameters.

Crucially, however, the dimensionality of the population response remains invariant. The responses of different grid cells are yoked tightly together: Over time or with experimental manipulation, when the spatial response patterns of the individual neurons change significantly – not only through rigid rotations but anisotropic and isotropic deformations of the grid pattern through stretching – the grid parameter ratios and relative phases between simultaneously recorded neurons in each network or module remain essentially constant (Cells with distinct grid periods – i.e., cells from different networks – could never share a stable spatial phase relationship even if all single-neuron grid parameters were perfectly stable, because the relative spatial phase between two perfectly periodic patterns of different frequency will necessarily precess relative to each other across cycles). In familiar enclosures, where stability may be attributed to external cues, we show that the cell-cell relationships are more stable than single-neuron responses, which argues against the external cue hypothesis. Cell-cell relationships persist with the same fidelity immediately upon entering novel environments, even though landmark cues suddenly change and remain unassociated with specific locations, while place cell responses continue to change, arguing strongly for stabilizing constraints within the grid cell system.

Thus, population activity is confined to the immediate vicinity of a 2-d manifold, across time and across conditions in different environments. Confinement of the system to a 2-d manifold despite stochastic internal dynamics and external velocity-driven perturbations off the manifold suggest that the 2-d manifold of states is an attractor.

Relationship to past work and implications for models

A glimpse that the responses of different grid cells are yoked together was afforded by the data of ref. 24 (not included in our present analysis): the spatial phases of ~ 5-9 simultaneously recorded grid cells shifted when the animal was moved from one environment to another, and the shifts appeared to be of a similar magnitude and direction across cells. However, both environments were familiar, so that hippocampal representations were stable (albeit different), and external cues could be used to provide locational information. Thus, without a comparative analysis of variability of phase within and between cells in a single environment, or an experiment involving destabilized hippocampal representations and external cues, the qualitatively different possibility of feedforward stabilization by hippocampal inputs or external cues could not have been ruled out.

Intracellular recordings in head-fixed animals navigating through virtual environments^48,49 show that grid cell membrane potentials exhibit a substantial DC depolarization at the firing field locations. This is consistent with excitatory (or disinhibitory) network drive that depolarizes neurons for the duration of a field. However, given that the intracellular recordings cannot distinguish between feedforward and feedback network inputs, and do not examine the structure and dimensionality of population activity, they do not provide specific evidence for continuous attractor models.

We have shown through population analysis that each grid cell network is localized to a 2-d manifold and that the manifold is attractive, which constitutes specific and direct evidence in support of continuous attractor network models of grid cell activity^12–15,22.

To be consistent with our findings, models of populations of grid cells need to include recurrent interactions that constrain the system to lie on a 2-d continuous attractor. The translation-invariant recurrent connectivity patterns of refs [2,4,12,14,15,22] are examples of such an interaction. Within the constraint of 2-d continuous attractor dynamics, however, models of grid cell networks may be quite different: Some consist of a single recurrent network with a 2-d attractor, in which the grid cells integrate velocity inputs^12,14,15. In others, the 2-d dynamics of grid cells arises from the feedforward summation of inputs, from two 1-d ring attractors, each of which integrates one component of animal velocity⁵⁰. In future work, it will be interesting to distinguish experimentally between such alternatives.

To conclude, our analysis contributes strong new evidence (see also refs. ^{10,11, 19}) supporting the idea that the brain uses low-dimensional continuous attractor dynamics in its integration and memory functions.

ONLINE METHODS

Binning and rate maps

Cell-sorted spikes of putative grid cells from foraging rats were assigned to (1cm × 1cm) spatial bins derived from position samples taken at 50 Hz. The number of spikes assigned to each bin was divided by the animal’s total dwell time in that bin, to remove the effects of inhomogeneous spatial exploration on estimating the probability of spiking at each location. This defines the rate map. Smoothed rate maps were generated by convolving the rate maps with a two-dimensional Gaussian kernel (σ = 4 bins).

Autocorrelations and crosscorrelations

To characterize the spatial response patterns of grid cells, we computed spatial autocorrelations from the smoothed rate maps of individual cells. To compare pairs of cells, we computed spatial crosscorrelations from the smoothed rate maps of simultaneously recorded cell pairs. If the smoothed rate maps are R₁ and R₂, both spatial correlations are generated as follows:

$$\gamma (u,v)=\frac{\sum _{x,y\in \Gamma }\left[R_1\right(x,y)-{\overline{R}}_{1,\Gamma }]\left[R_2\right(x-u,y-v)-{\overline{R}}_{2,\Gamma }]}{\sqrt{\sum _{x,y\in \Gamma }{\left[R_1\right(x,y)-{\overline{R}}_{1,\Gamma }]}^2\sum _{x,y\in \Gamma }{\left[R_2\right(x-u,y-v)-{\overline{R}}_{2,\Gamma }]}^2}}$$

where is y(u, v) the correlation coefficient at the bin (u, v), Γ is region of spatial overlap between R₁ and R₂, and ${\overline{R}}_{i,\Gamma }$ is the mean of R_i(x,y) within the region Γ. For autocorrelations, R₁ replaces R₂.

Modified gridness score

The standard gridness score^35,51 penalizes any regular grid pattern if it is not of an equilateral triangular pattern (Supplementary Fig. 1a,b). A novel scoring procedure was proposed⁵², with the aim of assigning high scores despite elliptical distortions in a hexagonal grid. However, it was limited by the fact that either the major or minor axis of the circumscribed ellipse was always assumed to pass through one of six nearest peaks. We used a modified gridness score that more generally allows both isotropic (equilateral triangle) and anisotropic (squeezed or stretched) grids to get a high score. For maximal sample size, and to test in principle the dimensionality of the grid cell response, it is important to include cells with anisotropic triangular grids: it is critical to determine whether deformed grid responses still lie on a low-dimensional manifold.

The modified gridness score is defined on the autocorrelogram of a cell. We first apply a transform on the correlogram that maps the central lattice cell (given by the six peaks nearest the center) into a regular hexagon (Supplementary Fig. 1c Left). This transform is determined by mapping the ellipse that circumscribes the central cell into a circle via a combined rotation, rescaling, and rotation transformation. If the number of nearest peaks (defined as the six or fewer peaks whose distance from the origin is less than 2 times the shortest distance from the origin to a neighboring peak) is less than or equal to four, the transformation is not applied.

Given the transformed autocorrelogram, we define an annular region with inner radius R_i and outer radius R_o. We rotate the autocorrelation map in steps of 6° and compute the Pearson correlation between the rotated map and the original map with each confined to the annular region. The gridness for a given annular region is defined by the minimum difference between crests and troughs in rotated correlations:

$$\text{Gridness}(R_i,R_o)=\underset{◻}{\min }\left\{{\rho }_{i,o}\right(60°),{\rho }_{i,o}(120°\left)\right\}-\underset{◻}{\max }\left\{{\rho }_{i,o}\right(30°),{\rho }_{i,o}(90°),{\rho }_{i,o}(150°\left)\right\}$$

where ρ_i,o(Φ) is the correlation value when one map is rotated by angle Φ relative to another over the annular region defined by R_i,R_o.

We do this for various values of R_i and R_o, letting R_i change from 0.5r to r and R_o change from R_i+1 cm to 1.5r (or to the maximum allowed value based on the autocorrelogram), each independently and in steps of 1cm. r is the mean distance to the nearest six peaks from the center in the transformed autocorrelogram. The modified gridness of the cell is then defined as the maximum gridness score over these various annular regions.

Our results are not qualitatively changed if we use the former gridness scoring technique⁵²; they also do not qualitatively change if we use our technique with a higher threshold (= 0.5).

Cell selection

In this paper, we analyzed data sets from four different sources^20,30,31,35 (data^20,35 available at http://www.ntnu.no/cbm/gridcell). A modified gridness score was computed for each grid cell, and cells with a gridness score less than zero were rejected (Supplementary Fig. 2-1). (When we restricted our cell sample based on the gridness score more commonly used in the past, the sample become smaller but the qualitative results remained unchanged. Indeed, because the error in grid parameter estimation drops for more clean grid responses, the cell-cell relationships and ratios become slightly tighter.)

For pairwise analyses, we used all possible cell pairs that were simultaneously recorded in the same individual animal and shared a common grid period whose maximum difference between cells was smaller than 30% in the familiar enclosure (provided both members were above threshold on the modified gridness score). Cells above threshold that had no simultaneously recorded cells to pair with that also met the threshold for cell-cell comparisons, were also rejected from further analysis. Data from 223 cell pairs are shown in Fig. 1c,d, from numerous experiments (24 from ref. 20; 97 from ref. 35; 12 from ref. 30; 90 from ref. 31). Data from 84 cell pairs (75 cells) are shown in Figs. 1f and 2a,b, from both resizing³⁰ and novel enclosure experiments³¹, recorded in both trials 1 and 5. Data from the same cells in Fig. 1c are shown in Fig. 7c-h. Note that all grid cells from all datasets that met our gridness criterion happened to have extremely weak directional sensitivity (Watson U2 score < 10, by the scoring method of refs. ^35,52; Supplementary Fig. 2-2). In Figs. 3–5, cell pairs that have lower gridness than the fixed threshold in both familiar enclosures or in more than two intermediate trials were discarded, which results in 7 cell pairs in Fig. 3 and 24 cell pairs in Figs. 4 and 5.

Template matching algorithm to estimate grid parameters

We identified local maxima in the autocorrelogram and noted the coordinates and heights of the peaks. The local maxima whose heights were lower than 1% of the height of the global maximum were not considered as “local peaks”. We then generated a 2-dimensional template lattice. Any 2-dimensional periodic lattice centered at the origin is fully specified by the magnitudes (λ₁,λ₂) and orientations (ψ₁,ψ₂)=(ψ,θ–ψ) of two basis vectors (Fig. 1c). The angles are measured from the x axis. The template lattice is generated by populating the explored spatial environment by vertices whose locations are determined by the basis vectors and their translations. The lattice parameters are determined by finding values that minimize a cost function that quantifies the fit between the template and the data. The cost function is given by the sum of the squared distances from every data peak to the nearest vertex in the template lattice, weighted by the autocorrelation amplitude at that data peak:

$$C=\sum _{i=1}^n{w}_i{\Vert p_i-v_i\Vert }_2$$

where p_i is the (x,y) location of the data peak, v_i is the vector for the point in the lattice nearest to the i th data peak, w_i is the correlation coefficient at p_i, and n is the total number of peaks in the autocorrelogram.

The central peak of a crosscorrelogram is typically not at the origin, but shifted by some displacement vector $\overrightarrow{d}$ from the origin. Thus, 2 additional parameters $\overrightarrow{d}=(d_x,d_y)$ were estimated simultaneously with (λ₁,λ₂) and (ψ₁,ψ₂) by minimizing the same cost function in order to find the best-fit template lattice of the crosscorrelogram.

Relative phase, relative phase difference, and phase magnitude

Let ${\overrightarrow{\varphi }}^{\alpha }$ represent the phase of cell α, where the component ${\varphi }_i^{\alpha }$ is the phase along the i th lattice basis vector. The relative phase between cells α and β is then

$${\overrightarrow{\delta }}^{\alpha \beta }\equiv \left({\overrightarrow{\varphi }}^{\alpha }-{\overrightarrow{\varphi }}^{\beta }\right)\mathrm{mod}1$$

where “\”mod 1\” is understood to apply to each component. The relative phase between a pair of cells is closely related to the shift $\overrightarrow{d}$ in the peak of their spatial crosscorrelogram. If the two cells have precisely the same lattice parameters, then $\overrightarrow{d}$ will equal the relative shift of the two cells’ grid patterns. The oblique projection of $\overrightarrow{d}$ onto the two primary lattice vectors ${\overrightarrow{e}}_1$ and ${\overrightarrow{e}}_2$ produces the components $\left(d_1^{\mathit{proj}},d_2^{\mathit{proj}}\right)$. When the components are normalized by λ₁ and λ₂, respectively, and considered modulo 1, we get the relative phase:

$$\begin{array}{cc}\hfill & \left({\delta }_1^{\alpha \beta },{\delta }_2^{\alpha \beta }\right)=\left({\varphi }_1^{\alpha }-{\varphi }_1^{\beta },{\varphi }_2^{\alpha }-{\varphi }_2^{\beta }\right)\mathrm{mod}1\hfill \\ \hfill & =\left(\frac{d_1^{\mathit{proj}}}{{\lambda }_1},\frac{d_2^{\mathit{proj}}}{{\lambda }_2}\right)\mathrm{mod}1\hfill \end{array}$$

If the relative phase between the same two cells is measured in two different conditions (such as in distinct trials), we can define the relative phase difference as the difference in ${\overrightarrow{\delta }}^{\alpha \beta }$ between the two conditions. We will denote this as ${\Delta }_c\left({\overrightarrow{\delta }}^{\alpha \beta }\right)$, where C labels the condition. Relative phase differences are equivalent modulo 1 and representing them on the unit lattice cell with components in the interval [0,1) has the consequence that values close to zero will appear in the four corners of the unit cell (Supplementary Fig. 3a-b). To avoid this and map values close to zero together, we remap the unit lattice cell to the equivalent unit cell with components in the interval [−0.5,0.5). Thus, the relative phase difference at distinct times t₁,t₂ is given by:

$$\begin{array}{cc}\hfill & {\Delta }_t\left({\overrightarrow{\delta }}^{\alpha \beta }\right)=f\left[\left({\overrightarrow{\delta }}_{t_1}^{\alpha \beta }-{\overrightarrow{\delta }}_{t_2}^{\alpha \beta }\right)\mathrm{mod}1\right]\hfill \\ \hfill & f\left(\overrightarrow{x}\right)=\left\{\right(\left(\right(x_{\downarrow }1-1,x_{\downarrow }2-1)‘‘\text{if}"x_{\downarrow }1\ge 0.5‘‘\text{and}"x_{\downarrow }2\ge 0.5@(x_{\downarrow }1-1,x_{\downarrow }2)‘‘\text{if}"x_{\downarrow }1\ge 0.5‘‘\text{and}\hfill \end{array}$$

where ${\overrightarrow{\delta }}_{t_1}^{\alpha \beta }={\left({\delta }_1^{\alpha \beta },{\delta }_2^{\alpha \beta }\right)}_{t_1}$ and ${\overrightarrow{\delta }}_{t_2}^{\alpha \beta }={\left({\delta }_1^{\alpha \beta },{\delta }_2^{\alpha \beta }\right)}_{t_2}$ are relative phases between cells α,β at time t₁ and t₂. The function $f\left(\overrightarrow{x}\right)$ maps (x₁,x₂) within the interval [0,1) into [−0.5,0.5) by subtracting 0.5 from each component, if that component is greater than or equal to 0.5 (Supplementary Fig. 3c).

For relative phase, we take the relative phase magnitude to be of the form $\Vert {\overrightarrow{\delta }}^{\alpha \beta }\Vert ={\left({\delta }_1^{\alpha \beta }\right)}^2+{\left({\delta }_2^{\alpha \beta }\right)}^2+{\delta }_1^{\alpha \beta }{\delta }_2^{\alpha \beta }$ and similarly for relative phase difference magnitudes.

Error analysis

The error bar (∊) in Figs. 3c,d and 4d,e for the ratio of two uncertain quantities $\frac{{\lambda }_1}{{\lambda }_2}$ is given by the standard method of error propagation given a covariance matrix Σ for the uncertainties in λ₁ and λ₂. Σ is estimated via bootstrap resampling: given an original spike (discharge) map of M total spike locations, we create 100 new spike maps of M total spikes each, by picking spike locations from the original map one at a time, at random, and with replacement, from the original map. Next, we use these spike maps to generate rate maps using the same procedure as for the original, with the original trajectory data (i.e. with a normalization given by the same visitation frequency as the original spike map) and estimate grid parameters from the spatial autocorrelogram with the template matching algorithm. This procedure generates 100 samples of the grid parameters, from which we compute the covariance matrix as an estimate for Σ. The error for the ratio $\frac{{\lambda }_1}{{\lambda }_2}$ is given by:

$$\frac{{\lambda }_1}{{\lambda }_2}\pm ∊=\frac{{\lambda }_1}{{\lambda }_2}\pm \frac{{\lambda }_1}{{\lambda }_2}\sqrt{\frac{{\sum }_{11}}{{\lambda }_1^2}+\frac{{\sum }_{22}}{{\lambda }_2^2}-2\frac{{\sum }_{12}}{{\lambda }_1{\lambda }_2}}$$

The radius (r) of the red circles in Figs. 2a,b, 3f, and 5, signifies the measurement error of the differences across trials, in phase per cell (Fig. 2b) or in relative phase per cell pair (Figs. 2a, 3f, and 5). This measurement error is estimated by applying the same bootstrapping technique to every cell (pair), computing now the (relative) phase difference as defined above for each bootstrap sample, and then subtracting the mean of sampled (relative) phase differences for each cell (pair). The error in (relative) phase difference across (pairs of) cells is given by collapsing all the bootstrap samples of zero-mean (relative) phase differences and fitting a 2d Gaussian with a multiple of the identity matrix as a covariance to those samples (by expectation-maximization algorithm). The radius in the Figures is the square root of the estimated covariance.

Analysis of velocity-driven perturbation

Define cardinal direction labels as North (45° – 135°), West (135° – 225°), South (225° – 315°), or East (315° – 45°). Each time point t in the animal’s trajectory is labeled by the animal’s velocity at that time (given by the vector difference quotient between the position at t+Δt and t). Spikes that occur at time t are labeled by the trajectory direction label at that time. This produces four sets of trajectories and for each cell, four corresponding sets of spike maps, labeled by North, South, East, and West. For each direction, we generate rate maps and relative phases (as we did earlier for the full trajectory and full spike maps). For each cell pair, we thus obtain four “direction-labeled relative phases”, given by ${\overrightarrow{\delta }}_{\mathit{dir}}^{\alpha \beta }=\left({\overrightarrow{\varphi }}_{\mathit{dir}}^{\alpha }-{\overrightarrow{\varphi }}_{\mathit{dir}}^{\beta }\right)$ where dir ∈ {North, South, East, West} and α,β refer to the cells. We denote the relative phase for the full spike maps, obtained earlier, as $\left({\overrightarrow{\delta }}_{\mathit{full}}^{\alpha \beta }\right)$. The “direction-labeled relative phase differences” for each cell pair are defined as the differences between the direction-labeled relative phase and the full relative phase $\left(\mathrm{i}.\mathrm{e}.{\Delta }_{\mathit{dir}}\left({\overrightarrow{\delta }}^{\alpha \beta }\right)={\overrightarrow{\delta }}_{\mathit{dir}}^{\alpha \beta }-{\overrightarrow{\delta }}_{\mathit{full}}^{\alpha \beta }\right)$. The mean value of the direction-labeled relative phase difference, with the average taken over all simultaneously recorded cell pairs, is shown in Fig. 7c. It is written as ${\langle {\Delta }_{\mathit{dir}}\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }$.

To assess whether the shifts in relative phase as a function of motion direction are meaningful, we create a null hypothesis distribution by segmenting the full trajectory into continuous pieces of a length consistent with the lengths of the continuous pieces generated in the direction-labeled trajectory segmentation described above (the fragment length was set equal to the correlation time of the animal’s heading direction; a representative value of the heading direction correlation time across experiments is approximately 0.65 sec, and we chose 1.6 seconds to provide a window of at least two time constants). However, the segmentation did not correlate with movement along a specific direction. The segments resulting from this process were divided, randomly, into 4 sets of equal size. Consider one such set of directionally mixed or random segments, and label it “R”, in contrast to the (North, South, East, West) labels of the directional trajectory segments. The relative phase difference for this one set of directionally mixed trajectory segments is denoted ${\Delta }_R\left({\overrightarrow{\delta }}_R^{\alpha \beta }\right)={\overrightarrow{\delta }}_R^{\alpha \beta }-{\overrightarrow{\delta }}_{\mathit{full}}^{\alpha \beta }$. Averaging this relative phase difference for one set of trajectory segments, across all simultaneously recorded cell pairs, gives one sample of ${\langle {\Delta }_R\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }$, which can be seen as one gray vector in Fig. 7c. Repeating this procedure 400 times produces the 400 different gray vectors in Fig. 7c. The lengths of these vectors represent the expected magnitude of deviation from the full phase simply due to subsampling errors from subdividing the full trajectory into 4 sets, independent of directional effects. Thus, these vectors provide the null hypothesis for no directional motion effects on relative phase. We approximate the sampled distribution of vectors ${\langle {\Delta }_R\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }$ by a symmetric 2-d Gaussian with standard deviation σ². Using this distribution, the p-value of the mean direction-labeled relative phase differences, $l={\langle {\Delta }_{\mathit{dir}}\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }$, is given by:

$$p={\int }_{l^2}^{\infty }\exp \left(-\frac{r^2}{2{\sigma }^2}\right)\mathit{dr}$$

In Fig. 7d, we test the opponency of shifts in relative phase, for opposite movement directions, by computing the magnitude of the difference between opposing mean labeled relative phase differences, $\Vert {\langle {\Delta }_{\mathit{North}}\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }-{\langle {\Delta }_{\mathit{South}}\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }\Vert$ and $\Vert {\langle {\Delta }_{\mathit{West}}\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }-{\langle {\Delta }_{\mathit{East}}\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }\Vert$. The magnitude of opponency expected under the null hypothesis is given by the expected magnitude of the differences between the gray bars of Fig. 7c, i.e., by averaging $\Vert {\langle {\Delta }_R\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }^i-{\langle {\Delta }_R\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }^j\Vert$, where i and j index values of ${\langle {\Delta }_R\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }$ from the 400 samples shown in Figure 7c. This gives the height of the “random” bar in Fig. 7d. The fraction of samples with $\Vert {\langle {\Delta }_R\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }^i-{\langle {\Delta }_R\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }^j\Vert$ that is larger in size than $\Vert {\langle {\Delta }_{\mathit{North}}\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }-{\langle {\Delta }_{\mathit{South}}\left({\overrightarrow{\delta }}^{\alpha \beta }\right)\rangle }_{\alpha \beta }\Vert$, gives the p-value that the direction-labeled relative phase differences can be accounted for by the null hypothesis.

Analysis of relaxation from the perturbation

We tracked the mean shifts in relative phase for each cardinal direction as a function of time to examine the dynamics of perturbation off the attractor. First, we used the Northward direction-labeled trajectory fragments to define a corresponding set of time-windows to select spikes for analyzing relative phase along that movement direction. Next, we slid the same set of time windows forward, so that instead of being centered in time at the Northward fragments, they were centered 1 second after the center (in time) of each Northward fragment, and so on, in steps of 1 second. We did the same in the opposite direction, sliding the windows back. For each position of the windows, we computed the relative phase for spikes obtained from those windows, and subtracted from it relative phase obtained from the full trajectory. For each time-shift, we averaged the result across all 223 cell pairs in our dataset.

Analysis of stochastic dynamics

To investigate the variance of spiking in grid cells, we compute the interspike interval (ISI) distribution using firing times {τ_i} that are rescaled from the original firing times {t_i} via ${\tau }_i={\int }_0^{t_i}\lambda \left(t\right)\mathit{dt}$, where λ(t) is the time varying firing rate of the cell. λ(t) was approximated by sliding a rectangular window function along the spike train. The coefficient of variation (CV) in Supplementary Fig. 4, Left was derived from the rescaled ISI with Δt=0.5 seconds. The CV as a function of window size for 4 representative cells is shown in Supplementary Fig. 4, Right.