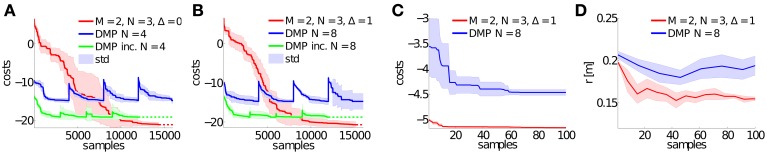
Figure 7.

Learning curves for the biped walker task. This figure illustrates the learning performance over 10 runs of the proposed approach using M = 2 synergies with N = 3 Gaussian basis functions. In (A) the time-shift variables Δs are not learned and set to zero. Whereas, in (B) also these Δs variables are adapted during learning. We compare to the dynamic movement primitives (DMP) with N = 4 Gaussians in (A) and to DMPs with N = 8 Gaussians in (B). DMP inc. denotes an incremental learning setup, where DMPs were initialized with the best result from the previous task. Generalizing to a new step height (r^* = 0.1 m) is shown in (C), where we applied the best learned policy for DMPSynergies from (B) and only optimized the weights β_1:2 for the two (fixed) synergies. The corresponding average step height over all steps is shown in (D). We compare to DMPs with N = 8 Gaussians.