Abstract
Normal-hearing listeners take advantage of differences in fundamental frequency (F0) to segregate competing talkers. Computational modeling using an F0-based segregation algorithm and auditory-nerve temporal responses captures the gradual improvement in concurrent-vowel identification with increasing F0 difference. This result has been taken to suggest that F0-based segregation is the basis for this improvement; however, evidence suggests that other factors may also contribute. The present study further tested models of concurrent-vowel identification by evaluating their ability to predict the specific confusions made by listeners. Measured human confusions consisted of at most one to three confusions per vowel pair, typically from an error in only one of the two vowels. An improvement due to F0 difference was correlated with spectral differences between vowels; however, simple models based on acoustic and cochlear spectral patterns predicted some confusions not made by human listeners. In contrast, a neural temporal model was better at predicting listener confusion patterns. However, the full F0-based segregation algorithm using these neural temporal analyses was inconsistent across F0 difference in capturing listener confusions, being worse for smaller differences. The inability of this commonly accepted model to fully account for listener confusions suggests that other factors besides F0 segregation are likely to contribute.
INTRODUCTION
Listeners with normal hearing have the ability to understand one talker in the presence of many other talkers. Pitch differences [e.g., due to fundamental-frequency (F0) differences] are one of the cues used by listeners to perceptually segregate concurrent harmonic sounds (e.g., vowels) and thus facilitate their ability to track one talker in the presence of others (e.g., Cherry, 1953; Brokx and Nooteboom, 1982; Scheffers, 1983a; Assmann and Summerfield, 1990; Bregman, 1990). When two equal amplitude synthetic vowels with the identical F0 are presented simultaneously, both vowels can be identified correctly with scores averaging between 40% and 70%. This result suggests that listeners are using cues other than F0 difference (such as spectral differences associated with the formants of the two vowels) for their identification. Identification of both vowels increases with increasing F0 difference, with only small additional improvement when F0 difference is larger than one to two semitones (e.g., Scheffers, 1983a; Zwicker, 1984; Summerfield and Assmann, 1991; Culling and Darwin, 1993, 1994; Assmann and Summerfield, 1994; Arehart et al., 1997; Summers and Leek, 1998; Arehart et al., 2005; Vongpaisal and Pichora-Fuller, 2007, see review by Micheyl and Oxenham, 2010).
Models of concurrent vowels are based on the assumption that one or both F0s needs to be identified for segregating the vowels prior to their identification (Scheffers, 1983b; Zwicker, 1984; Assmann and Summerfield, 1990; Meddis and Hewitt, 1992). Among all the existing models, the F0-based segregation model of Meddis and Hewitt (1992) was the only one that was successful in predicting the gradual increase in identification of both vowels with increasing F0 difference. Furthermore, Palmer (1992) successfully tested this segregation model by identifying both vowels using recorded responses from auditory-nerve (AN) fibers.
The improvement in identification of both vowels is thought to be largely due to the enhancement in F0 segregation (i.e., segregating two simultaneous vowels using F0 difference). Listeners can successfully adjust F0 of a harmonic tone complex to match the individual pitches of a concurrent vowel, but only when the F0 difference is four semitones or higher (Assmann and Paschall, 1998). However, most of the improvement in vowel identification usually occurs below one or two semitones, where listeners perceive a single pitch. This suggests that the improvement at smaller F0 differences might not be entirely due to F0 segregation. At non-zero smaller F0 differences, listeners may utilize temporal envelope cues (resulting from harmonic interactions between vowels) for their identification (Culling and Darwin, 1994). However, de Cheveigné (1999) varied the temporal envelope of each vowel by altering the starting phase of the harmonics and found no change in vowel identification. Larsen et al. (2008) found that the temporal representations of AN fibers can correctly estimate both F0s of concurrent harmonic tone complexes, which are separated by one or four semitones. Nevertheless, their study did not explore F0 segregation explicitly. The above-mentioned studies suggest that F0 segregation might be only one of the factors for the improvement in identification of both vowels.
One limitation of previous modeling efforts for concurrent vowel identification is that the models have been largely evaluated only based on overall percent correct. Thus, these large-parameter-space models are likely to be under-constrained, which limits their ability to identify the key factors involved in these effects. The present study was motivated by the idea that additional constraints could be applied to the models by testing their ability to account for the specific confusions made by human listeners, in addition to the overall pattern of improvement in performance as the F0 difference increases. Specifically, if the commonly accepted Meddis and Hewitt (1992) model fully represents the segregation and identification factors that contribute to concurrent vowel identification, then the ability of this model to account for listener confusions should be invariant with F0 difference.
Thus, in the present study concurrent-vowel confusion patterns made by human listeners were measured and characterized in detail. These data were used to quantitatively evaluate the ability of spectral patterns to account for listener confusions when no F0 difference was present. The potential contribution of cochlear signal processing was evaluated by comparing simple identification models based on acoustic and cochlear spectral patterns. To evaluate the potential contribution of temporal processing of AN-fiber responses, the spectral models were compared with a simple model based on neural temporal patterns. Finally, the ability of the Meddis and Hewitt (1992) F0-based segregation model to account for listener confusions was quantified as a function of F0 difference to evaluate whether other factors are needed to fully account for the improvement in concurrent vowel identification with increasing F0 difference.
CONCURRENT VOWEL IDENTIFICATION
Subjects
Five native speakers (ages = 20–28 yr and mean = 24 yr) of American English participated in this experiment. The subjects were screened using air conduction audiometry and tympanometry tests. All subjects had thresholds ≤15 dB HL between 250 and 8000 Hz, and also had normal tympanograms in each of their ears. All subjects signed an informed consent document prior to participation, which was approved by the Institutional Review Board of Purdue University.
Stimuli
A set of five vowels /i/, /ɑ/, /u/, /æ/, and /ɝ/ was used and identified on a computer screen by the words: “heed,” “hod,” “whod,” “had,” and “heard,” respectively. The vowels were generated using a cascade formant synthesizer (Klatt, 1980) written in matlab (The Math Works, Natick, MA, USA) with the same five formants and bandwidths (Table TABLE I.) that were used in numerous studies of vowel identification (e.g., Assmann and Summerfield, 1994; Assmann and Paschall, 1998; Summers and Leek, 1998).
TABLE I.
Formants (in Hz) for five different vowels. Values in parentheses correspond to bandwidth around each formant (in Hz, first column).
| Vowel | /i/ “heed” | /ɑ/ “hod” | /u/ “whod” | /æ/ “had” | /ɝ/ “heard” |
|---|---|---|---|---|---|
| F1 (90) | 250 | 750 | 250 | 750 | 450 |
| F2 (110) | 2250 | 1050 | 850 | 1450 | 1150 |
| F3 (170) | 3050 | 2950 | 2250 | 2450 | 1250 |
| F4 (250) | 3350 | 3350 | 3350 | 3350 | 3350 |
| F5 (300) | 3850 | 3850 | 3850 | 3850 | 3850 |
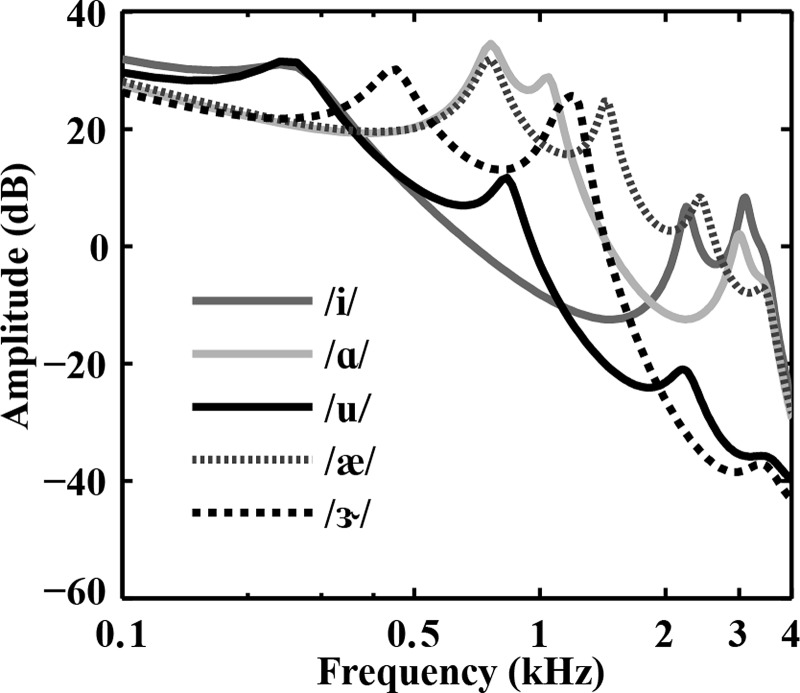
Each vowel had a static F0 and was 400 ms in duration (including 10 ms onset and offset raised-cosine ramps). Figure 1 shows the spectral envelopes for the five vowels that were computed using linear predictive coding. The locations and relative levels of formants differed for each vowel (Fig. 1). Concurrent vowels were created by adding two individual vowels through a signal mixer (see Sec. 2C). In each vowel pair (e.g., /i, u/), the F0 of one vowel (e.g., /i/) was always equal to 100 Hz while the F0 of the other vowel (e.g., /u/) was equal to 100, 101.5, 103, 106, 112, or 126 Hz (F0 differences of 0, 0.25, 0.5, 1, 2, and 4 semitones, respectively). Each F0 difference condition had 25 (5 × 5) vowel pairs. These pairs were further divided into three categories: identical vowel pairs (e.g., /i, i/), mixed vowel pairs (e.g., /i, u/), and reverse-mixed vowel pairs (e.g., /u, i/). The reverse-mixed vowel pair was similar to the mixed vowel pair except that the F0s between the two vowels were reversed. Overall, there were 150 vowel pairs (25 pairs × 6 F0 differences) for this experiment.
Figure 1.
Spectral envelopes for the five vowels computed using linear predictive coding. Legend indicates different vowels. The local maxima correspond to each formant. The level of first formant is greatest compared to the levels at the second and third formants for all vowels.
Instrumentation
The 30 individual vowels (5 vowels × 6 F0s) were created in matlab and saved in WAV file format (sampling rate = 24 414.06 Hz). The sykofizx program (Tucker-Davis Technologies, Alachua, FL, USA) was used for experimental design, stimulus presentation and data collection. Each vowel was output from a D/A converter (TDT RP2.1) and passed to a programmable attenuator (TDT PA5). For example, to generate the vowel pair for the 4-semitone condition, one vowel (F0 = 100 Hz) and the other vowel (F0 = 126 Hz) were then added by a signal mixer (TDT SM5). Finally, the pair was passed through a headphone buffer (TDT HB7) and delivered to the listener's right ear through Sennheiser HD 580 headphones. The individual vowels were presented at 65 dB SPL, so that the overall level of the vowel pair was ∼68 dB SPL. Listener's responses were recorded in the sykofizx program and data analyses were performed in matlab.
Procedures
For familiarization with vowel stimuli and the listening task, two stages of training were completed prior to collection of concurrent vowel data. In the first stage, participants heard 150 single vowels (5 vowels × 6 F0s × 5 repetitions) and were required to achieve ≥90% correct identification to proceed to the next stage. Participants responded using the mouse by clicking one of 5 buttons representing each vowel and feedback was provided. All participants met this criterion in the first set of 150 vowels except one who needed a second set. In the second stage, listeners heard the vowel pairs at three F0 differences (4, 1, and 0 semitone differences, in this order). For each F0 difference, there were 100 vowel pairs (25 pairs × 4 repetitions). Listeners responded using the mouse by clicking on one of 25 buttons in a 5 × 5 matrix representing each vowel-pair combination. Feedback indicated a correct response only when both vowels were identified correctly, in either order. For an incorrect response, the correct answer was displayed in the matrix. The 300 vowel pairs (100 pairs × 3 F0 differences) were repeated to each listener until they showed a gradual increase in identification of both vowels with increasing F0 difference. This criterion was achieved in two sets of 300 vowel pairs by three listeners and the other two listeners needed a third set. Thus, listeners had approximately 2–4 h of concurrent-vowel training before proceeding to final data collection. This testing stage had three listening sessions. In each session, listeners heard 100 vowel pairs (25 pairs × 4 repetitions) at each of the six F0 differences but the order of F0 difference was randomized. Listeners took approximately 1–1.5 h to complete each session. Feedback was provided as described earlier. The responses made by each listener were recorded to allow a more detailed analysis of percent correct identification and confusion patterns.
Results and discussion
Vowel identification
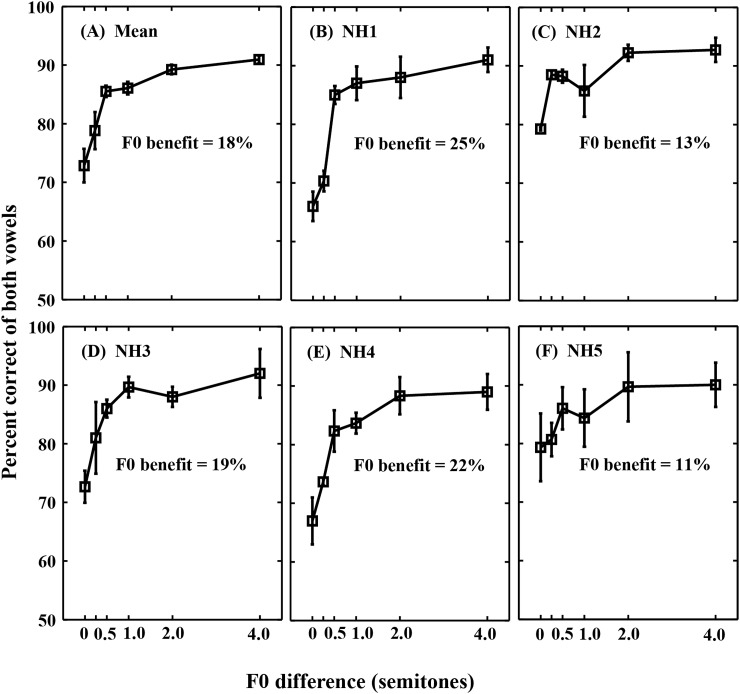
Figure 2A shows mean correct identification of both vowels as a function of F0 difference for five normal-hearing listeners. Consistent with previous results (e.g., Assmann and Summerfield, 1990, 1994; Summerfield and Assmann, 1991; Arehart et al., 1997; Summers and Leek, 1998), the identification of both vowels increased with increasing F0 difference; with very little improvement for F0 difference ≥ 2 semitones. The “F0 benefit” was quantified as the difference between the identification scores for F0 differences of 4 and 0 semitones; mean F0 benefit was 18%, also consistent with previous results. Although some individual differences were apparent [Figs. 2B, 2C, 2D, 2E, 2F], the scores for all listeners improved with increasing F0 difference (F0 benefit ranges from 11%–25%). These patterns of identification were qualitatively similar to those seen in previous studies.
Figure 2.
Mean correct identification of both vowels in the vowel pairs as a function of F0 difference for normal-hearing listeners. (A) Mean scores for five listeners. (B)–(F) Mean scores for individual listeners (NH1–NH5). Error bars denote ±1 SEM. F0 benefit (shown in each panel) is defined as the difference in identification scores between the 4- and 0-semitone F0 difference conditions.
A two-way repeated measures analysis of variance (ANOVA) between F0 difference and session was performed on the rationalized arcsine-transformed identification scores of both vowels (Studebaker, 1985). The main effects of F0 difference [F (5, 20) = 33.07, p < 0.001] and session [F (2, 8) = 7.08, p = 0.017] were significant. Only the first session was significantly different from the second session [F (1, 4) = 9.06, p = 0.039]. The interaction between F0 difference and session was not significant [F (10, 40) = 0.40, p = 0.937]. Since there was no significant interaction, the identification scores of both vowels were averaged across sessions for each listener and used in further analyses. The identification scores [Fig. 2A] significantly increased from 0 to 0.5 semitone F0 difference conditions [F (1, 4) = 47.19, p = 0.002]. A significant increase in identification scores was also observed between the 0.5- and 2-semitone conditions [F (1, 4) = 28.40, p = 0.006], between the 0.5- and 4-semitone conditions [F (1, 4) = 171.87, p < 0.001] and between the 1- and 4-semitone conditions [F (1, 4) = 122.54, p < 0.001].
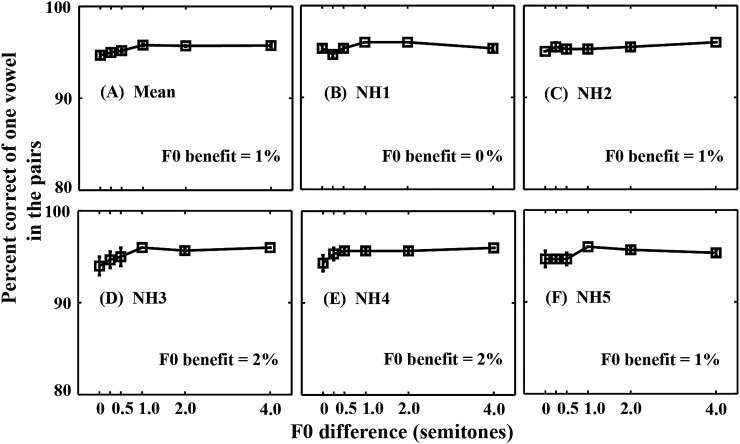
Figure 3A shows mean identification of one vowel in each of the pairs as a function of F0 difference. Across all F0 difference conditions, the mean identification scores for one vowel correct were quite similar (∼93%). The individual listeners also showed similar patterns of identification [Figs. 3B, 3C, 3D, 3E, 3F].
Figure 3.
Mean correct identification of one vowel in each of the vowel pairs as a function of F0 difference for normal-hearing listeners. (A) Mean scores for five listeners. (B)–(F) Mean scores for individual listeners (NH1–NH5). Error bars denote ±1 SEM. F0 benefit is shown in each panel. Note that the scale of the ordinate is different from Fig. 2.
A two-way repeated measures ANOVA between F0 difference and session was performed on the rationalized arcsine-transformed identification scores of one vowel correct (Studebaker, 1985). The main effect of F0 difference was significant [F (5, 20) = 9.95, p < 0.001], but there was no significant effect of session [F (2, 8) = 1.34, p = 0.314]. The interaction between F0 difference and session was not significant [F (10, 40) = 0.39, p = 0.940]. Since there was no significant effect of session, the identification scores of one vowel in each of the pairs were also averaged across sessions for each listener. The identification scores [Fig. 3A] only significantly increased between the 0.5- and 1-semitone conditions [F (1, 4) = 11.15, p = 0.029].
A two-way repeated measures ANOVA was performed between F0 difference and percent identification scores of one or two vowels in the pair (Figs. 23). All scores were rationalized-arcsine transformed (Studebaker, 1985). The interaction between F0 difference and one or two vowel identification was significant [F (5, 20) = 27.85, p < 0.001]. At each F0 difference, the identification of two vowels was significantly poorer than the identification of one vowel (p ≤ 0.008). These statistical analyses confirm that F0 difference has a larger effect on identifying two vowels than on one vowel in the pair.
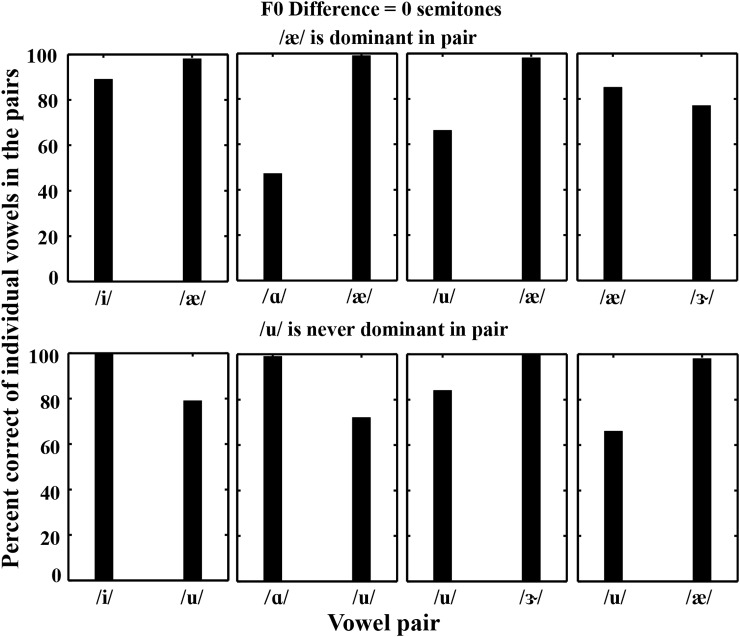
The patterns observed in identifying one vowel suggest that one of the two vowels was consistently “dominant” or most accurately identified. For the 0-semitone F0 difference condition (Fig. 4), there were two consistent observations: (1) /æ/ was the dominant vowel when present in a pair (top panels) and (2) in the presence of /u/, the other vowel was always dominant (bottom panels). These results suggest that without an F0 difference listeners might have taken advantage of relative differences in levels of formants between two vowels (Fig. 1). In contrast, there was much less difference in identification between the two vowels in each pair for the 4-semitone condition because the identification of the non-dominant vowel (e.g., /u/) improved considerably with respect to the 0-semitone condition. These results suggest that F0 difference was a contributing factor for identification of the non-dominant vowel in the pair, whereas the dominant vowel was typically identified well irrespective of the F0 difference.
Figure 4.
Two consistent differences in the identification of individual vowels in a pair were observed for the 0-semitone condition. Top: /æ/ was always the dominant vowel when present; bottom: /u/ was always the non-dominant vowel when present. Here, mixed and reversed-mixed vowel pairs were the same, hence the data corresponding to these pairs were averaged.
Effect of formant separation on F0 benefit of vowel pairs
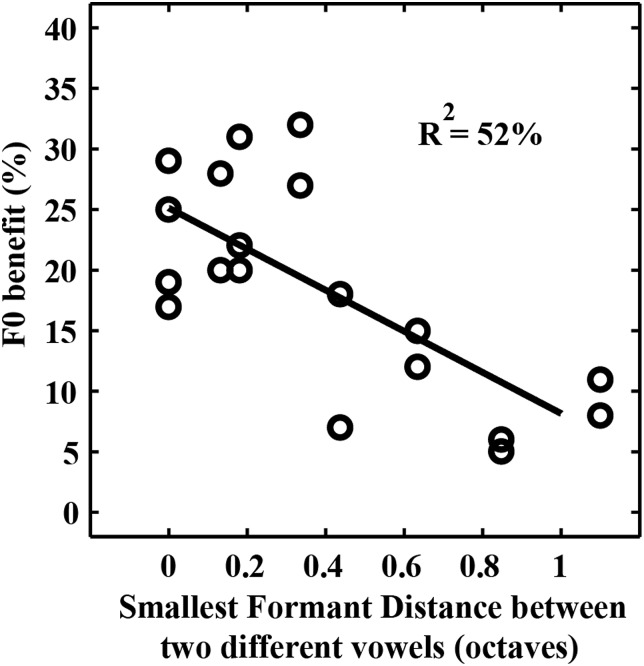
Consistent with previous studies (e.g., Scheffers, 1983a; Qin and Oxenham, 2005), our identification data revealed that the F0 benefit was larger when two vowels in the pair had similar first formants (e.g., /ɑ, æ/) or second formants (e.g., /ɑ, ɝ/) and smaller when two vowels in the pair had distinct first and second formants (e.g., /i, ɝ/ and /i, ɑ/). F0 benefit has been defined as the difference in identification scores between 4-semitone and 0-semitone conditions. Figure 5 shows the association between the smallest formant distance between two vowels in the pair and their F0 benefit. The formant distance (in octaves) between the first formant of one vowel (v1) and the first formant of the other vowel (v2) in the vowel pair (/v1, v2/) was log2 [F1(v1)/F1(v2)], where F1(v1) was the first formant of v1 and F1(v2) was the first formant of v2. There were four formant distances1 for each pair and the minimum of these distances was the smallest formant distance. In Fig. 5, a lower value for the smallest formant distance between the two vowels (i.e., the two vowels had similar formants) corresponded to a higher value for the F0 benefit, and vice versa. Linear regression analysis between the smallest formant distance and F0 benefit revealed that the slope was significantly different from zero and 52% of the variance in F0 benefit was explained by this simple formant-distance measure. The remaining variance may be explained by additional factors, such as the other formant distances or more generally the relative difference in the entire spectral envelopes between the two vowels (Fig. 1).
Figure 5.
Effect of smallest formant distance between two different vowels on their F0 benefit. Only the first and second formants of the vowels were considered, and identical vowels were not included. A lower value of the smallest distance corresponded to a higher value of F0 benefit. The difference in the identification scores between the 4- and 0-semitone conditions corresponds to the F0 benefit.
Vowel confusions
The criterion for analyzing a confusion at each F0 difference was that the mean error rate had to be ≥10% (as in Scheffers, 1983a), and at least three out of the five listeners had to make the confusion. To examine the confusions in detail, Table TABLE II. shows the mean confusion matrix for vowel pairs in the absence of an F0 difference for the five listeners. Because F0 for the two vowels was the same, the mixed and reverse-mixed vowel pairs were the same. Hence, the scores for these pairs were averaged. The following observations were made from the confusion matrix: (1) correct identification of both vowels (values along the diagonal) varied substantially with the vowel pairs, (2) most of the pairs produced a maximum of 1 or 2 confusions out of 15 responses, suggesting that listeners made actual confusions, rather than random guessing (Scheffers, 1983a), (3) sometimes /u/ was not identified in the pair when presented along with the other vowels (also seen in Fig. 4), perhaps due to the relatively low spectral envelope level beyond the first formant (>500 Hz, as seen in Fig. 1), (4) sometimes /u/ was mistakenly identified as one of the vowels in the pair when identical vowels (e.g., /ɑ, ɑ/) or vowel pairs with higher spectral envelope level (e.g., /ɑ, æ/) were presented, and (5) vowels that had similar formants or spectral envelopes were confused with one another (e.g., /ɑ/ and /æ/, /i/ and /u/, and /ɝ/ was confused with /ɑ/).
TABLE II.
Mean confusion matrix (15 × 15) for vowel pairs in the 0-semitone F0-difference condition. Rows correspond to the stimulus and columns correspond to the response. The number shown in each cell is the mean response percentage for each stimulus. Correct responses are in the diagonal cells. Overall percent correct identification was 73%. Confusions are the off-diagonal cells and are shown only if ≥10%. For this condition, the mixed and reversed-mixed vowel pairs are the same and thus the rows corresponding to these pairs were averaged.
| Response | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Identical vowel pairs | Mixed vowel pairs | ||||||||||||||
| Stimulus | i,i | ɑ,ɑ | u,u | æ,æ | ɝ,ɝ | i,ɑ | i,u | i,æ | i,ɝ | ɑ,u | ɑ,æ | ɑ,ɝ | u,æ | u,ɝ | æ,ɝ |
| i,i | 83 | 18 | |||||||||||||
| ɑ,ɑ | 73 | 17 | |||||||||||||
| u,u | 100 | ||||||||||||||
| æ,æ | 48 | 11 | 21 | 16 | |||||||||||
| ɝ,ɝ | 51 | 47 | |||||||||||||
| i,ɑ | 90 | ||||||||||||||
| i,u | 20 | 79 | |||||||||||||
| i,æ | 86 | ||||||||||||||
| i,ɝ | 94 | ||||||||||||||
| ɑ,u | 15 | 13 | 70 | ||||||||||||
| ɑ,æ | 24 | 44 | 16 | ||||||||||||
| ɑ,ɝ | 12 | 64 | |||||||||||||
| u,æ | 12 | 14 | 64 | ||||||||||||
| u,ɝ | 17 | 81 | |||||||||||||
| æ,ɝ | 14 | 11 | 63 | ||||||||||||
Generally, the confusions observed with 0-semitone differences were reduced with increasing F0 difference (see Chintanpalli, 2011 for details). For example, in the 4-semitone condition, the increase in vowel segregation resulted in improved identification of both vowels and fewer confusions. In fact, only two confusions were observed in the 4-semitone condition: /ɝ, ɝ/ was confused as /u, ɝ/ (error rate = 14%, down from 47% in the 0-semitone case, Table TABLE II.) and /ɑ, æ/ was confused as /æ, æ/ (error rate = 20%, down from 24% in Table TABLE II.). All other confusions observed in Table TABLE II. dropped below the 10% criterion in the 4-semitone condition. However, the two confusions mentioned above were still >10% suggesting that listeners might have to utilize cues other than F0 difference (e.g., derived from cognitive processing) to further reduce the error rate.
Our confusion-pattern analyses across the other F0-difference conditions (not shown, but see Chintanpalli, 2011 for details) revealed that the mixed and reverse-mixed pairs had mostly the same vowel confusions. This observation suggests that the similarity in formants (or spectral envelopes) of the two vowels was the primary factor in producing confusions, whereas the relative order of the individual-vowel F0s did not affect the confusions as much.
MODELING OF CONCURRENT VOWEL CONFUSIONS
Despite the suggestion from a temporally based F0-segregation model (Meddis and Hewitt, 1992) that F0 differences are the main factor contributing to the F0 benefit in concurrent vowel identification, the present and previous studies' data indicate that other factors such as spectral differences may contribute (e.g., Fig. 5). Thus, we sought to use the confusion patterns measured in the present study to test further several models of concurrent vowel identification. Based on the finding from Fig. 5 and previous studies that F0 benefit is influenced by spectral differences, we sought to initially determine whether spectral models were able to account for vowel confusions on their own, or whether the type of temporally based analysis used in the Meddis and Hewitt (1992) model was necessary to account for listener confusions. Because the numbers of confusions for the 4-semitone condition are so few, the F0 benefit is largely determined by the performance in the 0-semitone condition. Thus, the initial analyses were focused only on the 0-semitone condition. However, we also examined the performance of the full Meddis and Hewitt (1992) F0-based segregation algorithm as a function of F0 difference to test the hypothesis that if this model were a complete model of concurrent vowel identification, it should capture human listener confusions successfully at all F0 differences.
Computational auditory-nerve model
Though there are many computational models of the auditory periphery [see reviews by Lopez-Poveda (2005) and Heinz (2010)], the auditory-nerve (AN) model described by Zilany and Bruce (2007) was selected for various reasons. First, this phenomenological model represents an extension of several previous versions of the model, which have been extensively tested against neurophysiological responses from cats to both simple and complex stimuli, including pure tones, two-tone complexes, broadband noise, and vowels (e.g., Carney, 1993; Heinz et al., 2001; Zhang et al., 2001; Bruce et al., 2003; Tan and Carney, 2003; Zilany and Bruce, 2006, 2007). Second, the model captures many of the cochlear nonlinearities, including compression, suppression, broadened tuning and best-frequency shifts with increasing sound level. Tuning-curve parameters derived from this model (Chintanpalli and Heinz, 2007) were shown to match well with those derived from neurophysiological cat data (Miller et al., 1997). Third, the model captures the phase locking (or temporal response) phenomena of AN fibers.
Finally, the model captures many of the effects of outer- and inner-hair-cell damage on AN responses (Heinz, 2010), and thus will be useful for future studies designed to examine the effects of different types of sensorineural hearing loss on the factors underlying concurrent vowel identification (Chintanpalli, 2011).
The input to the model is a concurrent vowel waveform (scaled in Pascals) and the primary output is the time-varying discharge rate of a single AN fiber (in spikes/s) from a specific characteristic frequency (CF, the frequency at which the fiber responds to the lowest tone level). The model also provides intermediate outputs at the cochlear filtering and inner-hair-cell stages. The output of the “C1-filter” was used in the present study to examine the ability of cochlear excitation patterns across CF to account for the measured listener confusion patterns. This ability was quantitatively compared to a simple acoustic spectral pattern model and a neural temporal pattern model to examine the relative contributions of cochlear filtering and neural temporal processing. This AN model was designed and tested successfully for high spontaneous rate (SR = 50 spikes/s) fibers, hence these fibers are used. Similar results are expected for low-SR fibers because phase locking does not depend strongly on SR (Johnson, 1980).
F0-based segregation algorithm
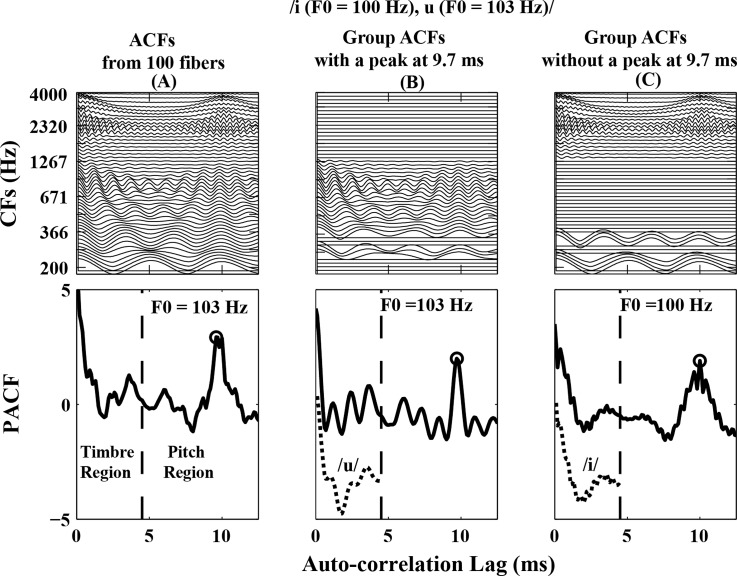
The Meddis and Hewitt (1992) F0-based segregation algorithm provides a good representation of the general effect of F0 difference on overall concurrent vowel identification for normal-hearing listeners. In the present study, the same F0-based segregation algorithm with a more modern AN model (Zilany and Bruce, 2006, 2007) was used. A vowel pair /i (F0 = 100 Hz), u (F0 = 103 Hz)/ was selected as an example (Fig. 6) of the model to illustrate the segregation stage (Meddis and Hewitt, 1992). The time-varying discharge rate responses from 100 AN fibers (CFs = [100–4000 Hz]) were obtained from the AN model (Zilany and Bruce, 2006, 2007) for this example pair. The auto-correlation function (ACF) was computed from the discharge rate to extract the periodicity information in each fiber response. The pooled ACF (PACF) was obtained by adding the 100 ACFs [top panel of Fig. 6A]. The PACF was divided into a temporal pitch (4.5–12.5 ms) and a timbre (0.1–4.5 ms) region. The dominant pitch was predicted as the inverse of the lag corresponding to the largest peak in the pitch region of the PACF and was equal to 103 Hz [i.e., the inverse of 9.7 ms, bottom panel of Fig. 6A]. For this vowel pair, the algorithm performed F0-based vowel segregation because less than 75% of ACFs showed a peak at the dominant pitch (or 9.7 ms). This segregation resulted in the division of the population of 100 fiber ACFs into two separate groups: ACFs that showed a peak at 9.7 ms [Fig. 6B] and ACFs that did not show a peak at 9.7 ms [Fig. 6C]. Two segregated PACFs were computed from these groups [bottom panels of Figs. 6B, 6C]. For vowel identification in each group, the timbre region of the segregated PACF was then compared with individual-vowel templates obtained from the timbre region of the PACFs from responses to the five single vowels.2 The best template match was taken as the vowel predicted by the model. For this example, /u/ with F0 = 103 Hz [bottom panel of Fig. 6B] and /i/ with F0 = 100 Hz [bottom panel of Fig. 6C] were predicted.
Figure 6.
Model predictions illustrating the F0-based segregation algorithm used for identifying the concurrent vowel /i(F0 = 100 Hz), u (F0 = 103 Hz)/. (A) Individual auto-correlation functions (ACFs) computed from 100 AN fibers. The ACFs were added together to obtain the pooled ACF (PACF, bottom panel). The vertical dashed line divides the timbre and pitch regions of the PACF. The highest peak in the pitch region of the PACF occurred at 9.7 ms. (B) All ACFs with a peak at 9.7 ms were grouped together. The model predicted the vowel /u/ and F0 = 103 Hz based on the best match to single-vowel templates (bottom panel). (C) Remaining ACFs (without a peak at 9.7 ms) were grouped together. The model predicted the other vowel as /i/ and F0 = 100 Hz (bottom panel). For visualization purposes, the timbre regions of the /u/ and /i/ templates (dotted lines) are shown in the respective bottom panels of (B) and (C), with an arbitrary vertical offset for clarity.
An alternative scenario can occur in the algorithm (not shown), where 75% or more of the fiber ACFs have a peak at the estimated dominant pitch (i.e., when there is not a significant representation of a second pitch and thus segregation is not justified). In this scenario, the algorithm performed the no-F0 segregation stage. In this stage, the model assumed that both vowels in the pair had the same F0 and the unsegregated PACF was created by including those ACFs that showed a peak at the estimated dominant pitch. For vowel identification, the timbre region of the unsegregated PACF was then compared with the templates corresponding to the timbre region of the PACFs from the five single vowels (as described above). The two best matches were predicted as the two different vowels in the pair (e.g., /i, u/), unless there was insufficient evidence for the presence of a second vowel. If the degree of the best template match (m1, representing the inverse Euclidian distance between the PACF and the template) was greater than the second best match (m2) by a criterion value, then the identical vowels in the pair (e.g., /i, i/) were predicted. Although the same F0-based segregation algorithm was used as in the Meddis and Hewitt (1992) study, slightly different parameters were necessary to produce a good fit to the overall percent correct identification of both vowels due to the different peripheral model used in the present study (Table TABLE III.).
TABLE III.
Differences in parameter values between the F0-based segregation algorithm of Meddis and Hewitt (1992) for concurrent vowel identification and the current implementation, both of which were based on a population of AN-fiber ACFs.
| Parameters | Meddis and Hewitt (1992) | Current implementation |
|---|---|---|
| ACF time constant (ms) | 10 | 20 |
| Vowel segregation criterion: maximum percentage of channel ACFs with dominant pitch | 80 | 75 |
| Single- versus double-vowel criterion in no-segregation case: Ratio of template matches (m1/m2) | 0.5 | 0.07 |
Stimuli and presentation level
The same set of 150 concurrent vowels was used in the modeling as were used in the behavioral experiments. The sound level of the individual vowels used in the modeling was 50 dB SPL, which was 15 dB below the sound level used in the behavioral experiments. This absolute difference in sound level between the two approaches is consistent with many previous AN-modeling studies that have predicted human performance from high-spontaneous-rate AN-fiber responses to complex speech-like stimuli (e.g., Swaminathan and Heinz, 2012). The high-SR fibers in this AN model had thresholds that were fit to the lowest observed AN-fiber thresholds in cat data (e.g., −5 dB SPL in the mid frequencies, with the AN-fiber threshold population having a ∼30–40 dB range above these lowest thresholds), see Miller et al., 1997; Bruce et al., 2003; Zilany and Bruce, 2006, 2007. Thus, the absolute sound levels at which envelope-modulation coding (e.g., to F0) begins to degrade (Joris and Yin, 1992) are quite low in the model fibers we used. However, the wide range of AN-fiber thresholds, along with efferent and long-duration dynamic range effects, suggest that there are very likely to be fibers in the AN population with essentially the same temporal coding properties at the behavioral sound level of 65 dB SPL. Thus, the 15-dB absolute sound-level difference between the two approaches is not expected to significantly limit the conclusions from the present study.
Results and discussion
Comparison of predicted confusion order based on acoustic spectral, cochlear excitation, and neural temporal patterns
The ability of spectral (acoustic and cochlear) and temporal (neural) models to predict the measured confusion patterns from human listeners were compared based on dissimilarity scores, computed across all vowel pairs. Comparisons were made for the 0-semitone condition, for which the largest number of confusions were made (Table TABLE II.). Dissimilarity scores for a given reference vowel pair were computed from the Euclidean distance3 between the spectral or temporal pattern of that pair and each of the 14 other vowel pairs separately. To facilitate quantitative comparisons across the different model types, for a given reference pair and model type each dissimilarity score was normalized by the maximum dissimilarity score across all vowel pairs.
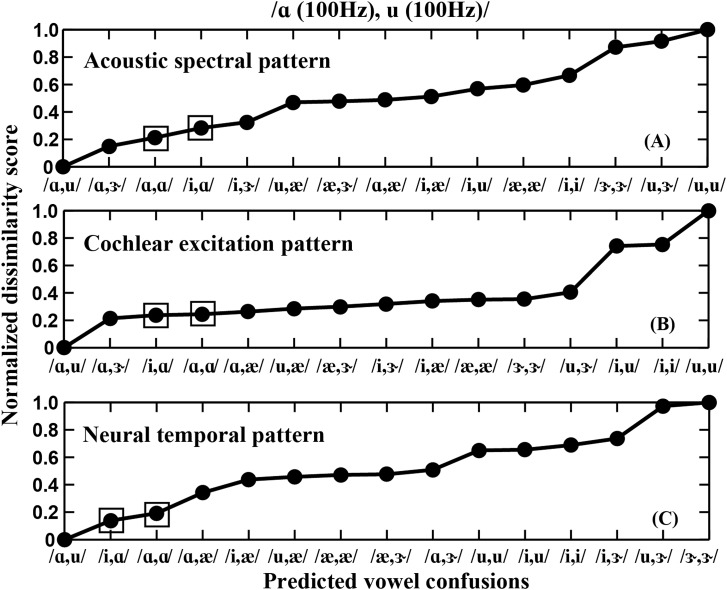
Figure 7A shows the acoustic spectral pattern dissimilarity scores for the example vowel pair /ɑ, u/ in ascending order. This vowel pair was selected because listeners sometimes could not identify /u/ when it was presented along with the other vowels (Fig. 4, Table TABLE II.). Lower dissimilarity scores suggest higher rates of acoustic confusions, and vice versa. Based on the degree of dissimilarity in spectral envelopes between the various vowel pairs, the acoustic spectral model predicted that /ɑ, u/ would be most easily confused with /ɑ, ɝ/, followed by /ɑ, ɑ/ and then /i, ɑ/ [Fig. 7A]. Although the vowel pairs /ɑ, ɑ/ and /i, ɑ/ were the same two pairs that humans listeners confused /ɑ, u/ with, the most-easily confused vowel pair based on this simple acoustic spectral model was /ɑ, ɝ/ that was not made by human listeners (Table TABLE II.). This suggests that had listeners relied solely on the acoustic spectral pattern to identify the concurrent vowel pair /ɑ, u/, a different pattern of confusions would have been observed.
Figure 7.
Predictions on the order of confusions based on spectral (acoustic and cochlear) and temporal (neural) analyses for the example vowel pair /ɑ (F0 = 100 Hz), u (F0 = 100 Hz)/. The alternative vowel pairs are ordered based on ascending dissimilarity score (i.e., decreasing confusability with the reference vowel pair). (A) Acoustic spectral pattern confusions. (B) Cochlear excitation pattern confusions. (C) Neural temporal pattern confusions. Square boxes denote the onlytwo confusions /ɑ, ɑ/ (15%) and /i,ɑ/(13%) made by listeners (Table TABLE II.). To facilitate comparison across models, all dissimilarity scores were normalized by the largest score across the 15 vowel pairs for each model type (i.e., within each panel).
To evaluate whether nonlinear cochlear tuning alters the spectral pattern in such a way as to improve the prediction of listener confusions, the same analyses were made using the cochlear-filter (C1-filter) output from the AN model. The cochlear excitation pattern dissimilarity score was computed based on the Euclidean distances between the C1-filter spectral patterns from the reference pair and each of the 14 other vowel pairs separately.4 Figure 7B shows the cochlear excitation pattern dissimilarity scores for /ɑ, u/ in ascending order. The first three predicted confusions based on the cochlear excitation pattern model were the same as those predicted from the acoustic spectral model. Similarly to the acoustic model, the two confusions made by the human listeners were predicted to be the second and third most likely confusions based on cochlear excitation model [Fig. 7B]. However, again the confusion that was predicted to be made most often based on cochlear excitation patterns was the vowel pair /ɑ, ɝ/, which was a confusion that was not made by human listeners. Furthermore, the dissimilarity scores among the first 11 confusions were quite similar to one another, suggesting similar degrees of confusions among a large set of vowel pairs. This prediction is in contrast to the consistently observed pattern of confusions among human listeners in which a maximum of one to three confusions were made for each vowel pair. Thus, both acoustic and cochlear spectral analyses predict confusion patterns for concurrent vowel identification with no F0 difference that do not fully account for human listener confusion patterns.
Figure 7C shows ascending dissimilarity scores computed based on neural temporal patterns for the same reference vowel pair /ɑ, u/. Comparison of these neural temporal analyses with the spectral analyses in Figs. 7A, 7B provide an indication of whether information derived from phase locking in AN fiber responses can provide a better account of listener confusion patterns than the simple spectral response analyses. To predict the order of neural temporal pattern based confusions for a given vowel pair, the Euclidean distances were computed between the timbre regions of the PACF (Sec. 3B) from that vowel pair and each of the other 14 vowel pairs separately. For the neural temporal model, the two most likely confusions predicted were /i, ɑ/ and /ɑ, ɑ/, which are the same two confusions made by the human listeners (Table TABLE II.). Furthermore, the remainder of the vowel pairs had dissimilarity scores that were a factor of 2 or more larger than the two most-likely predicted confusions. This pattern of results is consistent with the observation that human listeners did not make confusions other than the primary two vowel pairs for the reference vowel pair /ɑ, u/.
These three simple model analyses were also done for all vowel pairs, with similar results (not shown) obtained in each of the model analyses as were shown for the example reference vowel pair /ɑ, u/ (Fig. 7). Overall, the neural temporal model [Fig. 7C] appears better able to account for the listener confusion patterns than either of the spectrally based models [Figs. 7A, 7B]. Not only did the neural temporal model predict the two confusions made by listeners (as all models did), but it also predicted that no other confusions were likely to be made. In contrast, the spectral models predicted incorrectly that the most likely confusion was a confusion not made by human listeners. Thus, it appears that temporal analyses are required to account fully for the measured confusion patterns made by human listeners.
Model predictions of concurrent vowel identification using F0-based segregation algorithm
The Meddis and Hewitt (1992) F0-based segregation algorithm relies on the neural temporal analyses that were found in Fig. 7 to be beneficial in accounting for listener confusion patterns for the no-F0-difference condition in which the majority of confusions were observed. This model was originally shown to account for the gradual increase in concurrent-vowel identification as F0 difference increased by using these neural temporal analyses to first segregate the vowels and then also to identify the individual vowels. Here and in the following section, we evaluate in Fig. 8 whether this algorithm can also account for listener confusion patterns equally well as a function of F0 difference, as would be expected if this model is a complete model of concurrent vowel identification.
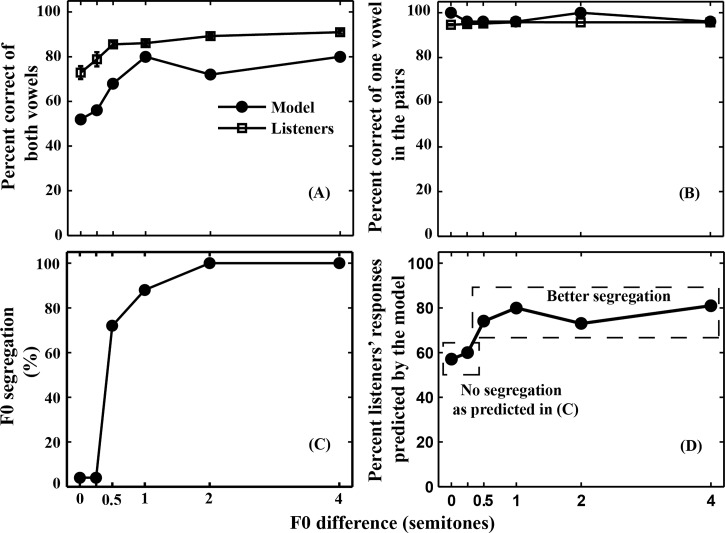
Figure 8.
Predicted effects of F0 difference on concurrent vowel identification using the segregation model. (A) Identification of both vowels. (B) Identification of at least one vowel. For comparison, the identification data from normal-hearing listeners [Figs. 2A, 3A] are included in (A) and (B). (C) Percentage of vowel pairs for which the model segregated the ACFs into two sets based on F0 differences. (D) Similarity scores between the model and listeners' data, indicating the percentage of human responses captured by the model. Normalization was used to overcome the upper limit on percentage match associated with the model's deterministic responses (see text for details).
In the model predictions, the percent correct identification of both vowels increased with F0 difference and then asymptoted at 1 semitone difference [Fig. 8A]. The model predicted a similar effect of F0 difference as observed in our listeners but had reduced overall scores. A very high identification of one vowel in each of the pairs was predicted [Fig. 8B], which matched well with the listeners' identification data.
Using the model, F0 segregation (i.e., vowel segregation using the 75% criterion, Table TABLE III.) was quantified for each pair at different semitone conditions. The ability to segregate two vowels (using F0 difference) was predicted to improve with increasing F0 difference and then to reach a maximum for F0 difference ≥2 semitones [Fig. 8C]. With no F0 segregation at 0 and 0.25 semitone differences, the identification scores were considerably higher than chance (1/15), suggesting that differences in vowels' formants and their levels were used as a significant cue for identification (Fig. 1). The sharp increase in F0 segregation from 0 to 1 semitones resulted in a modest ∼25% improvement in identification of both vowels [compare Figs. 8C, 8A]. Further improvement in F0 segregation for 2 and 4 semitone differences did not affect the identification scores. These quantitative comparisons revealed that the increase in identification scores can be partly, but not completely, attributed to improvement in F0 segregation.
Model predictions of listener confusions using F0-based segregation algorithm
Because the segregation model was entirely deterministic, the identification response was always the same for all repetitions of the same vowel pair. Hence, the performance of the model did not include the response variability observed in the listener data (e.g., Table TABLE II.). Thus, to provide a quantitative comparison between model and human confusions as a function of F0 difference, we computed a similarity score that was equal to the average (across all vowel pairs presented) of the human response percentage corresponding to each model response (e.g., from Table TABLE II.). Because the model only has a single response, the best possible performance of the model would be to predict the highest percentage response from the human data, which was generally less than 100% with a maximum value that depends on human performance. Thus, we normalized the metric by dividing each response percentage by the highest percentage human response for each vowel pair. This normalized metric thus would equal 100% if the model did as well as it possibly could by predicting the highest human response percentage for each vowel pair. The average similarity scores were computed across all vowel pairs at each F0 difference [Fig. 8D]. The unnormalized similarity metric (not shown) ranged from ∼40%–45% for the 0- and 0.25-semitone difference conditions to ∼60%–70% for the 0.5- and larger semitone difference conditions, which represent the percentage of human responses predicted by the model. The normalized metric shown in Fig. 8D (essentially representing the percentage of best possible performance of the model) also varied with F0 difference, ranging from ∼60% for the 0- and 0.25-semitone difference conditions to ∼80% for larger differences. The lower similarity scores for the 0- and 0.25-semitone conditions suggest that the model does not consistently account for the listener responses across F0-difference conditions, having the most difficulty in accounting for listener responses when there are minimal or no F0-difference cues [Fig. 8D]. Thus, although the F0-based segregation algorithm proposed by Meddis and Hewitt (1992) accounts for the pattern of increasing overall performance as F0-difference increases, it does not fully account for concurrent-vowel identification by human listeners when specific confusions are considered.
GENERAL DISCUSSION
The current study examined the effect of F0 difference on identification of concurrent vowels and confusions made by normal-hearing listeners. Consistent with other studies, the identification of both vowels increased with increasing F0 difference and then asymptoted at larger F0 differences. Our results revealed that the identification of one vowel in each of the pairs was largely independent of F0 difference and that the F0 difference was mainly required to identify the other vowel in the pair. Overall, a maximum of only one to three confusions were made for each vowel pair in the condition without F0-difference cues, and the percentage of each of these confusions decreased as F0-difference increased. The F0 benefit was found to vary across vowel pairs, and was inversely related (Fig. 5) to the smallest difference in formant frequencies between the individual vowel constituents of the vowel pair.
Although this and other evidence suggests that the spectral patterns of the concurrent vowels influence performance, simple modeling based on spectral and temporal patterns suggested that neural temporal analyses were needed to account better for the specific confusions made by listeners in the 0-semitone difference condition (Fig. 7). However, the model using a commonly accepted F0-based segregation algorithm (Meddis and Hewitt, 1992) was not able to fully account for the specific confusions made by our human listeners. Furthermore, the ability of this model to account for listener confusions varied as a function of F0 difference [Fig. 8D]. Thus, the results from the present study suggest that although neural temporal analyses are needed to account for human confusions, the commonly accepted model for concurrent vowel identification is incomplete and that F0-difference based segregation is not the only factor contributing to the gradual improvement in concurrent vowel identification as F0 difference increases.
Limitations in the present study
The F0-based segregation algorithm for concurrent vowels predicted similar trends in overall percent correct identification of both vowels and percent correct identification of one of the two vowels. However, the model performance in identifying both vowels was below that of our measured human performance [Fig. 8A]; although performance varies across studies and our model performance seems to be in line with some previous studies (e.g., Assmann and Summerfield, 1990). There are several possible explanations for this difference. The overall sound levels used in the present human and model data collection differed by 15 dB; however, as described above we do not expect this level difference to significantly limit the conclusions from the present study because of the range of fiber thresholds and types that have been reported in neurophysiological studies.
Perhaps more likely, listeners could have utilized some of the additional cues for identification of both vowels that were not included in the model, i.e., beyond the temporally based F0 and timbre differences between vowels. For example, although the simple spectral models considered here did not account for listener confusions as well as the temporally based neural model, it is possible that they could contribute to improved overall performance if they were used in addition to (instead of rather than) the temporal cues. The addition of such cues could improve performance in the no-F0-difference condition, where F0-differences are not available for segregation. Another possible reason for the high levels of performance in our human listeners is the use of feedback in both training and testing. It is possible that listeners learned to use somewhat subtle alternative cues that may be available for this closed-set task. Some of these cues could have been learned through neural plasticity and corticofugal effects from auditory cortex, which might be beneficial for attention (e.g., Giard et al., 1994). Similarly, most of the current AN models do not yet include the medial olivocochlear efferent effects, which have been shown to improve the neural coding of tones in the presence of background sounds (Kawase et al., 1993; Chintanpalli et al., 2012) and might therefore be relevant for the identification of concurrent vowels. Finally, it is also possible that phase-locking of AN fibers to concurrent vowels presented here can be transformed into a rate representation in inferior colliculus through mechanism not represented in the present modeling (e.g., Krishna and Semple, 2000; Nelson and Carney, 2004). Listeners may utilize these rate-based cues for the identification of both vowels; however, this needs to be investigated further to determine whether this central processing would improve performance over the temporally based performance at the level of the AN.
Another limitation is that the current modeling study has used the ACF extensively to predict the performance of concurrent vowels. However, it is still not know if the neural representations of the longer delays required for computing ACF exist in central auditory system. Nevertheless, the ACF models have accounted for many pitch-related phenomena as observed in listeners' data (e.g., Cariani and Delgutte, 1996).
Future model improvements
Listeners made minimal or no confusions at larger F0 differences between vowels but typically had one to two confusions at smaller F0 differences. The current model had greater difficulties in capturing the confusions made by listeners for 0- and 0.25-semitone difference conditions. This implies that the no-F0 segregation stage [Fig. 8C] of the Meddis and Hewitt model needs to be improved in order to account better for listener confusions. Beyond combining a spectrally based metric with the current temporally based metric as discussed above, one approach can be to estimate the unsegregated PACF by adding the ACFs from 100 AN fibers rather than only those ACFs that showed a peak at the dominant pitch. Further investigation is necessary to improve this stage and listeners' confusions appear to be a beneficial approach for its validation.
It would also be useful in future extensions to overcome the limitation in the present study that, in contrast to the listener data, the complete F0-based segregation model response to a given vowel pair was the same even with multiple repetitions (i.e., deterministic). The normalized similarity score metric [Fig. 8D] overcomes this issue to some extent, but yet is still limited in its ability to directly compare model and human confusions. Thus, a more thorough stochastic decision process that incorporates response variability in the predictions would allow for more direct comparisons between human and model responses.
Although a single AN model was used in the present study, it is likely that other physiologically realistic AN models would give similar results (e.g., models of Meddis and colleagues). In the latest version of the AN model used here, the strength of phase locking was improved due to the incorporation of new synaptic power-law dynamics (Zilany et al., 2009). However, even with this improvement, the basic properties of AN-fiber phase locking to vowel formants and F0s would remain the same, which forms the basis for the current conclusions. Thus, it is unlikely that the conclusions from the current study would be altered if a different AN model was used.
Future applications to sensorineural hearing loss
One benefit of using this line of AN models (Zilany and Bruce, 2007; Zilany et al., 2009) is that the functionality of the outer-hair-cells (OHCs) and inner-hair-cells (IHCs) can be adjusted by two model parameters (COHC and CIHC), which range from 1 (normal function) to 0 (complete hair-cell loss). This feature will be useful in predicting identification data related to sensorineural hearing loss (Chintanpalli, 2011).
Future work could include: (1) to investigate the effect of F0 differences on identification of both vowels, one vowel correct in the pairs, and confusions made by listeners with sensorineural hearing loss, and (2) to use the current model of concurrent vowels to gain more insight on the relative ability of OHC and IHC damage to predict the identification data and confusions from listeners with sensorineural hearing loss. This type of framework for this or other tasks might be beneficial in estimating the underlying configuration of OHC and IHC damage in individuals with hearing losses (e.g., Lopez-Poveda and Johannesen, 2012).
ACKNOWLEDGMENTS
This work was a part of the Ph.D. dissertation of A.C. at Purdue University. M.G.H. holds a joint faculty appointment in the Weldon School of Biomedical Engineering, Purdue University. We thank Judy R. Dubno, Jayne B. Ahlstrom, Christophe Micheyl, and Marjorie Leek for their invaluable comments and suggestions. Thanks to Fu-Shing Lee for his suggestions in statistical analyses. We would also like to thank all subjects who participated in this study. This research was supported by Purdue University and NIH-NIDCD (Grant No. R01-DC009838).
Portions of this research were presented at the 160th Acoustical Society of America Meeting, Baltimore, MD, April 2010.
Footnotes
The other three formant distances were log2[F1(v1)/F2(v2)], log2[F2(v1)/F1(v2)], and log2[F2(v1)/F2(v2)], where F2(v1) and F2(v2) were the second formants of v1 and v2, respectively. This analysis was limited to F1 and F2 of the two vowels.
The timbre region of the PACF from a single vowel was the average of the timbre regions of the same vowel presented in isolation with F0's 100, 101.5, 103, 106, 112, and 126 Hz.
Euclidean distance = Σ(x − y),2 where x and y were the spectral envelopes of two vowel pairs for the acoustic spectral pattern analysis. For the cochlear excitation pattern analysis, x and y were the C1-filter outputs across CF of the two vowel pairs. For the neural temporal pattern analysis, x and y were the timbre regions of the PACFs of the two vowel pairs.
The cochlear excitation pattern for each pair was predicted by computing the rms energy of the “C1filter” output at each of the 100 different CFs ([100–4000 Hz]) using the AN model (Zilany and Bruce, 2007). Overall, there were 15 different cochlear excitation patterns corresponding to different pairs in the no F0-difference condition.
References
- Arehart, K. H., King, C. A., and McLean-Mudgett, K. S. (1997). “ Role of fundamental frequency differences in the perceptual separation of competing vowel sounds by listeners with normal hearing and listeners with hearing loss,” J. Speech Lang. Hear. Res. 40, 1434–1444. [DOI] [PubMed] [Google Scholar]
- Arehart, K. H., Rossi-Katz, J., and Swensson-Prutsman, J. (2005). “ Double-vowel perception in listeners with cochlear hearing loss: differences in fundamental frequency, ear of presentation, and relative amplitude,” J. Speech Lang. Hear. Res. 48, 236–252. 10.1044/1092-4388(2005/017) [DOI] [PubMed] [Google Scholar]
- Assmann, P. F., and Paschall, D. D. (1998). “ Pitches of concurrent vowels,” J. Acoust. Soc. Am. 103, 1150–1160. 10.1121/1.421249 [DOI] [PubMed] [Google Scholar]
- Assmann, P. F., and Summerfield, Q. (1990). “ Modeling the perception of concurrent vowels: Vowels with different fundamental frequencies,” J. Acoust. Soc. Am. 88, 680–697. 10.1121/1.399772 [DOI] [PubMed] [Google Scholar]
- Assmann, P. F., and Summerfield, Q. (1994). “ The contribution of waveform interactions to the perception of concurrent vowels,” J. Acoust. Soc. Am. 95, 471–484. 10.1121/1.408342 [DOI] [PubMed] [Google Scholar]
- Bregman, A. S. (1990). Auditory Scene Analysis: The Perceptual Organization of Sound (MIT Press, Cambridge, MA: ), pp. 1–792. [Google Scholar]
- Brokx, J. P. L., and Nooteboom, S. G. (1982). “ Intonation and the perceptual separation of simultaneous voices,” J. Phonetics 10, 23–36. [Google Scholar]
- Bruce, I. C., Sachs, M. B., and Young, E. D. (2003). “ An auditory-periphery model of the effects of acoustic trauma on auditory nerve responses,” J. Acoust. Soc. Am. 113, 369–388. 10.1121/1.1519544 [DOI] [PubMed] [Google Scholar]
- Cariani, P. A., and Delgutte, B. (1996). “ Neural correlates of the pitch of complex tones. I. Pitch and pitch salience,” J Neurophysiol. 76, 1698–1716. [DOI] [PubMed] [Google Scholar]
- Carney, L. H. (1993). “ A model for the responses of low-frequency auditory-nerve fibers in cat,” J. Acoust. Soc. Am. 93, 401–417. 10.1121/1.405620 [DOI] [PubMed] [Google Scholar]
- Cherry, E. C. (1953). “ Some experiments on the recognition of speech in one and both ears,” J. Acoust. Soc. Am. 25, 957–959. [Google Scholar]
- Chintanpalli, A. (2011). “ Evaluating the neural basis for concurrent vowel identification in dry and reverberant conditions,” Ph.D. dissertation, Purdue University. [Google Scholar]
- Chintanpalli, A., and Heinz, M. G. (2007). “ The effect of auditory-nerve response variability on estimates of tuning curves,” J. Acoust. Soc. Am. 122, EL203–EL209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chintanpalli, A., Jennings, S. G., Heinz, M. G., and Strickland, E. A. (2012). “ Modeling the anti-masking effects of the olivocochlear reflex in auditory nerve responses to tones in sustained noise,” J. Assoc. Res. Otolaryngol. 13, 219–235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Culling, J. F., and Darwin, C. J. (1993). “ Perceptual separation of simultaneous vowels: within and across-formant grouping by F0,” J. Acoust. Soc. Am. 93, 3454–3467. 10.1121/1.405675 [DOI] [PubMed] [Google Scholar]
- Culling, J. F., and Darwin, C. J. (1994). “ Perceptual and computational separation of simultaneous vowels: Cues arising from low-frequency beating,” J. Acoust. Soc. Am. 95, 1559–1569. 10.1121/1.408543 [DOI] [PubMed] [Google Scholar]
- de Cheveigné, A. (1999). “ Waveform interactions and the segregation of concurrent vowels,” J. Acoust. Soc. Am. 106, 2959–2972. 10.1121/1.428115 [DOI] [PubMed] [Google Scholar]
- Giard, M. H., Collet, L., Bouchet, P., and Pernier, J. (1994). “ Auditory selective attention in the human cochlea,” Brain Res 633, 353–356. 10.1016/0006-8993(94)91561-X [DOI] [PubMed] [Google Scholar]
- Heinz, M. G. (2010). “ Computational modeling of sensorineural hearing loss,” in Computational Models of the Auditory System, edited by Meddis R., Lopez-Poveda E. A., Popper A. N., and Fay R. R. (Springer, New York: ), pp. 177–202. [Google Scholar]
- Heinz, M. G., Zhang, X., Bruce, I. C., and Carney, L. H. (2001). “ Auditory-nerve model for predicting performance limits of normal and impaired listeners,” ARLO 2, 91–96. 10.1121/1.1387155 [DOI] [Google Scholar]
- Johnson, D. H. (1980). “ The relationship between spike rate and synchrony in responses of auditory-nerve fibers to single tones,” J. Acoust. Soc. Am. 68, 1115–1122. 10.1121/1.384982 [DOI] [PubMed] [Google Scholar]
- Joris, P. X., and Yin, T. C. T. (1992). “ Responses to amplitude-modulated tones in the auditory nerve of the cat,” J. Acoust. Soc. Am. 91, 215–232. 10.1121/1.402757 [DOI] [PubMed] [Google Scholar]
- Kawase, T., Delgutte, B., and Liberman, M. C. (1993). “ Antimasking effects of the olivocochlear reflex. II. Enhancement of auditory-nerve response to masked tones,” J. Neurophysiol. 70, 2533–2549. [DOI] [PubMed] [Google Scholar]
- Klatt, D. H. (1980). “ Software for a cascade/parallel formant synthesizer,” J. Acoust. Soc. Am. 67, 971–995. 10.1121/1.383940 [DOI] [Google Scholar]
- Krishna, B. S., and Semple, M. N. (2000). “ Auditory temporal processing: responses to sinusoidally amplitude-modulated tones in the inferior colliculus,” J. Neurophysiol. 84, 255–273. [DOI] [PubMed] [Google Scholar]
- Larsen, E., Cedolin, L., and Delgutte, B. (2008). “ Pitch representations in the auditory nerve: Two concurrent complex tones,” J. Neurophysiol. 100, 1301–1319. 10.1152/jn.01361.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez-Poveda, E. A. (2005). “ Spectral processing by the peripheral auditory system: Facts and models,” Int. Rev. Neurobiol. 70, 7–48. 10.1016/S0074-7742(05)70001-5 [DOI] [PubMed] [Google Scholar]
- Lopez-Poveda, E. A., and Johannesen, P. T. (2012). “ Behavioral estimates of the contribution of inner and outer hair cell dysfunction to individualized audiometric loss,” J. Assoc. Res. Otolaryngol. 13, 485–504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meddis, R., and Hewitt, M. J. (1992). “ Modeling the identification of concurrent vowels with different fundamental frequencies,” J. Acoust. Soc. Am. 91, 233–245. 10.1121/1.402767 [DOI] [PubMed] [Google Scholar]
- Micheyl, C., and Oxenham, A. J. (2010). “ Pitch, harmonicity and concurrent sound segregation: Psychoacoustical and neurophysiological findings,” Hear. Res. 266, 36–51. 10.1016/j.heares.2009.09.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller, R. L., Schilling, J. R., Franck, K. R., and Young, E. D. (1997). “ Effects of acoustic trauma on the representation of the vowel /ε/ in cat auditory nerve fibers,” J. Acoust. Soc. Am. 101, 3602–3616. 10.1121/1.418321 [DOI] [PubMed] [Google Scholar]
- Nelson, P. C., and Carney, L. H. (2004). “ A phenomenological model of peripheral and central neural responses to amplitude-modulated tones,” J. Acoust. Soc. Am. 116, 2173–2186. 10.1121/1.1784442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer, A. R. (1992). “ Segregation of the responses to paired vowels in the auditory nerve of the guinea-pig using autocorrelation,” in The Auditory Processing of Speech: From Sounds to Words, edited by Schouten M. E. H. (Mouton de Gruyter, Berlin), pp. 115–124. [Google Scholar]
- Qin, M. K., and Oxenham, A. J. (2005). “ Effects of envelope-vocoder processing on F0 discrimination and concurrent-vowel identification,” Ear Hear. 26, 451–460. 10.1097/01.aud.0000179689.79868.06 [DOI] [PubMed] [Google Scholar]
- Scheffers, M. (1983a). “ Sifting vowels: Auditory pitch analysis and sound segregation,” Ph.D. dissertation, Groningen University, Groningen. [Google Scholar]
- Scheffers, M. T. (1983b). “ Simulation of auditory analysis of pitch: an elaboration on the DWS pitch meter,” J. Acoust. Soc. Am. 74, 1716–1725. 10.1121/1.390280 [DOI] [PubMed] [Google Scholar]
- Studebaker, G. A. (1985). “ A ‘rationalized’ arcsine transform,” J. Speech Hear. Res. 28, 455–462. [DOI] [PubMed] [Google Scholar]
- Summerfield, Q., and Assmann, P. F. (1991). “ Perception of concurrent vowels: Effects of harmonic misalignment and pitch-period asynchrony,” J. Acoust. Soc. Am. 89, 1364–1377. 10.1121/1.400659 [DOI] [PubMed] [Google Scholar]
- Summers, V., and Leek, M. R. (1998). “ F0 processing and the separation of competing speech signals by listeners with normal hearing and with hearing loss,” J. Speech Lang. Hear. Res. 41, 1294–1306. [DOI] [PubMed] [Google Scholar]
- Swaminathan, J., and Heinz, M. G. (2012). “ Psychophysiological analyses demonstrate the importance of neural envelope coding for speech perception in noise,” J. Neurosci. 32, 1747–1756. 10.1523/JNEUROSCI.4493-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan, Q., and Carney, L. H. (2003). “ A phenomenological model for the responses of auditory-nerve fibers. II. Nonlinear tuning with a frequency glide,” J. Acoust. Soc. Am. 114, 2007–2020. 10.1121/1.1608963 [DOI] [PubMed] [Google Scholar]
- Vongpaisal, T., and Pichora-Fuller, M. K. (2007). “ Effect of age on F0 difference limen and concurrent vowel identification,” J. Speech Lang. Hear. Res. 50, 1139–1156. 10.1044/1092-4388(2007/079) [DOI] [PubMed] [Google Scholar]
- Zhang, X., Heinz, M. G., Bruce, I. C., and Carney, L. H. (2001). “ A phenomenological model for the responses of auditory-nerve fibers: I. Nonlinear tuning with compression and suppression,” J. Acoust. Soc. Am. 109, 648–670. 10.1121/1.1336503 [DOI] [PubMed] [Google Scholar]
- Zilany, M. S., and Bruce, I. C. (2006). “ Modeling auditory-nerve responses for high sound pressure levels in the normal and impaired auditory periphery,” J. Acoust. Soc. Am. 120, 1446–1466. 10.1121/1.2225512 [DOI] [PubMed] [Google Scholar]
- Zilany, M. S., and Bruce, I. C. (2007). “ Representation of the vowel /ε/ in normal and impaired auditory nerve fibers: model predictions of responses in cats,” J. Acoust. Soc. Am. 122, 402–417. 10.1121/1.2735117 [DOI] [PubMed] [Google Scholar]
- Zilany, M. S., Bruce, I. C., Nelson, P. C., and Carney, L. H. (2009). “ A phenomenological model of the synapse between the inner hair cell and auditory nerve: Long-term adaptation with power-law dynamics,” J. Acoust. Soc. Am. 126, 2390–2412. 10.1121/1.3238250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwicker, U. T. (1984). “ Auditory recognition of diotic and dichotic vowel pairs,” Speech Commun. 3, 265–277. 10.1016/0167-6393(84)90023-2 [DOI] [Google Scholar]