The Effect of Through-Plane Motion on Left Ventricular Rotation: A Study Using Slice Following Harmonic Phase Imaging

Abstract

Non-invasive quantification of regional left ventricular (LV) rotation may improve understanding of cardiac function. Current methods employed to quantify rotation typically acquire data on a set of prescribed short-axis slices, neglecting effects due to through-plane myocardial motion. We combine principles of slice-following tagged imaging with harmonic phase analysis methods to account for through-plane motion in regional rotation measurements. We compare rotation and torsion measurements obtained using our method to those obtained from imaging datasets acquired without slice-following. Our results in normal volunteers demonstrate differences in the general trends of average and regional rotation-time plots in mid-basal slices, and of the rotation versus circumferential strain loops. We observe substantial errors in measured peak average rotation of the order of 58% for basal slices (due to change in the pattern of the curve), −6.6% for mid-ventricular slices, and −8.5% for apical slices; and an average error in base-to-apex torsion of 19% when through-plane motion is not considered. This study concludes that due to an inherent base-to-apex gradient in rotation that exists in the LV, accounting for through-plane motion is critical to the accuracy of LV rotation quantification.

INTRODUCTION

There is a growing renewed interest in the quantification of left ventricular (LV) rotation and torsion [1-3]. Studies have shown that these quantities play an important role in maintaining normal cardiac function [4]. The cardiac twisting motion during systole is not only responsible for the systolic contraction and ejection of blood from the chamber, but also responsible for the storage of potential energy within the myofibers [5-6]. This energy, released during ventricular diastolic untwisting, is then responsible for the creation of pressure gradients and suction within the left ventricular chamber which results in normal filling [7]. Therefore, abnormalities in cardiac rotation or torsion can lead to ejection and filling abnormalities.

Several studies have quantified rotation and torsion using magnetic resonance (MR) tissue tagging [8-10], Tissue Doppler Imaging (TDI) [11-12], and Speckle Tracking Echocardiography (STE) [13-16]. While rotation and torsion measurements produced by these methods have been cross-validated [11,15], some problems still exist in the measurement approaches. Current methods typically acquire short-axis slices at a fixed location, ignoring through-plane motion. It is well known that a base-to-apex rotation gradient exists in the LV. As a result, we hypothesize that accounting for through-plane motion is critical for accurate assessment of left ventricular rotation and torsion. Studies using STE and TDI have documented difficulty in measuring basal rotations due to susceptibility to data dropout/speckle loss as a result of through-plane motion [11,15]. Although signal loss is not encountered in MR imaging methods, fixing the imaged slice results in tissue contributions from above and/or below the imaged slice due to tissue displacement in the through-plane direction. This may result in apparent rotation values that are different from the actual experienced rotation. These limitations all play a significant role in inaccurate quantification of rotation and torsion. In contrast, MR imaging methods such as slice-following or navigator-based approaches, are available to track out-of-plane motion of 2D slices [17-19]. In this study, we apply the slice-following approach to MR tagged images and compare the rotation results obtained from these datasets to those obtained from conventional MR tagged images. The Harmonic Phase (HARP) analysis method [20] is employed to track the two-dimensional in-plane motion of myocardial points on the imaged slices, from which regional rotation and torsion are computed. In this paper, we refer to the combined slice-following imaging and HARP analysis approach as Slice Following HARP (SF-HARP) [21].

Using SF-HARP, the true two-dimensional projection of the three-dimensional motion of myocardial points on the imaged slice can be tracked. In this paper, we divide the myocardium into three layers — endocardial, midwall, and epicardial — and present the average rotation and torsion in stacks of short axis slices for each layer. We also segment each slice into four regions — anterior, lateral, inferior, and septal — and report average peak rotation and peak torsion in these regions. We also study the relationships between rotation and circumferential strain in the LV through the investigation of rotation versus circumferential strain loops. These loops are derived by plotting circumferential strain along the y-axis and rotation along the x-axis throughout the cardiac cycle. The characteristics of these loops offer unique insight into the role of each measurement during different periods of the cardiac cycle. All results obtained using SF-HARP in six normal volunteers is compared to corresponding results obtained using conventional MR tagging.

METHODS

MR Imaging Methods

All the experiments were performed on a 1.5 Tesla (T) Siemens Sonata scanner (Siemens Medical Solutions, Erlangen, Germany), equipped with gradient coils capable of imaging at 33 mT/m and with maximum slew rates of 100 T/m/s. This study was approved by the Institutional Review Board of Yale University and all six subjects [2 females, 4 males; age: 25.16 (7.13) (mean (SD)) years; height: 1.69 (0.09) m; weight: 67.81 (11.02) kg; heart rate: 65.16 (7.05) beats per minute with no prior diagnosis or symptoms of any heart disease] provided written informed consent. All datasets were obtained with the subject in the supine position on the MR scanner table. Six short axis slices covering base-to-apex of the LV were prescribed. The slices were evenly spaced with a gap of 1.4 mm in between. The center of the slice group was approximated to be the center of the LV. For each short axis slice, two sets of measurements were obtained: 1) conventional 1-1 spatial modulation of magnetization (SPAMM) tagged images [22] were acquired with tags oriented in horizontal and vertical directions. The imaging parameters were: field of view: 300×300, imaging matrix: 256×128, slice thickness: 7 mm, repetition time (TR)/echo time (TE): 36/4 ms, bandwidth: ±64 KHz, and tag separation:8 mm, incrementing train of imaging flip angles with final flip angle of 20°, image acquisition window within each cardiac cycle: 600 ms, and 2) 1-1 SPAMM tagged images with the slice-following scheme were acquired with tags oriented in horizontal and vertical directions. Using the slice-following scheme, thin short axis slices were tagged, while a large slab that always encompasses the moving tagged slice was imaged (See Fig. 1). For each tagging direction, two series of complimentarily signed tagged images (say, A and B) were sequentially acquired within the same breath-hold following the previously described complimentary SPAMM (CSPAMM) acquisition [23]. The imaging parameters used were identical to case 1 with the exception that the imaging matrix was 256×64, the tagged slice thickness was 7 mm, and the imaged slab thickness was increased to 18-20 mm. The SNR in slice following imaging is affected for two reasons: 1) no unexcited tissue moving into the image plane due to through-plane motion increasing the SNR. This effect worsens as one progresses through the cardiac cycle, and 2) subtraction of signal from the non-tagged portion of the imaged slab results in residual noise from these regions that increases overall noise in the image. This effect worsens as the ratio of slab thickness to tagged slice thickness increases. In our paper, the former effects were first reduced by employing an incrementing train of imaging flip angles to maintain constant SNR over all frames in the cardiac cycle as described in previous work [17]. Next, the slab thickness was chosen to be the smallest thickness that ensured the tagged slice (especially the most basal slice) always remains within the slab throughout the cardiac cycle (as observed by the absence of any signal drop-out during end-systole). The ratio of slab thickness to slice thickness was maintained constant across all slices to maintain consistent SNR for all slices. Previous work published report reliable tagging CNR over the entire cardiac cycle [18], and phantom validation of SF-HARP tracking results [21] for slab thickness to tagged slice thickness ratios upto 3.75. Here, we use ratios of the order of 2.5-2.85, to ensure that reliability in tracking results are maintained. For both, conventional 1-1 SPAMM, and slice-following 1-1 SPAMM, the horizontal and vertical tagging acquisitions were conducted separately. Grid tags were not employed to maximize SNR in the harmonic peak of interest and to minimize interference from other harmonic peaks. Both, conventional and slice-following datasets were acquired over two breath-held scans per slice, one for each tagging direction. Both CSPAMM acquisitions for the slice-following datasets were acquired within a single breath-hold by reducing the number of phase-encode lines to 64. This was found to be sufficient to cover the region of interest around the harmonic peak that was later extracted during post-processing as described in detail below. The acquisition time per breath-hold for both conventional and slice-following datasets was approximately 25 s.

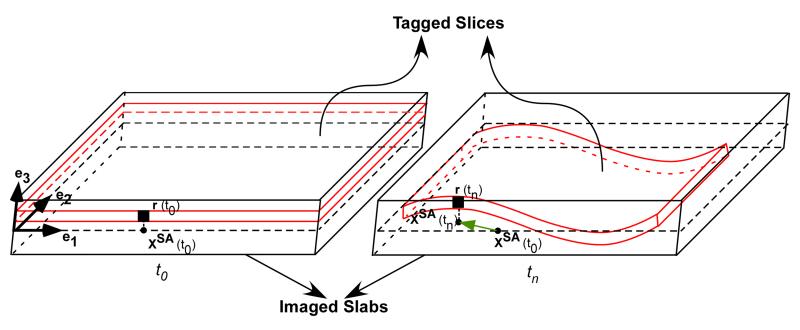
Fig. 1.

Combined slice-following scheme with CSPAMM results in the orthogonal projection of material points on the central cross sectional plane of the imaged slab. For example, at time t_0, the position of a selected material point on the tagged slice is denoted by r(t₀), and the projection of this point after the CSPAMM operation on the central cross-sectional short-axis plane is denoted by x^SA(t₀). At a later time t_n, the position of the same material point on the now deformed tagged slice is denoted by r(t_n). The deformed tagged slice continues to remain within the larger imaged slab, and the projection of the material point r(t_n) after the CSPAMM operation on the central cross-sectional plane is denoted by x^SA(t_n). Using HARP 2D tracking we can now track the true two dimensional displacement vector from x^SA(t₀) to x^SA(t_n).

HARP Analysis

Both sets of data (conventional tagging and slice-following tagging) were analyzed using HARP methodology with matched image analysis parameters. For the slice-following tagged images, the complex CSPAMM subtraction operation A-B was first applied to guarantee that the residual signal arises from the tagged slice alone, eliminating signal from untagged portions of the imaged slab. The resultant CSPAMM images was used for subsequent HARP analysis. For HARP analysis, one of the harmonic peaks obtained from the Fourier transform of the tagged images (for both conventional and post-processed slice-following images) was isolated using flat-topped circular band-pass filters of radius 28 pixels with Gaussian boundaries of width 4 pixels (total filter bandwidth=64 pixels). The isolated peaks were zero-padded to image size 256×256 and reconstructed to obtain a series of (complex valued) harmonic images. As per calculations described in [24], the HARP filter size chosen provides a dynamic range in strain measurements between −76% to 76% strain, which is well within the normal range of expected strain. As a result, good sampling of the tagging modulation function was achieved and the interpolation function (due to zero padding) enabled reliable reconstruction of the underlying harmonic phase function. With the imaging parameters used, the HARP filter size selected provides an underlying in-plane strain resolution of around 4.5mm × 4.5mm, which provides reasonable transmural sampling of the strain function in normal volunteers. Larger filter sizes may be required in patient studies with thin myocardial walls. The 2-D harmonic phase values, obtained from two series of orthogonally tagged harmonic images were then tracked to yield 2-D pathlines (trajectories) of selected material points on the image plane. In-house software originally developed at Johns Hopkins University [19], and later modified at Yale University was used for analysis in this paper.

SF-HARP

For the slice-following images, a material point, for example, located at a three-dimensional position r(t₀) = r₁(t₀)e₁ + r₂(t₀)e₂ + r₃(t₀)e₃ on a tag plane corresponding to a short-axis slice was considered (see Fig. 1), where (e₁, e₂, e₃) are the three identity vectors that define the 3-D orthonormal frame, and (e₁, e₂) define the short axis plane. At any later time t_n, the point r(t_n) lies on the deformed short-axis tag plane. The complex CSPAMM subtraction operation orthogonally projects this material point onto the central cross-sectional plane of the short-axis slab to give position vectors x^SA(t₀)=(r₁(t₀), r₂(t₀)) and x^SA(t_n)=(r₁(t_n), r₂(t_n)) on the resultant image at times t₀ and t_n respectively. Since the 2D harmonic phase of a given material point is preserved, the HARP analysis method will automatically track the displacement (r₁(t_n)- r₁(t₀), r₂(t_n)- r₂(t₀)) of material points from x^SA(t₀) to x^SA(t_n). Thus, the true 2D displacement trajectory is obtained when slice-following is employed. In contrast, HARP analysis of conventional tagged images tracks the 2D harmonic phase of a material point to another point in the neighborhood with the same 2D harmonic phase. This point may or may not be the same material point due to through-plane motion.

Image Analysis

Rotation Quantification

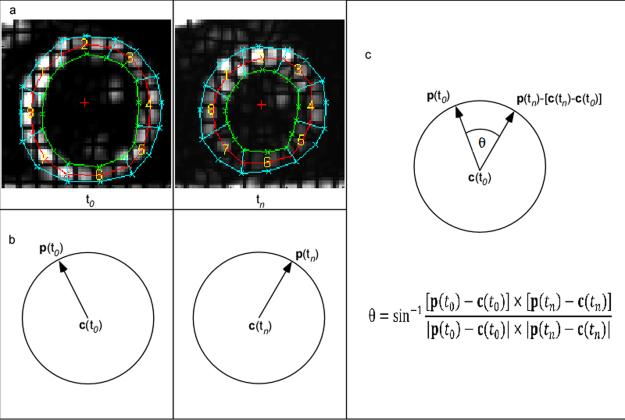
Rotation of a given material point on the image plane at any selected time point was calculated as the angle of rotation about the center of rotation with respect to a reference time frame. A user-defined mesh with three layers (endocardial, mid-wall, and epicardial layers) and eight regions was superimposed on the myocardium at the first time frame. The mesh was defined by 48 material points. Using HARP analysis, these material points defining the mesh were tracked in time thus automatically deforming the mesh. The center of rotation at any given time point was then defined as the center of mass of the material points defining the mesh at that given time point. Position vectors of all material points defining the mesh with respect to the center of mass were created at each time point t_n. These vectors were then translated to the reference frame by taking into account the change in the center of mass in order to calculate rotation (see Fig. 2)[5]. Theta was calculated for all octants of the imposed mesh and each myocardial layer. Average rotation of points lying on these three layers was computed for each slice. The rotation of material points was calculated using the following formula:

$$\text{Rotation}\left(\theta \right)={\sin }^{-1}\frac{\left[\mathbf{p}\right(t_0)-\mathbf{c}(t_0\left)\right]\times \left[\mathbf{p}\right(t_n)-\mathbf{c}(t_n\left)\right]}{\mid \mathbf{p}\left(t_0\right)-\mathbf{c}\left(t_0\right)\mid \mid \mathbf{p}\left(t_n\right)-\mathbf{c}\left(t_n\right)\mid }$$

Where p(t₀) and p(t_n) represent the 2D positions of a material point at the reference and current time frames respectively, and c(t₀) and c(t_n) are the 2D positions of the center of mass at the reference (the first time frame is selected as the reference time frame as minimal rotation has occurred at this time point) and current time points respectively. Positive rotation corresponds to clockwise rotation, while negative rotation corresponds to anti-clockwise rotation. A demonstration of the rotation calculation is shown in Fig. 2. In addition to computing average rotation of a given slice for each myocardial layer, average myocardial rotation on a regional basis for each slice was also computed. Four regions in specific were defined for each slice: lateral, inferior, septal, and anterior regions.

Fig. 2.

HARP Methodology / Rotation Calculation (a) All points on the mesh are tracked over all time frames. (b) For each point on the mesh, position vectors are constructed with respect to the center of mass. (c) Points at time t_n are translated so that the center is matched to the reference center, and the angle between new position vector p(t_n) at current time t_n and reference position vector p(t₀) at reference time t₀ is computed as the rotation angle θ. Rotation is then averaged for user-defined regions.

Torsion Quantification

As described in [8], torsion was defined as the circumferential-longitudinal shear angle in degrees that takes into account both, the length and the radius of the heart. Torsion was calculated for the base-to-apex, base-to-mid, and mid-to-apex regions of the LV. For each measurement, the average torsion in endo, mid, and epi regions were calculated. Average segmental torsion values were also calculated for lateral, inferior, septal, and anterior regions. Previous rotation measurements were used to compute torsion. Choice of apical, mid, and basal slices remained consistent over all datasets. The difference in rotation between a selected pair of slices was then computed. Radial lengths of all selected material points were measured for each frame for a given region or myocardial layer. For each selected slice, the average radial length of the reference and current frame was computed. The averaged radial lengths for each selected pair of slices were further averaged. Torsion was finally calculated by multiplying the difference in rotations between the selected pair of slices with average radial length of the pair of slices divided by the distance between the two slices. For example, base-to-apex torsion for the epicardial layer was calculated as follows:

$$\begin{array}{cc}\hfill & {\mathrm{d}}_{(\text{base-apex},\text{epicardial})}=\frac{{\left[{\mathrm{d}}_{(t_0,\mathit{epicardial})}+{\mathrm{d}}_{(t_n,\mathit{epicardial})}\right]}_{\mathit{apex}}+{\left[{\mathrm{d}}_{(t_0,\mathit{epicardial})}+{\mathrm{d}}_{(t_n,\mathit{epicardial})}\right]}_{\mathit{base}}}{4}\hfill \\ \hfill & \text{Torsion}\left({\Phi }_{\text{base-apex},\text{epicardial}}\right)=\frac{[{\mathrm{d}}_{(\mathrm{base}-\mathrm{apex},\mathit{epicardial})}\ast [{\theta }_{(\text{apex},\text{epicardial})}-{\theta }_{(\text{base},\text{epicardial})}\left]\right]}{L}\hfill \end{array}$$

where d_{(base-apex, epicardial)} represents the average radial epicardial length of the apical and basal slices, d_{(t0, epicardial)} and d_{(tn, epicardial)} represent the average radial length of material points defined in the epicardial layer at reference time frame t₀ and current time frame t_n respectively, θ_{(apex, epicardial)} and θ_{(base, epicardial)} represent the average epicardial rotations computed for the apical and basal slices respectively, and L represents the longitudinal distance between the selected apical and basal slice.

Circumferential Strain versus Rotation Loops

In order to examine the relationships between volumetric changes in the LV and ventricular rotation, we plotted average circumferential strain versus average rotation for a given slice. The average Lagrangian circumferential strain for each slice was computed based on the identical mesh used for rotation calculations. Lagrangian circumferential strain between two material points (consecutive material points on the mesh for a given myocardial layer were selected for these computations) was defined as the ratio of the change in circumferential distance between those two points with respect to a reference time frame and the distance between those two points at the reference time frame. The average Lagrangian strain between all points on each layer was computed, and the Lagrangian strain for the three layers was further averaged to compute average Lagrangian strain for each slice. This average strain value was then plotted against the average rotation value obtained for that slice.

Inter-Subject Analysis

All data analysis described above was conducted in six volunteers for six slices using the slice following scheme, and using conventional tagging sequences. To account for variability in heart-rate between volunteers, all rotation and torsion measurements were temporally normalized to a heart rate of 60 beats per minute (bpm). This was done by temporally scaling the resultant rotation and torsion curves by either appropriately squeezing (for heart rates <60 bpm) or stretching (for heart rates >60 bpm) the data curves using a uniform linear temporal scaling factor (=current heart-rate/60 bpm). Once the curves were temporally scaled and re-sampled, the mean and standard deviation of all rotation, and torsion measurements at each re-sampled time point were computed for all six volunteers.

Intra-Subject Analysis

Repeated image-analysis was also performed on a single volunteer to evaluate intra-observer variability due to image analysis. The manual steps involved during HARP image analysis typically includes definition of a filter size, and definition of the mesh applied on the LV. In view of this, repeated analysis was conducted for five filter sizes. For each filter size, repeated analysis was further conducted five times, each with a newly defined mesh.

RESULTS

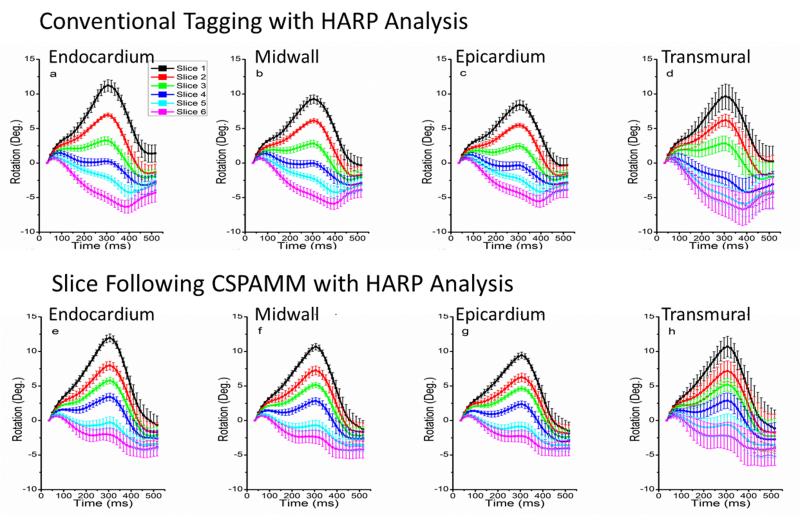
All graphs depict temporally normalized data averaged over all six volunteers. Fig. 3 illustrates the mean rotation curves for six slices from base to apex using conventional tagging techniques (row 1) and SF-HARP (row 2). Mean rotation curves are plotted for each myocardial layer (endocardium (column 1), mid-wall (column 2) and epicardium (column 3)) and for the entire slice (column 4). While the rotation, as expected, gradually shifts from a counter-clockwise to a clockwise rotation, the general trend of the curves in the two rows differ for mid-basal and basal regions. The rotation curves all appear to have a peak that occurs at the same time instant (around 300ms on the normalized time scale or 30% of cardiac cycle) in the cardiac cycle over all slices for SF-HARP. The curves obtained using conventional tagging, however, appear to flip over and have a shifted peak at around 400ms for mid-basal and basal slices. This is due to the fact that tissue from above the prescribed slice enters the imaged plane during mid-late systole. As a result, the curve represents a mixed-tissue response. From the curves obtained using SF-HARP, we observe that the peak at 300ms becomes smaller as you go from apex to base. As tissue from more basal regions move into the imaged slice in the conventional tagging datasets, this peak at 300ms is further suppressed, resulting in the appearance of a single negative shifted peak at 400ms.

Fig. 3.

Graphs of LV regional rotation using conventional tagging (row 1) and SF-HARP tagging methods (row2). Average rotation for endocardial (a&e), mid-wall (b&f), epicardial (c&g) layers, and average of all three layers (d&h) are presented. Slice 1 represents the most apical slice where-as slice 6 is the most basal slice. Error bars denote the standard deviation within the volunteer population.

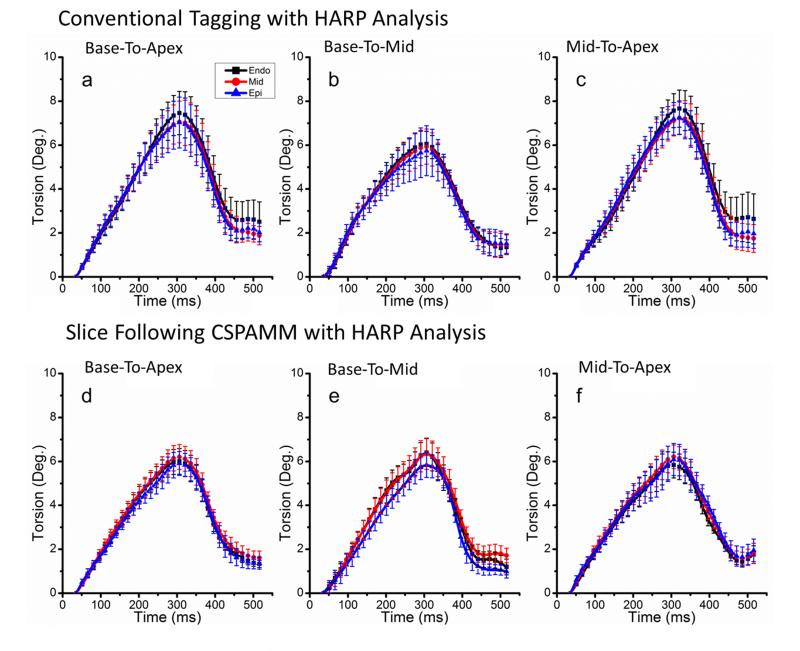
Fig. 4 demonstrates the results of average base-to-apex (column 1), base-to-mid (column 2) and mid-apex (column 3) torsion measurements for each layer obtained using conventional tagging (row 1) and SF-HARP (row 2). Similar to average rotation curves, peak average torsion occurs around 300ms. While the trends of the curves remain consistent between techniques, the peak torsion is reduced when using SF-HARP, especially for the base-to-apex and mid-to-apex measurements. Results of the averaged peak rotation (mean±SD for six volunteers) for the apical, mid and basal slices and torsion for each of the three myocardial layers are shown in Table 1 of the supplementary results (available online). While apical and mid rotations are similar for both techniques, the peak basal rotations are much higher (statistically significant at the p<0.01 level) when through-plane motion is not taken into consideration. This is mainly a result of the single shifted peak with a higher negative rotation observed at around 400ms in these curves. The base-to-apex and mid-to-apex torsion values are also overestimated (statistically significant at the p<0.2 level) when through-plane motion is ignored.

Fig. 4.

Graphs of average LV torsion of myocardial layers using conventional tagging (row1) and SF-HARP (row 2) methods. LV torsion for (a & d) base-to-apex, (b & e) base-to-mid, and (c & f) mid-to-apex regions are presented.

Table 2 of the supplementary results (available online) includes the peak rotations and torsions for each segmented region. Statistically significant differences are once again observed in peak basal rotation and base-apex torsion for all segmented regions. With SF-HARP, a consistent pattern begins to emerge between segments with the inferior segments exhibiting maximum rotation and torsion, and the anterior segments exhibiting minimum rotation and torsion. Accounting for through-plane motion may be important to highlight these differences between segments as each segment experiences a different degree of through-plane motion.

The mean±standard deviation in peak average rotation obtained from the repeated intrasubject image analysis is reported in Table 3 of the supplementary results (available online). The peak rotation values are computed for the endocardial, mid-wall and epicardial layers in an apical slice (acquired using SF-HARP) for each filter size and for overall measurements. We find that for a selected filter size, the standard deviations in measurements during repeated analysis were nearly 14-15 times lower, indicating that the differences observed in the results are mainly due to inter-subject variability or through-plane effects. For all analysis in the paper, we used a fixed filter radius of 32.

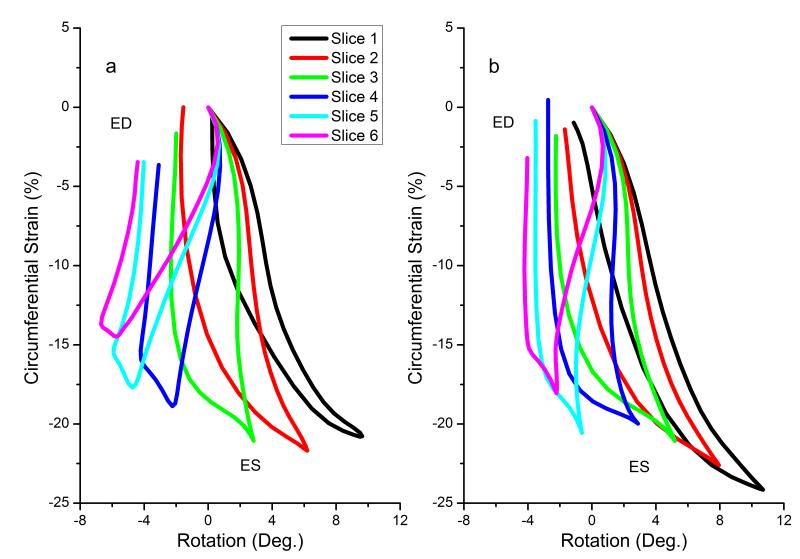
Fig. 5 shows loops of rotation versus circumferential strain for six slices using both techniques. We find that these loops resemble a typical non-linear magnetic hysteresis loop. A characteristic feature is observed during end systole (more prominent in apical and mid-ventricular slices) and early diastole. During these time periods, large changes in rotation (late twist and early untwist) occur with smaller corresponding change in circumferential strain. In contrast, during mid-late diastole, there are large changes in circumferential strain with small corresponding change in rotation (more prominent in mid-ventricular and basal slices). Differences in behavior of these loops between techniques are observed. The span of rotation values from base to apex is larger when using conventional tagging as opposed to SF-HARP. Thus, ignoring through-plane motion also alters the relative understanding between volumetric changes and rotation in the heart.

Fig. 5.

Loops of average rotation versus average circumferential shortening for (a) conventional tagging, and (b) SF-HARP methods. Slice 1 represents the most apical slice whereas slice 6 is the most basal slice. ES, End Systole; ED, End Diastole

DISCUSSION

Through this study, we have demonstrated that through-plane motion plays a significant role in the quantification of LV rotation and torsion, especially in regions close to the base. Our results in Fig. 3 and Table 1 (supplementary results) demonstrate difference in the temporal behavior of mid-basal and basal rotation-time curves with resulting significant differences in quantification of peak rotation in these slices. Myocardial tissue above the prescribed basal slice enters the fixed imaging slice plane during systole and leaves the slice plane during diastole. As a result, the rotation-time curve obtained using conventional tagging methods represents a mixed tissue temporal response where at early and late time points the rotation computed is for tissue at the prescribed basal slice and at other time points are from tissue regions above it. From the SF-HARP curves, the peak observed at 300ms is large in apical regions, and becomes smaller as you move to the base. We also observe that even at 400ms, the apical regions continue to have higher rotation values compared to basal regions, where a negative peak is observed around this time point. This feature observed in the rotation curves may be dictated by a need to maintain a certain fixed base-to-apex gradient in rotation to create the necessary LV pressure gradients required for normal LV filling during diastole. The relative base-to-apex gradient is maximum around 300ms, and decreases as we proceed further into diastole. After 400ms, the filling is nearly complete and the curves all begin to approach zero rotation. With the introduction of tissue from more basal regions in conventional tagging datasets during systole, the peak at 300ms is smaller (or more negative) as there is increased tissue contribution from regions above. As a result, one observes the disappearance of the peak at 300ms and the appearance of a single negative shifted peak at 400ms when conventional tagging is employed. Thus, the mixed tissue rotation curve appears to have a false delayed negative peak 100ms after the expected peak. This delayed basal peak was also observed in previous studies using the conventional tagging approach [8-10]. The apical curves maintain their shape. Although, the magnitude of peak rotations are under-estimated when through-plane motion is not taken into consideration, they are not statistically significant. Thus, large through-plane motion in the mid-basal and basal regions is particularly sensitive to significant observed differences in peak rotation and torsion measurements.

Recent studies report the significance of quantifying base-to-apex torsion to evaluate abnormal left ventricular function in several patient groups such as mitral regurgitation [25-27], cardiomyopathies [28-30], and aortic stenosis [31]. These studies rely on risk-stratification based on torsion quantification. Our results demonstrate that although the patterns of torsion curves are similar (i.e. relative rotation values using conventional tagging and SF-HARP are similar), the magnitude of base-to-apex torsion is overestimated when through-plane motion is not considered. Further, we expect that the degree of overestimation will vary depending on the position of the slice selected, and the amount of through-plane motion experienced. In patients, where through-plane motion may also be independently and regionally altered due to underlying disease, the amount of through-plane motion and its subsequent effect on rotation quantification will unpredictably vary between regions of a given slice and/or between slices, resulting in observed alterations in torsion measurements that do not solely reflect underlying LV rotation dysfunction. Thus, accounting for through-plane motion may be important in LV rotation and torsion quantification.

We present loops of rotation (or twist) versus circumferential strain. These loops provide unique insight into the relationships between volumetric changes and twisting motion in the heart. During systole, volumetric contraction (and circumferential shortening) occurs as blood is pushed out of the heart. We observed that peak circumferential shortening is highest in the most apical slice and lowest in the most basal slice. This circumferential shortening is accompanied by a more-or-less linear change in rotation as the heart twists storing potential energy. This change in rotation during systole is positive for the apical slices and negative for the basal slices. During early diastole, this potential energy is first released through a large untwisting motion and has been shown to be responsible for the creation of pressure gradients within the heart, which aids rapid filling. Interestingly, minimal change in volume occurs during early diastole. During mid-late diastole, however, rapid filling ensues resulting in the rush of blood into the ventricle causing large volumetric expansion (and circumferential expansion) with minimal change in rotation. These inter-relationships between strain and rotation, as observed through these loops, may be significant in diagnosis of various disease states.

Limitations

We present SF-HARP, a combination of slice-following imaging and HARP displacement tracking methods to compensate for through-plane motion effects in our rotation measurements. While other techniques such as navigator-based slice tracking approaches could be alternatively employed, we selected the slice-following approach due to its reproducibility and the direct coupling between the imaging approach and the image analysis methods. Our rotation results match closely with a previous published study using slice-following and HARP [32]. Although we have compared conventional tagging (and not CSPAMM) to CSPAMM with slice following, the differences observed in our results are mainly due to through-plane effects. This has been ensured by 1) selecting identical HARP filters during post-processing, and 2) minimizing interference effects from the dc peak through choice of filter size and shape and selection of a small tag separation of 7mm. For this study, we did not focus on high spatial resolution. The spatial resolution can be improved further by adopting the CANSEL approach [33] with slice-following or the ZHARP approach [34] to eliminate the complimentary harmonic peak, thus allowing the use of large HARP filter bandwidths, improving spatial resolution. Another limitation of this work is that a sparse collection of mesh points were used to compute strains and rotation measurements in regions. This can also be extended to a dense collection of points in future studies, but we do not expect this to change the results observed in this paper. We extracted a single harmonic peak for displacement analysis. In the future, SNR can be further improved by combining the harmonic phase images obtained from each of the two harmonic peaks [34]

CONCLUSION

Rotation and torsion are sensitive to through-plane motion effects. We observe changes in not only the trend followed by rotation curves (specifically in the mid-basal and basal slices), but also significant differences in computed peak rotation and torsion in the LV when through-plane motion is taken into account. This is especially evident in relation to basal regions (peak basal rotation and base-to-apex torsion) where maximum through-plane motion occurs.