Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Oct 28;3:3060. doi: 10.1038/srep03060

Demonstration of surface transport in a hybrid Bi2Se3/Bi2Te3 heterostructure

Yanfei Zhao 1,6, Cui-Zu Chang 2,3,6, Ying Jiang 4, Ashley DaSilva 5, Yi Sun 1, Huichao Wang 1, Ying Xing 1, Yong Wang 4, Ke He 2,b, Xucun Ma 2, Qi-Kun Xue 2,3, Jian Wang 1,a
PMCID: PMC3808819  PMID: 24162440

Abstract

In spite of much work on topological insulators (TIs), systematic experiments for TI/TI heterostructures remain absent. We grow a high quality heterostructure containing single quintuple layer (QL) of Bi2Se3 on 19 QLs of Bi2Te3 and compare its transport properties with 20 QLs Bi2Se3 and 20 QLs Bi2Te3. All three films are grown on insulating sapphire (0001) substrates by molecular beam epitaxy (MBE). In situ angle-resolved photoemission spectroscopy (ARPES) provides direct evidence that the surface state of 1 QL Bi2Se3/19 QLs Bi2Te3 heterostructure is similar to the surface state of the 20 QLs Bi2Se3 and different with that of the 20 QLs Bi2Te3. In ex situ transport measurements, the observed linear magnetoresistance (MR) and weak antilocalization (WAL) of the hybrid heterostructure are similar to that of the pure Bi2Se3 film and not the Bi2Te3 film. This suggests that the single Bi2Se3 layer on top of 19 QLs Bi2Te3 dominates its transport properties.

Three dimensional (3D) TIs are band insulators with gapless linear energy dispersion surface states1,2. Bi2Se3, Bi2Te3 and Sb2Te3 are confirmed as typical 3D TIs due to their simple single surface Dirac cone and relatively large bulk energy gap3,4. These materials provide the possibility for the observation of novel phenomena, including Majorana fermions5, magneto-electric effect6,7, and quantum anomalous Hall effect8,9, as well as the potential applications in quantum computation10. We know that semiconductor heterostructure consists of materials with different band structures and exhibits interesting quantum behaviors, such as quantum Hall effect11 and fractional quantum Hall effect in GaAs/AlxGa1−xAs heterostructures12. Recently, normal band insulator-3D TI or semimetal-3D TI heterostructures, such as Sb2Se3-Bi2Se313 and Bi-Bi2Se3 (Bi2Te3) heterostrctures14,15, have attracted much interest since the interface offers a new platform to study topological phase. However, up to now few experiments have been carried on the heterostructure of two different TIs. According to TI band theory, the existence of gapless surface state is due to the topological invariant change in the interface of trivial and non-trivial insulators1. As the ARPES measurements reported before16, when the thickness of Bi2Se3 is below 6 QLs, the surface state opens a gap at the Dirac Point (DP) due to the coupling between the top and bottom surfaces. Therefore, when 1QL Bi2Se3 is grown on a trivial insulator, the Dirac cone of the surface state of Bi2Se3 cannot survive. Then, a natural question is how about 1 QL Bi2Se3 film on another type of TI. On the other hand, when we just replace 1 nm thick surface layer of one TI by a different TI, what new property will come into being?

In this work, we epitaxially grow 1 QL Bi2Se3 on 19 QLs Bi2Te3 and form a 1 QL Bi2Se3/19 QLs Bi2Te3 heterostructure17. In situ ARPES results show that the surface state of the heterostructure 1 QL Bi2Se3/19 QLs Bi2Te3 is similar to the surface state of high electron doped Bi2Se3 film. Further ex situ measurements demonstrate that the transport properties of Bi2Se3/Bi2Te3 heterostructure, such as linear MR and WAL of our Bi2Se3/Bi2Te3 heterostructure behave totally different from that of pure Bi2Te3, but similar to pure Bi2Se3. The experiments show that the 1 QL Bi2Se3 top layer dominates the transport properties of the heterostructure and clearly demonstrates the effect of the surface state on the transport of a TI.

Results

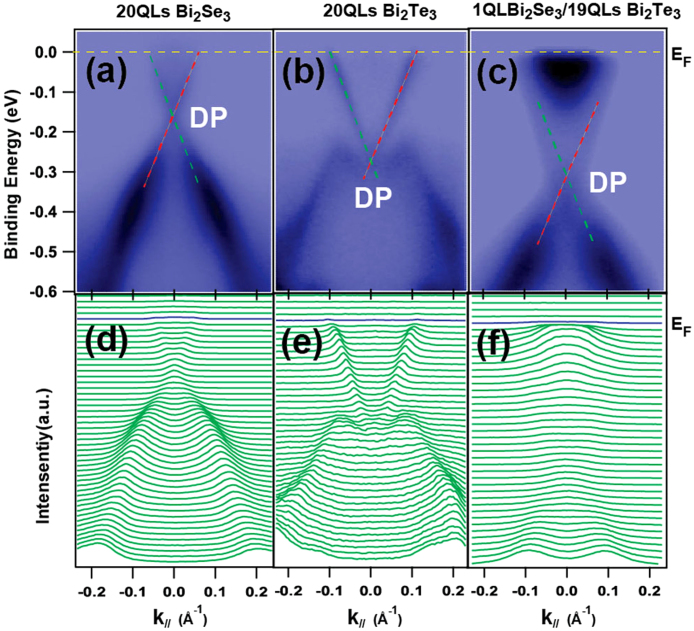
The TI thin films studied here are grown on the sapphire (0001) substrate by MBE17. Transport measurements are performed in a commercial physical property measurement system (PPMS-16T). The ARPES band dispersions and corresponding momentum distribution curves (MDCs) of 20 QLs Bi2Se3, 20 QLs Bi2Te3 and 1 QL Bi2Se3/19 QLs Bi2Te3 are shown in Fig. 1a to 1f, respectively. As shown in Fig. 1a and 1d, the DP of the 20 QLs Bi2Se3 lies in the bulk gap and is located at 0.17 eV below the Fermi level (EF). On the other hand, the ARPES band map of 20 QLs Bi2Te3 is different. The DP is buried in the bulk valance band and the EF lies near the bulk conduction band due to the n-type carriers caused by the Te vacancies (Fig. 1b and 1e). As reported before, when the thickness of Bi2Se3 is below 6 QLs, the surface state opens a gap at the DP due to the coupling between the top and bottom surfaces16. However, when 1 QL Bi2Se3 is epitaxially grown on 19 QLs Bi2Te3, a single gapless Dirac cone is observed in the bulk gap. The surface band dispersion near the DP, especially the position of DP is almost same with the surface state of electron doped Bi2Se3 films (Fig. 1c and 1f). The significant change in the surface band dispersion from that of Bi2Te3 to that of Bi2Se3, instead of co-existing of them, indicates that the 1 QL of Bi2Se3 basically covers the whole surface of Bi2Te3. The electron doping of 1QL Bi2Se3 is likely to be induced by the underneath Bi2Te3 which has higher electron doping level than that of Bi2Se3. Thus, the ultrathin 1 QL Bi2Se3 changes the surface state of the top surface of 19 QLs Bi2Te3 films and makes the 1 QL Bi2Se3/19 QLs Bi2Te3 heterostructure exhibit Bi2Se3 surface state characteristic. This observation is reasonable since surface states are localized near the surface region of a material, and therefore the surface band dispersion is mainly determined by the environment around surface.

Figure 1. ARPES results on 20 QLs Bi2Se3, 20 QLs Bi2Te3 and 1 QL Bi2Se3/19 QLs Bi2Te3 heterostructure thin films.

Figure 1

Open in a new tab

(a) 20 QLs Bi2Se3 (b) 20 QLs Bi2Te3 (c) 1 QL Bi2Se3/19 QLs Bi2Te3 heterostructure thin film measured along the K-Γ-Κ direction, the yellow line indicates the Fermi level, and the red and blue lines indicate the surface state. The lower figures (d) to (f) are the corresponding momentum distribution curves, the blue lines indicates the Fermi level.

1 QL Bi2Se3/19 QLs Bi2Te3 heterostructure film was examined by a FEI TITAN Cs-corrected STEM operating at 200 kV. Figure 2a shows a high angle annular dark field (HAADF) image of the heterostructure film with amorphous Te capping layer and sapphire substrate. Figure 2b and 2c show the atomic layer-by-layer HAADF images which manifest a high-quality single crystal nature of 1 QL Bi2Se3/19 QLs Bi2Te3 heterostructure film. According to the Z contrast, we infer the van der Waals gap indicated by the green dashed line is the interface between Bi2Se3 and Bi2Te3. Besides, the interfaces of Te capping layer/TI film and TI film/sapphire are clearly defined due to the different atomic structures, as marked by red and yellow dashed lines.

Figure 2. STEM-HAADF images of 1 QL Bi2Se3/19 QLs Bi2Te3 film on sapphire (0001).

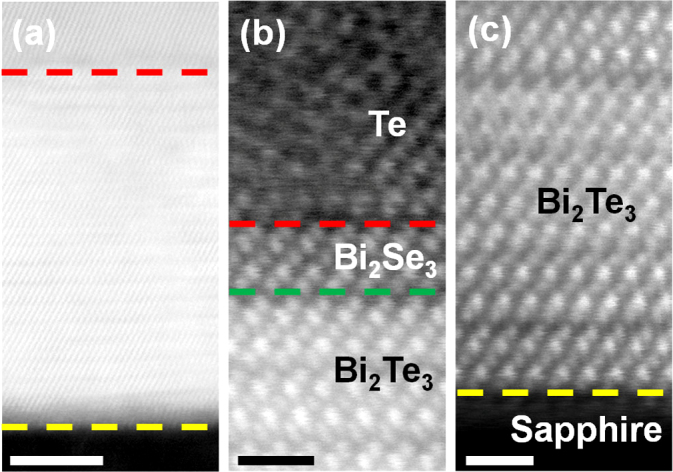
Figure 2

Open in a new tab

The dashed lines represent different interfaces (Red: Amorphous Te capping layer/TI film; Green: 1QL Bi2Se3/19 QLs Bi2Te3; Yellow: TI film/sapphire substrate). Scale bars are 5 nm (a), 1 nm (b), 1 nm (c).

Discussion

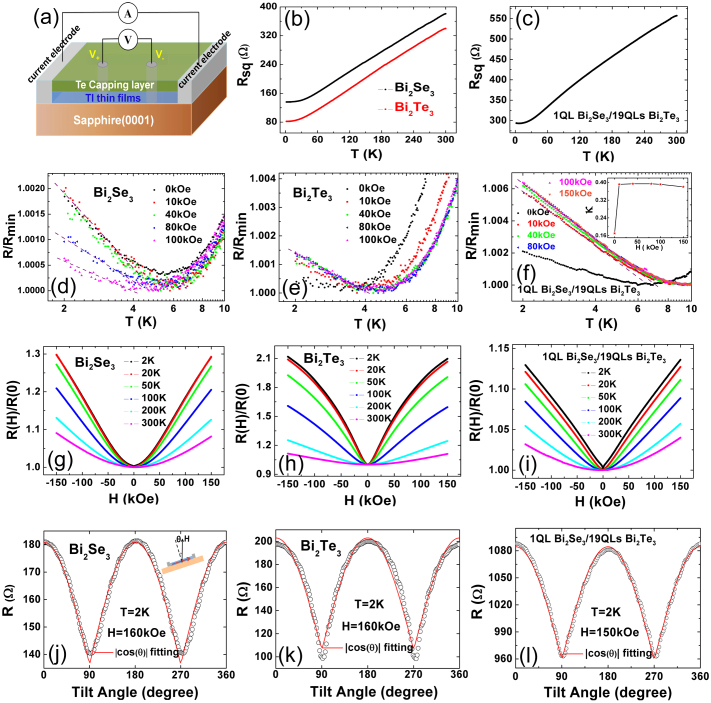
To further study the properties of 1 QL Bi2Se3/19 QLs Bi2Te3 heterostructure, we performed transport measurements on 20 QLs Bi2Se3, 20 QLs Bi2Te3 and 1QL Bi2Se3/19 QLs Bi2Te3 heterostructure films for comparison. Figure 3a is a schematic diagram of our transport measurement structure. Standard four probe method was used in all the measurements. We placed two indium current electrodes (I+ and I−) on both ends and across the entire width of the film strip with a size of 0.3 mm × 2 mm, so that the current can homogeneously go through the TI film in longitudinal direction. Then, two indium electrodes with the diameter of 0.3 mm were pressed on the film as voltage probes. In this paper, all the transport results are repeatable in different MBE-grown samples. Hall measurement results are shown in Fig. S1 in Supplementary Information. Figure 3b shows the temperature dependence of two dimensional (2D) sheet resistance (Rsq) for 20 QLs Bi2Se3 and 20 QLs Bi2Te3. In pure 20 QLs Bi2Se3 and 20 QLs Bi2Te3 films, with decreasing temperature (T), Rsq displays metallic behavior at high T region and becomes weakly insulating at low T regime. In Fig. 3c, the 1 QL Bi2Se3/19 QLs Bi2Te3 film shows the similar metallic behavior with the pure Bi2Te3 film at high T. However, it displays the stronger resistance upturn than the 20 QLs Bi2Te3 film at low T. Under a perpendicular magnetic field, the resistance upturn still exists for all three samples. It is reminiscent of the electron-electron interaction in TI films18. However, the slopes of the normalized resistance (R/Rmin) − lnT for 20 QLs Bi2Se3 and 20 QLs Bi2Te3 are different. For 20 QLs Bi2Se3 (Fig. 3d), the slope of R/Rmin − lnT shows obvious magnetic field-dependence. The dashed lines are eye-guides to show that R/Rmin increases logarithmically with T in low T regime. With increasing magnetic field, the resistance upturn is decreased and almost suppressed at 100 kOe. Nevertheless, as shown in Fig. 3e, the slope of R/Rmin − lnT of 20 QLs Bi2Te3 shows weak dependence of the external magnetic field and the resistance upturn is enhanced by the field. Figure 3f shows the normalized resistance versus T at different magnetic fields for 1 QL Bi2Se3/19 QLs Bi2Te3 heterostructure film. Compared with 20QLs Bi2Te3, the heterostructure shows more obvious upturn behavior which is nearly independent of magnetic field when the field is larger than 10 kOe. The slope of the resistance upturn is defined by κ = (πh/e2)dσxx/dlnΤ19. As shown in the inset, κ increases with increasing the magnetic field and becomes a constant when the magnetic field ranges from 10 kOe to 150 kOe. The electron-electron interaction causes a logarithmic increase of resistance while WAL induces a logarithmic decrease of resistance18,20. The two effects coexist and compete with each other. Thus, at zero field both WAL and electron-electron interaction cause lnT dependence which results a small κ. At higher magnetic field, the WAL contribution is suppressed and κ becomes a constant due to the strong electron-electron interaction (The complete data are shown in Fig. S2 in Supplementary Information).

Figure 3. Transport measurements on 20 QLs Bi2Se3, 20 QLs Bi2Te3 and 1 QL Bi2Se3/19 QLs Bi2Te3 heterosturcture films.

Figure 3

Open in a new tab

(a) Schematic structure of the TI films for transport measurements. The thickness is not to scale. (b) 2D sheet resistance (Rsq) vs temperature of 20 QLs Bi2Se3 and 20 QLs Bi2Te3 from room temperature to 2 K. (c) 2D sheet resistance (Rsq) as a function of temperature for 1 QL Bi2Se3/19 QLs Bi2Te3 heterostructure film. (d)–(f) The normalized resistance (R/Rmin) of 20 QLs Bi2Se3, 20 QLs Bi2Te3 and 1 QL Bi2Se3/19 QLs Bi2Te3 as a function of temperature at different magnetic field, indicate that a logarithmic increase with decreasing T (the dashed lines are guides to the eyes). In the upper inset of (f), the slope defined as κ = (πh/e2)dσxx/dlnΤ is shown as a function of magnetic field. (g)–(i) The normalized MR (R(H)/R(0)) vs magnetic field of 20 QLs Bi2Se3, 20 QLs Bi2Te3 and 1 QL Bi2Se3/19 QLs Bi2Te3 at different temperatures. (j) and (k) Resistance vs tilt angle of 20 QLs Bi2Se3 and 20 QLs Bi2Te3 in a fixed magnetic field of 160 kOe at T = 2 K. The inset shows the rotation configuration. The magnetic field is always perpendicular to the current when the sample is rotating. (l) Resistance vs tilt angle of 1 QL Bi2Se3/19 QLs Bi2Te3 in a fixed magnetic field of 150 kOe at T = 2 K. The function |cosθ| fitting is shown as solid red lines in (j)–(l).

Figure 3g and 3h show the normalized MR (R(H)/R(0)) of 20 QLs Bi2Se3 and 20 QLs Bi2Te3 thin films as a function of magnetic field perpendicular to thin films at different T. A linear and non-saturating MR is observed in the field up to 150 kOe for 20 QLs Bi2Se3 in Fig. 3g, which even maintains at the temperature above 50 K. On the other hand, as shown in Fig. 3h, the 20 QLs Bi2Te3 film displays a clearly nonlinear MR behavior and the value of normalized MR (R(H)/R(0)) is 2.18 at 2 K and 150 kOe, which is much larger than that of the 20 QLs Bi2Se3 film (1.3). The nonlinear MR is a typical behavior found in MBE-grown Bi2Te3 thin films21,22, though the linear MR behavior was ever observed in bulk Bi2Te323,24,25. The normalized MR of the 1 QL Bi2Se3/19 QLs Bi2Te3 film shows a linear, non-saturated and weakly temperature-dependent behavior across a wide range of magnetic field from 10 kOe to 150 kOe (Fig. 3i). According to Abrikosov's model, the linear and positive MR is expected to exist in the gapless semiconductor with a linear E-k dispersion26. In addition, the linear MR behavior of the 1 QL Bi2Se3/19 QLs Bi2Te3 film gradually decreased when the sample was tilted away from the perpendicular angle and eventually became nonlinear in the parallel magnetic field. (Fig. S3 in Supplementary Information) Hence, the linear MR probably comes from the 2D gapless TI surface state27,28,29.However, the MR of 20 QLs Bi2Te3 (Fig. 3h) shows an obviously nonlinear behavior while 20 QLs Bi2Se3 (Fig. 3g) displays a linear and positive MR. Therefore, it is believed that the 1 QL Bi2Se3 on the top of heterostructure plays a significant role in the transport property. The angular dependent MR of 20 QLs Bi2Se3 and 20 QLs Bi2Te3 thin films at 2 K and 160 kOe are shown in Fig. 3j and 3k. It is known that the 2D surface states of the TIs are only sensitive to the perpendicular component of the magnetic field Bcosθ, where θ is the angle between magnetic field and the normal direction of the thin films (Fig. 3j inset). For the 20 QLs Bi2Se3 film, the observed angular dependence of MR can be well fitted by a |cosθ| function. This suggests that the MR curve shows an obvious 2D response. Thus, the observed linear MR behavior from 20 QLs Bi2Se3 might be from the energy-momentum (E-k) linear relationship of 2D topological surface state27. Compared with Bi2Se3, the angular dependence of MR of 20 QLs Bi2Te3 film exhibits a little deviation with the |cosθ| fitting curve. Moreover, the curve of 1 QL Bi2Se3/19 QLs Bi2Te3 heterostructure film resistance versus the rotation angle at 2 K and 150 kOe matches well with the function of |cosθ| (Fig. 3l) too, implying the 2D nature of magneto-transport behavior.

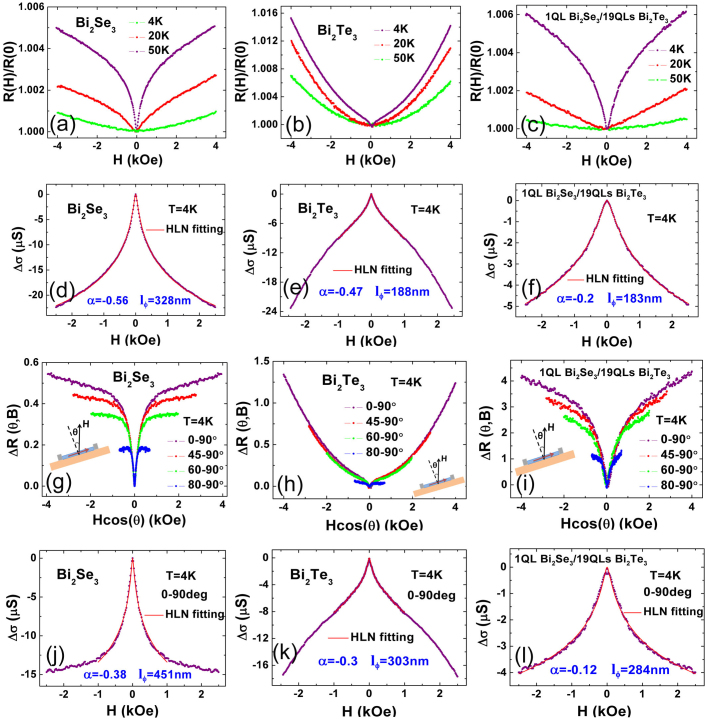
TI has spin-momentum locked surface states which lead to a π Berry phase suppressing the backscattering. The absence of backscattering results in the destructive interference between the two time reversal symmetry loops, which leads to the WAL effect and the perpendicular magnetic field can destroy this quantum interference. Figure 4 shows the WAL effect of our TI films in low field at different temperatures. With increasing T, the WAL effect becomes weaker and is suppressed at 50 K, as shown in Fig. 4a for 20 QLs Bi2Se3 and 4b for 20 QLs Bi2Te3. Compared with two WAL effects, we find that the 20 QLs Bi2Se3 film with a sharp cusp in low field while 20 QLs Bi2Te3 film displays smaller MR dip in lower field regime. In Fig. 4c, the 1 QL Bi2Se3/19 QLs Bi2Te3 film exhibits WAL effect in the low field too. The normalized MR shows a large cusp in the perpendicular field and the behavior is weakened with increasing temperature (Fig. 4c), which is more like that in pure 20 QLs Bi2Se3 (Fig. 4a) not 20 QLs Bi2Te3 (Fig. 4b).

Figure 4. WAL effect studied on 20 QLs Bi2Se3, 20 QLs Bi2Te3 and 1 QL Bi2Se3/19 QLs Bi2Te3 films.

Figure 4

Open in a new tab

(a)–(c) Normalized MR of 20 QLs Bi2Se3, 20 QLs Bi2Te3 and 1 QL Bi2Se3/19 QLs Bi2Te3 in the low field at different temperatures. (d)–(f) Fitted curves (solid red lines) with Eq. (1) are shown in 20 QLs Bi2Se3, 20 QLs Bi2Te3 and 1 QL Bi2Se3/19 QLs Bi2Te3 in perpendicular field at T = 4 K respectively. For the 20 QLs Bi2Se3 film and the 1 QL Bi2Se3/19 QLs Bi2Te3 film, the fitting range is from 2.5 kOe to −2.5 kOe. However, for the 20 QLs Bi2Te3 film, the WAL dip is small that the fitting range is from 1 kOe to −1 kOe. (g)–(i) MR as a function of the normal H component with the θ = 90° MR subtracted for 20 QLs Bi2Se3, 20 QLs Bi2Te3 and 1 QL Bi2Se3/19 QLs Bi2Se3 at θ equals to 0°, 45°, 60°, 80°. The inset shows the rotation configuration. (j)–(l) Violet symbols are the T = 4 K magneto conductance for the 20 QLs Bi2Se3 film (j), the 20 QLs Bi2Te3 film (k) and the 1 QL Bi2Se3/19 QLs Bi2Te3 film (l) after subtracting the 3D WAL effect. The solid red lines show the fitting results with Eq. (1). Compared with corresponding figure (d) to (f), all the phase coherence lengths of our TI films become larger after subtracting the 3D WAL effect.

According to the Hikami-Larkin-Nagaoka (HLN) theory30, the equation for 2D magnetoconductance (MC) is:

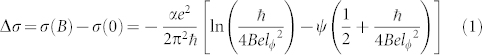graphic file with name srep03060-m1.jpg

Here Ψ(x) is the digamma function and lϕ is the phase coherence length. α is a coefficient reflecting the strength of the spin-orbital coupling and magnetic scattering. The value of α is 1, 0, −1/2 for the orthogonal, unitary and symplectic case, respectively. In TIs, the value of α indicates the type of the carriers. Considering the studies before18,31,32,33,34,35, the coefficient α changes from −0.4 to −1.1. α = −0.5 is owed to a single surface state and α = −1 indicates that both top and bottom surface states contribute the transport or top surface and bulk do the contribution. In our case, Δσ of 20 QLs Bi2Se3 film at 4 K in the perpendicular field fits the HLN equation quite well and yields α = −0.56 and lϕ = 328 nm (Fig. 4d). Fig. 4e shows the fitting results of 20 QLs Bi2Te3 film, whose values are α = −0.47 and lϕ = 188 nm. This suggests that one single surface channel dominates the WAL transport behavior. As shown by the red solid fitting curve in Fig. 4f, the fitting of 1 QL Bi2Se3/19 QLs Bi2Te3 film yields α = −0.2 and lϕ = 182 nm. Our extracted −α is smaller than 0.5, which is likely due to an enhanced electron-electron interaction of the carriers36,37. We have combined WAL and e-e interaction18 in the fitting (Fig. S4 in Supplementary Information). The value of −α equals to 0.32 is larger than that given by HLN fitting. In addition, the value of −α is still smaller than 0.5, which is indicative of increased localization effect. This could be due to a localization contribution from the bulk, for example, a bulk localization effect increased by the impurities at the interface. Besides, when the Fermi energy is close to the bulk band edge, the bulk would exhibit weak localization behavior (α > 0)38. Thus, the experimentally observed “weak antilocalization” in the 1 QL Bi2Se3/19 QLs Bi2Te3 film may also be a combined result from both the weak antilocalization of the surface channel and weak localization of the bulk channel38,39, which leads to a smaller −α. We stress that these are only suggestions and further studies will need to be done to clarify the mechanism.

Because the 3D magneto-transport for bulk electrons in TI films is independent of the tilt angle of the magnetic field and the bulk electrons dominate the transport in parallel field, we subtract the 3D WAL contribution measured in the parallel field θ = 90° from the MR measured in θ = 0°, 45°, 60°, 80°31 (Fig. 4g–4i). After removing the 3D bulk WAL effect, we can clearly observe the WAL effect caused by the 2D surface state of 20 QLs Bi2Se3, 20 QLs Bi2Te3 and 1 QL Bi2Se3/19 QLs Bi2Te3 at different angles in Fig. 4g, 4h and 4i respectively. For 20 QLs Bi2Se3, the curves show same cusp in low field (<1 kOe) which suggests that the observed WAL effect only relies on the perpendicular component of the magnetic field. In higher magnetic field, the curves deviate with each other, which is owing to the Zeeman effect40. Although similar WAL effect is also observed in 20 QLs Bi2Te3, the MR dip is apparent smaller than that of 20 QLs Bi2Se3. For the 1 QL Bi2Se3/19 QLs Bi2Te3 shown in Fig. 4i, it can be clearly observed that the surface state WAL behaves more like that in the 20 QLs Bi2Se3 film shown in Fig. 4g. After subtracting the 3D WAL effect, we can fit the MC behavior of TI films by equation (1). As shown in Fig. 4j, for 20 QLs Bi2Se3, α equals to −0.38 and lϕ is 451 nm. This is consistent with the value reported before32,33,41. Fig. 4k displays the fitting results of 20 QLs Bi2Te3 α = −0.3 and lϕ = 303 nm by subtracting the bulk effect, which is similar to previous report in Bi2Te3 films31. The phase coherence length becomes larger after subtracting the 3D effect, which indicates longer coherence length in surface transport channel. In Fig. 4l, we also fit the MC curve of 1 QL Bi2Se3/19 QLs Bi2Te3 from which the parallel component is removed. The value of α obtained from the fitting is −0.12 and the phase coherence length lϕ is 284 nm. Compared with the pure sample, the decrease of lϕ may also due to the enhanced electron-electron scattering rate in the heterostructure.

In summary, in situ ARPES experiments provide the direct evidence that the surface state of top surface of 1 QL Bi2Se3/19 QLs Bi2Te3 heterostructure is similar to the surface state of Bi2Se3. The high quality well-controlled epitaxial heterointerface was revealed by HRTEM. The transport properties of 20 QLs Bi2Se3, 20 QLs Bi2Te3 and 1 QL Bi2Se3/19 QLs Bi2Te3 films were studied. Both linear MR and WAL effect show that the heterostructure behaves more like Bi2Se3 even though there is only single Bi2Se3 layer grown on 19 QLs Bi2Te3 in the heterostructure. Therefore, the 1 QL Bi2Se3 in the heterostructure plays an important role in the transport property and increases the contribution of surface to some extent. Studying on this TI-TI heterostructure may provide a platform to artificially modulate the bulk and surface electronic structures of TIs respectively and pave a way for exploring potential applications in TI devices.

Methods

The MBE sample growth

The high quality 20 QLs Bi2Se3, 20 QLs Bi2Te3 and 1 QL Bi2Se3/19 QLs Bi2Te3 heterostructure films studied here were grown on sapphire (0001) in an ultra-high vacuum MBE-ARPES-STM combined system with a base pressure better than 2 × 10−10 mbar. Before sample growth, the sapphire substrates are first outgassed at 650°C for 90 min and then heated at 850°C for 30 min. High-purity Bi (99.9999%) and Se (99.999%) or Bi (99.9999%) and Te (99.9999%) are evaporated from standard Knudsen cells. To reduce Se vacancies in Bi2Se3 or Te vacancies in Bi2Te3, the growth is kept in Se or Te-rich condition with the substrate temperature at 180 ~ 220°C. When we grow the 1 QL Bi2Se3/19 QLs Bi2Te3 heterostructure film, 19 QLs Bi2Te3 films were firstly grown on sapphire (0001) and used as a substrate, and then 1QL Bi2Se3 film is deposited on thick 19 QLs Bi2Te3 films at the substrate temperature slightly lower (~20°C) than the growth temperature of thick 19 QLs Bi2Te3 films to reduce the possible intermixing of two different TI films.

ARPES measurements

The in situ ARPES measurements were carried out at ~150 K by using a Scienta SES2002 electron energy analyzer. A Helium discharge lamp with a photon energy of hν = 21.218 eV is used as the photon source. The energy and the angular resolutions were 15 meV and 0.2°, respectively. All the spectra shown in the paper are taken along the Γ-Κ direction. To avoid sample charging during ARPES measurements due to the insulating sapphire (0001) substrate, a 300-nm-thick titanium film is deposited at both ends of the substrate, which is connected to the sample holder. Once a continuous film is formed, the TI films are grounded through these contacts.

Author Contributions

J.W. and K.H. conceived and designed the study. Y.Z., Y.S., H.W., Y.X. and J.W. carried on transport measurement. C.C. did MBE growth and ARPES experiment. K.H., X.M. and Q.X. supervised the MBE growth and ARPES experiment. Y.J. and Y.W. made TEM study. Y.Z., C.C., A.D., Y.W. and J.W. analyzed the data. Y.Z. and J.W. wrote the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep03060-s1.pdf (476KB, pdf)

Acknowledgments

We acknowledge Moses H. W. Chan, Jainendra Jain, Nitin Samarth, Haizhou Lu, Yongqing Li, Zhong Fang, Haiwen Liu, Xinzheng Li, Junren Shi, Xincheng Xie, Ryuichi Shindou and Qingfeng Sun for fruitful discussions. This work was financially supported by National Basic Research Program of China (Grant Nos. 2013CB934600 & 2012CB921300), the National Natural Science Foundation of China (Nos. 11222434 & 11174007), and China Postdoctoral Science Foundation (No. 2011M500180 & No. 2012T50012).

References

  1. Hasan M. Z. & Kane C. L. Colloquium: Topological Insulators. Rev. Mod. Phys. 82, 3045–3067 (2010). [Google Scholar]
  2. Qi X. L. & Zhang S. C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011). [Google Scholar]
  3. Chen Y. L. et al. Experimental realization of a Three-Dimensional topological insulator, Bi2Te3. Science 325, 178–181 (2009). [DOI] [PubMed] [Google Scholar]
  4. Xia Y. et al. Observation of a large-gap topological insulator class with a single dirac cone on the surface. Nat. Phys. 5, 398–402 (2009). [Google Scholar]
  5. Fu L. & Kane C. L. Mele. Superconducting proximity effect and Majorana Fermions at the surface of a Topological Insulator. Phys. Rev. Lett. 100, 096407 (2008). [DOI] [PubMed] [Google Scholar]
  6. Qi X. L., Hughes T. L. & Zhang S. C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B. 78, 195424 (2008). [Google Scholar]
  7. Qi X. L., Li R. D. & Zhang S. C. Inducing a magnetic monopole with topological surface states. Science 323, 1184–1187 (2009). [DOI] [PubMed] [Google Scholar]
  8. Yu R. et al. Quantized anomalous hall effect in magnetic topological insulators. Science 329, 61–64 (2010). [DOI] [PubMed] [Google Scholar]
  9. Chang C. Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013). [DOI] [PubMed] [Google Scholar]
  10. Moore J. E. The birth of topological insulators. Nature. 464, 194–198 (2010). [DOI] [PubMed] [Google Scholar]
  11. Klitzing K. V., Dorda G. & Pepper M. New method for high-accuracy determination of the fine-structure constant based on quantized hall resistance. Phys. Rev. Lett. 45, 494–497 (1980). [Google Scholar]
  12. Tsui D. C., Stormer H. L. & Gossard A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982). [Google Scholar]
  13. Zhang Q. F. et al. Exotic topological insulator states and topological phase transitions in Sb2Se3-Bi2Se3 heterostructures. Acs Nano. 6, 2345–2352 (2012). [DOI] [PubMed] [Google Scholar]
  14. Hirahara T. et al. Atomic and electronic structure of ultrathin Bi(111) films grown on Bi2Te3 (111) substrates: evidence for a strain-induced topological phase transition. Phys. Rev. Lett. 109, 227401 (2012). [DOI] [PubMed] [Google Scholar]
  15. Valla T. et al. Topological semimetal in a Bi-Bi2Se3 infinitely adaptive superlattice phase. Phys. Rev. B. 86, 241101(R) (2012). [Google Scholar]
  16. Zhang Y. et al. Crossover of the three-dimensional topological insulator Bi2Se3 to the two-dimensional limit. Nat. Phys. 6, 584–588 (2010). [Google Scholar]
  17. Chang C. Z. et al. Growth of quantum well films of topological insulator Bi2Se3 on insulating substrate. SPIN 1, 21–25 (2011) [Google Scholar]
  18. Wang J. et al. Evidence for electron-electron interaction in topological insulator thin films. Phys. Rev. B. 83, 245438 (2011). [Google Scholar]
  19. Chen J. et al. Tunable surface conductivity in Bi2Se3 revealed in diffusive electron transport. Phys. Rev. B. 83, 241304(R) (2011). [Google Scholar]
  20. Ostrovsky P. M., Gornyi I. V. & Mirlin A. D. Interaction-Induced Criticality in Z2 Topological Insulators. Phys. Rev. Lett. 105, 036803 (2010). [DOI] [PubMed] [Google Scholar]
  21. Roy A. et al. Two-dimensional weak anti-localization in Bi2Te3 thin film grown on Si(111)-(7 × 7) surface by molecular beam epitaxy. Appl. Phys. Lett. 102, 163118 (2013). [Google Scholar]
  22. Yu X. X. et al. Separation of top and bottom surface conduction in Bi2Te3 thin films. Nanotechnology 24, 015705 (2013). [DOI] [PubMed] [Google Scholar]
  23. Qu D. X. et al. Quantum Oscillations and Hall Anomaly of Surface States in the Topological Insulator Bi2Te3. Science 329, 821–824 (2010). [DOI] [PubMed] [Google Scholar]
  24. Wang X., Du Y., Dou S. & Zhang C. Room Temperature Giant and Linear Magnetoresistance in Topological Insulator Bi2Te3 Nanosheets. Phys. Rev. Lett. 108, 266806 (2012). [DOI] [PubMed] [Google Scholar]
  25. Zhang S. X. et al. Magneto-resistance up to 60 Tesla in topological insulator Bi2Te3 thin films. Appl. Phys. Lett. 101, 202403 (2012). [Google Scholar]
  26. Abrikosov A. A. Quantum magnetoresistance. Phys. Rev. B. 58, 2788–2794 (1988). [Google Scholar]
  27. Tang H. et al. Two-dimensional transport-induced linear magneto-resistance in topological insulator Bi2Se3 nanoribbons. Acs Nano. 5, 7510–7516 (2011). [DOI] [PubMed] [Google Scholar]
  28. He H. T. et al. High-field linear magneto-resistance in topological insulator Bi2Se3 thin films. Appl. Phys. Lett. 100, 032105 (2012). [Google Scholar]
  29. Wang C. M. & Lei X. L. Linear magnetoresistance on the topological surface. Phys. Rev. B. 86, 035442 (2012). [Google Scholar]
  30. Hikami S., Larkin A. I. & Nagaoka Y. Spin-orbit interaction and magnetoresistance in the two dimensional random system. Prog. Theor. Phys. 63, 707–710 (1980). [Google Scholar]
  31. He H. T. et al. Impurity effect on weak antilocalization in the topological insulator Bi2Te3. Phys. Rev. Lett. 106, 166805 (2011). [DOI] [PubMed] [Google Scholar]
  32. Checkelsky J. G. et al. Bulk Band Gap and Surface State Conduction Observed in Voltage-Tuned Crystals of the Topological Insulator Bi2Se3. Phys. Rev. Lett. 103, 196801 (2011). [DOI] [PubMed] [Google Scholar]
  33. Chen J. et al. Gate-Voltage Control of Chemical Potential and Weak Antilocalization in Bi2Se3. Phys. Rev. Lett. 105, 176602 (2010). [DOI] [PubMed] [Google Scholar]
  34. Bansal N. et al. Thickness-independent transport channels in topological insulator Bi2Se3 thin films. Phys. Rev. Lett. 109, 116804 (2012). [DOI] [PubMed] [Google Scholar]
  35. Bao L. H. et al. Weak anti-localization and quantum oscillations of surface states in topological insulator Bi2Se2Te. Sci. Rep. 2, 726 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Taskin A. A. et al. Manifestation of Topological Protection in Transport Properties of Epitaxial Bi2Se3 Thin Films. Phys. Rev. Lett. 109, 066803 (2012). [DOI] [PubMed] [Google Scholar]
  37. Chiu S. P. & Lin J. J. Weak antilocalization in topological insulator Bi2Te3 microflakes. Phys. Rev. B. 87, 035112 (2013). [Google Scholar]
  38. Lu H. Z. & Shen S. Q. Weak localization of bulk channels in topological insulator thin films. Phys. Rev. B. 84, 125138 (2011). [Google Scholar]
  39. Garate I. & Glazman L. Weak localization and antilocalization in topological insulator thin films with coherent bulk-surface coupling. Phys. Rev. B. 86, 035422 (2012). [Google Scholar]
  40. Meijer F. E. et al. Universal spin-induced time reversal symmetry breaking in two-dimensional electron gases with Rashba spin-orbit interaction. Phys. Rev. Lett. 94, 186805 (2005). [DOI] [PubMed] [Google Scholar]
  41. Matsuo S. et al. Weak antilocalization and conductance fluctuation in a submicrometer-sized wire of epitaxial Bi2Se3. Phys. Rev. B. 85, 075440 (2012). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep03060-s1.pdf (476KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES